Газовые смеси метод В.Н.Диденко_. Газовые смеси
 Скачать 1.16 Mb.
|
|
2.1.1. Частные случаи смешения газов при W=Const Рассмотрим несколько частных случаев формул (2.1.6), (2.1.7), (2.1.10) и (2.1.11). Пусть смешиваются газы, у которых зависимостью показателя адиабаты Кi от температуры можно пренебречь. (В действительности К убывает с ростом температуры, т. к. 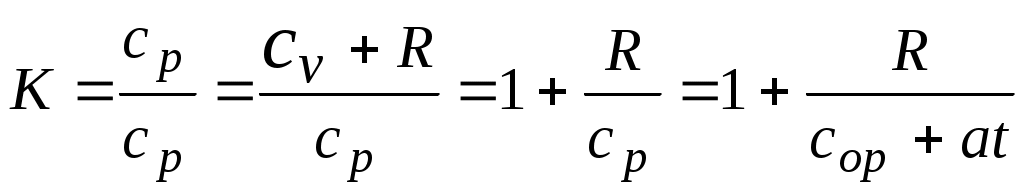 где со р ,а – эмперические положительные коэффициенты. Для технических расчетов в диапазоне от 0 до 20000С можно пользоваться следующими формулами: а) для двухатомных газов К  1,40 - 0,5010-4 t;б) для продуктов сгорания К 1,35 - 0,5510-4 t.Из этих формул видно, что влияние температуры на показатель адиабаты К становится заметным лишь при температурах, порядка сотен градусов по шкале Цельсия.) Т. о., если допустить, что 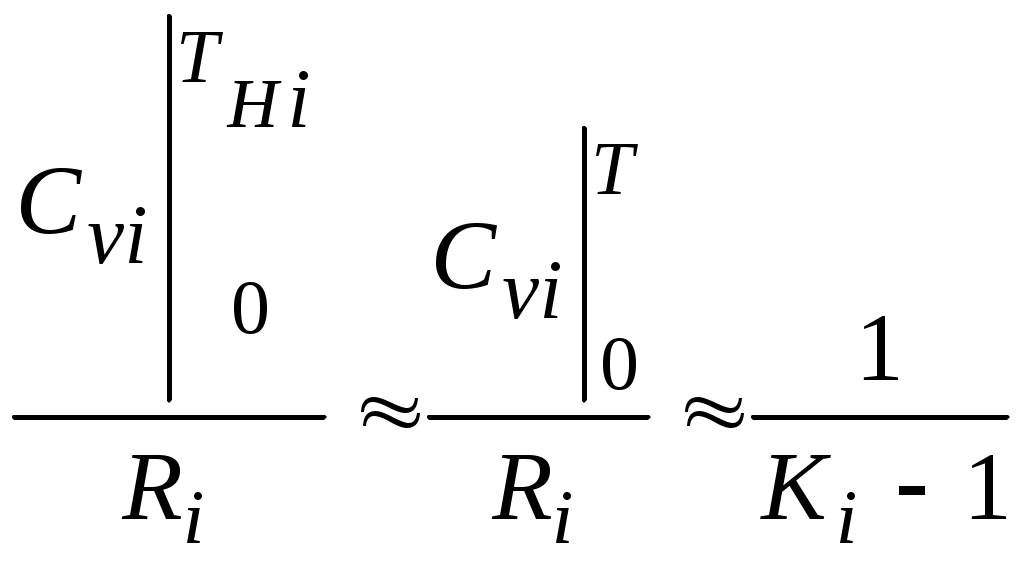 ,то формула (2.1.6) примет следующий вид: 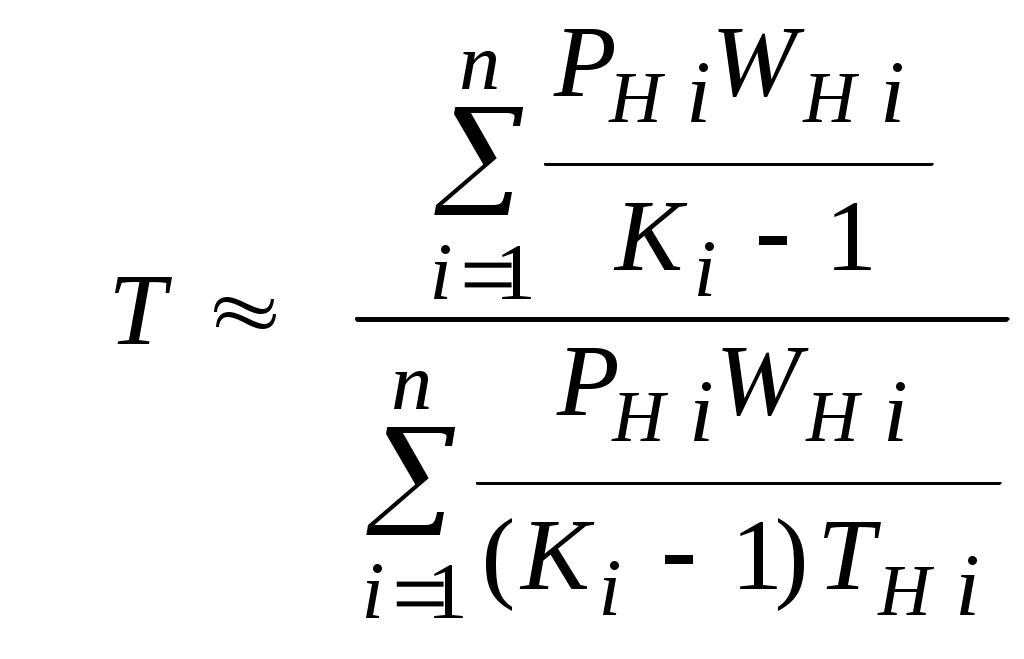 (2.1.12)Формулу (2.1.12) можно использовать в качестве первого приближения для формул (2.1.6), (2.1.7), (2.1.10) и (2.1.11) Пусть смешиваются газы, у которых мольные изохорные теплоемкости равны и зависимостью этих теплоемкостей от температуры можно пренебречь, т. е.:   .Тогда уравнение (2.1.7) принимает очень простой вид: 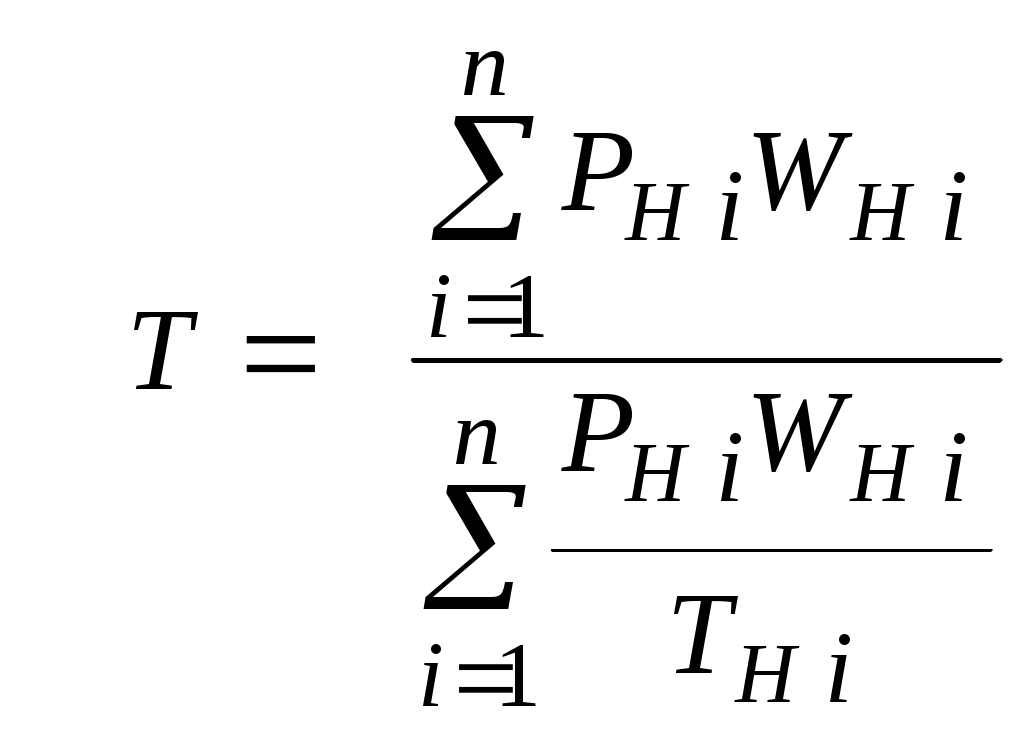 (2.1.13)Если у газов равны между собой мольные изохорные теплоемкости, то в соответствии с уравнением Майера  ,должны быть равны между собой и мольные изобарные теплоемкости, а, следовательно, равны и показатели адиабаты, т. е.  .При этом условии уравнение (2.1.12) превращается в (2.1.13). 2.1.2. Давление после смешения газов при W=Const Давление, устанавливающееся после смешения газов, можно определить либо по формулам параграфа 1.4.2, либо из условия: РсмWсм = mсмRсмТ = mсмТ  .Откуда  или 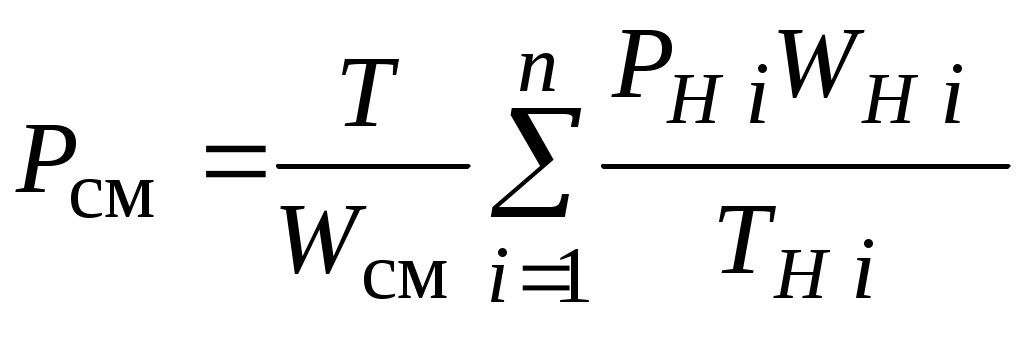 (2.1.14)Для частного случая 2 давление смеси получим путем подстановки формулы (2.1.13) в (2.1.14), откуда  Смешение газовых потоков Температура смеси газовых потоков Пусть в проточной смесительной камере смешиваются nпотоков, массовые расходы которых равны GH1 , GH 2,…, GHn, объемные расходы - QH1, QH 2,… , QHn, а начальные температуры и давления - ТH 1, ТH 2,…, ТHn и РH 1, РH 2,…, РHn. Давление газов в смесителе Pсм является величиной задаваемой из каких-либо соображений и устанавливаемой за счет дросселерования газовых потоков с помощью регулирующей арматуры (задвижек, клапанов и т. п.), установленной перед входом в смеситель. Это давление не должно быть больше минимального из PHi, т. е. должно выполняться условие: Pсм  (PH i) min .Здесь: i = 1, 2, 3, …, n. Если газы при смешении не совершают технической работы, то, полагая процесс смешения адиабатным, т. е. идущим без теплообмена с окружающей средой, и пренебрегая кинетической энергии потока, первое начало термодинамики для газового потока можно записать в следующем виде:  Здесь: iсм – удельная энтальпия смеси газов; iHi - удельная энтальпия i-го газа с начальной температурой ТHi; Gсм – массовый расход потока после смесителя.  Но, как известно, di = CpdT, откуда:  и  Здесь:  - средняя в диапазоне 0 -Т0К массовая изобарная теплоемкость смеси газов;  - средняя в диапазоне 0 -ТHi массовая изобарная теплоемкость i-го газа. Дальнейший вывод формул для температуры смеси потоков газа аналогичен выводу для случая смешения газов при сохранении постоянного объема, но вместо изохорной теплоемкости Сv в уравнения подставляется изобарная Сp. Тогда по аналогии с формулами предыдущего параграфа 2.1 можно сразу записать: 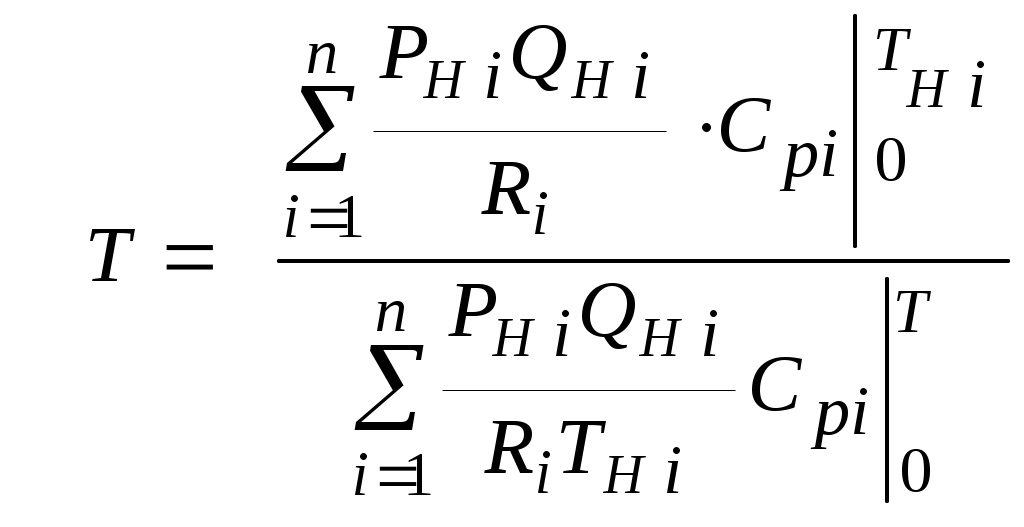 , (2.2.1)или 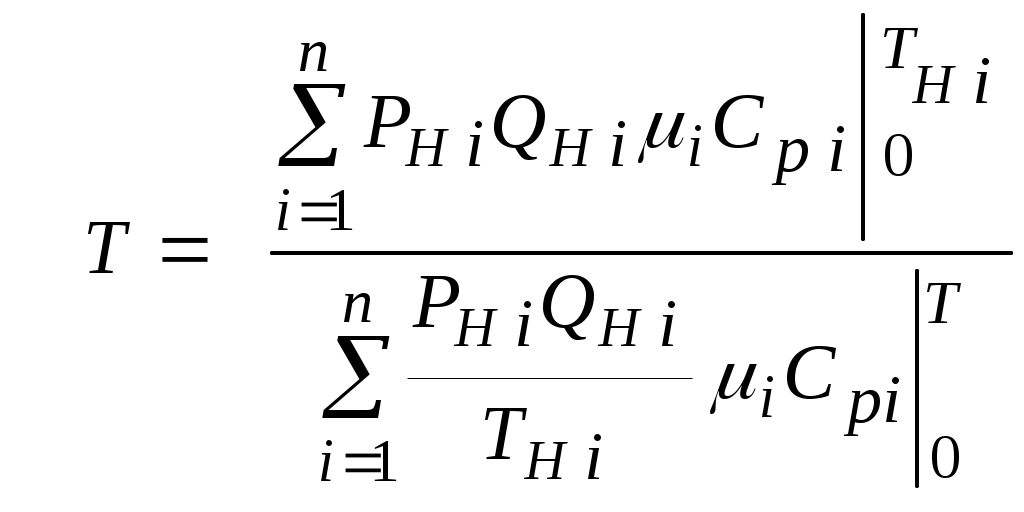 , (2.2.2)В тех случаях, когда эмпирическая зависимость теплоемкости от температуры дается для температуры в градусах Цельсия, формулы (2.2.1) и (2.2.2) приобретают соответственно следующий вид: 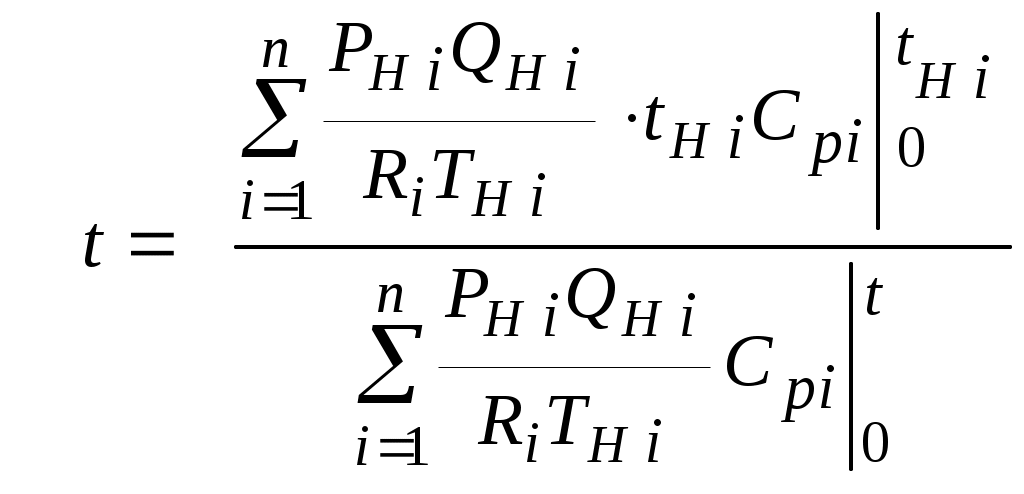 (2.2.5)или 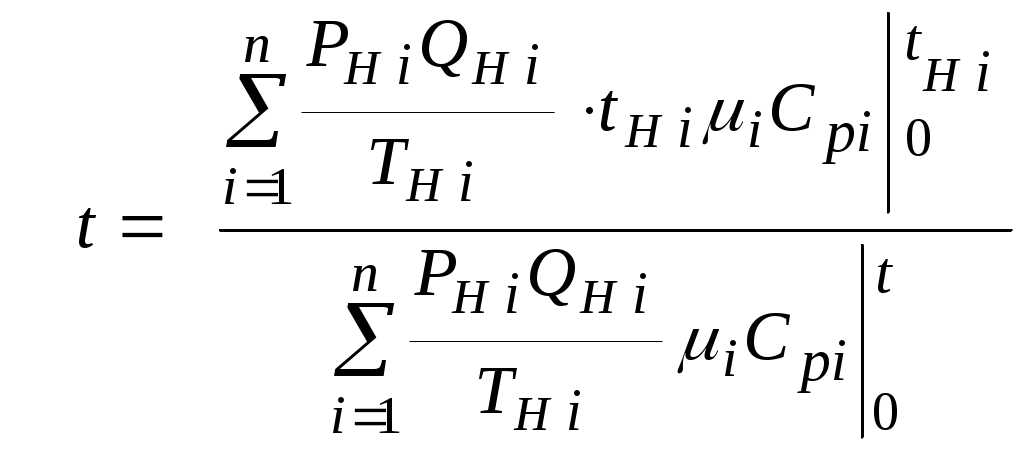 (2.2.6)Значения температуры смеси в формулах (2.2.1), (2.2.2), (2.2.5), (2.2.6) определяются методом последовательных приближений. Объемный расход смеси газовых потоков В отличие от массового расхода Gсм величина объемного расхода смеси Qсм в общем случае не равна сумме объемных расходов компонентов и определяется из уравнения состояния идеального газа, записанного для единицы времени:   .Т. к..  , то (2.2.3)Если выразить Gi через параметры начального состояния i-го потока 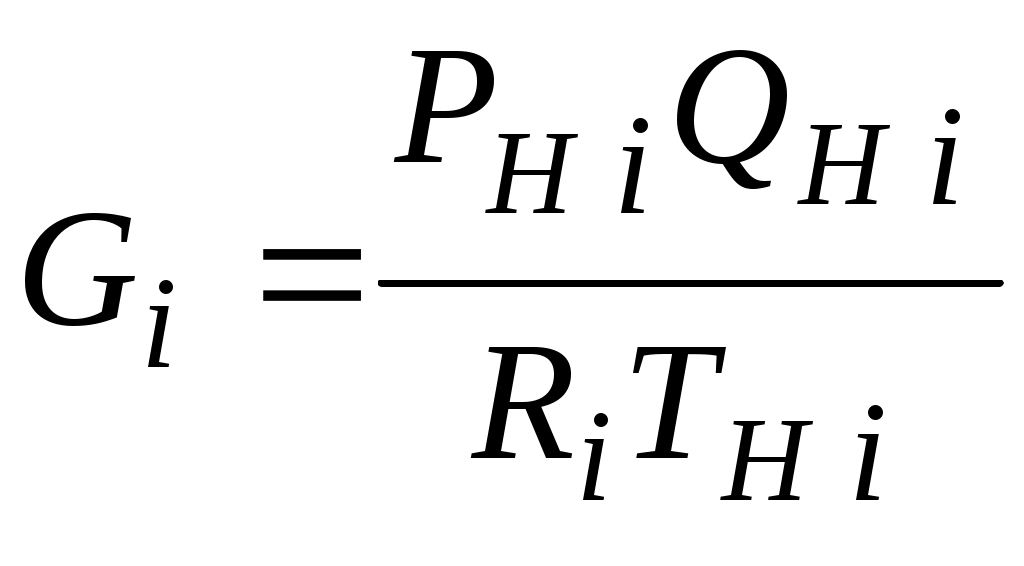 ,то получим еще одну формулу для объемного расхода смеси: 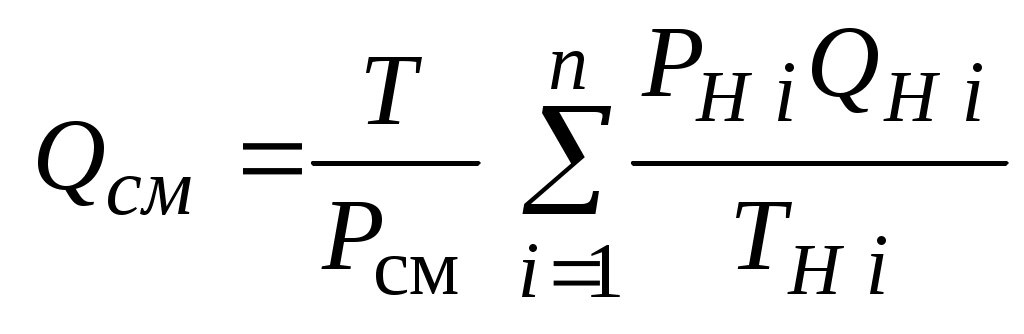 (2.2.4)2.2.3. Частные случаи смешения газовых потоков Рассмотрим несколько частных случаев формул (2.2.1) и (2.2.2). Если приближенно принять, что 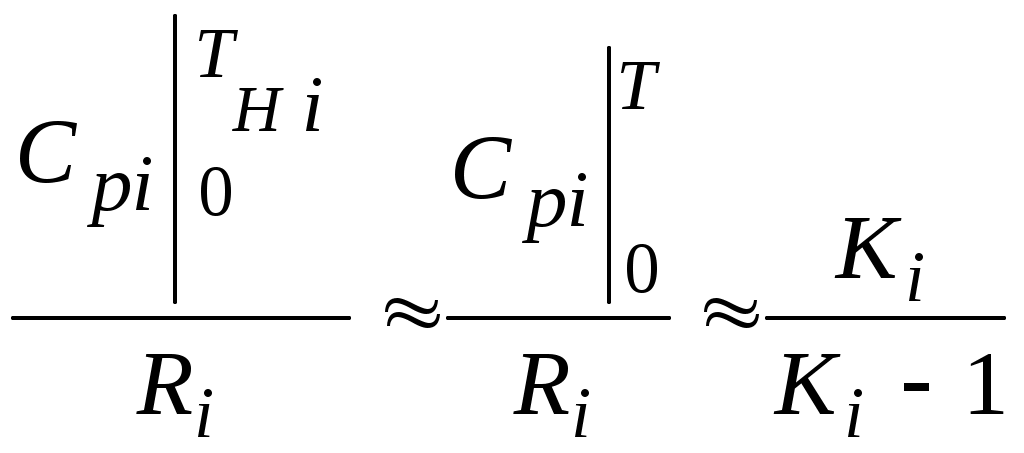 ,т. е. пренебречь зависимостью показателей адиабаты Кi от температуры, то формула (2.2.1) запишется в следующем виде: 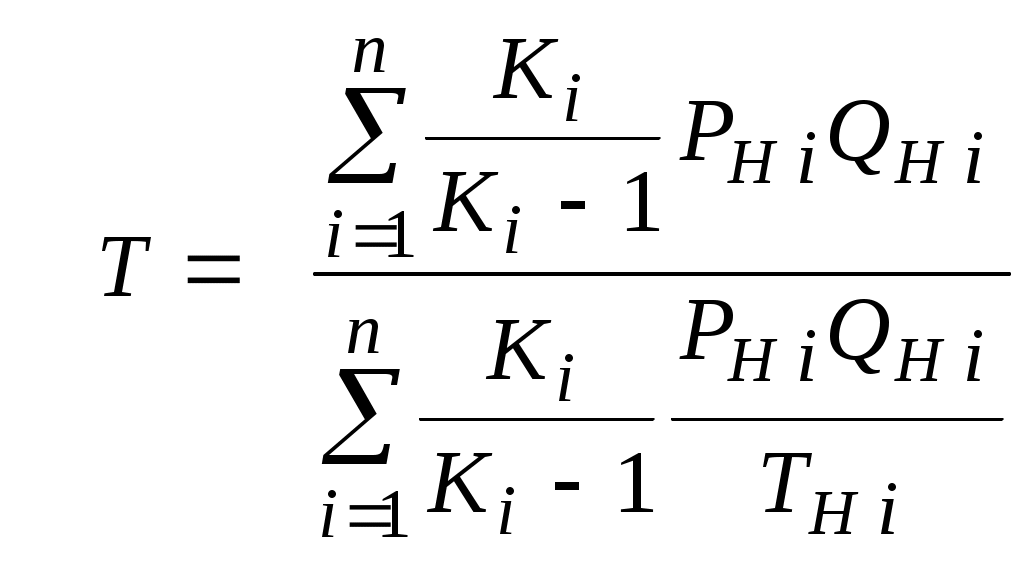 (2.2.7)Эта формула может быть использована в качестве первого приближения для температуры смеси Т в формулах (2.2.1) и (2.2.2). Если все газы, образующие смесь, имеют одинаковые и постоянные (или близкие) во всем диапазоне температур мольные теплоемкости, т.е.   ,то формула (2.2.2) упрощается: 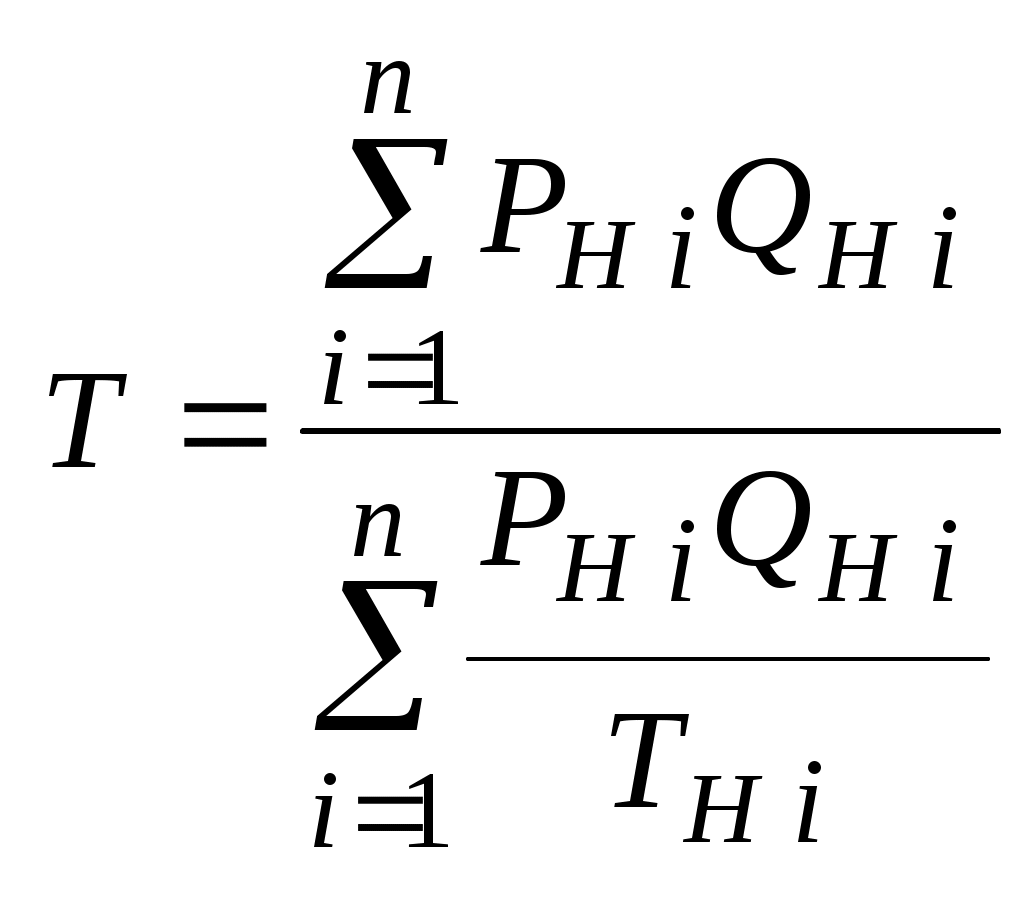 (2.2.8)Если помимо одинаковых мольных теплоемкостей (как в частном случае 2) все газы имеют одинаковое начальное давление, т. е.  ,то формула (2.2.8) принимает следующий вид: 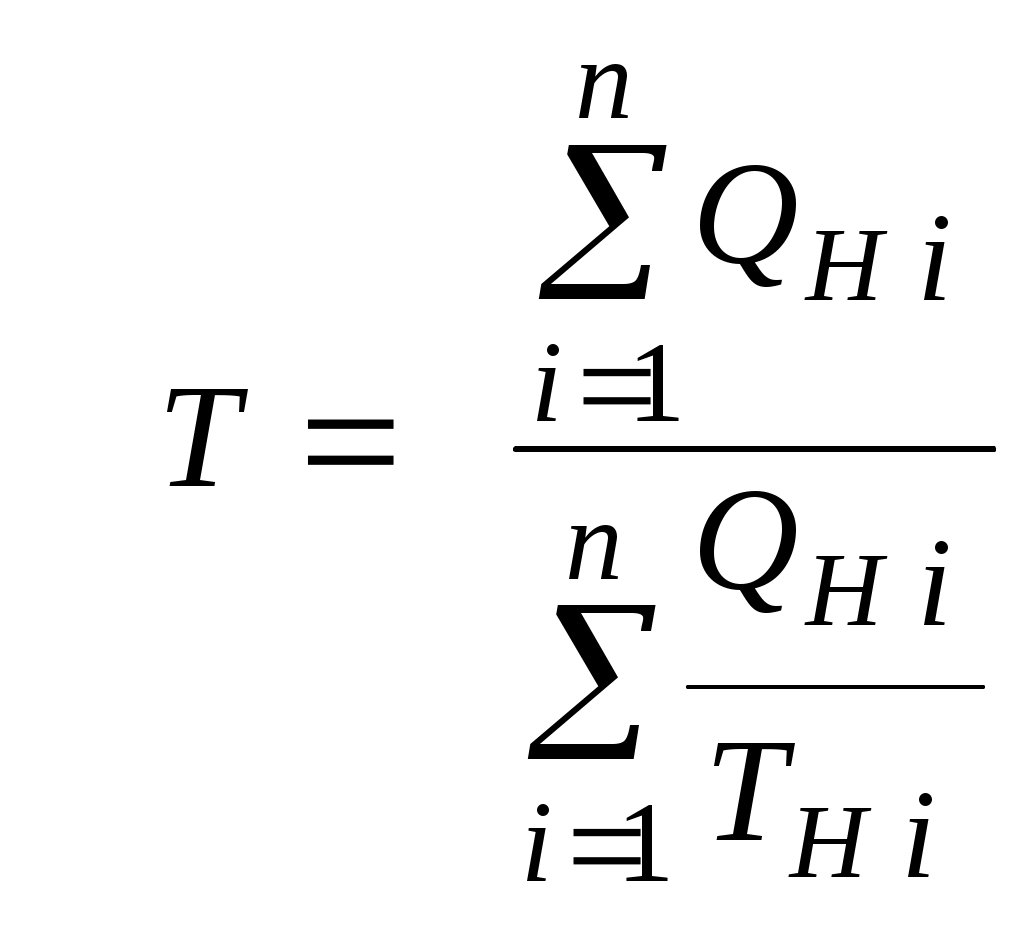 (2.2.9)Формула 2.2.4 для случая одинаковых начальных давлений ( 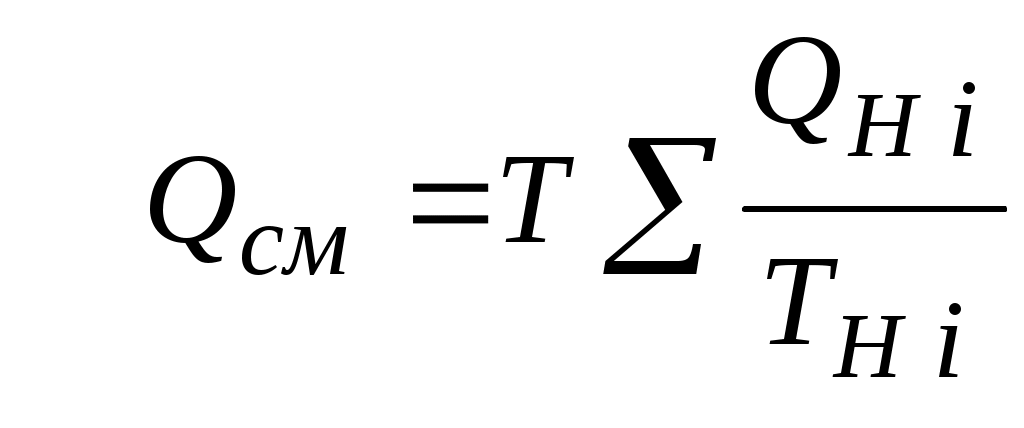) запишется как: (2.2.10)Если, кроме PHiравны между собой еще и начальные температуры ТHi, то  (2.2.11)Литература. 1. Берд Р., Стьюарт В., Лайтфут Е. Явления переноса. Перевод с англ. – М.: Химия; 1974. - 2. Розловский А. И. Научные основы техники взрывобезопасности при работе с горючими газами и парами. М.: Химия; 1972. – 90 с. 3. Гиршфельдер Дж., Кертисс Ч., Берд Р. Молекулярная теория газов и жидкостей. – М.: ИИЛ; 1961. – 929 с. 4. Рид Д., Праусниц, Шервуд. Свойства газов и жидкости. – М.: Мир; 1984. – с. 5. Стаскевич Н. Л., Северинец Г. Н., Вигдорчик Д. Я. Справочник по газоснабжению и использованию газа. – Л.: Недра, 1990. – 762 с. Ижевский государственный технический университет Институт городского хозяйства Диденко В. Н. Газовые смеси. Смешение газов. Ижевск 2002 Газовые смеси. Смешение газов. Методическое пособие к дисциплинам «Термодинамика», «Теплотехника», «Газоснабжение», «Химическая термодинамика и энергетика топлива», «Физико-химические основы горения топлива» специальностей 29.07.00 «Теплогазоснабжение и вентиляция» и 29.08.00 «Водоснабжение и водоотведение» Составитель: проф., д. т. н. Диденко Валерий Николаевич Методическое пособие содержит систематизированные теоретические сведения, необходимые для осознанного и грамотного использования зависимостей, приводимых в технической литературе, для расчета термодинамических параметров и функций, а также теплофизических характеристик газовых смесей. Целью методического пособия является устранение существующего пробела в доказательной части содержания разделов «газовые смеси» современных учебников и справочников по термодинамике, теплотехнике и газоснабжению. Методическое пособие предназначено для студентов технических специальностей, инженеров-теплотехников и аспирантов. © Ижевский государственный технический университет, 2002 © Институт городского хозяйства, 2002 © Диденко Валерий Николаевич, 2002. Содержание Газовые смеси 1.1. Основные признаки газовых смесей 1.2. Основные понятия и определения газовых смесей 1.3. Способы задания состава смеси реальных газов 1.4. Смеси идеальных газов 1.4.1.Характеристические функции и функции состояния газовых смесей 1.4.1.1. Удельные значения функций и параметров смеси газов 1.4.1.2. Мольные значения функций и параметров смеси газов 1.4.2. Парциальное давление 1.4.3. Парциальный объем 1.4.4. Задание состава смеси идеальных газов объемными долями 1.4.5.Формулы пересчета для различных способов задания состава газовых смесей 1.4.6.Кажущаяся молекулярная масса смеси газов 1.4.7.Газовая постоянная смеси газов 1.4.8.Плотность смеси газов 1.4.9.Энтропия смеси идеальных газов 1.4.10.Теплоемкость газовой смеси 1.4.11.Коэффициент теплопроводности, коэффициент динамической вязкости газовой смеси 1.4.11.1.Бинарные смеси 1.4.11.2.Многокомпонентные смеси 2. Смешение газов 2.1. Смешение при W=Const 2.1.1. Частные случаи смешения газов при W=Const 2.1.2. Давление после смешения газов при W=Const 2.2. Смешение газовых потоков 2.2.1. Температура смеси газовых потоков 2.2.2. Объемный расход смеси газовых потоков 2.2.3. Частные случаи смешения газовых потоков |