Газовые смеси метод В.Н.Диденко_. Газовые смеси

• Название: Газовые смеси
• Дата: 11.11.2022
• Размер: 1.16 Mb.
• Имя файла: Газовые смеси метод В.Н.Диденко_.doc
• Тип: Документы; #782314
• страница: 2 из 3

1.4.8. Плотность смеси газов

Плотность однородного газа, заменяющего смесь, называется плотностью смеси:

В справочниках обычно приводится без объяснений следующая формула для плотности смеси:

В то же время в технической литературе встречаются формулы вида

С вычислением плотности смеси через плотности компонентов связано наибольшее число студенческих ошибок. Дело в том, что значение плотности -го компонента можно формально получить из двух формул:

и
Т. к. , то значения и заметно отличаются друг от друга.

Проясним вопрос с вычислением плотности смеси.

По определению и , тогда .
Но и
Т. о. в последней формуле плотность i-го газа вычисляется как плотность этого газа, находящегося в количестве килограммов в объеме (парциальном объеме) при давлении смеси и температуре смеси .

Такое толкование плотности компонентов смеси используется, в частности, при расчете объемов продуктов сгорания топлива.

Если плотность i-го газа в смеси вычислять через его парциальное давление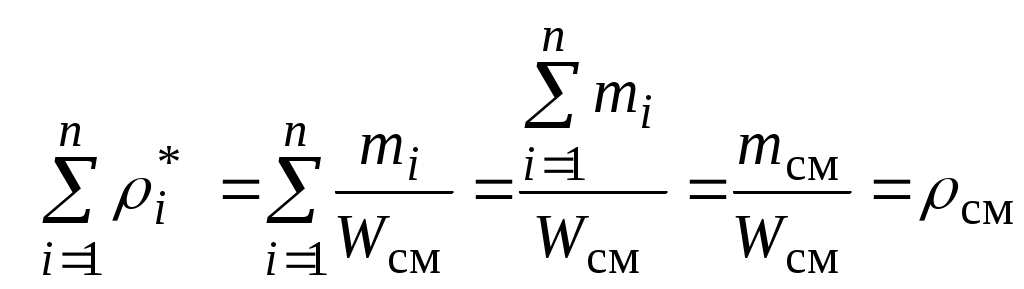
, то
Т. о. в этой формуле плотность i-го газа - это плотность газа массой , находящегося в объеме (объем смеси) при его парциальном давлении и температуре (температуре смеси).

Такое толкование плотности компонентов смеси, в частности, используется при определении абсолютной и относительной влажности воздуха.

1.4.9. Энтропия смеси идеальных газов
Как указано в параграфе 1.4.1., энтропия 1 кг - компонентной смеси идеальных газов (удельная энтропия смеси) S_см , Дж / (К · кг), определяется по следующей формуле:
,
где: - энтропия 1 кг i-го газа.

Из курса общей термодинамики известно:
,
где: - массовая изобарная теплоемкость i-го газа.

Окончательно удельная энтропия -компонентной смеси может быть вычислена по следующей формуле:



1.4.10. Теплоемкость газовой смеси
По определению, теплоемкость - это количество теплоты, которое необходимо для изменения температуры единицы количества вещества

( ) на один градус.

Т. к. температура всех газов в смеси одинакова, то теплоемкость смеси, складывается из теплоемкостей всех компонентов, взятых в долях, соответствующих способу задания смеси:
- массовая (удельная) теплоемкость, Дж / (кг·К);
- мольная теплоемкость, Дж / (кмоль·К);
- объемная теплоемкость, Дж / (м³·К).
где: - массовая, мольная и объемная теплоемкости i-го компонента.

1.4.11. Коэффициент теплопроводности,

коэффициент динамической вязкости

газовой смеси.
1.4.11.1. Бинарные смеси

• 
  В работе , для бинарных газовых смесей (смесей двух газов) рекомендован универсальный метод расчета коэффициентов теплопроводности и динамической вязкости.
  

- Коэффициент теплопроводности смеси: λ _см , Вт / (м · К):
,
где: и - коэффициенты теплопроводности первого и второго

компонентов бинарной смеси, взятые при температуре смеси.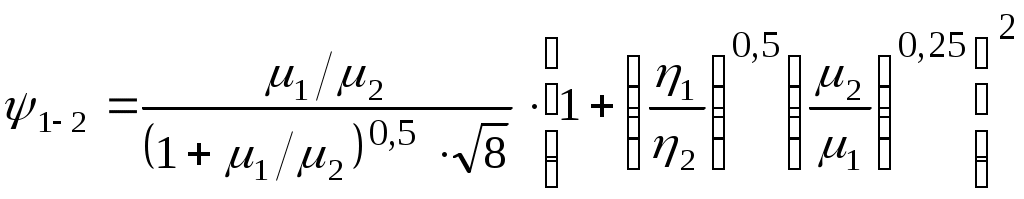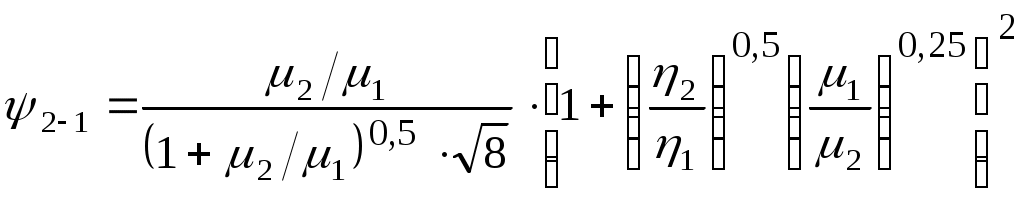

- поправочные коэффициенты.




Здесь: - коэффициенты динамической вязкости компонентов

- молекулярные массы компонентов.

1. 
   Коэффициент динамической вязкости смеси η_см, Па · С:
   

Средняя погрешность вычисления по этому методу составляет примерно 4%, а погрешность вычисления - в среднем 2%.

• 
  Бинарные смеси являются наиболее исследованными. Опыт показывает следующее :
  

1. 
   При малых различиях в значениях молекулярной массы компонентов величина коэффициента теплопроводности смеси подчиняется условию аддитивности:
   

2. 
   При большом различии молекулярных масс компонентов (смеси водорода) лучшее согласование с опытом дает логарифмическая зависимость
   

или

3. 
   Во всех остальных случаях истинное значение находится в области, ограниченной вышеприведенными значениями, т. е.
   

1.4.11.2. Многокомпонентные смеси

• 
  Коэффициент динамической вязкости многокомпонентной смеси можно определить с использованием методов Гиршфельдера и его школы [3].
  

Эти методы дают хорошее согласование с опытом, особенно для коэффициента вязкости, но используют громоздкие и неудобные для практики формулы. В связи с этим получили распространение более простые аппроксимационные формулы, например, приближенная формула Уилке [4]: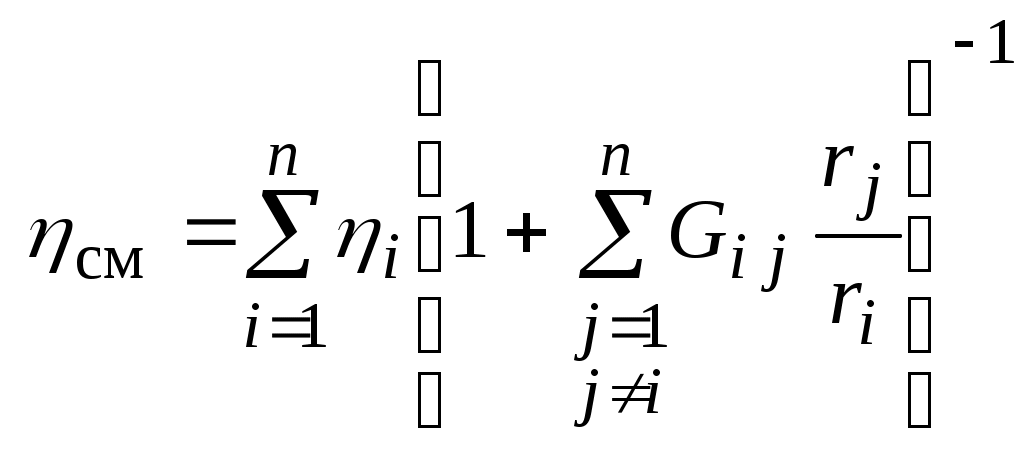
,
где: 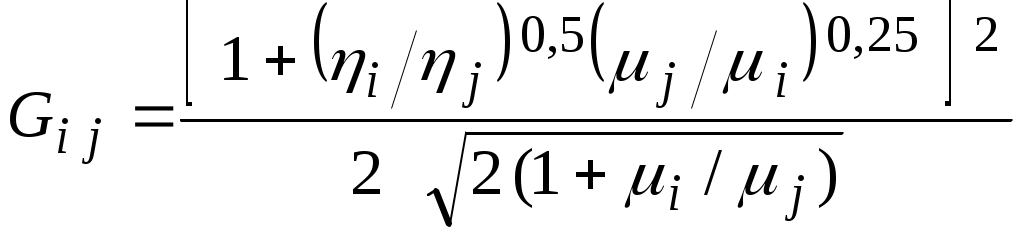- мольная (объемная) концентрация i-го компонента смеси.

Погрешность результатов расчетов по формуле Уилке по сравнению с опытом находится в пределах 4%.

Коэффициент теплопроводности -компонентной газовой смеси можно определить по приближенной формуле Масона-Саксена [4]:

• 
  В работе [5] для газовых смесей рекомендуется формула Брокау:
  

где: и

2. СМЕШЕНИЕ ГАЗОВ
Пусть смешиваются nхимически невзаимодействующих между собой идеальных газов. Предполагается, что известны начальные термодинамические параметры состояния всех компонентов до смешения и условия смешения (условия взаимодействия с окружающей средой). Требуется найти равновесные параметры состояния газов после смешения.

Рассмотрим два случая смешения, для простоты полагая, что этот процесс идет без теплообмена с окружающей средой.


2.1. Смешение при W=Const
В этом случае условия смешения таковы, что объем образующейся смеси W_см равен сумме начальных объемов компонентов смеси W_Hi:
.
(Не следует путать W_Hi с парциальными объемами W_i, рассмотренными в параграфе 1.4.3.)
Обозначим:

Р_Hi – начальное давление i-го газа;

Т_Hi,t_Hi– начальная температура i-го газа соответственно в ⁰К или ⁰С.

Т.к. вся система из n газов при смешении в условиях W=Constне совершает внешней работы, то в соответствии с первым началом термодинамики для этого случая ( ) можно записать:
(2.1.1)
Здесь: U_см – внутренняя энергия смеси газов массой m_см килограммов

с температурой Т⁰ К;

U_Hi - внутренняя энергия i-го газа массой m_i килограммов

с начальной температурой Т_Hi .

Введем обозначения:

u_см – удельная внутренняя энергия смеси газов при температуре Т⁰ К;

u_Hi– удельная внутренняя энергия i-го газа с начальной температурой Т_Hi.

Тогда уравнение (2.1.1) принимает следующий вид:
(2.1.2)
Как известно, для идеального газа du=C_vdT , откуда при отсчете внутренней энергии от 0⁰ К можно записать:
и . (2.1.3)
Здесь: - средняя в диапазоне 0 Т⁰ К массовая изохорная теплоемкость смеси газов;



- средняя в диапазоне 0 Т_Hi⁰К массовая изохорная теплоемкость i-го газа.
После подстановки (2.1.3) в (2.1.2) получим:
. (2.1.4)
Но в соответствии с параграфом 1.4.10 истинная массовая теплоемкость смеси газов выражается через массовые доли компонентов g_i и их истинные теплоемкости следующим образом:
.
Аналогично средняя в диапазоне 0 Т⁰ К массовая изохорная теплоемкость смеси газов определится как:
.
Подставляя это выражение в левую часть уравнения (2.1.4) получим:

,
откуда 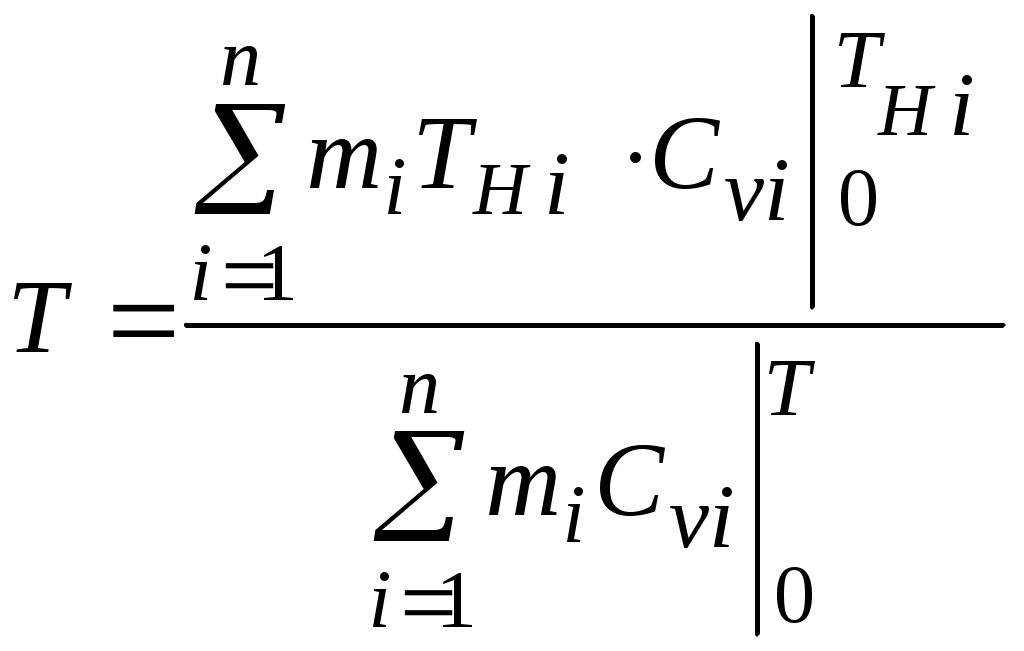(2.1.5)
Т.к. из уравнения состояния 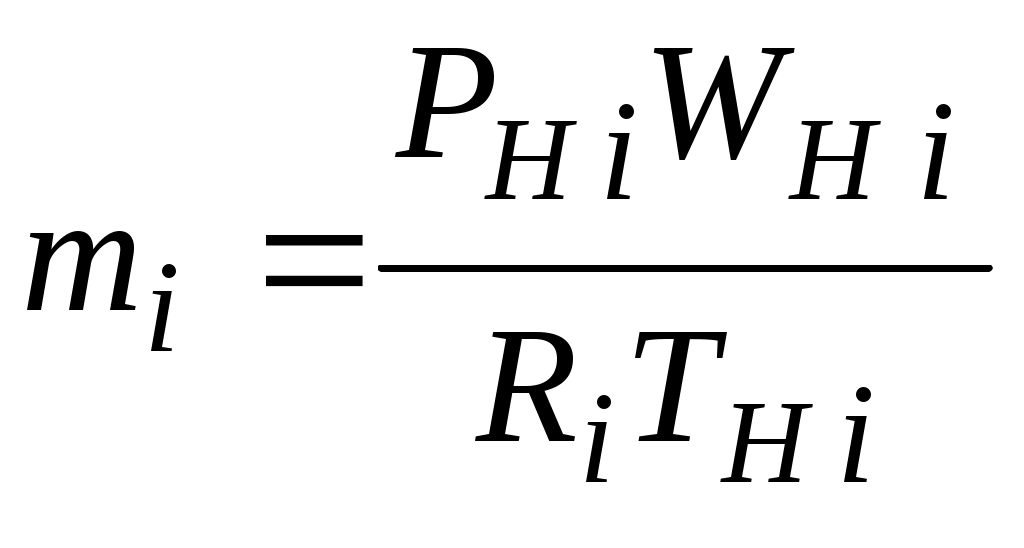, то после подстановки m_i в уравнение (2.1.5) окончательно получим формулу для температуры смеси n газов: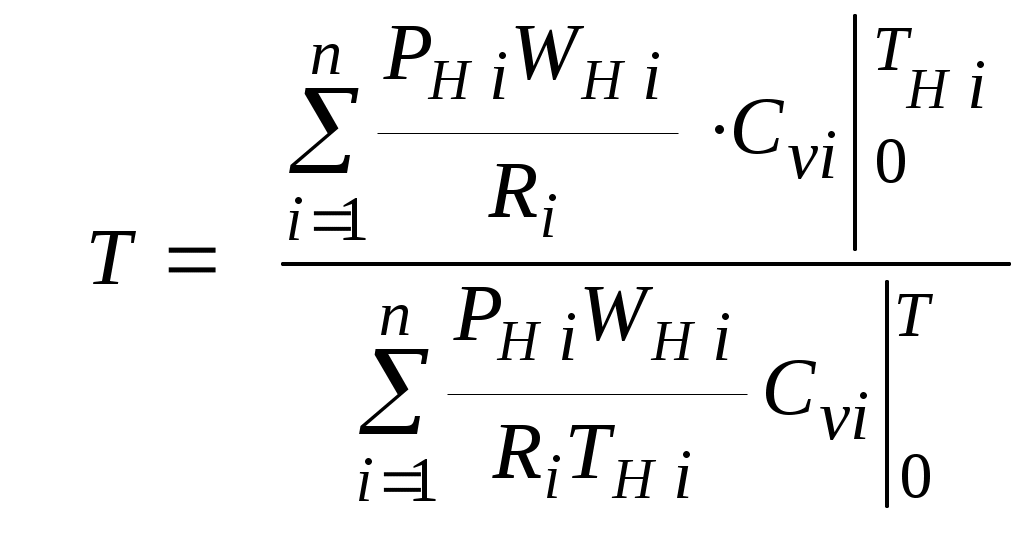
(2.1.6)

Как известно, 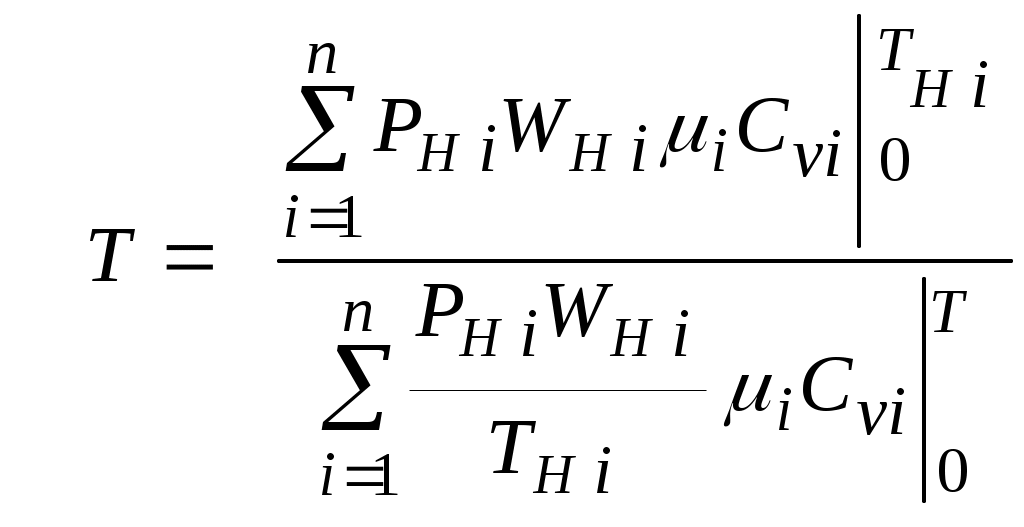, поэтому формула (2.1.6) может быть записана в следующем виде:
(2.1.7)
(Следует напомнить, что произведение 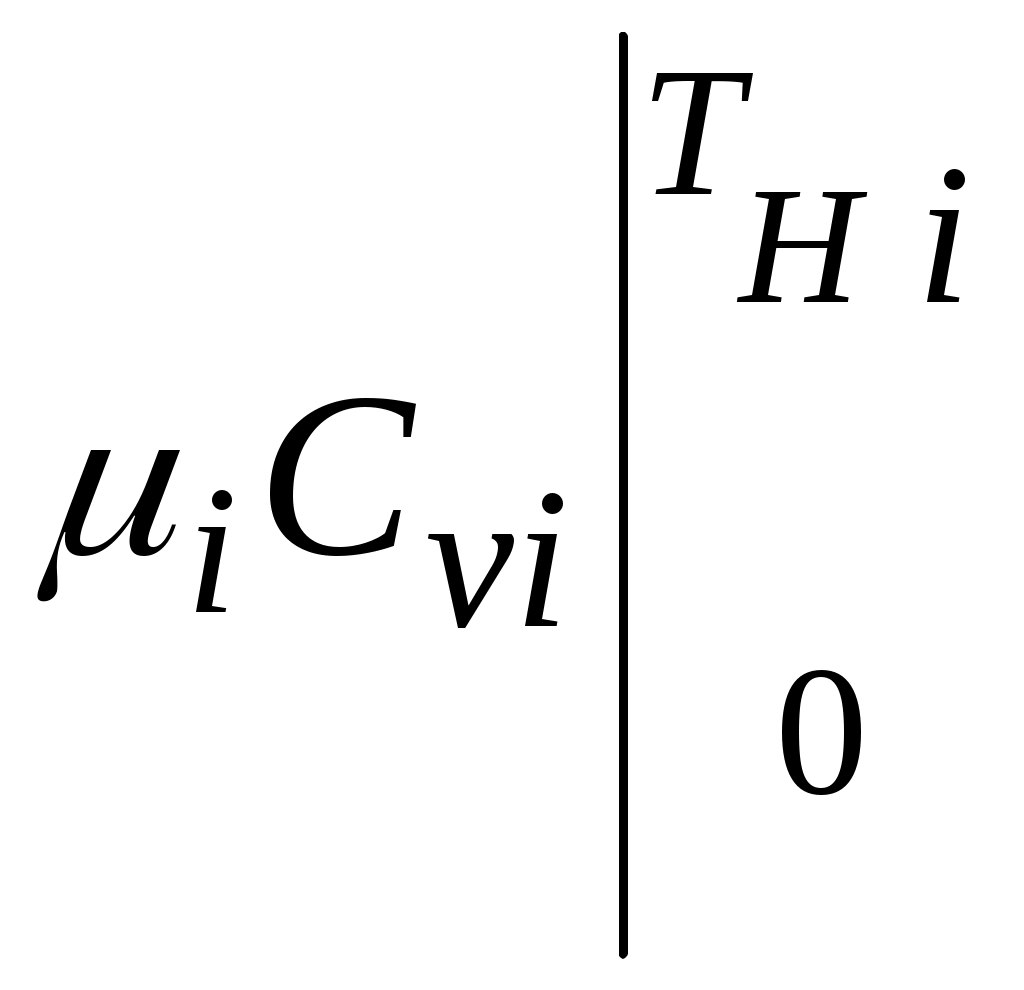- это средняя в диапазоне 0- Т_Hi⁰К молярная изохорная теплоемкость i-го газа.)

В справочной литературе эмпирические зависимости теплоемкости от температуры часто даются для диапазона 0 t⁰ С.

Тогда:
и , (2.1.8)
где (2.1.9)
После подстановки (2.1.8) и (2.1.9) в уравнение (2.1.2) получим:
,
откуда .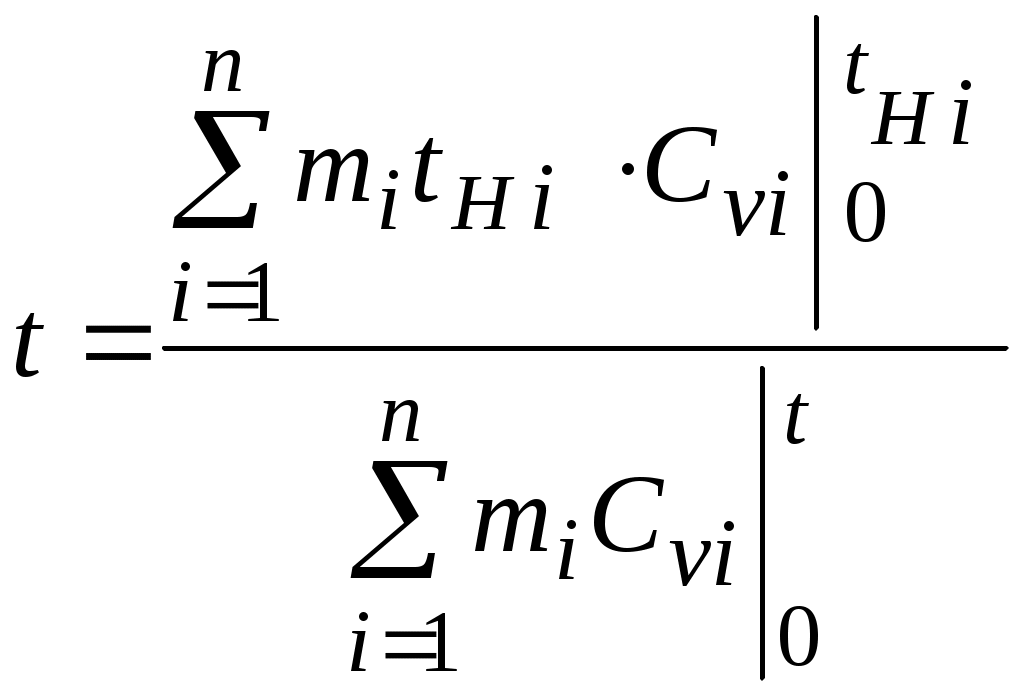
Заменяя m_i его значением 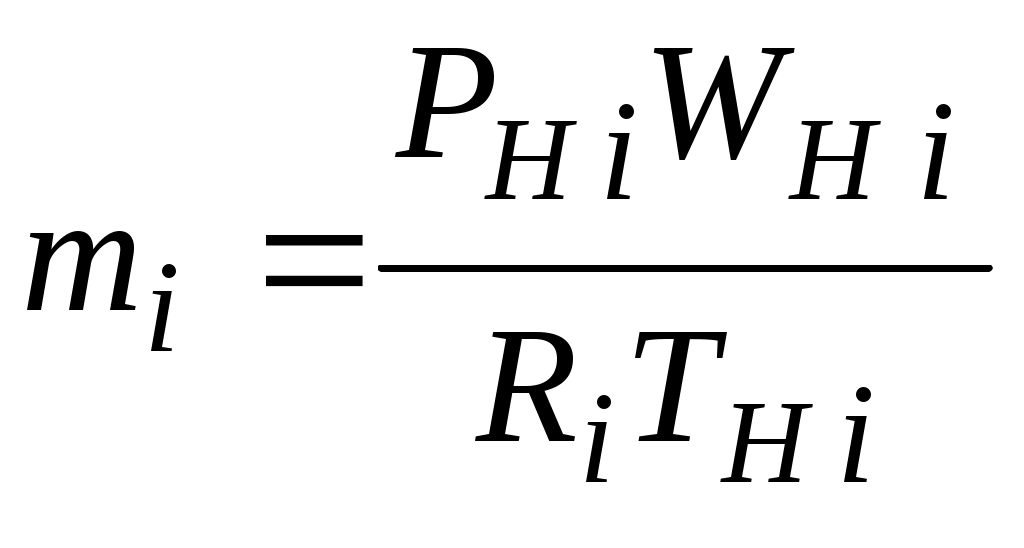, окончательно получим формулу для температуры смеси газов в градусах Цельсия: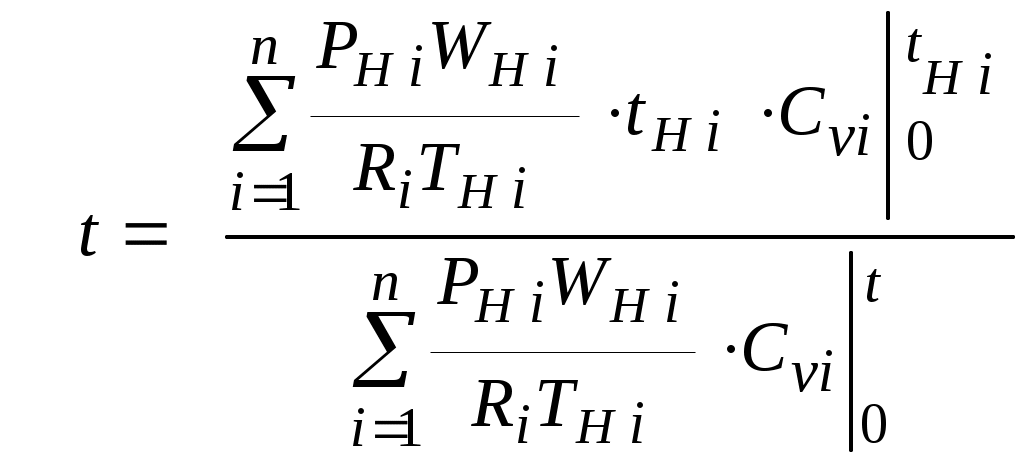
(2.1.10)
Выражая R_i через малекулярную массу 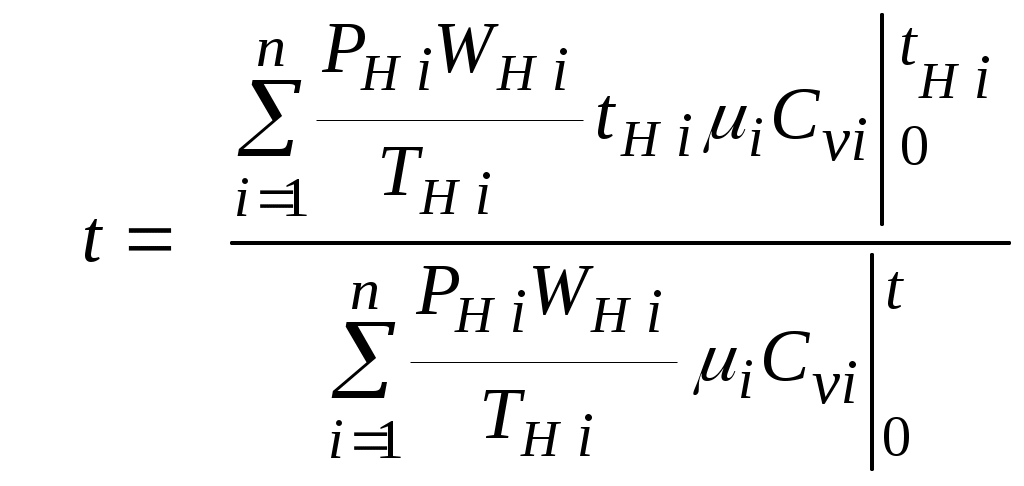, получим еще одну формулу:
(2.1.11)
В знаменателях формул (2.1.6), (2.1.7), (2.1.10) и (2.1.11) содержатся средние теплоемкости, у которых в качестве верхнего предела осреднения используется температура смеси (t или Т), подлежащая определению. В силу этого, температура смеси по этим формулам определяется методом последовательных приближений.