теплофизика. Решение Молекулярная масса смеси газов см r О2 О2 r h 2 h 2 r n 2 N

• Название: Решение Молекулярная масса смеси газов см r О2 О2 r h 2 h 2 r n 2 N
• Анкор: теплофизика
• Дата: 11.06.2022
• Размер: 36.46 Kb.
• Имя файла: теплофизика.docx
• Тип: Решение; #585240

Вариант №03
Задача 1

Определить массовые доли, плотности и парциальные давления газов, входящих в смесь, а также молекулярную массу, газовую постоянную и плотность смеси, состав которой задан объемными долями.

Дано: r_O2 = 0,4; r_H2 = 0,2; r_N2 = 0,2; r_CO2 = 0,2; p_cм = 0,9 МПа; Т_см = 343 К

Найти: g_i; _i; p_i; _см; R_см; _см

Решение:

Молекулярная масса смеси газов

_см = r_О2_О2 + r_H2_H2 + r_N2_N2 + r_СО2_СО2 =

= 0,40,032 + 0,20,002 + 0,20,028 + 0,20,044 = 0,0276 кг/моль,

где _О2 = 0,032 кг/моль – молярная масса кислорода;

_Н2 = 0,002 кг/моль – молярная масса водорода;

_N2 = 0,028 кг/моль – молярная масса азота;

_СО2 = 0,044 кг/моль – молярная масса углекислого газа.

Массовые доли компонентов смеси газов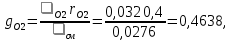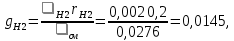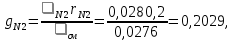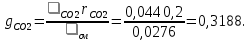









Проверка:

g_O2 + g_H2 + g_N2 + g_CO2 = 0,4638 + 0,0145 + 0,2029 + 0,3188 = 1,0.

Газовая постоянная смеси газов

R_см = R_ / _см = 8,314 / 0,0276 = 301,2 Дж/(кгК),

где R_ = 8,314 Дж/(мольК) – универсальная газовая постоянная.
Парциальные давления компонентов смеси

р_O2 = р_cмr_O2 = 0,90,4 = 0,36 МПа,

р_H2 = р_cмr_H2 = 0,90,2 = 0,18 МПа,

р_N2 = р_cмr_N2 = 0,90,2 = 0,18 МПа,

р_СO2 = р_cмr_СO2 = 0,90,2 = 0,18 МПа.

Проверка:

р_O2 + р_H2 + р_N2 + р_СO2 = 0,36 + 0,18 + 0,18 + 0,18 = 0,9 МПа = р_см.

Газовые постоянные компонентов смеси газов

R_О2 = R_ / _О2 = 8,314 / 0,032 = 259,8 Дж/(кгК),

R_Н2 = R_ / _Н2 = 8,314 / 0,002 = 4157 Дж/(кгК),

R_N2 = R_ / _N2 = 8,314 / 0,028 = 296,9 Дж/(кгК),

R_CO2 = R_ / _CO2 = 8,314 / 0,044 = 189,0 Дж/(кгК),

Плотности компонентов смеси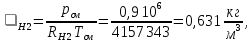









где T_см = 343 К – термодинамическая температура смеси газов;

р_см = 0,9 МПа = 0,910⁶ Па – давление смеси газов.

Плотность смеси газов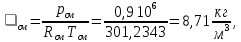



Проверка:

_см = _ir_i = 10,10,4 + 0,6310,2 + 8,8380,2 + 13,880,2 = 8,71 кг/м³


Задача 2

Воздух массой m при начальном абсолютном давлении p₁ и температуре T₁ расширяется в политропном процессе до давления p₂. Показатель политропы расширения n.

Определить конечные объем V₂ и температуру Т₂ воздуха после расширения, количество отведенной теплоты, изменение энтропии и внутренней энергии, а также долю теплоты, идущей на совершение внешней работы. Показатель адиабаты принять k =1,4.

Это же задание выполнить для адиабатного процесса.

Дано: m = 10 кг; р₁ = 1,510⁶ Па; р₂ = 0,510⁶ Па; Т₁ = 500 К; n = 1,25; k = 1,4

Найти: V₂; Т₂; Q; S; U; 

Решение:

Газовая постоянная воздуха

R = R_ /  = 8,314 / 0,029 = 287 Дж/(кгК),

где  = 0,029 кг/моль – молярная масса воздуха;

R_ = 8,314 Дж/(мольК) – универсальная газовая постоянная.

Начальный объем воздуха определяем из уравнения Менделеева-Клапейрона



где m = 10 кг – масса воздуха;

T₁ = 500 К – начальная температура воздуха;

р₁ = 1,510⁶ Па – начальное давление воздуха.

1. 
   Политропный процесс (n = 1,25)
   

Температуру воздуха в конце политропного расширения определяем из уравнения политропного процесса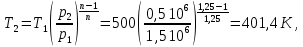



где n = 1,25 – показатель политропы.

Объем воздуха в конце политропного расширения определяем из уравнения политропного процесса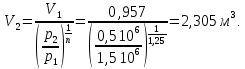



Температура воздуха в начале и конце процесса расширения

t₁ = T₁ – 273 = 500 – 273 = 227 ⁰C,

t₂ = T₂ – 273 = 401,4 – 273 = 128,4 ⁰C

Среднюю изохорную теплоемкость воздуха в диапазоне температур 0…t₁ определяем интерполированием по Приложению 2 [1]: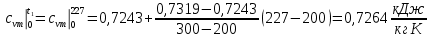



Среднюю изохорную теплоемкость воздуха в диапазоне температур 0…t₂ определяем интерполированием по Приложению 2 [1]: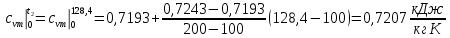



Средняя массовая изохорная теплоемкость воздуха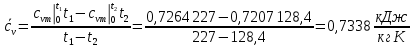



Изменение энтропии в политропном процессе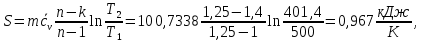



где k = 1,4 – показатель адиабаты воздуха.

Изменение внутренней энергии в политропном процессе

U = m (T₂ – T₁) = 100,7338(401,4 – 500) = –723,5 кДж.

Внешняя работа расширения в политропном процессе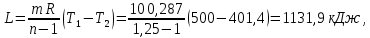



Количество теплоты, отведенной в политропном процессе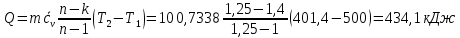



Доля теплоты, пошедшей на совершение внешней работы

 = Q / L = 434,1 / 1131,9 = 0,384.

2. 
   Адиабатный процесс
   

Температуру воздуха в конце адиабатного расширения определяем из уравнения адиабатного процесса



Объем воздуха в конце адиабатного расширения определяем из уравнения адиабатного процесса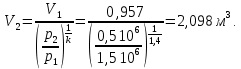



Температура воздуха в конце процесса адиабатного расширения

t₂ = T₂ – 273 = 365,3 – 273 = 92,3 ⁰C

Среднюю изохорную теплоемкость воздуха в диапазоне температур 0…t₂ определяем интерполированием по Приложению 2 [1]:



Средняя массовая изохорная теплоемкость воздуха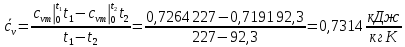



Изменение энтропии в адиабатном процессе равно нулю, так как в адиабатном процессе нет теплообмена с окружающей средой:



Изменение внутренней энергии в адиабатном процессе

U = m (T₂ – T₁) = 100,7314(365,3 – 500) = –985,2 кДж.

Внешняя работа расширения в адиабатном процессе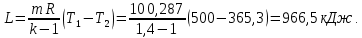



Количество теплоты, отведенной в адиабатном процессе равно нулю, так как в адиабатном процессе нет теплообмена с окружающей средой: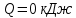



Доля теплоты, пошедшей на совершение внешней работы

 = Q / L = 0 / 966,5 = 0.

Задача 3

Определить коэффициент теплоотдачи, плотность теплового потока и тепловой поток от воды к стенке трубы диаметром d и длиной L. Скорость воды w, ее температура t_ж, а температура стенки t_ст.

Дано: d = 15 мм; L = 3 м; w = 2,5 м/с; t_ж = 70 ⁰С; t_ст = 10 ⁰С

Найти: , q, Q

Решение:

Критерий Рейнольдса воды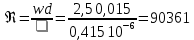



где  = 0,41510^-6 м²/с – коэффициент кинематической вязкости воды при температуре воды t_ж = 70 ⁰С (Приложение 3 [1]);

w = 2,5 м/с – скорость воды;

d = 15 мм = 0,015 м – диаметр трубы.

Так как Re > 10⁴, следовательно, режим течения воды турбулентный.

Определяем критерий Нуссельта из критериального уравнения для вынужденного турбулентного движения жидкости внутри трубы

Nu = 0,021Re^0,8Pr^0,43(Pr / Pr_cт)^0,25Е_L =

= 0,02190361^0,82,55^0,43(2,55 / 9,52)^0,251 = 208,3,

где Pr = 2,55 – критерий Прандтля воды при температуре воды t_ж = 70 ⁰С (Приложение 3 [1]);

Pr_ст = 9,52 – критерий Прандтля воды при температуре воды, равной температуре стенки t_ст = 10 ⁰С (Приложение 3 [1]);

Е_L = 1 – коэффициент, учитывающий начальный неизотермический участок трубы равен 1, так как отношение длины трубы к ее диаметру L/d=3/0,015=200>50.

Коэффициент теплоотдачи от воды к стенке трубы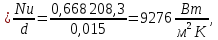



где  = 0,668 Вт/(мК) – коэффициент теплопроводности воды при температуре воды t_ж = 70 ⁰С (Приложение 3 [1]).

Плотность теплового потока

q = (t_ж – t_ст) = 9276(70 – 10) = 556560 Вт/м²  556,6 кВт/м²,

где t_ж = 70 ⁰С – температура воды внутри трубы;

t_ст = 10 ⁰С – температура стенки трубы.

Площадь поверхности трубы

F = dL = 3,140,0153 = 0,1413 м²,

где L = 10 м – длина трубы.

Тепловой поток от воды к стенке трубы

Q = qF = 556,620,1413 = 78,65 кВт.
Ответ:  = 9276 Вт/(м²К); q = 556,6 кВт/м²; Q = 78,65 кВт.