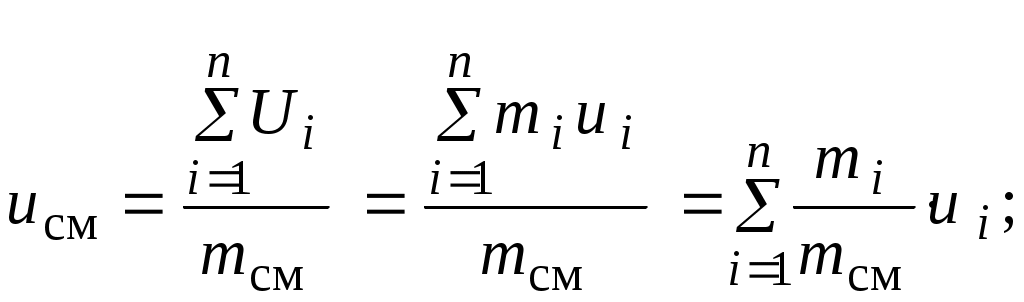ГАЗОВЫЕ СМЕСИ
Газовые смеси встречаются в технике чаще, нежели чистые газы.
Так к газовым смесям относится атмосферный воздух, состоящий из азота, кислорода, углекислого газа, водяного пара и других газов.
Природный газ также является смесью предельных и непредельных углеводородов, оксида углерода, водорода, сероводорода, азота, кислорода, углекислого газа и других газов.
К газовым смесям относятся также продукты сгорания топлива в котлоагрегатах (дымовые газы), состоящие из углекислого газа, паров воды, азота, кислорода и других газов.
Вычисление термодинамических параметров состояния и теплофизических характеристик газовых смесей является обязательным элементом при решении большого числа инженерных и научных задач.
1.1. Основные признаки газовых смесей
Основные признаки смеси газов (идеальных и реальных) следующие:
гомогенность, т. е. внутри системы нет макроскопических частей (подсистем), отделенных друг от друга поверхностями раздела;
физическая однородность, т.е. состав и физические свойства системы одинаковы для всех ее макроскопических частей, равных по объему;
все компоненты смеси находятся в одной фазе (агрегатном состоянии);
термодинамические параметры смеси (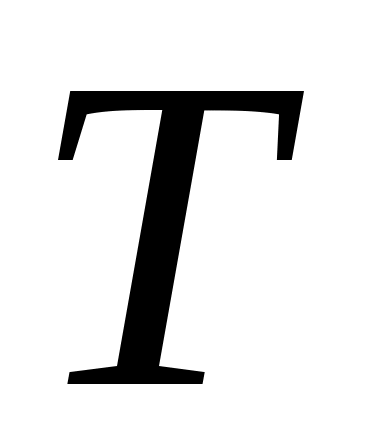 , , 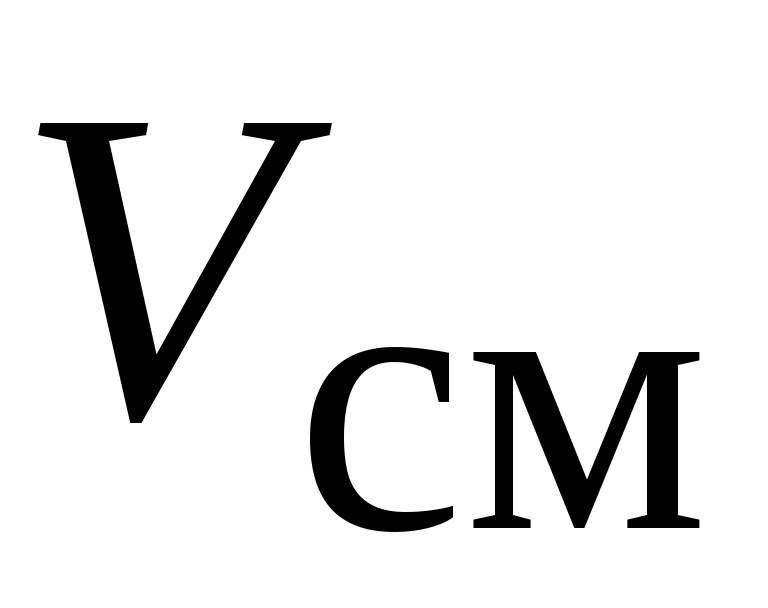 ) связаны между собой уравнением состояния, общий вид которого : ) связаны между собой уравнением состояния, общий вид которого : 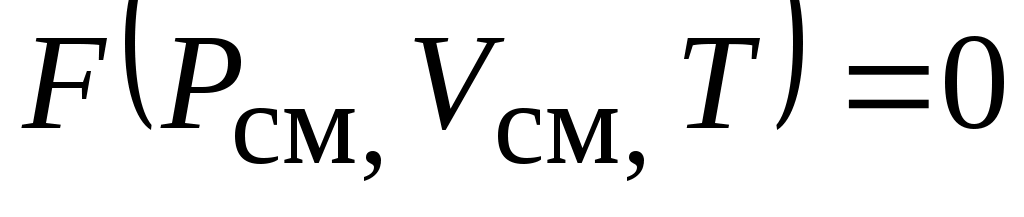 , здесь: , здесь: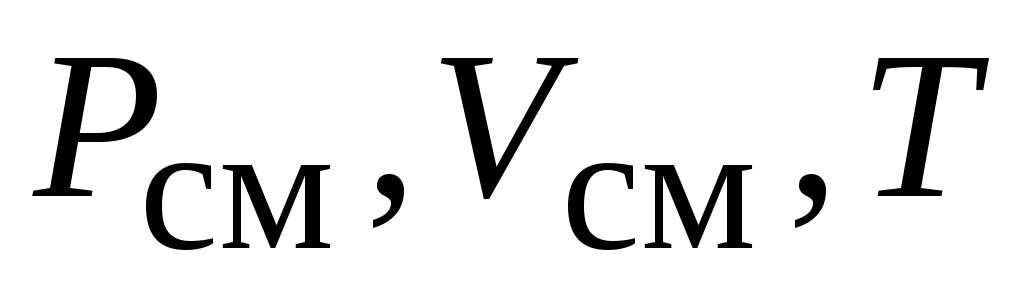 - температура, удельный объем и температура смеси. - температура, удельный объем и температура смеси.
компоненты смеси не вступают между собой в химические реакции, т. е. представляют механическую смесь;
каждый газ смеси распределяется равномерно по всему объему смеси  , сохраняя свои свойства; , сохраняя свои свойства;
все газы смеси имеют в состоянии равновесия одинаковую температуру, равную температуре смеси 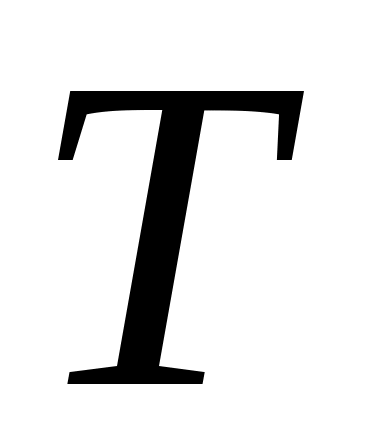 ; ;
каждый газ смеси подчиняется уравнению состояния, аналогичному уравнению состояния смеси. При этом все газы, входящие в смесь, в зависимости от плотности смеси считаются либо реальными, либо идеальными.
Т.о. смесь газов - это гомогенная термодинамическая система, представляющая собой совокупность нескольких разнородных газов, которые при рассматриваемых условиях не вступают друг с другом в химические реакции.
1.2. Основные понятия и определения газовых смесей
Компоненты смеси - это газы, образующие смесь.
Молем (грамм-молекулой) называется количество химически однородного вещества в граммах, численно равное его молекулярной массе 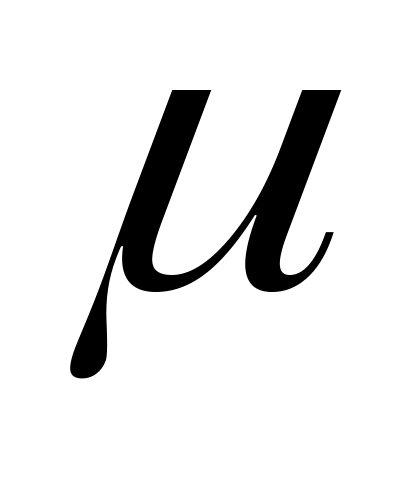 . .
Киломолем (килограмм-молекулой) называется количество химически однородного вещества в килограммах, численно равное его молекулярной массе 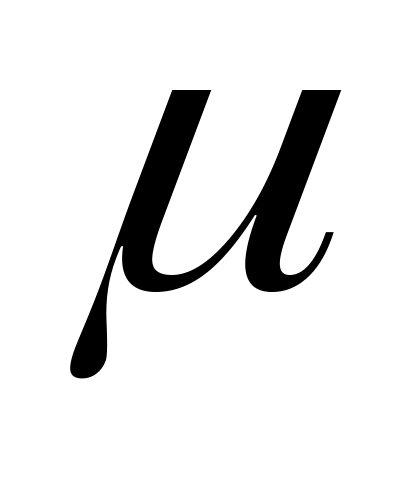 . .
Идеальный газ – это газ, в котором отсутствуют силы межмолекулярного взаимодействия, а молекулы не имеют размера (материальные точки). Последнее означает, что размеры молекул по сравнению с межмолекулярным пространством пренебрежимо малы.
Поведение реальных газов приближается к идеальному только при малых плотностях. В остальных случаях необходим учет межмолекулярного взаимодействия и конечного объема молекул.
1.3. Способы задания состава смеси реальных газов
Состав 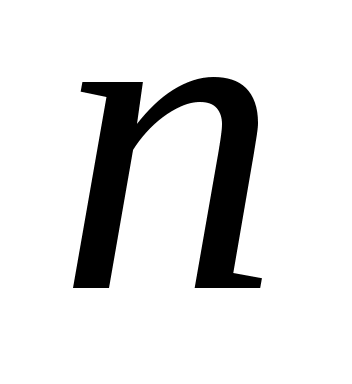 - компонентной смеси реальных газов задается либо массвыми, либо мольными долями i-тых газов, входящих в смесь - компонентной смеси реальных газов задается либо массвыми, либо мольными долями i-тых газов, входящих в смесь
(i = 1,2, …. , 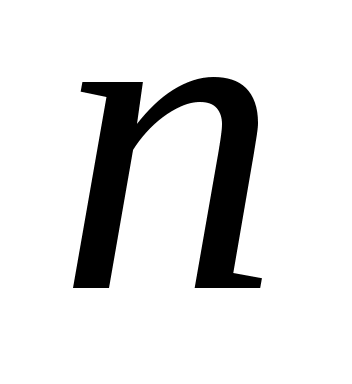 ) )
Массовая доля 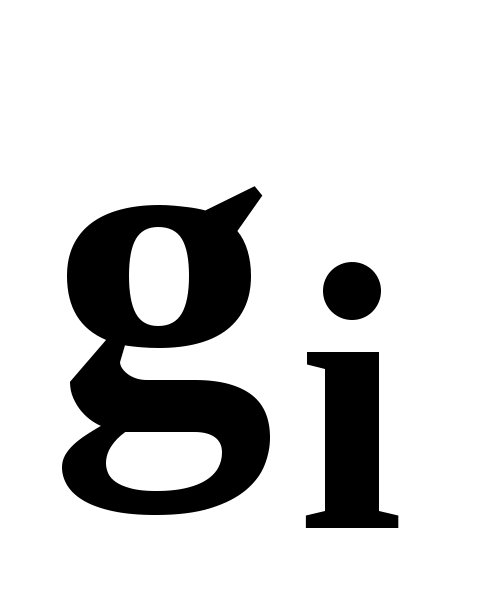 (массовая концентрация, массовая долевая концентрация) – это отношение массы i-го компонента смеси (массовая концентрация, массовая долевая концентрация) – это отношение массы i-го компонента смеси 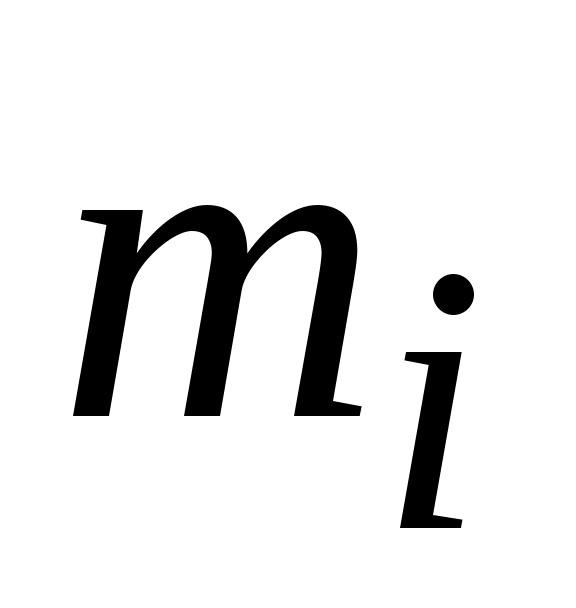 к массе всей смеси к массе всей смеси 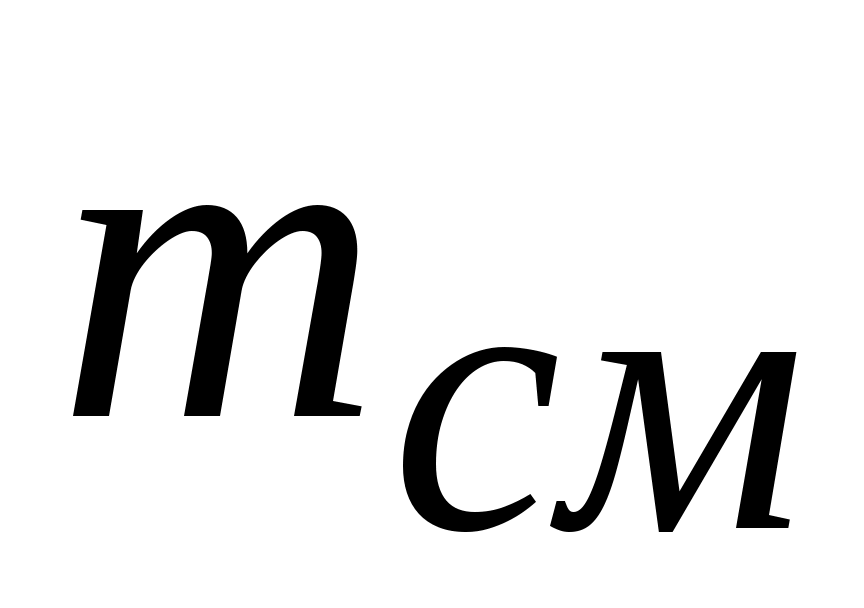 : :
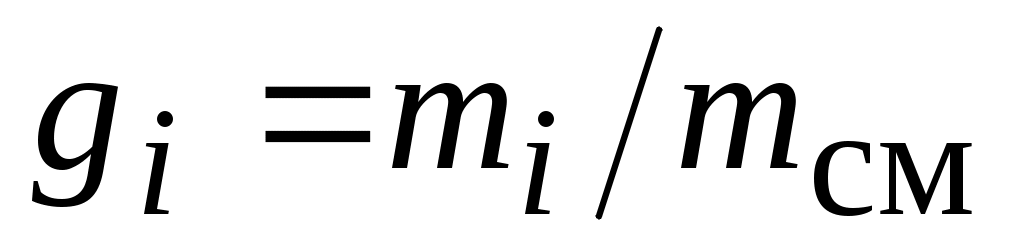  , ,
где:
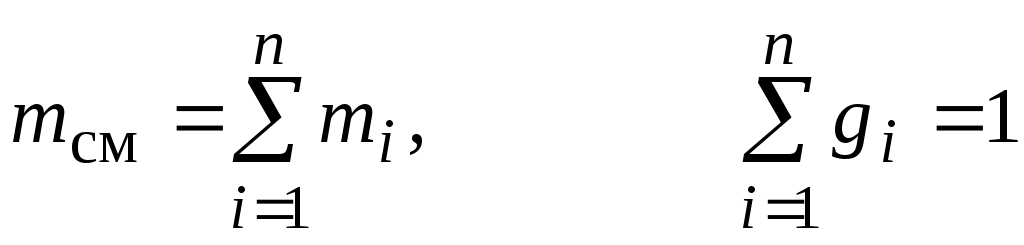
Мольная (молярная) доля 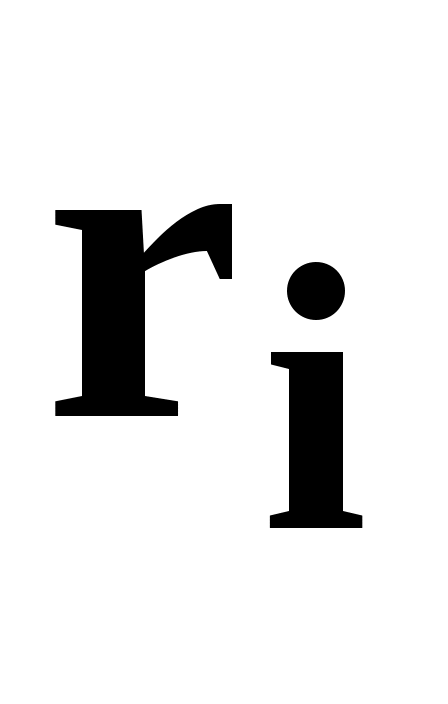  (мольная (молярная) концентрация, мольная (молярная) долевая концентрация) – это отношение числа киломолей (молей) i- го компонента к суммарному числу киломолей (молей) всех газов в (мольная (молярная) концентрация, мольная (молярная) долевая концентрация) – это отношение числа киломолей (молей) i- го компонента к суммарному числу киломолей (молей) всех газов в
смеси 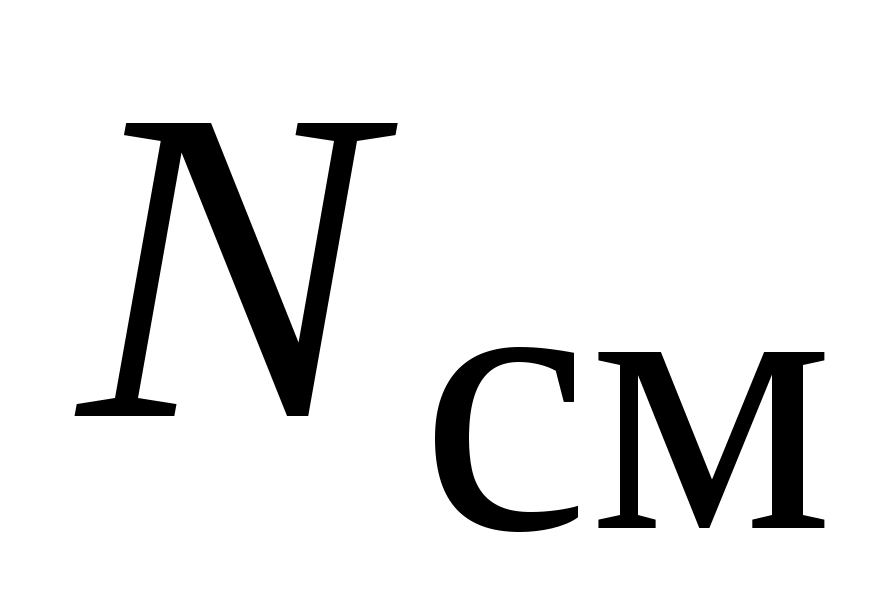 : :
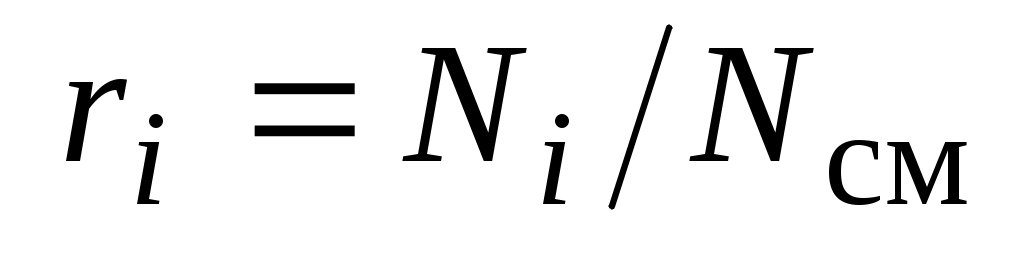 , ,
где: 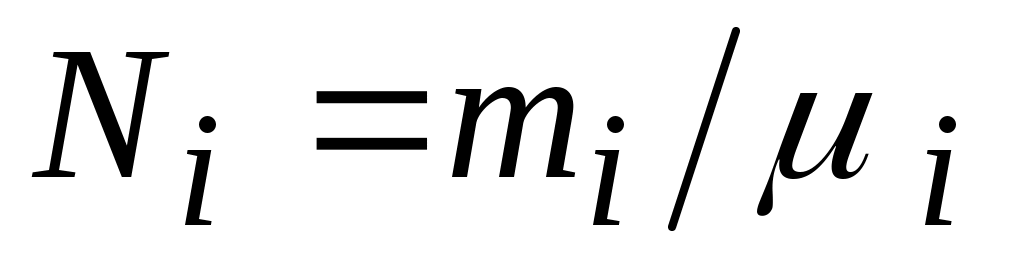 ; ; 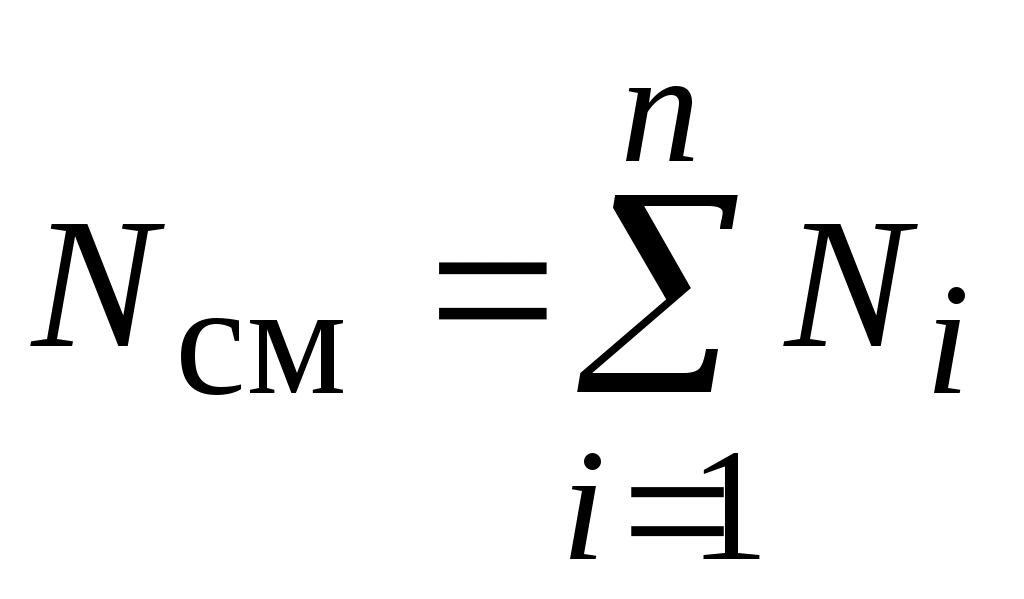 ; ; 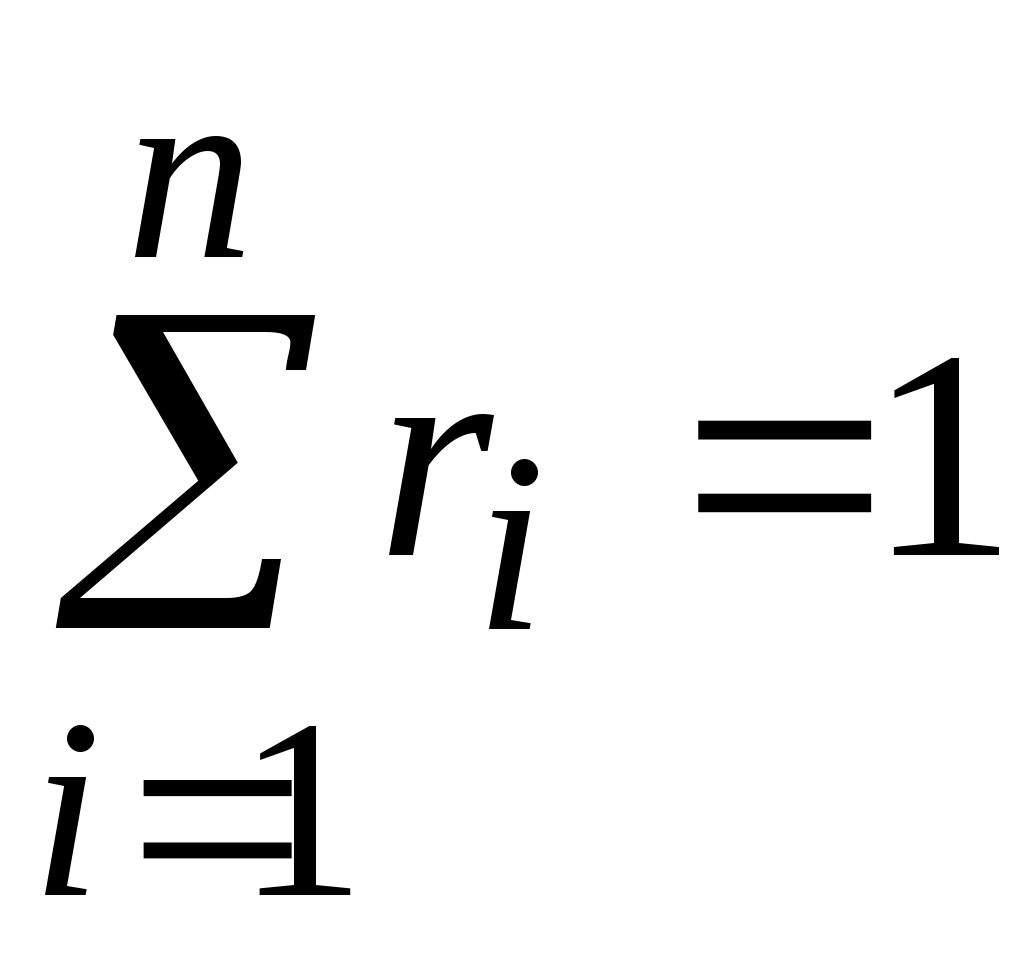 ; ;
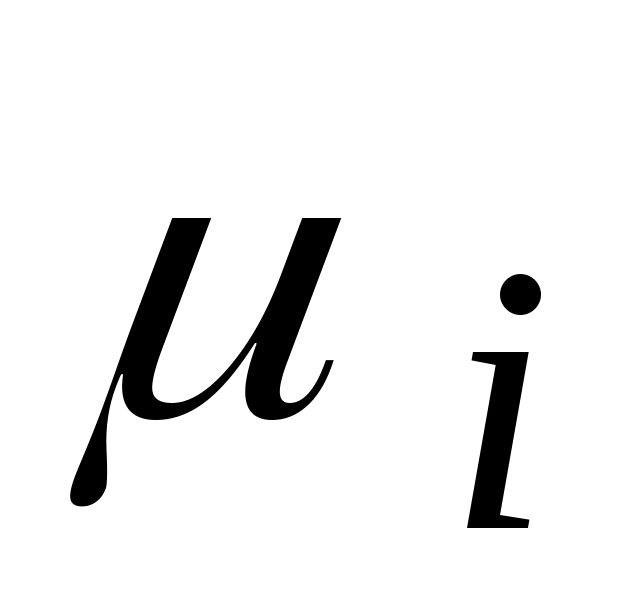 - молекулярная масса i-го газа. - молекулярная масса i-го газа.
1.4. Смеси идеальных газов
1.4.1. Характеристические функции и функции состояния газовых
смесей
1.4.1.1. Удельные значения функций и параметров смеси газов
Каждый из идеальных газов ведет себя в смеси автономно, т. е. так, будто других газов нет. Отсутствие межмолекулярного взаимодействия у идеальных газов обусловливает независимость их свойств от других газов, составляющих смесь. Следствием этой независимости свойств идеальных газов в смеси является строгая аддитивность таких термодинамических величин смеси как давление, внутренняя энергия, энтальпия и т. д.
(Термин « аддитивный » происходит от латинского additivus - полученный путем сложения)
Т. о. вышеперечисленные термодинамические величины для всей смеси получаются путем арифметического сложения соответствующих величин всех компонентов смеси. Примеры аддитивности:
Пример1.
Масса смеси:
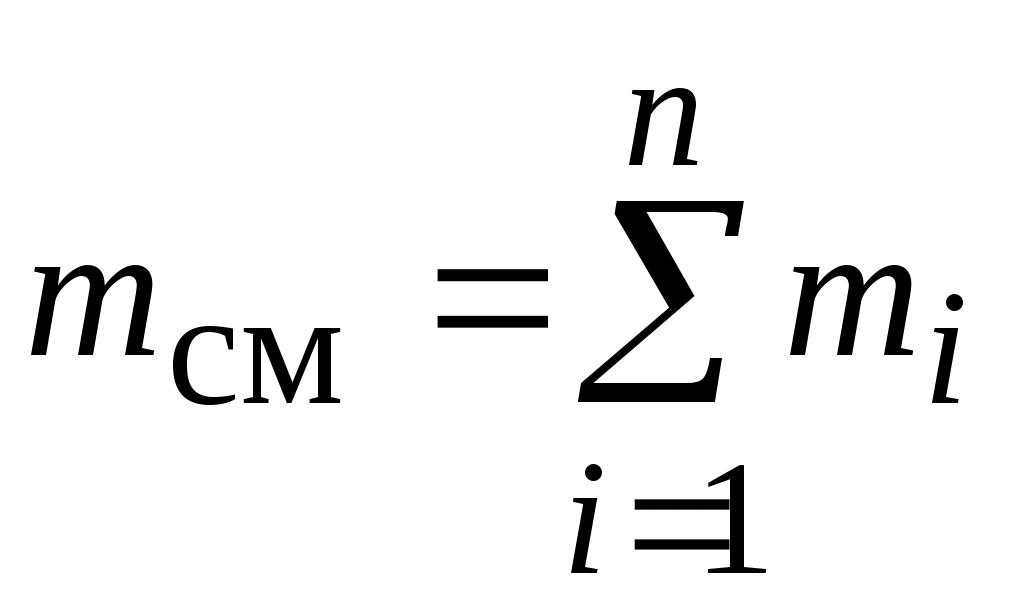 . .
Пример2.
Внутренняя энергия  смеси n газов массой смеси n газов массой 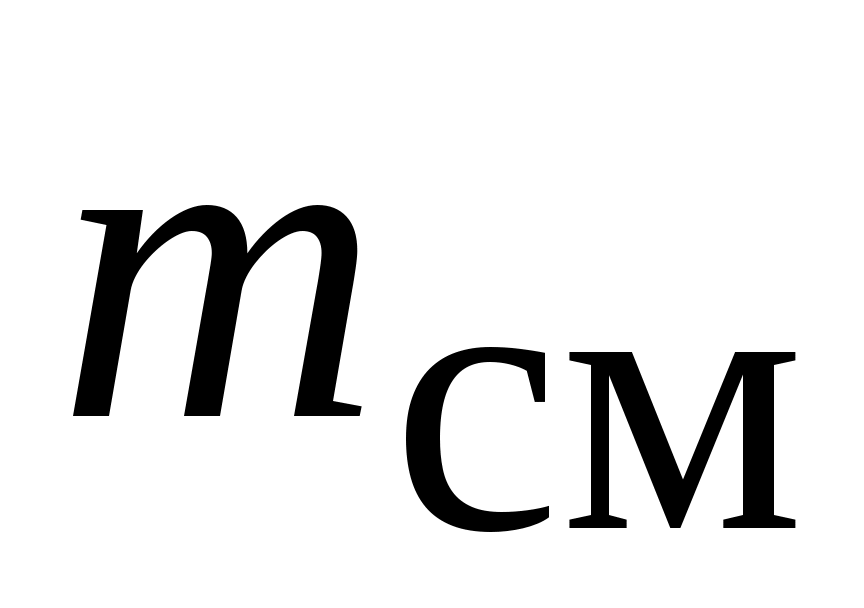 , занимающих объем , занимающих объем  , равна: , равна:
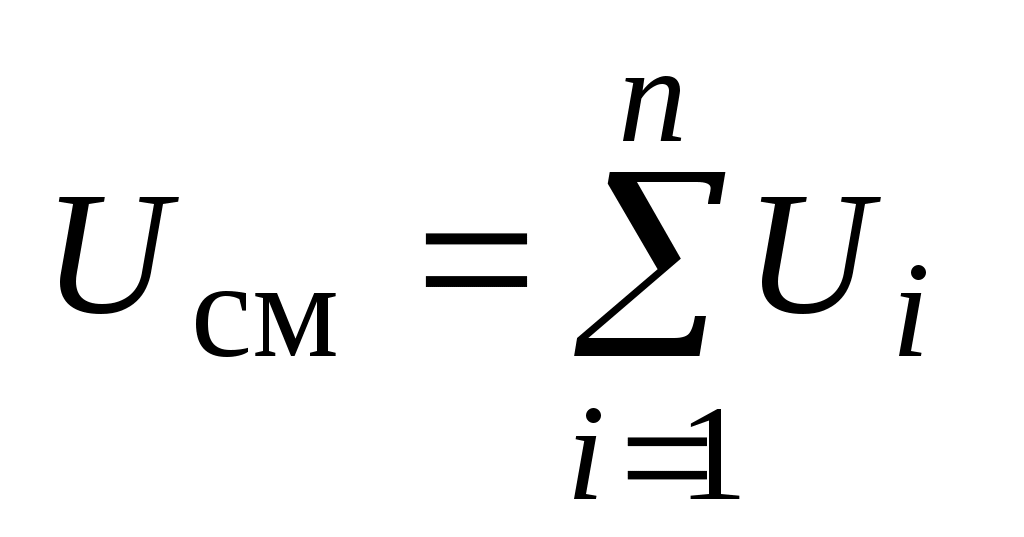 , ,
где: 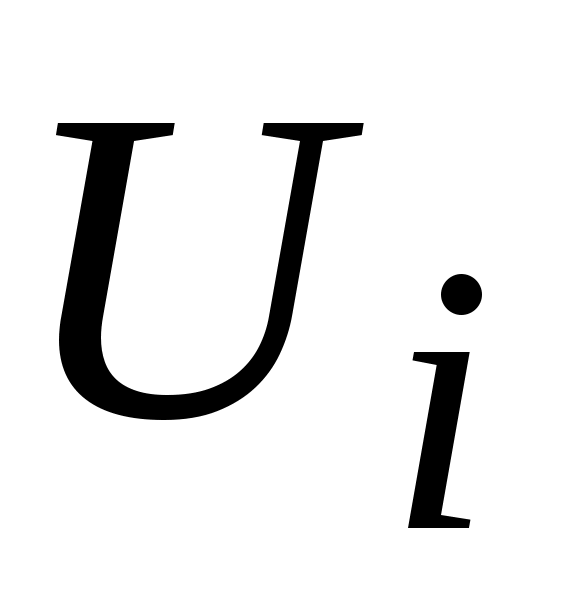 - внутренняя энергия - внутренняя энергия 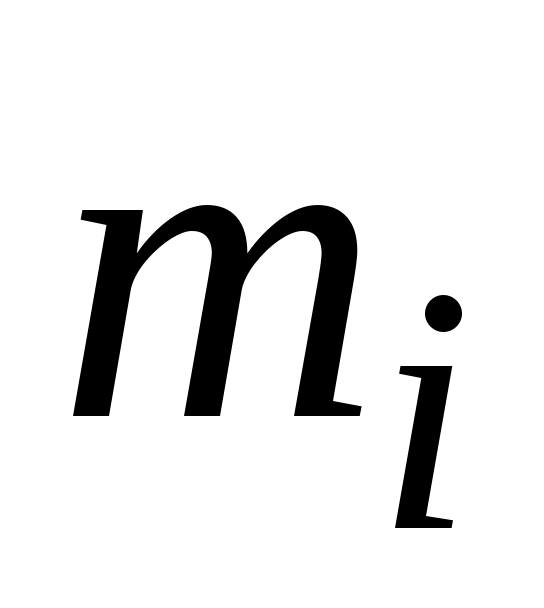 килограммов i-го газа в составе килограммов i-го газа в составе
смеси, Дж
Обозначим:
uсм - удельная внутренняя энергия смеси газов (внутренняя энергия одного кг смеси), Дж / кг;
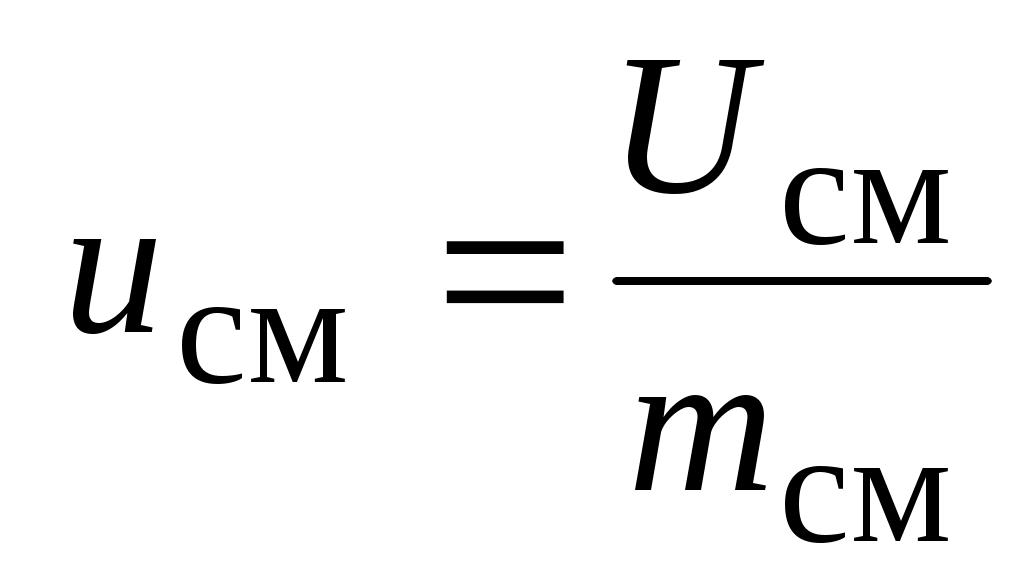 , ,
ui- удельная внутренняя энергия i-го газа смеси, Дж / кг
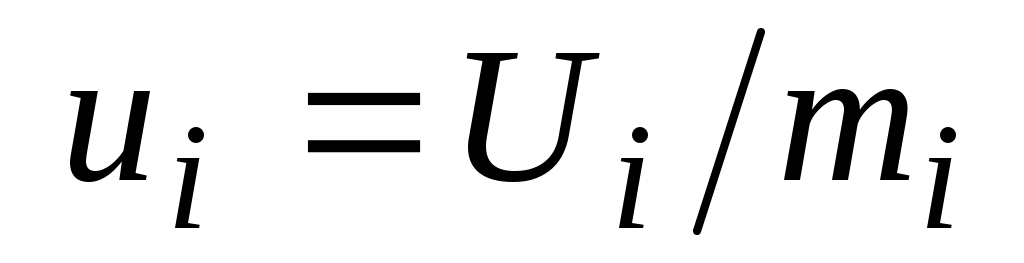 . .
Тогда:
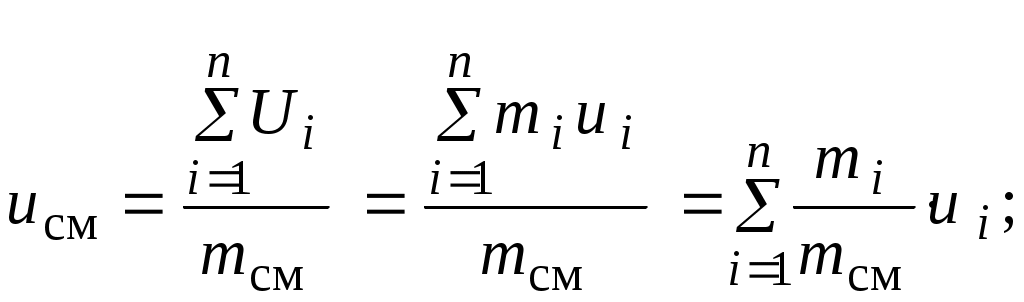
Окончательно:
 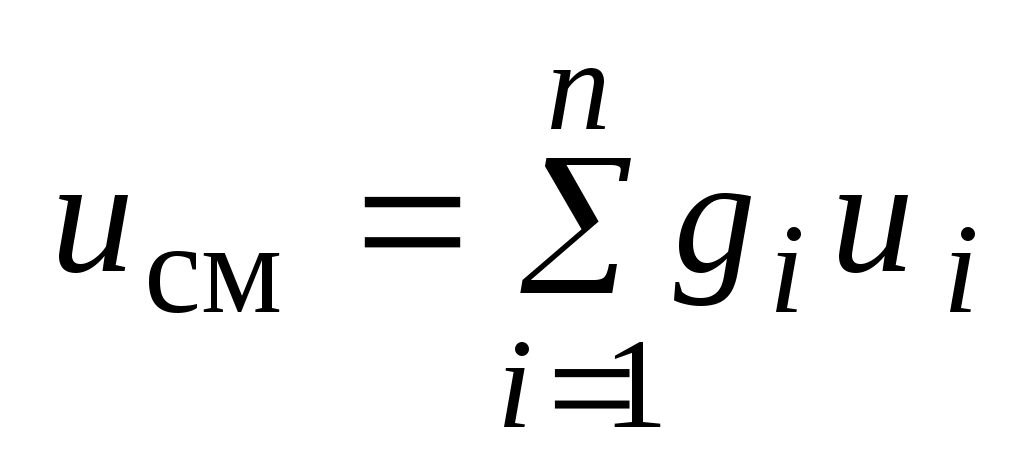 . .
Пример3.
Энтальпия смеси 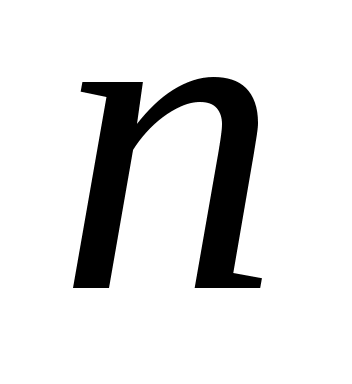 газов газов  , Дж : , Дж :
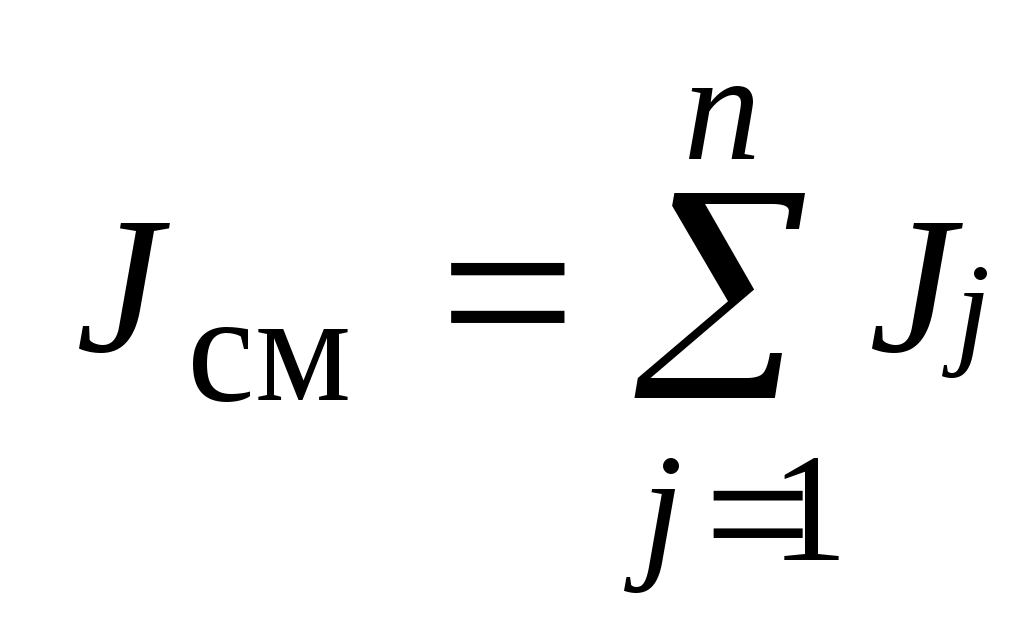 , ,
где:  - энтальпия - энтальпия 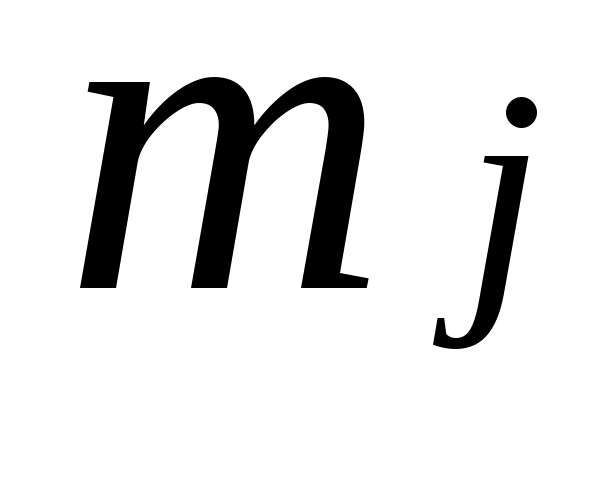 килограммов i- го газа в составе смеси; килограммов i- го газа в составе смеси;
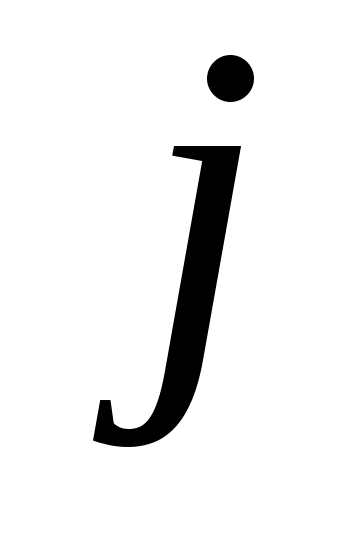 = 1, 2, .........., = 1, 2, .........., 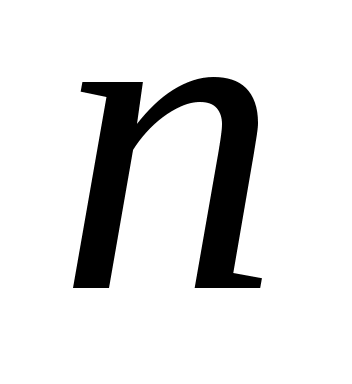 . .
(В формулах для вычисления энтальпии индекс «i» для газа заменен на «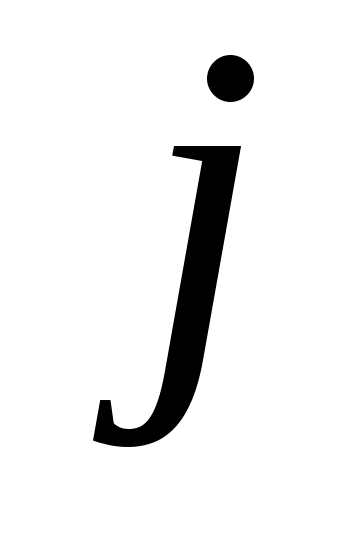 » во избежание совпадения обозначений удельной энтальпии (i) и индекса i-го газа) » во избежание совпадения обозначений удельной энтальпии (i) и индекса i-го газа)
По аналогии с внутренней энергией можно получить формулу для удельной энтальпии смеси газов iсм , Дж / кг:
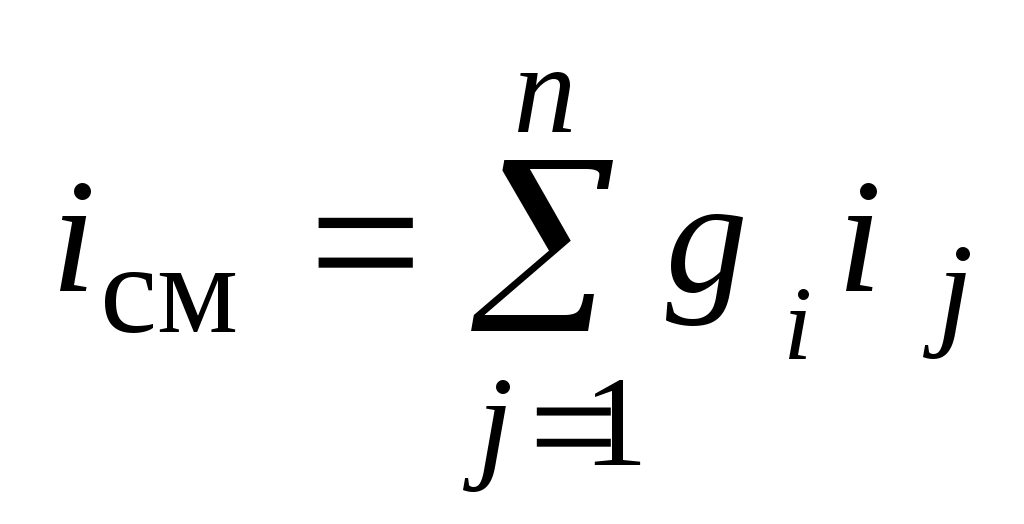 , ,
где: 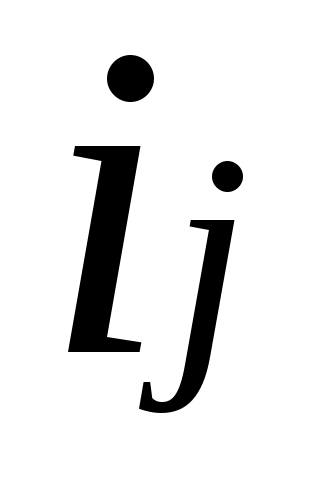 - удельная энтальпия i-го газа в составе смеси. - удельная энтальпия i-го газа в составе смеси.
Пример 4.
Все термодинамические функции состояния смеси газов также обладают свойством аддитивности.
К функциям состояния помимо всех характеристических функций (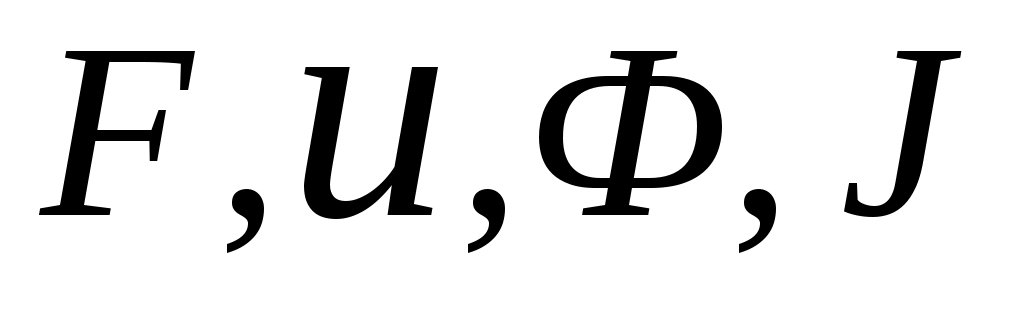 ) относится также энтропия ) относится также энтропия 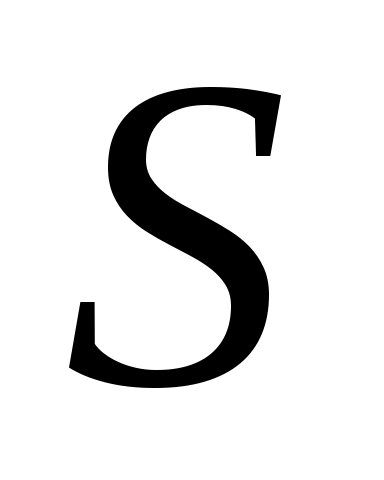 - термодинамический параметр состояния. - термодинамический параметр состояния.
Здесь: 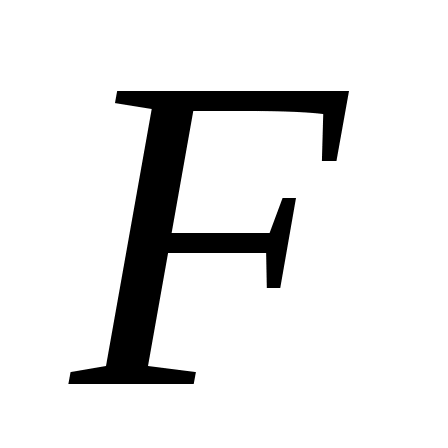 - свободная энергия (энергия Гельмгольца, изохорно-изотерми- ческий потенциал), Дж - свободная энергия (энергия Гельмгольца, изохорно-изотерми- ческий потенциал), Дж
 - свободная энтальпия (энтальпия Гиббса, изобарный потенциал, изобарно-изотермический потенциал), Дж. - свободная энтальпия (энтальпия Гиббса, изобарный потенциал, изобарно-изотермический потенциал), Дж.
Для свободной энергии 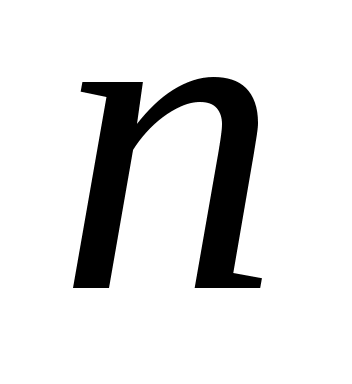 -компонентной смеси газов массой -компонентной смеси газов массой 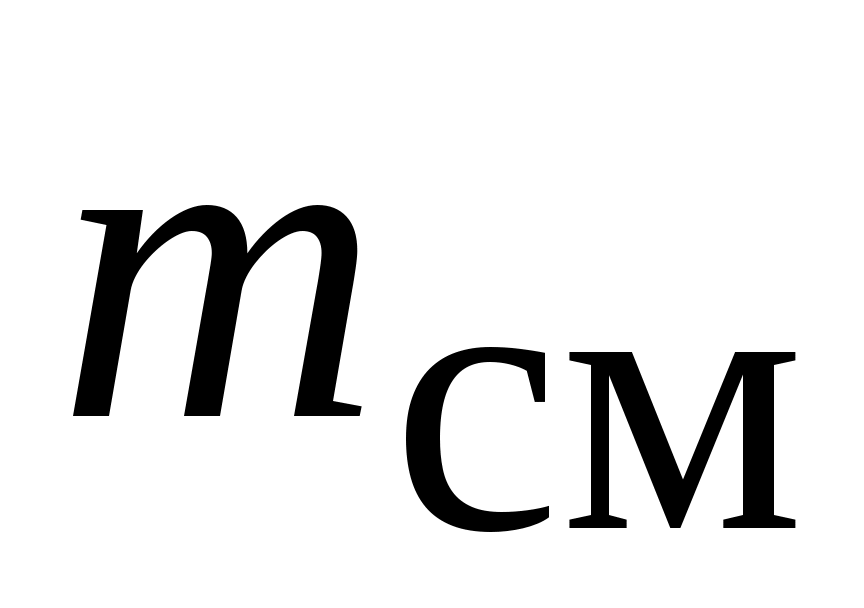 по аналогии с внутренней энергией и энтальпией смеси можно окончательно записать: по аналогии с внутренней энергией и энтальпией смеси можно окончательно записать:
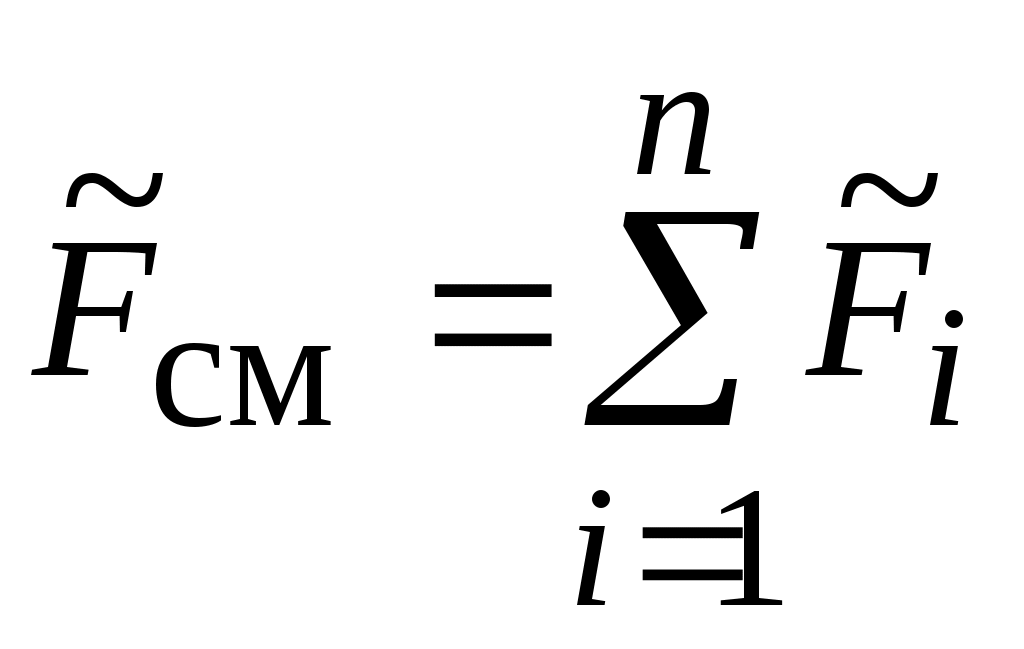 , ,
Здесь: 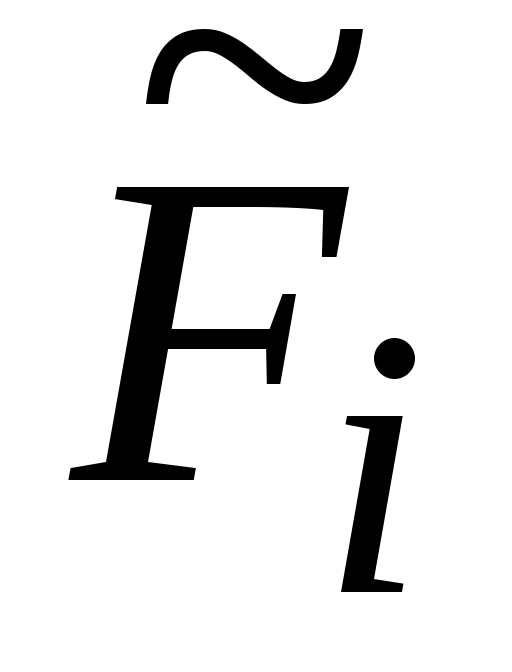 - свободная энергия i-го газа массой - свободная энергия i-го газа массой 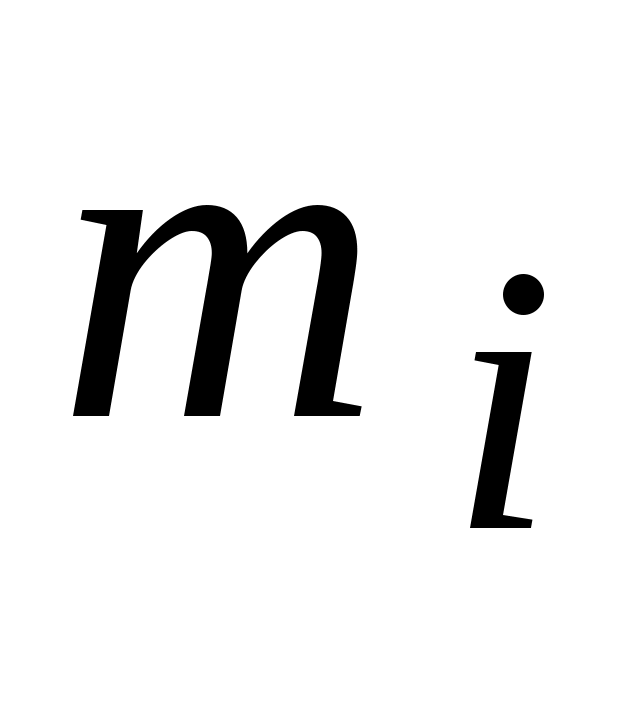 в составе смеси, Дж. в составе смеси, Дж.
(Знак “ ” («тильда») над буквой 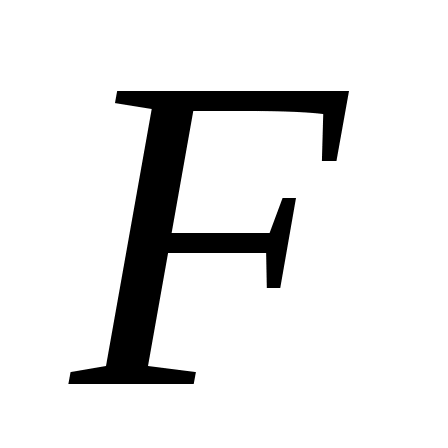 в данном случае использован для того, чтобы в дальнейшем не менять общепринятое обозначение в данном случае использован для того, чтобы в дальнейшем не менять общепринятое обозначение 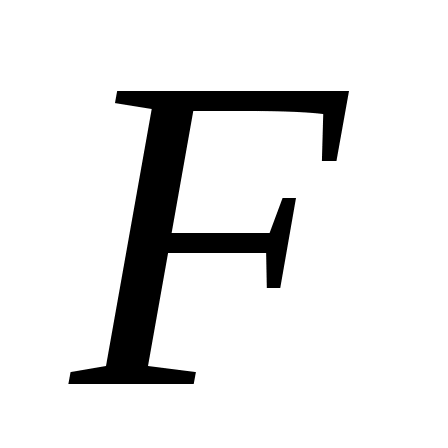 для удельной свободной энергии газа). для удельной свободной энергии газа).
Fсм- удельная свободная энергия смеси газов, Дж / кг:
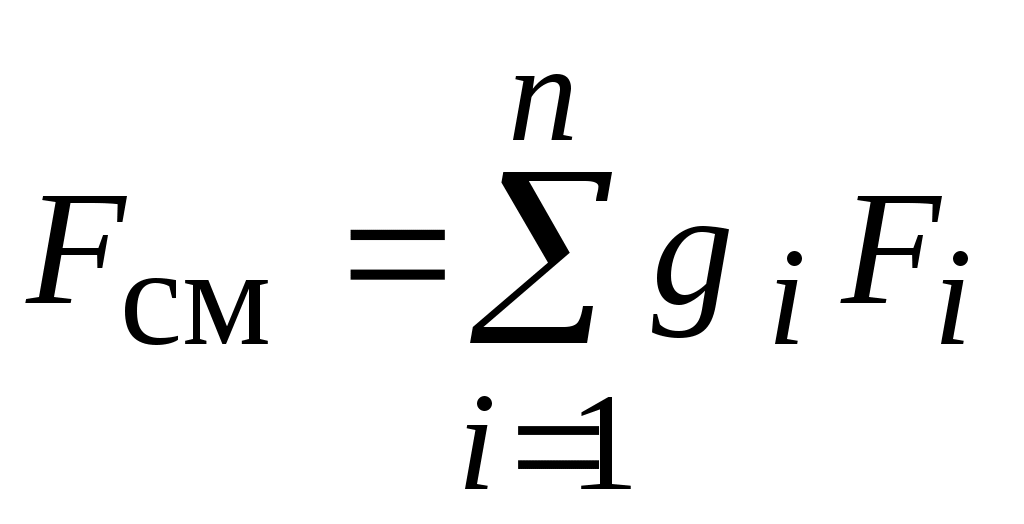 , ,
где: 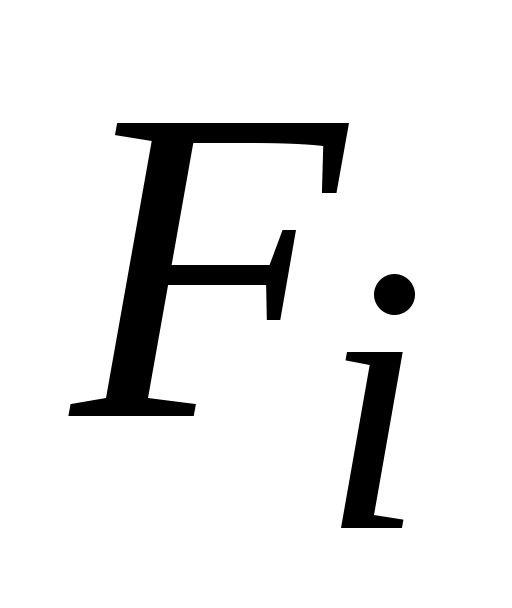 - удельная свободная энергия i-го газа смеси, Дж / кг. - удельная свободная энергия i-го газа смеси, Дж / кг.
Пример 5
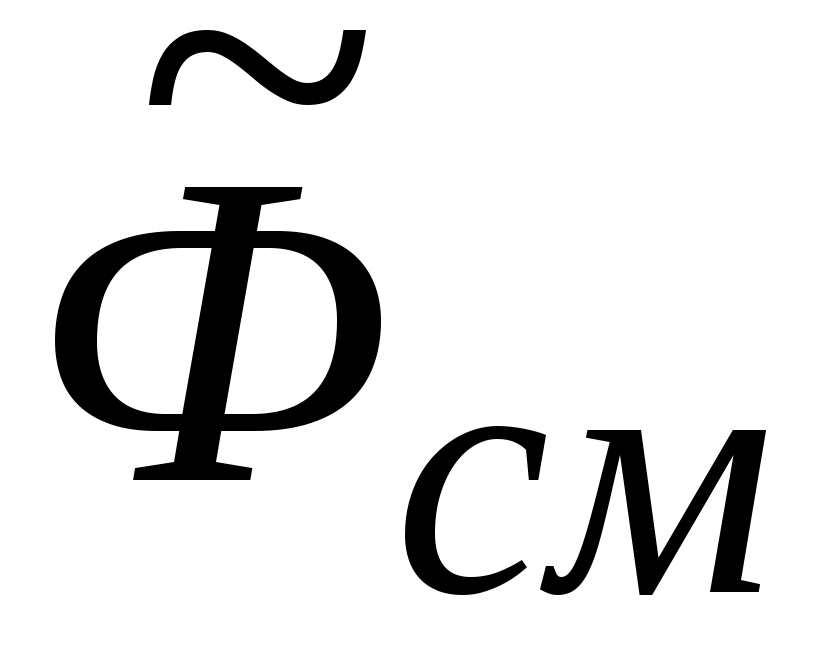 - свободная энтальпия всей массы mсм - свободная энтальпия всей массы mсм 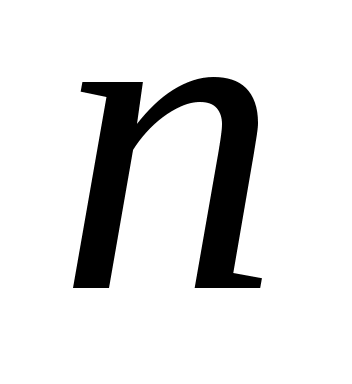 -компонентной смеси газов, Дж: -компонентной смеси газов, Дж:
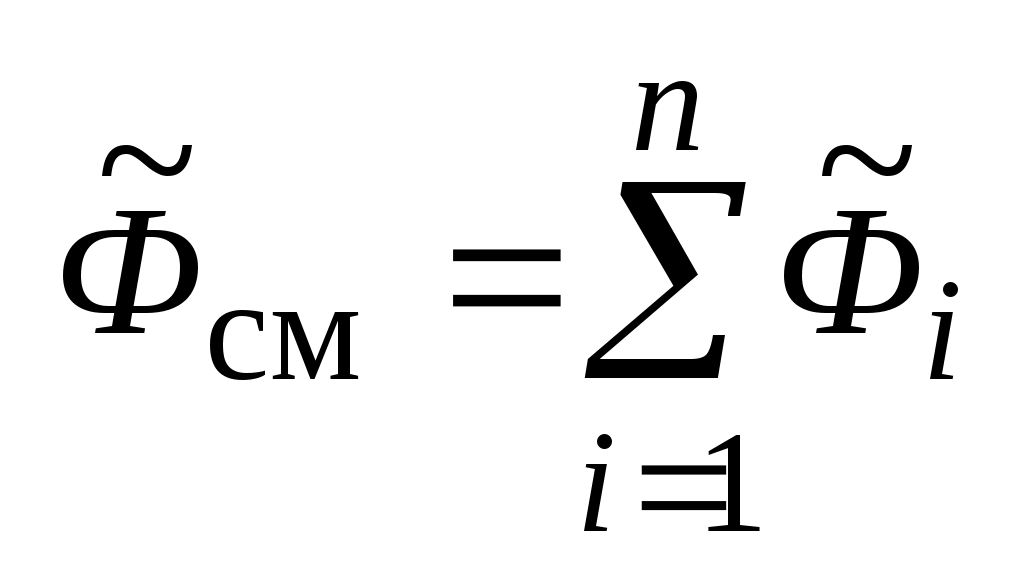 , ,
где: 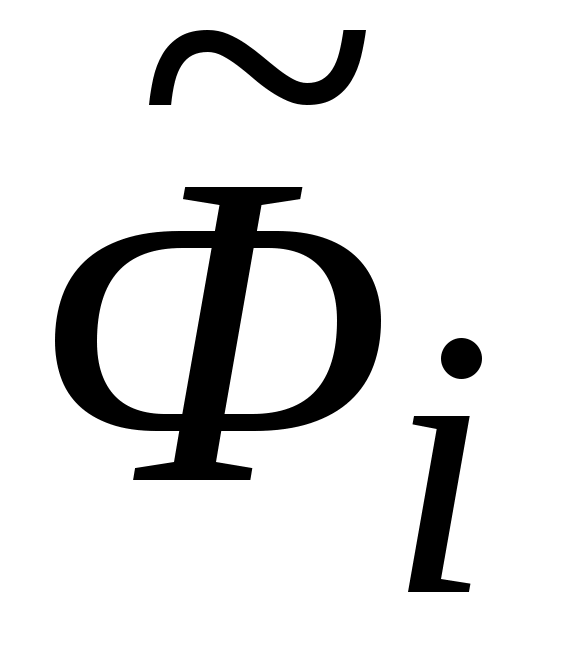 - свободная энергия i-го газа массой - свободная энергия i-го газа массой 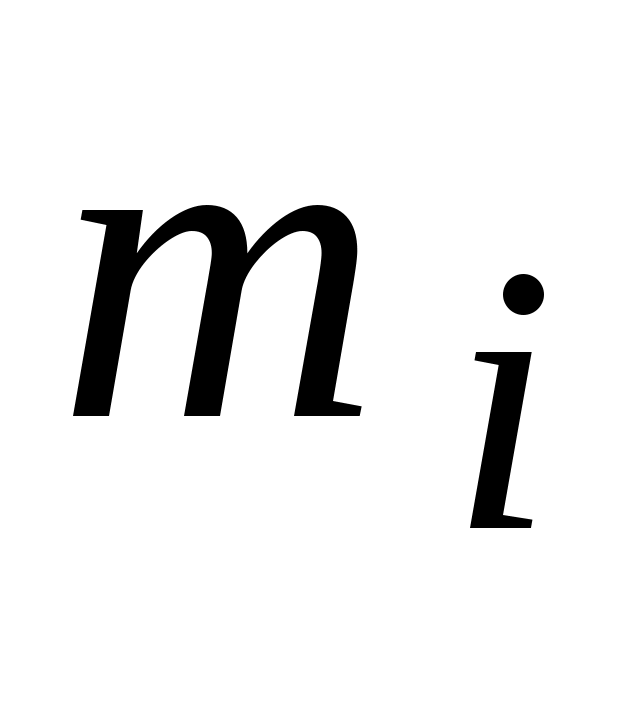 в составе смеси, Дж; в составе смеси, Дж;
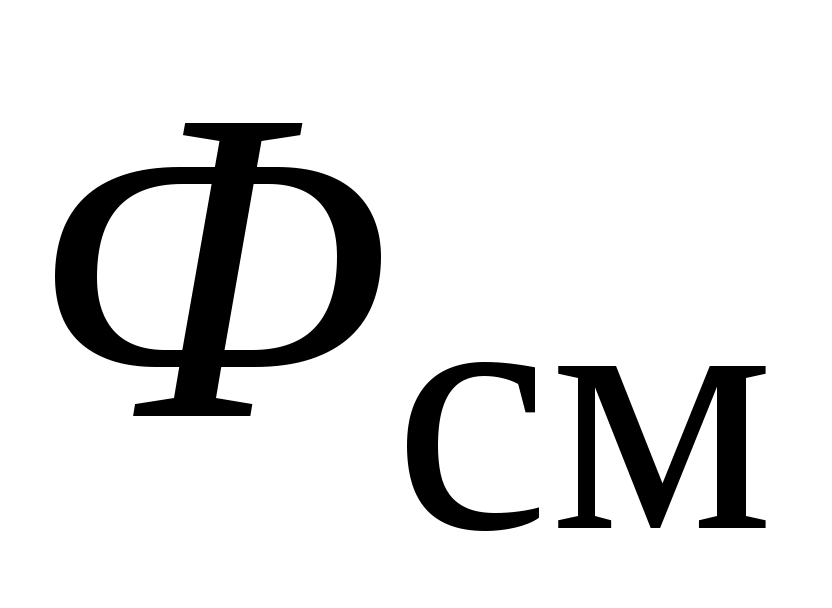 - удельная свободная энергия смеси газов, Дж / кг: - удельная свободная энергия смеси газов, Дж / кг:
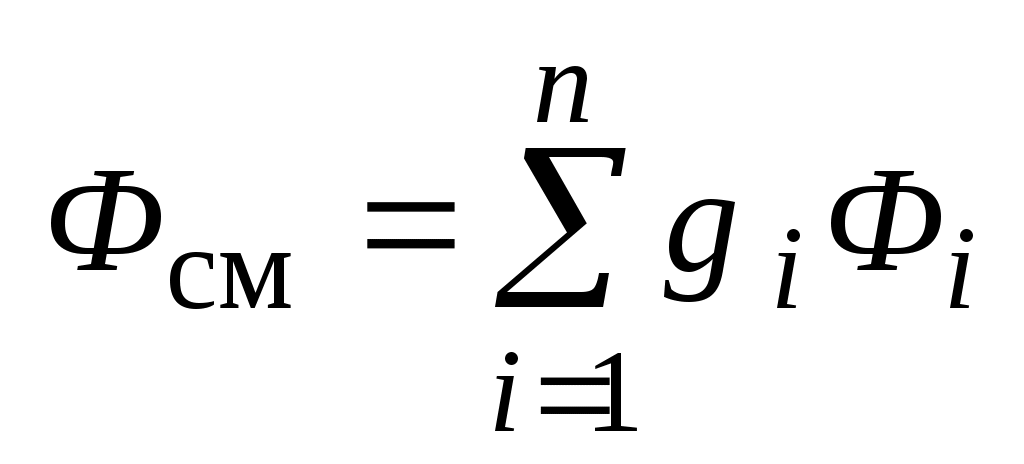 , ,
где: 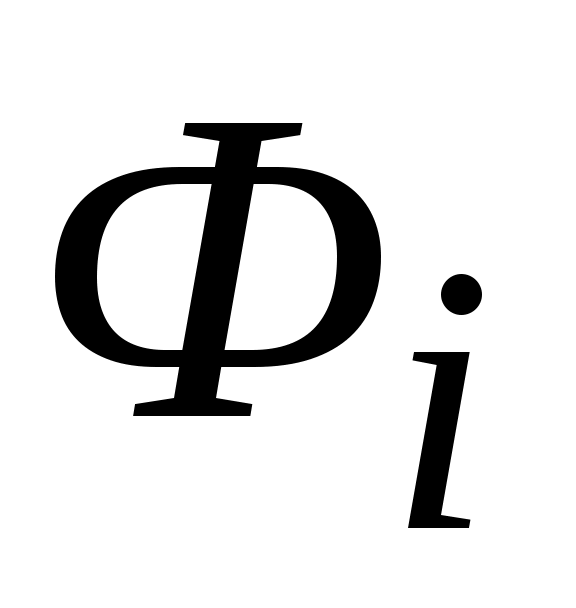 - удельная свободная энергия i-го газа смеси, Дж / кг - удельная свободная энергия i-го газа смеси, Дж / кг
Пример 6
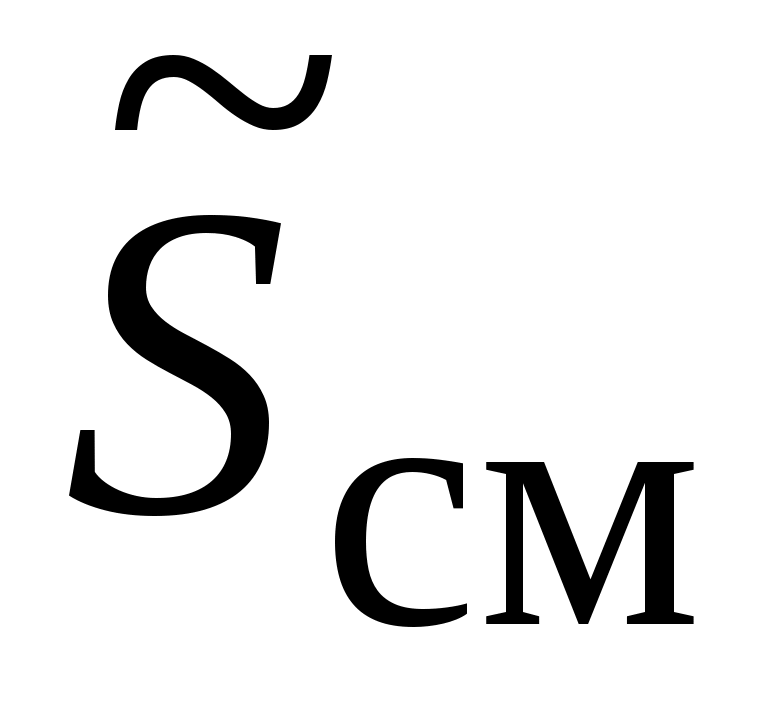 - энтропия - энтропия 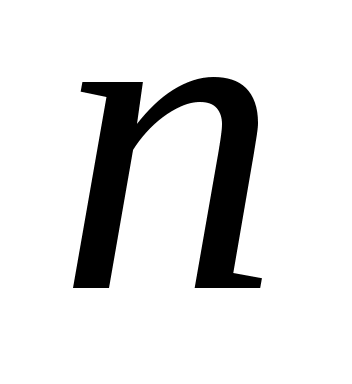 -компонентной смеси с общей массой -компонентной смеси с общей массой 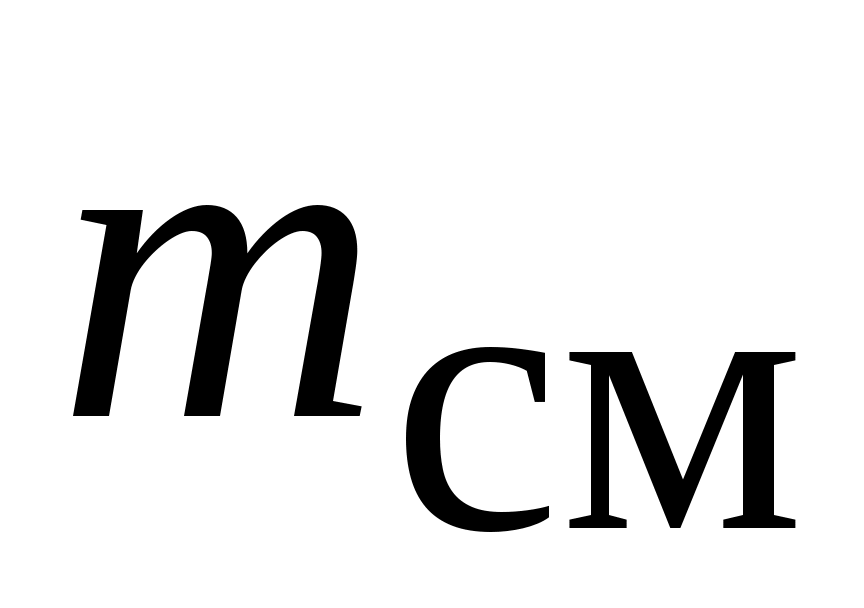 , Дж / К: , Дж / К:
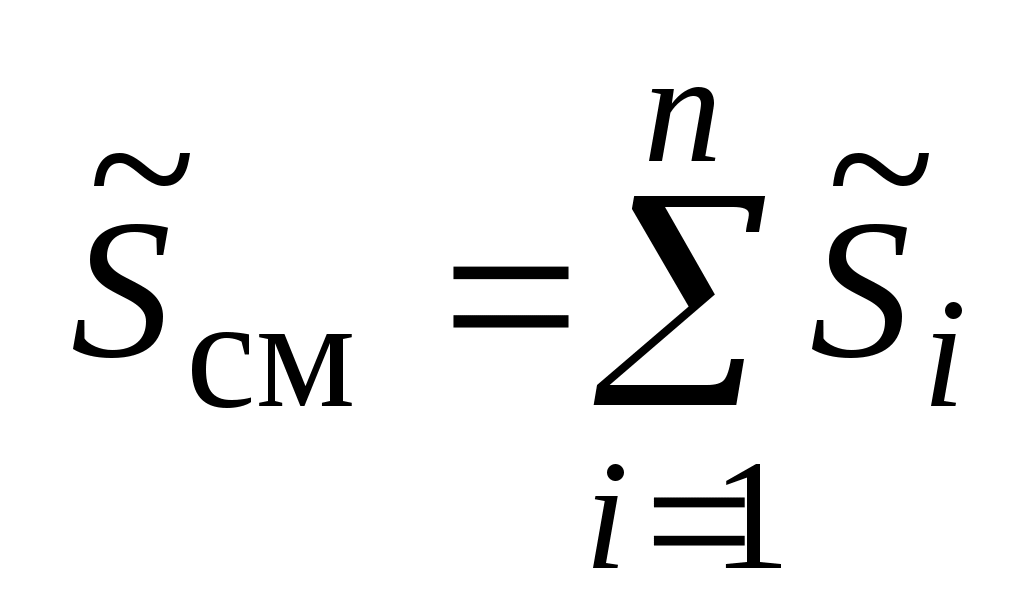 , ,
где: 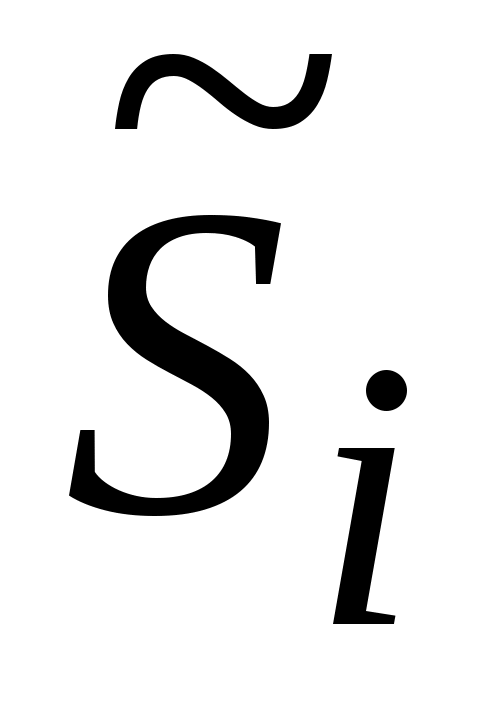 - энтропия i-го газа массой - энтропия i-го газа массой 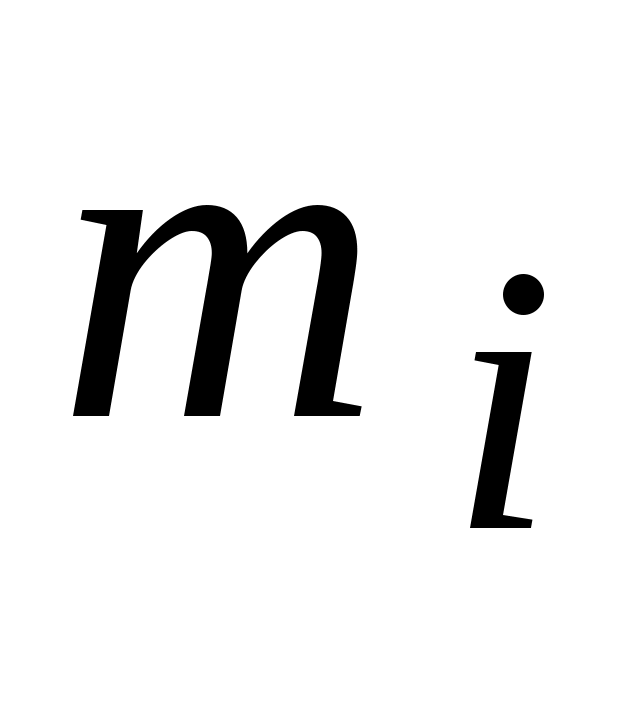 в составе смеси, Дж / кг. в составе смеси, Дж / кг.
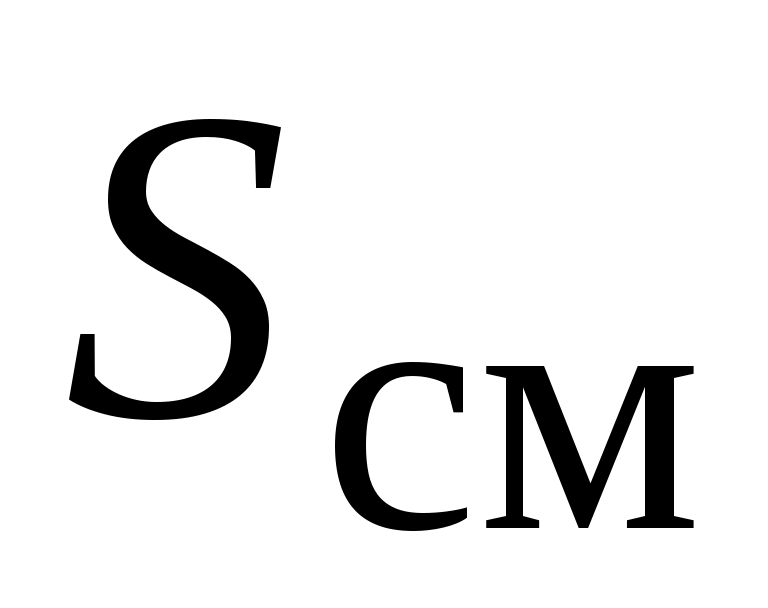 - удельная энтропия смеси газов, Дж / (кгК) - удельная энтропия смеси газов, Дж / (кгК)
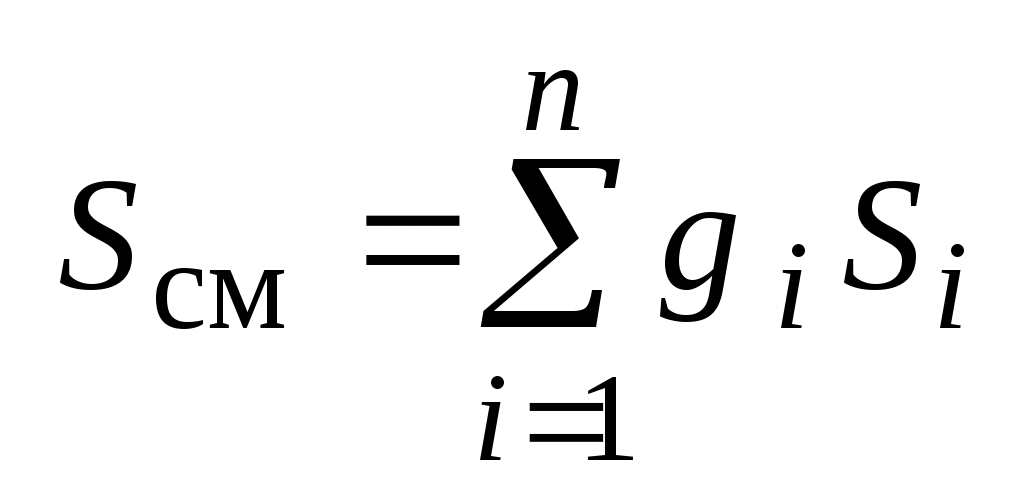 , ,
где: 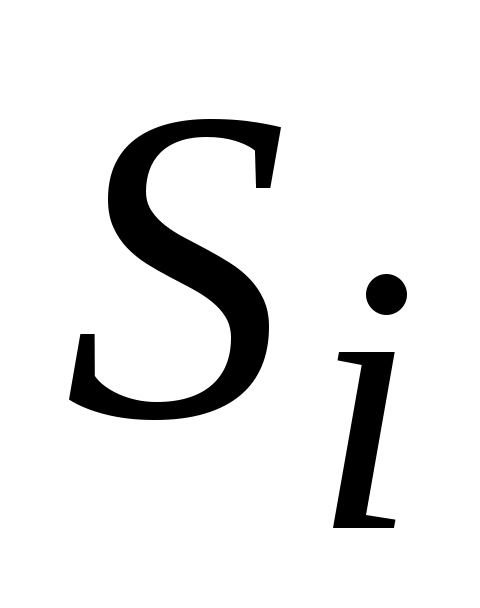 - удельная энтропия i-го газа смеси, Дж / (кгК) - удельная энтропия i-го газа смеси, Дж / (кгК)
1.4.1.2. Мольные значения функций и параметров смеси газов
Переход от удельных значений к мольным значениям рассмотрим на примере внутренней энергии.
От единиц измерения количества вещества внутренняя энергия смеси  не зависит, поэтому не зависит, поэтому  - это одна и та же величина как для - это одна и та же величина как для 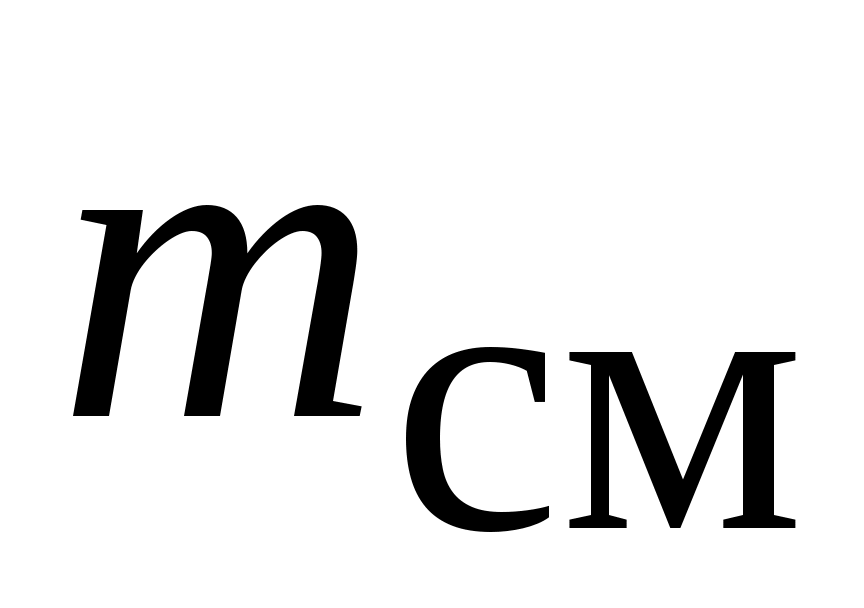 килограммов смеси, так и для килограммов смеси, так и для 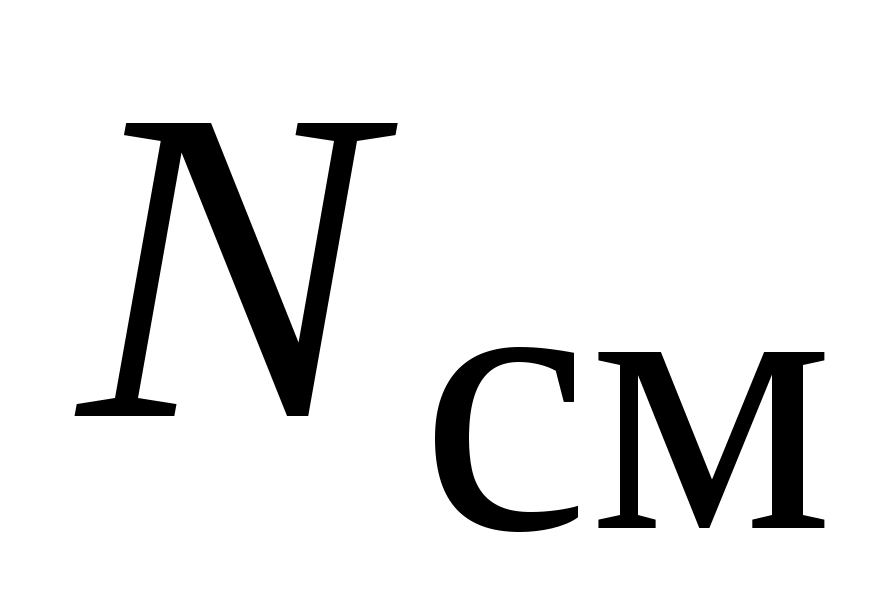 киломолей этой же киломолей этой же 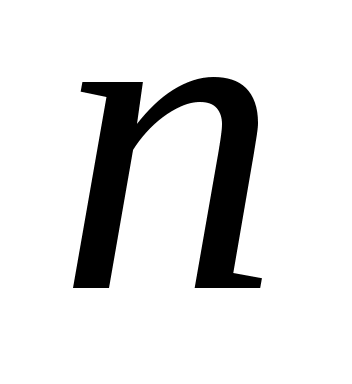 -компонентной смеси, занимающий объем -компонентной смеси, занимающий объем  при температуре при температуре 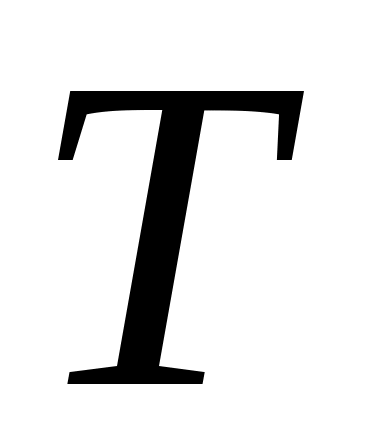 и давлении и давлении 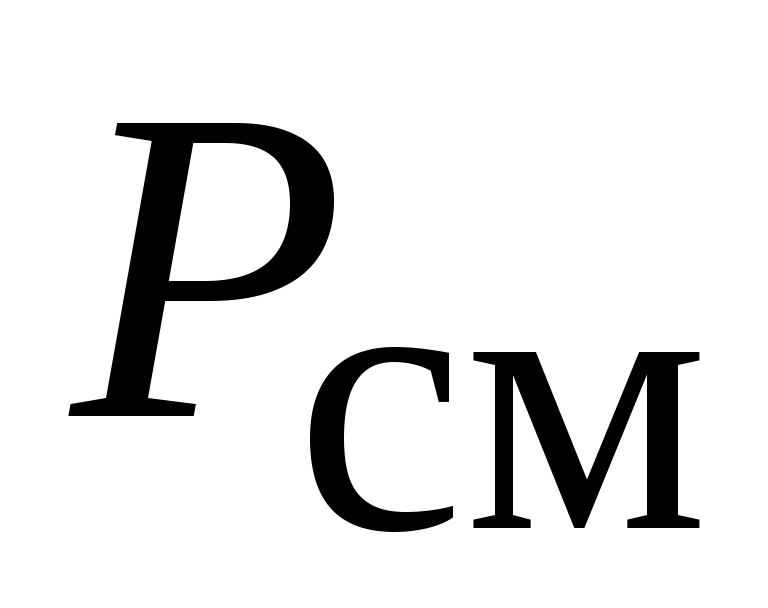 . .
Аналогично, 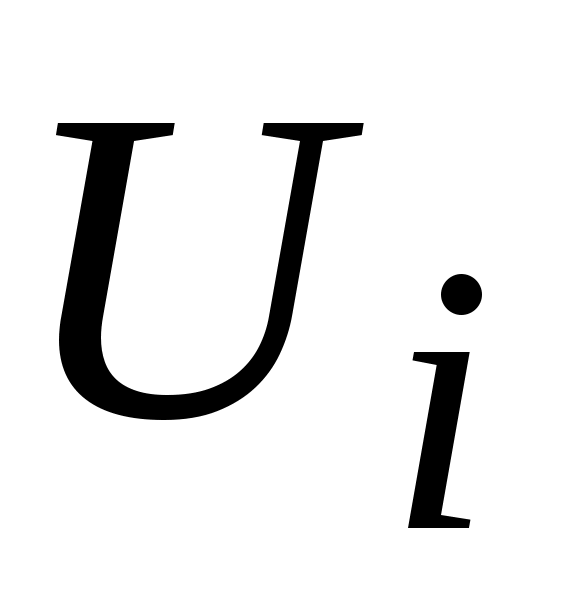 - внутренняя энергия - внутренняя энергия 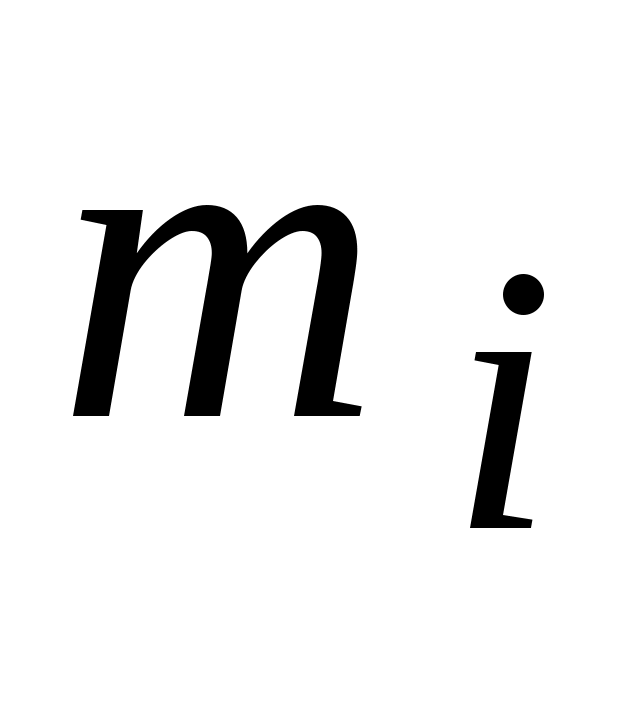 килограммов или килограммов или 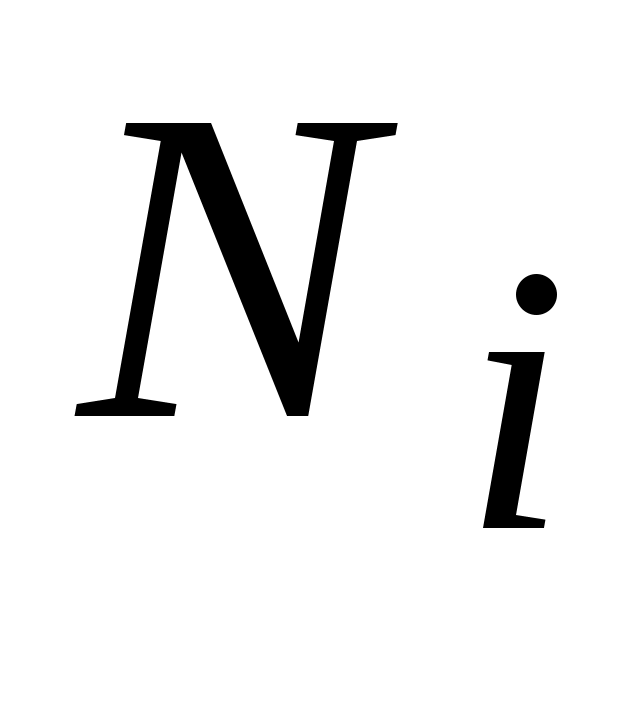 - киломолей i-го газа в составе смеси. - киломолей i-го газа в составе смеси.
Из свойства аддитивности количества вещества смеси следует:
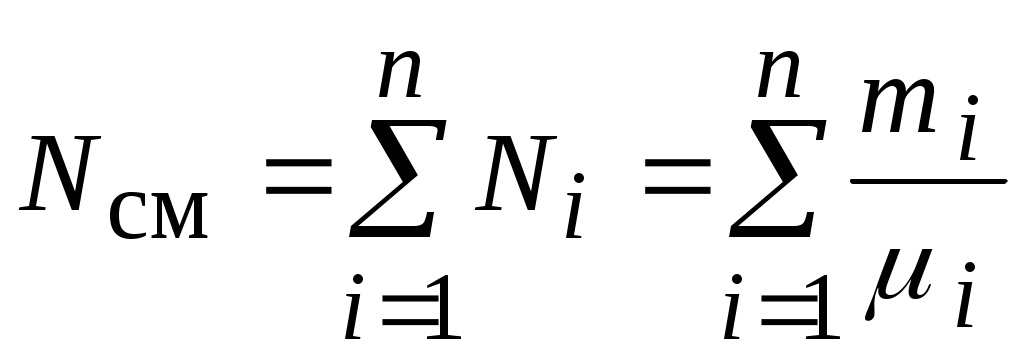
Ранее было получено, что
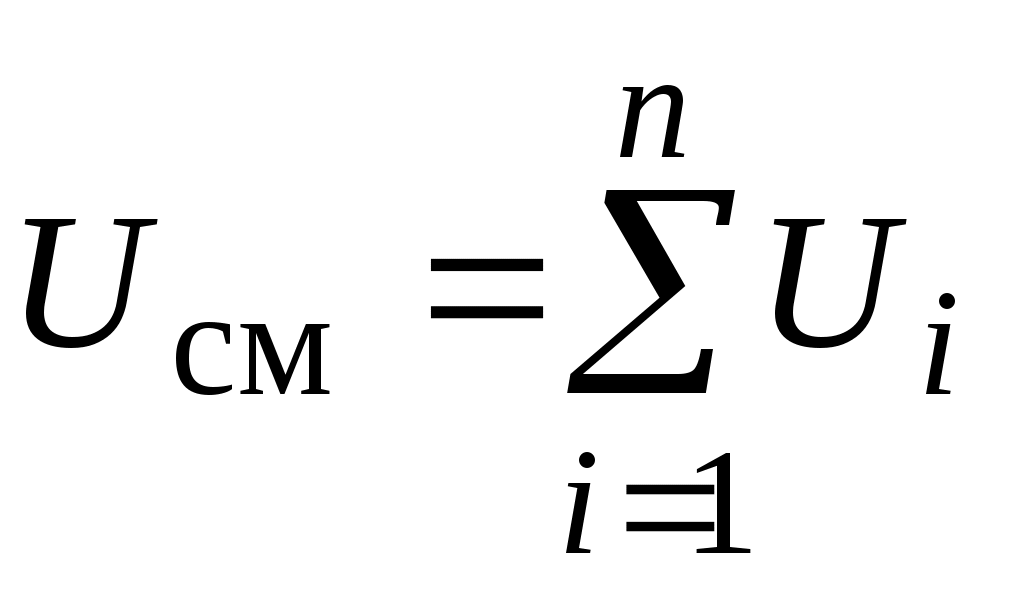 . .
Разделим обе части этого равенства на общее количество киломолей смеси 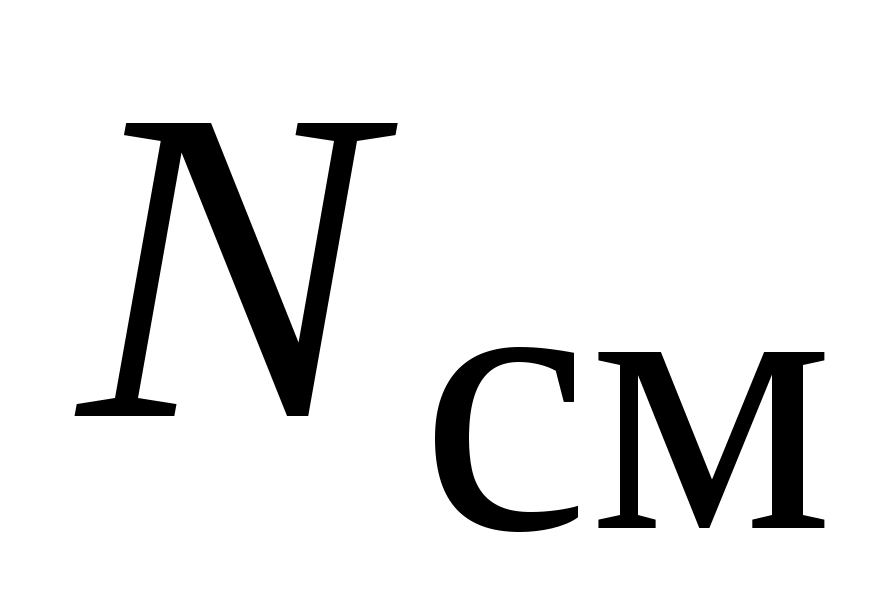 и введем обозначения: и введем обозначения:
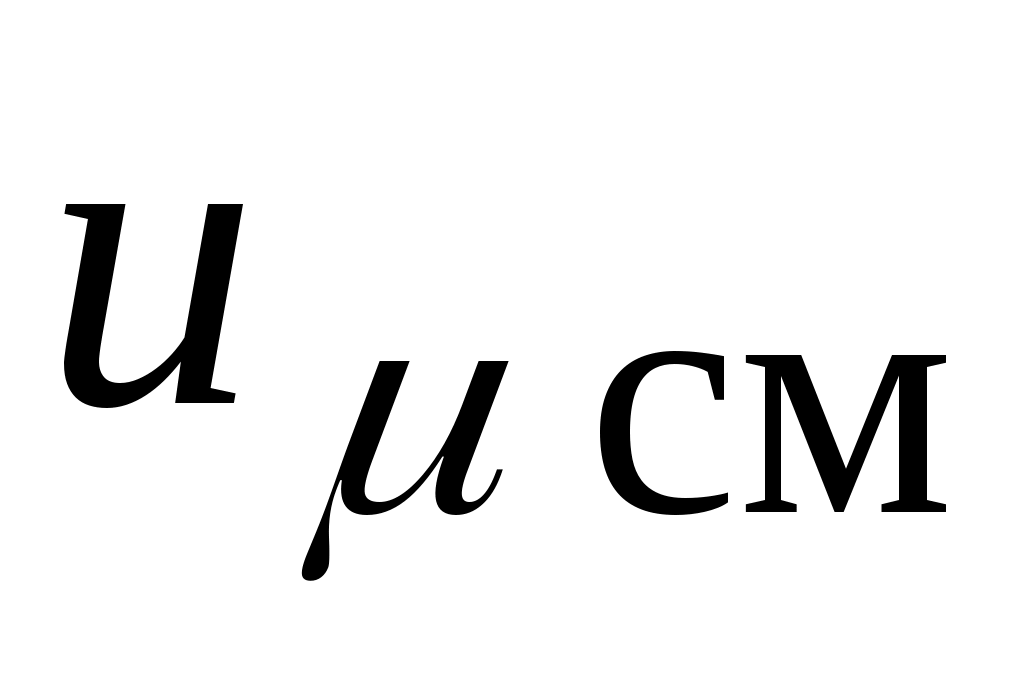 - мольная внутренняя энергия (внутренняя энергия одного киломоля) смеси газов, Дж / кмоль: - мольная внутренняя энергия (внутренняя энергия одного киломоля) смеси газов, Дж / кмоль:
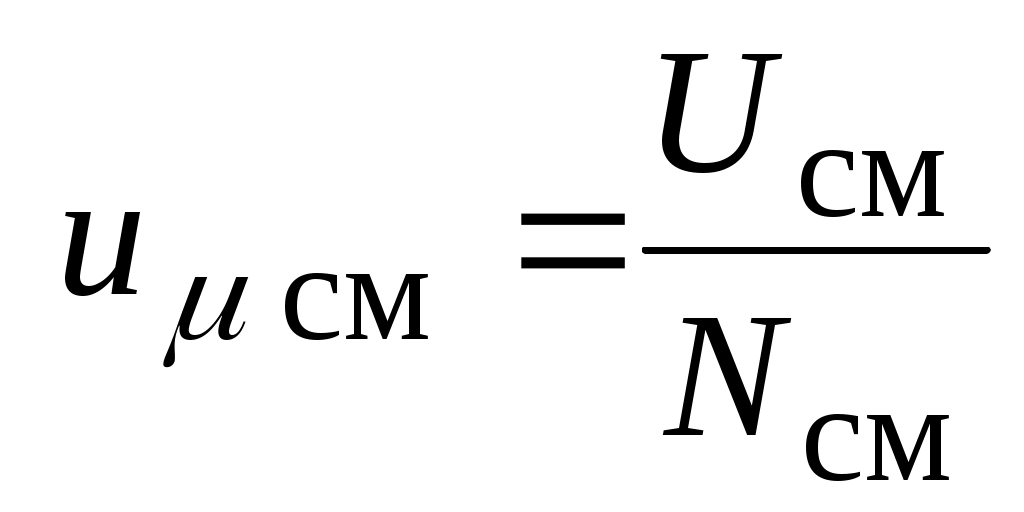 . .
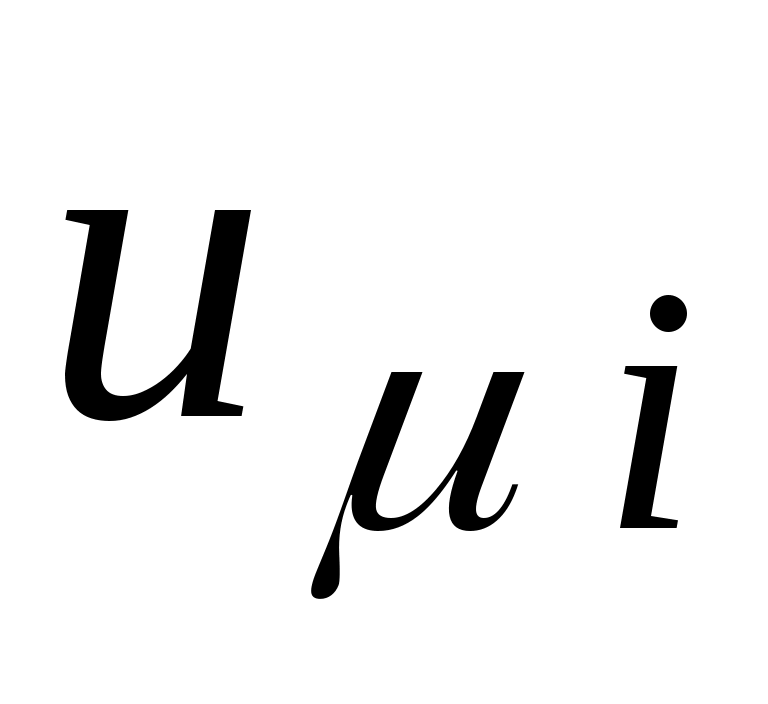 - мольная внутренняя энергия i-го газа, Дж / кмоль: - мольная внутренняя энергия i-го газа, Дж / кмоль:
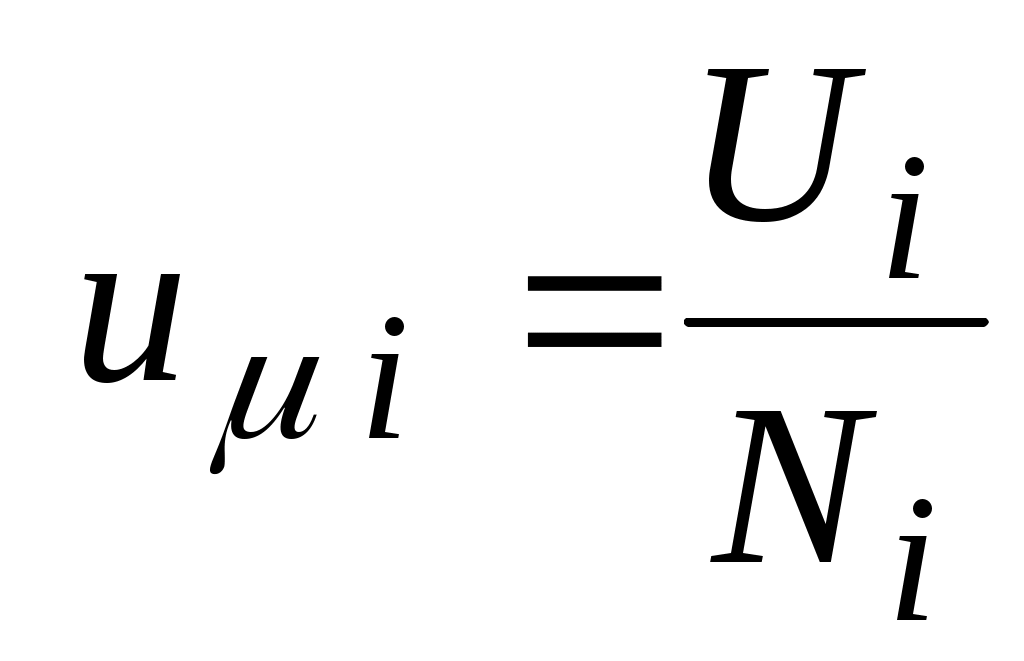 . .
Тогда 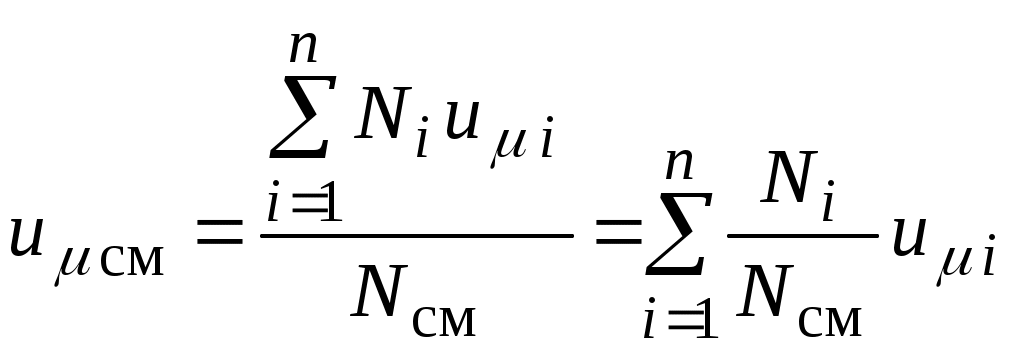
По определению 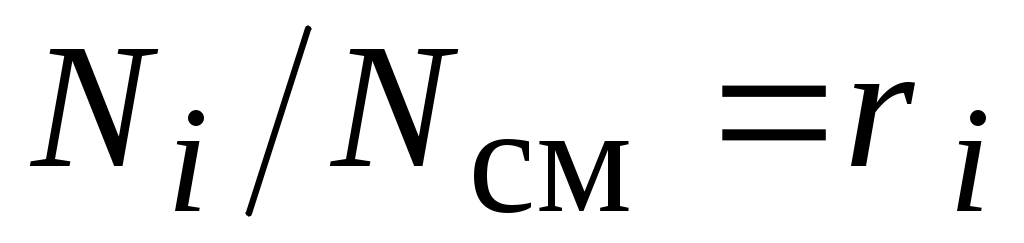 , поэтому окончательно мольная внутренняя энергия смеси газов, Дж / кмоль: , поэтому окончательно мольная внутренняя энергия смеси газов, Дж / кмоль:
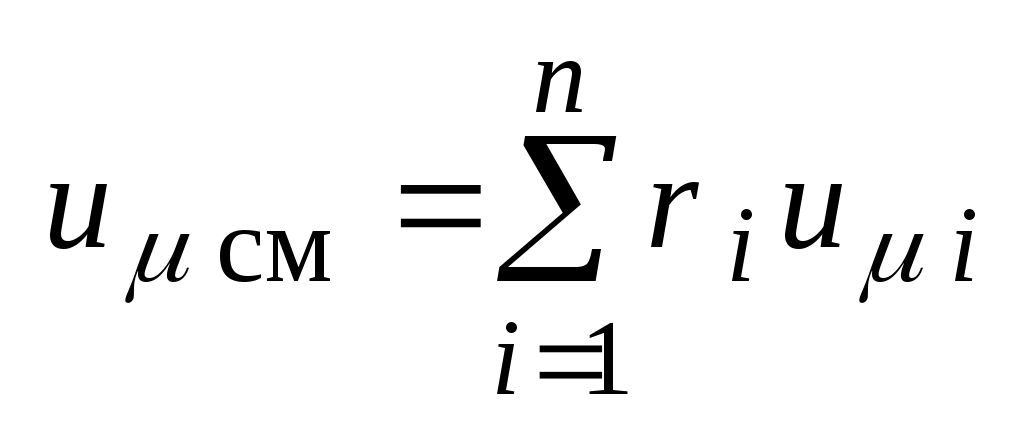 . .
Далее по аналогии:
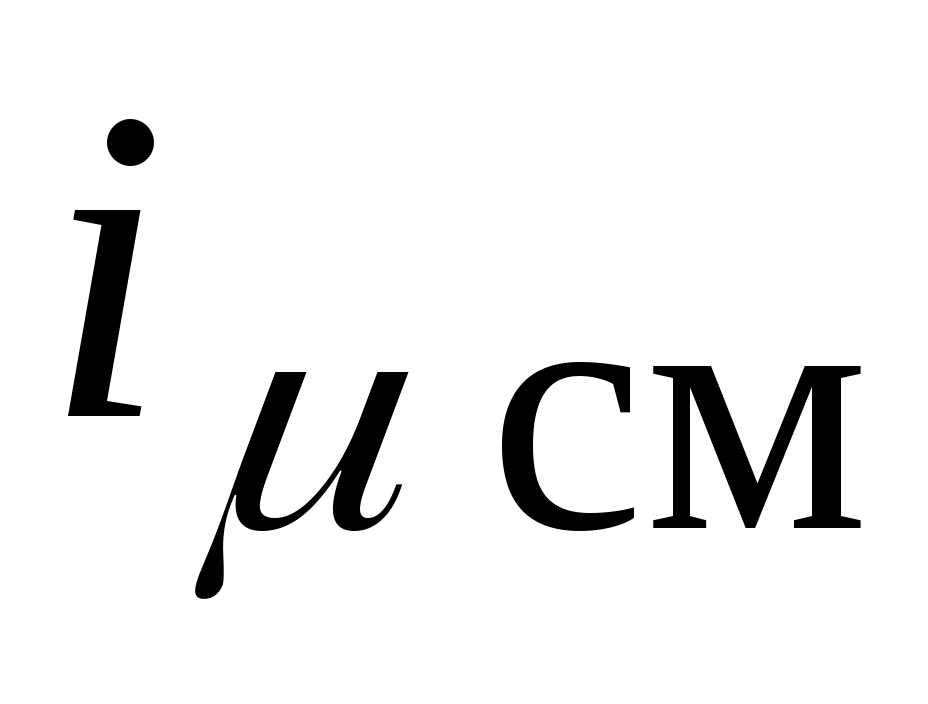 - мольная энтальпия смеси, Дж / кмоль: - мольная энтальпия смеси, Дж / кмоль:
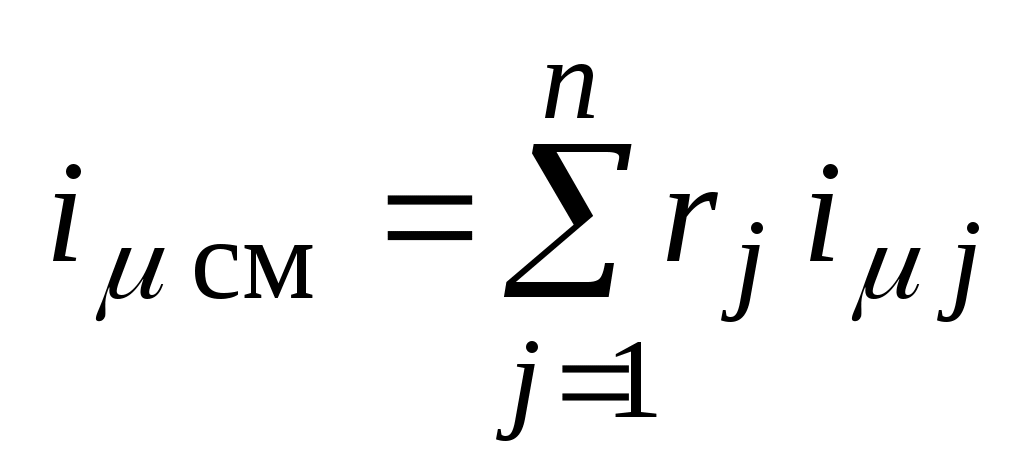 , ,
где: 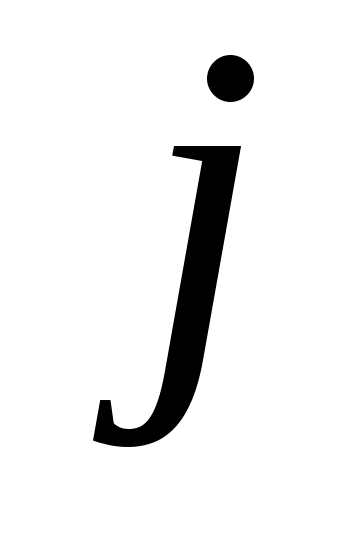 = 1, 2, ....... = 1, 2, ....... 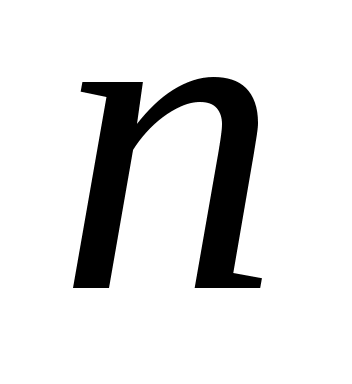 ; ;
 - мольная энтальпия - мольная энтальпия 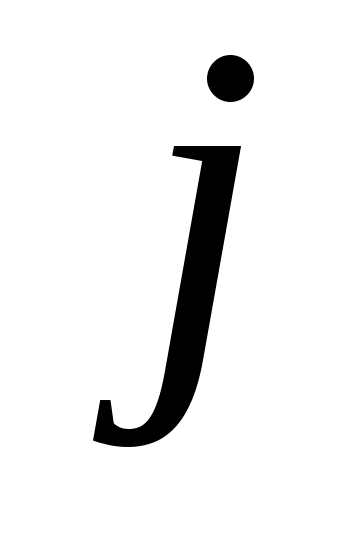 -го газа, Дж / кмоль. -го газа, Дж / кмоль.
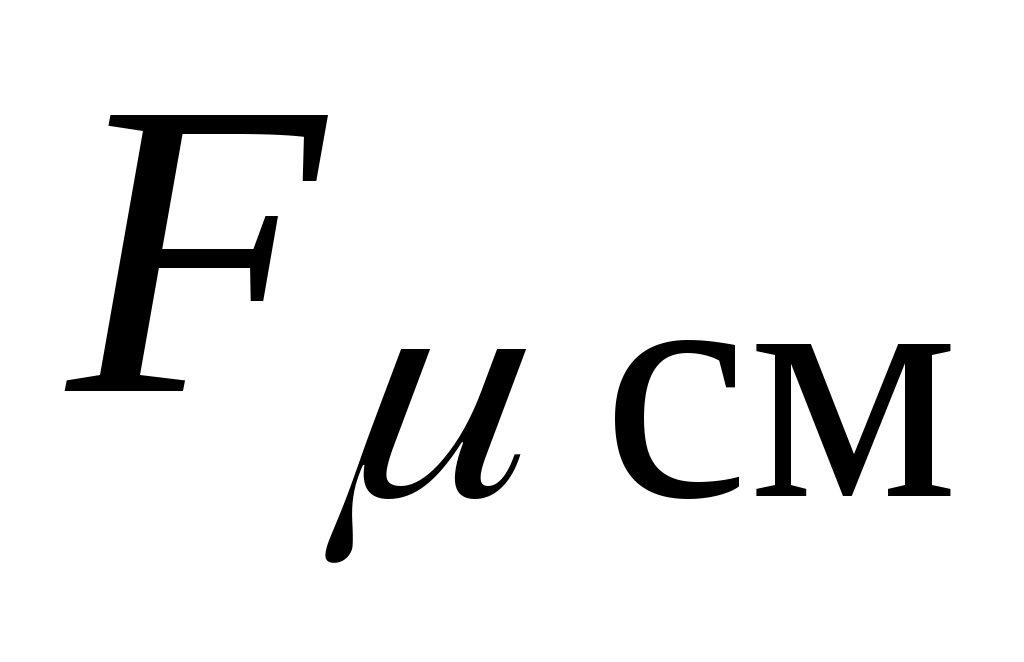 - мольная свободная энергия смеси, Дж / кмоль: - мольная свободная энергия смеси, Дж / кмоль:
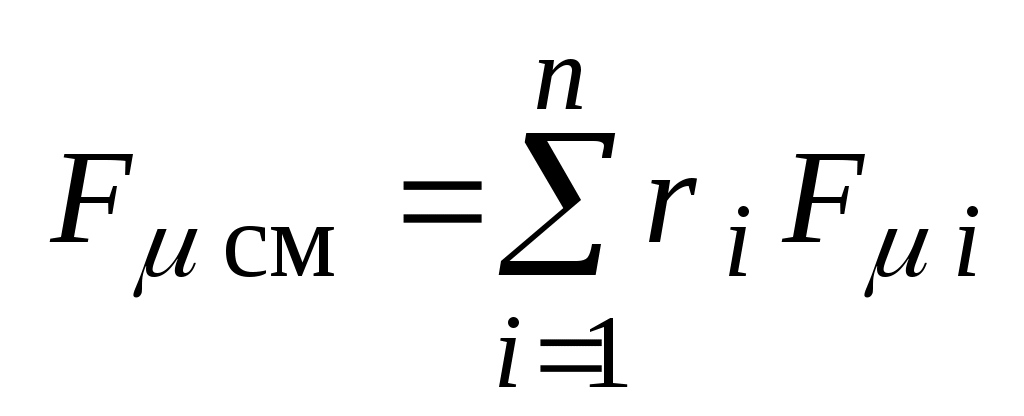 . .
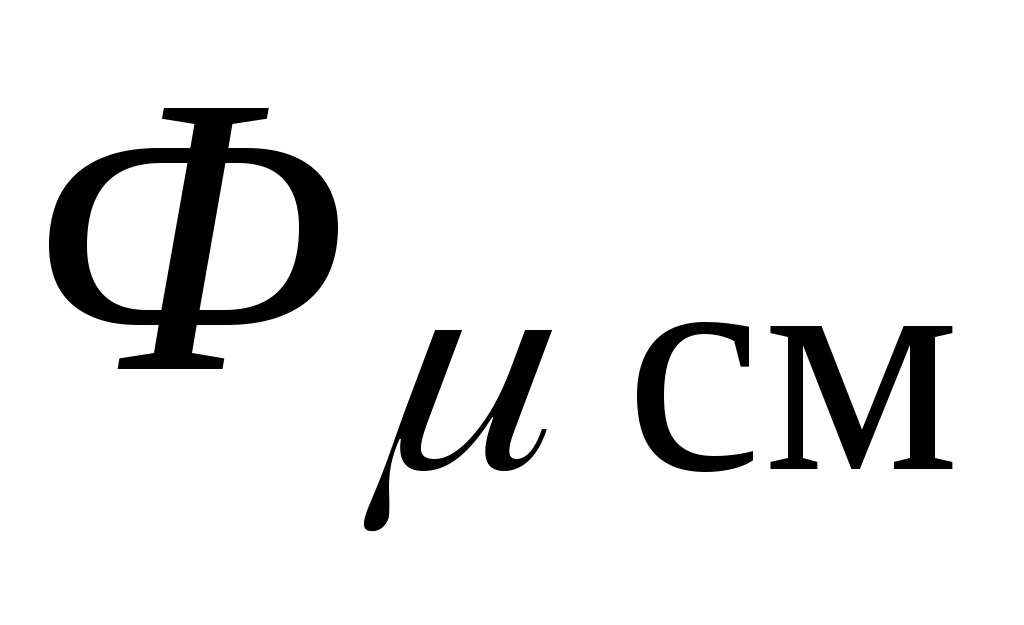 - мольная свободная энтальпия смеси, Дж / кмоль: - мольная свободная энтальпия смеси, Дж / кмоль:
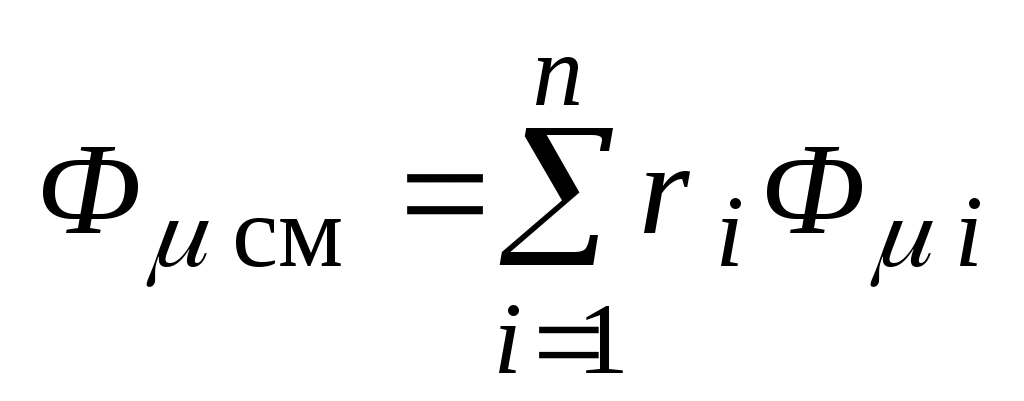 . .
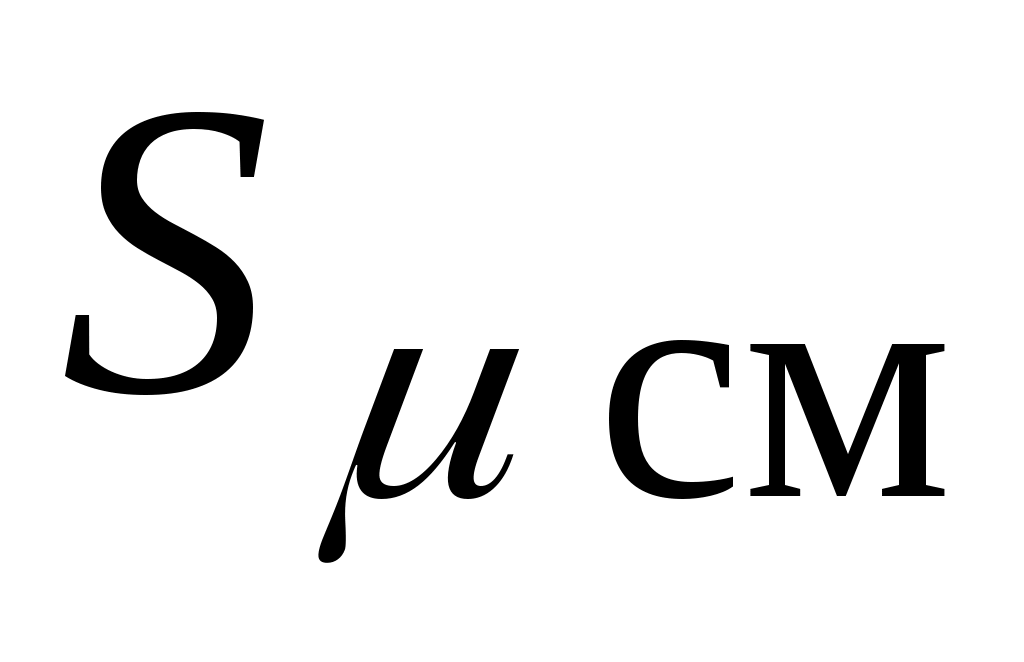 - мольная энтропия смеси, Дж / (кмольК): - мольная энтропия смеси, Дж / (кмольК):
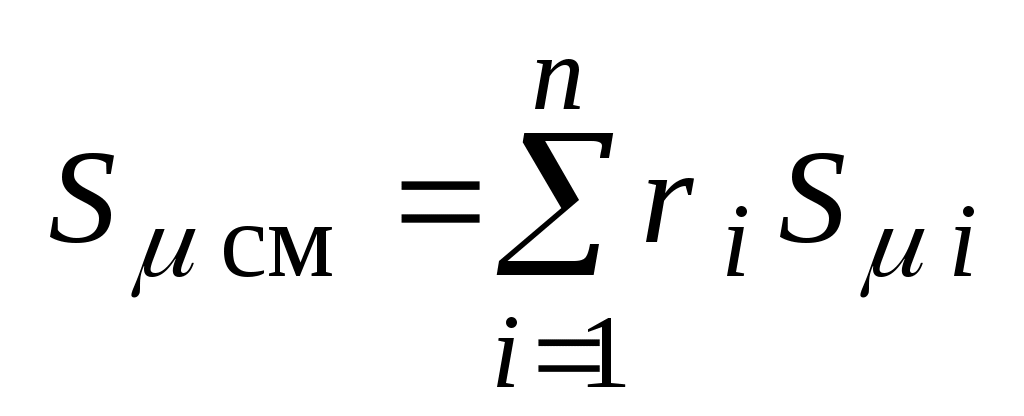 . .
Здесь 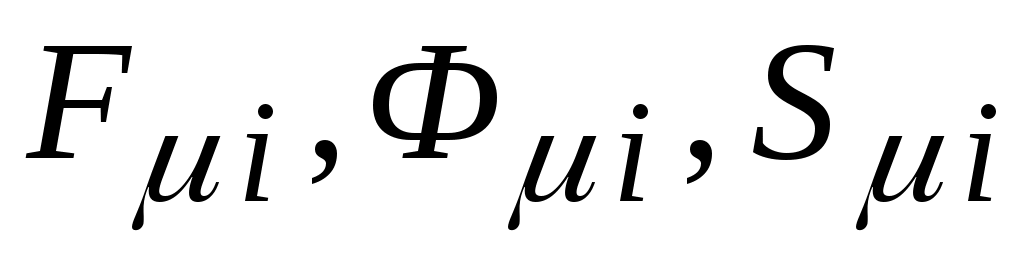 - мольные значения соответственно свободной энергии, свободной энтальпии и энтропии i-го газа в составе смеси. - мольные значения соответственно свободной энергии, свободной энтальпии и энтропии i-го газа в составе смеси.
1.4.2. Парциальное давление.
Давление и объем смеси идеальных газов также являются аддитивными величинами, поэтому
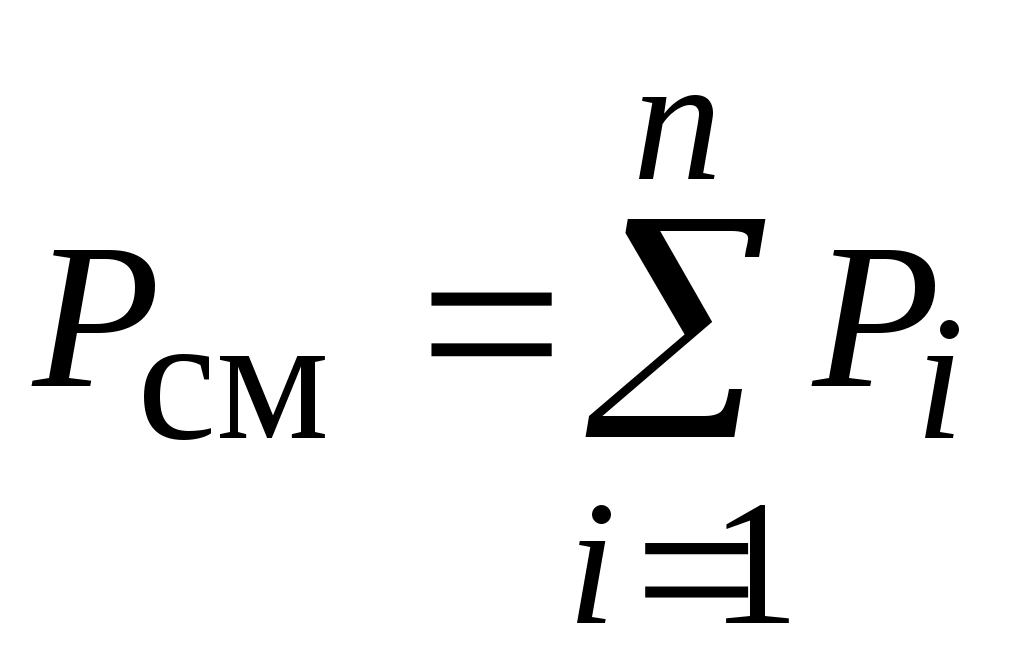 и и 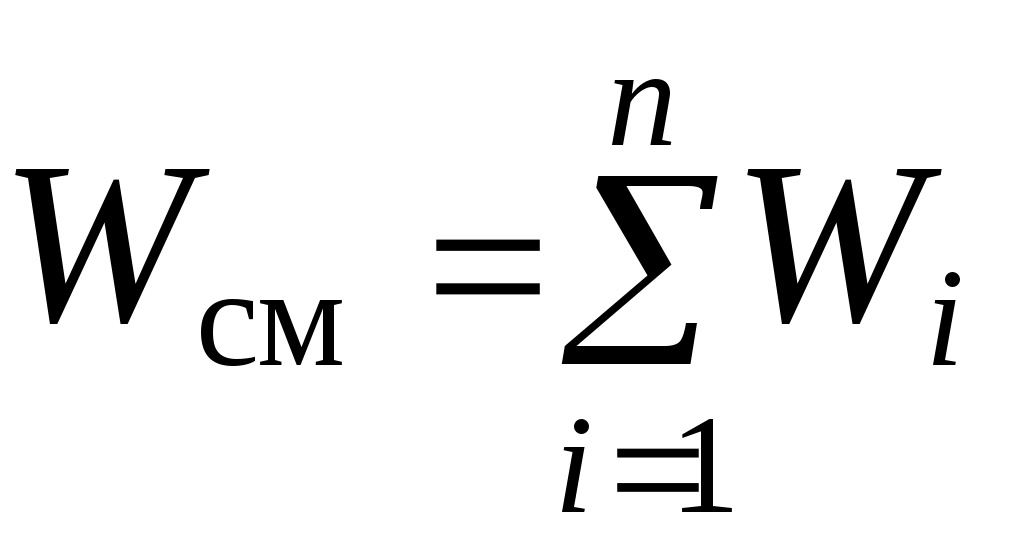 , ,
где: Рi – парциальное давление,
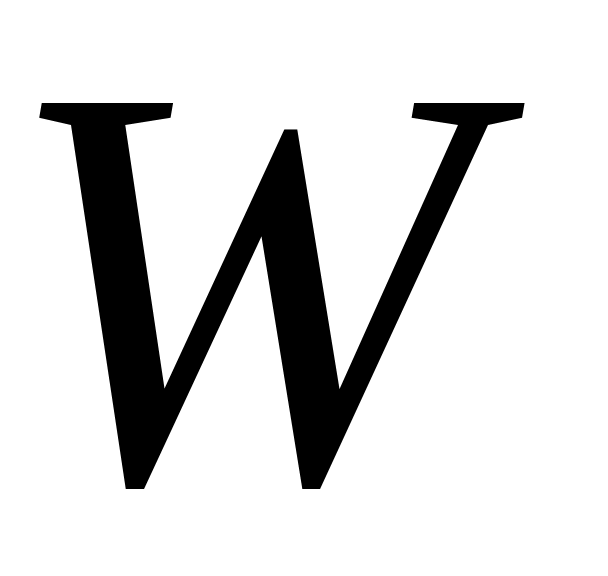 i – парциальный объем. i – парциальный объем.
Каждый из идеальных газов смеси, находясь в объеме  и при температуре смеси и при температуре смеси 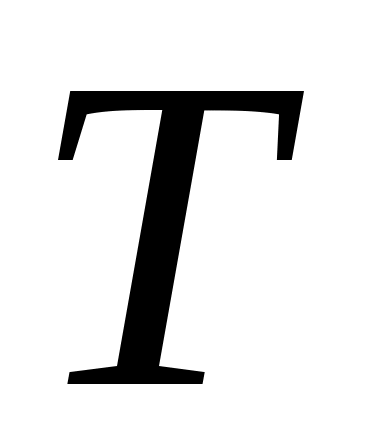 , отдельно и независимо от других создает некоторое давление , отдельно и независимо от других создает некоторое давление 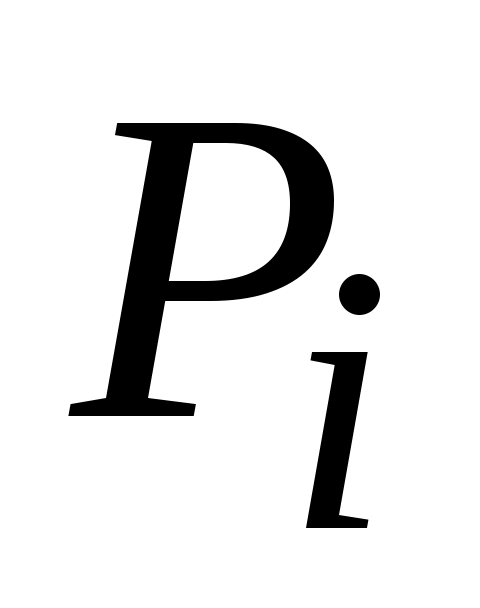 , называемое парциальным давлением. , называемое парциальным давлением.
(Термин « парциальный » происходит от латинского partialis - частичный, отдельный)
Коротко остановимся на физическом смысле парциального давления.
Если смесь газов находится в равновесии, то все газы имеют одинаковую температуру 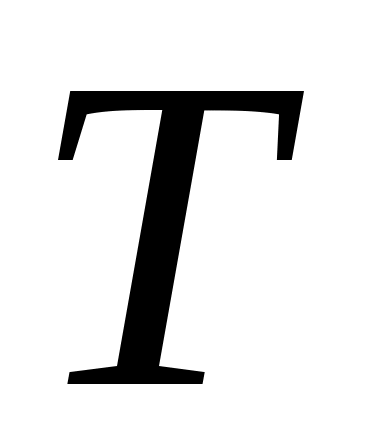 , а их молекулы равномерно распределены по всему объему смеси. , а их молекулы равномерно распределены по всему объему смеси.
Уравнение состояния идеального газа 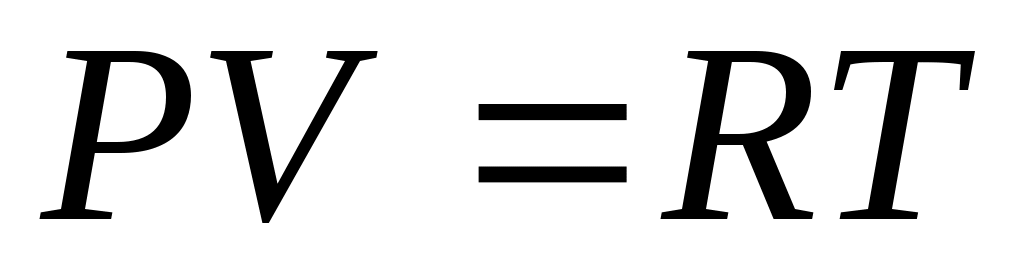 выводится в курсах физики с использованием молекулярно-кинетической теории газов. Основным допущением этой теории является предположение о том, что молекулы газа можно рассматривать как упругие шарики незначительного размера без сил взаимного притяжения. Силы отталкивания у этих шариков проявляются не на расстоянии, а только в момент столкновения друг с другом или со стенками сосуда и подчиняются законам классической механики Ньютона. выводится в курсах физики с использованием молекулярно-кинетической теории газов. Основным допущением этой теории является предположение о том, что молекулы газа можно рассматривать как упругие шарики незначительного размера без сил взаимного притяжения. Силы отталкивания у этих шариков проявляются не на расстоянии, а только в момент столкновения друг с другом или со стенками сосуда и подчиняются законам классической механики Ньютона.
Основным уравнением молекулярно-кинетической теории газов является уравнение
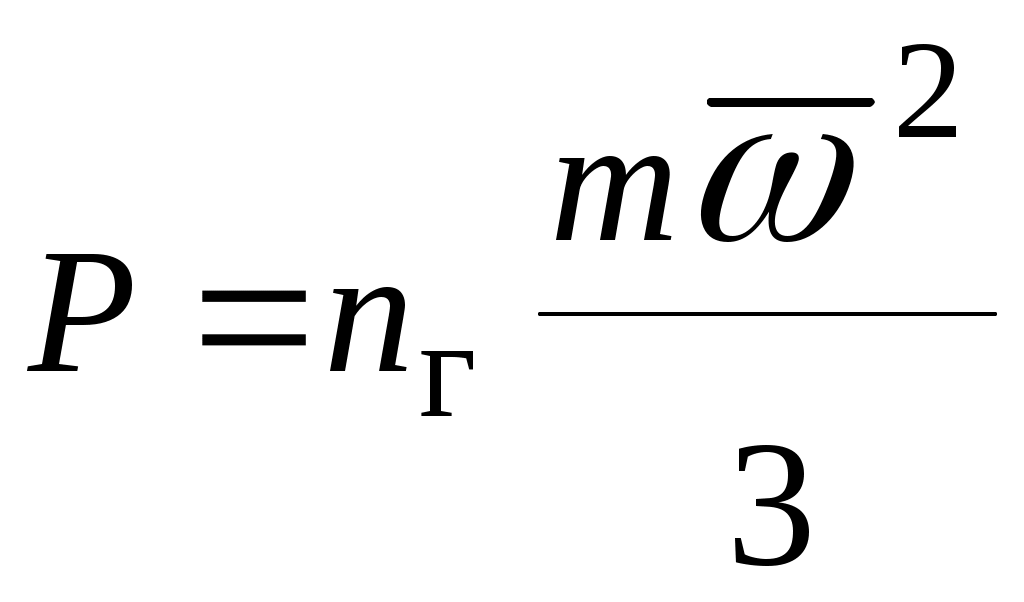 , ,
 
где: 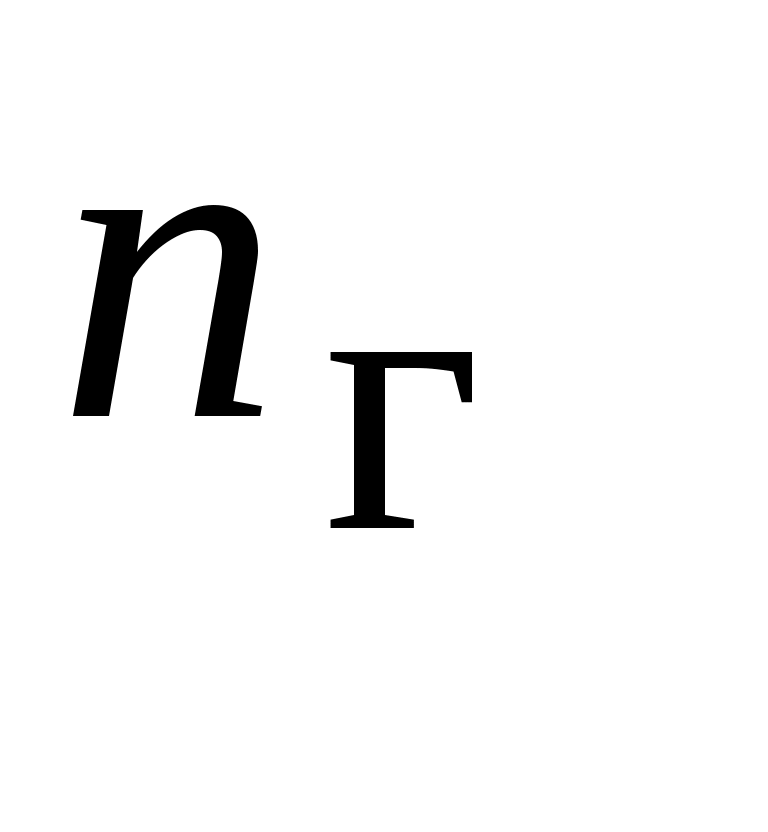 - число молекул идеального газа в 1 - число молекул идеального газа в 1 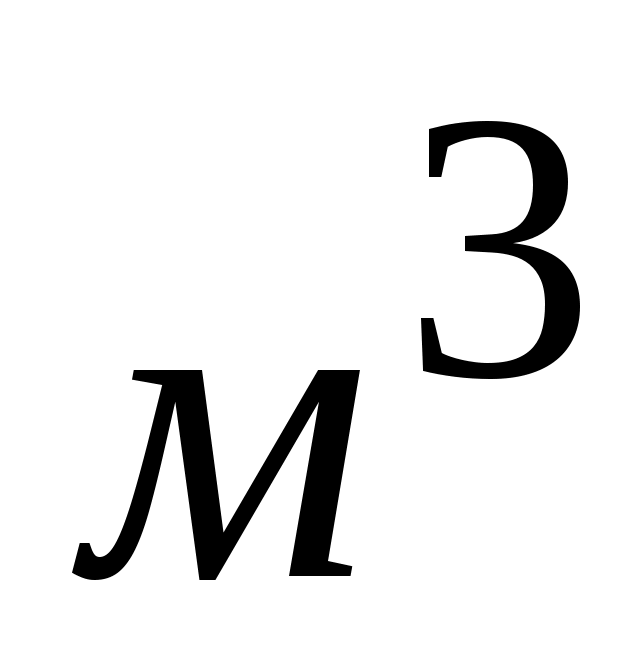 газа; газа;
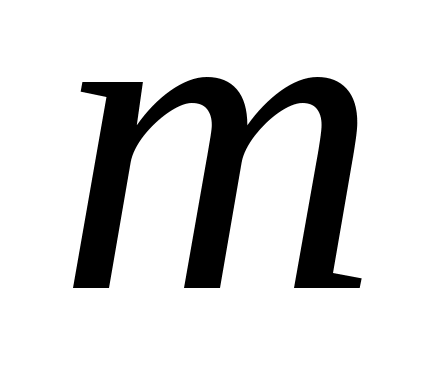 и и 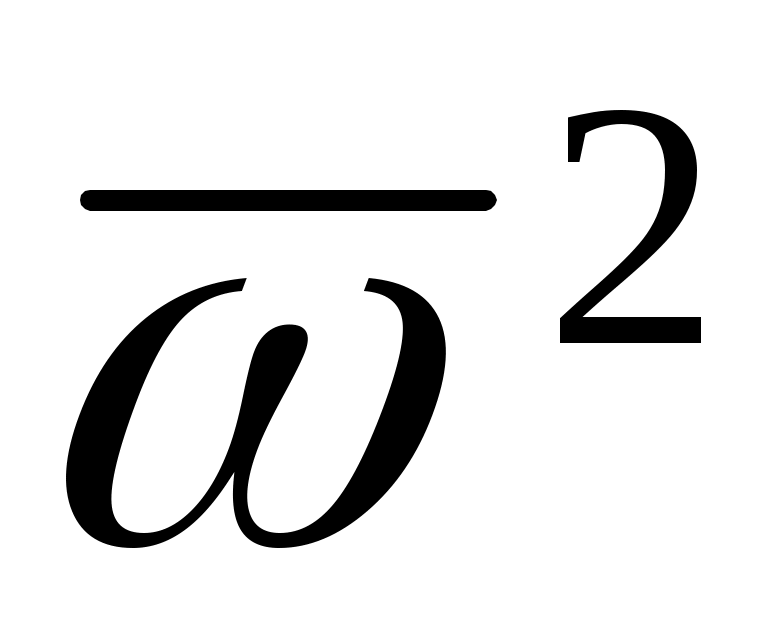 - масса молекулы и среднеквадратичная скорость ее поступательного движения. - масса молекулы и среднеквадратичная скорость ее поступательного движения.
В соответствии с выводами молекулярно-кинетической теории газов абсолютная термодинамическая температура Т определяется по формуле:
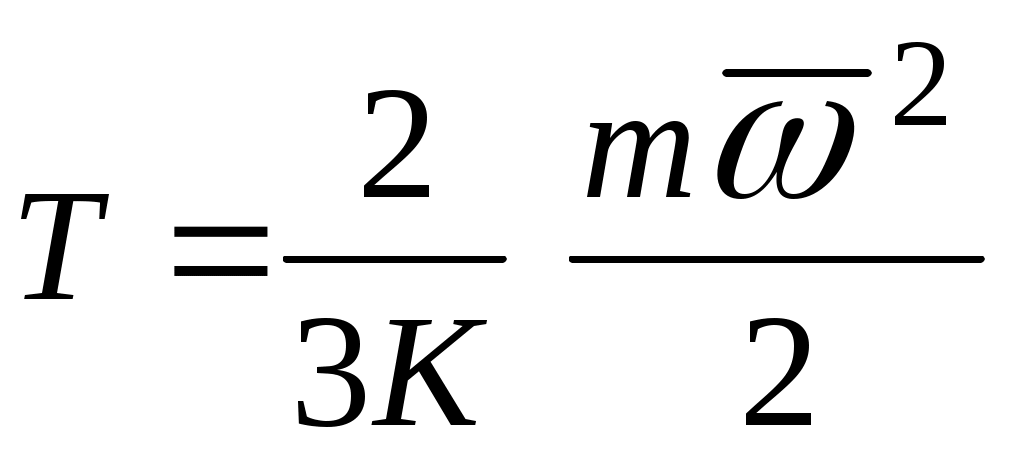 , ,
где: 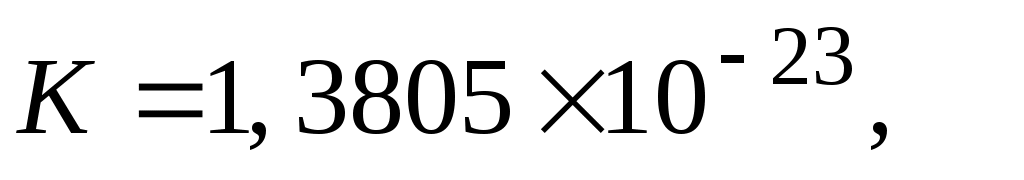 - постоянная Больцмана, Дж / К - постоянная Больцмана, Дж / К
Выразив из этого уравнение 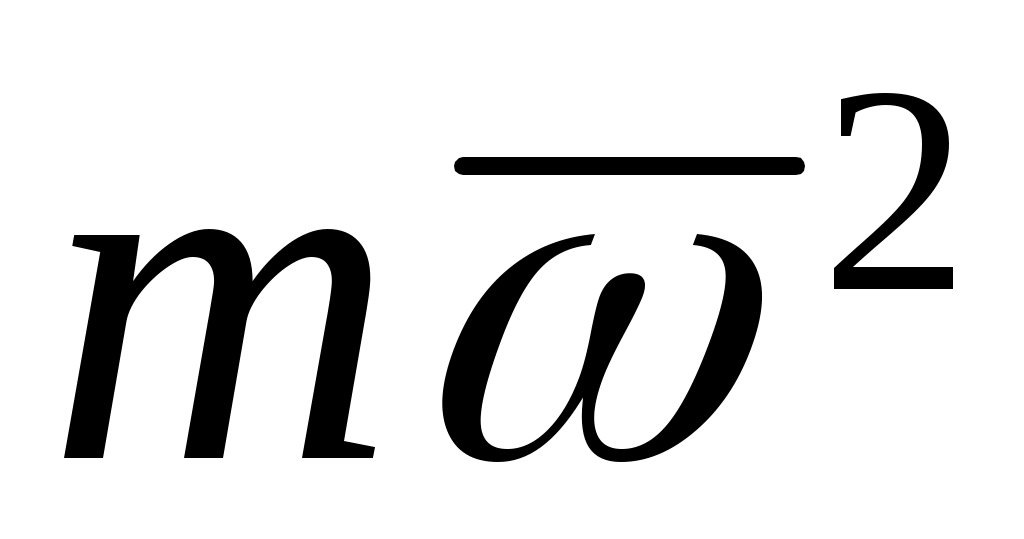 и подставив в основное уравнение молекулярно-кинетической теории газов получим: и подставив в основное уравнение молекулярно-кинетической теории газов получим:
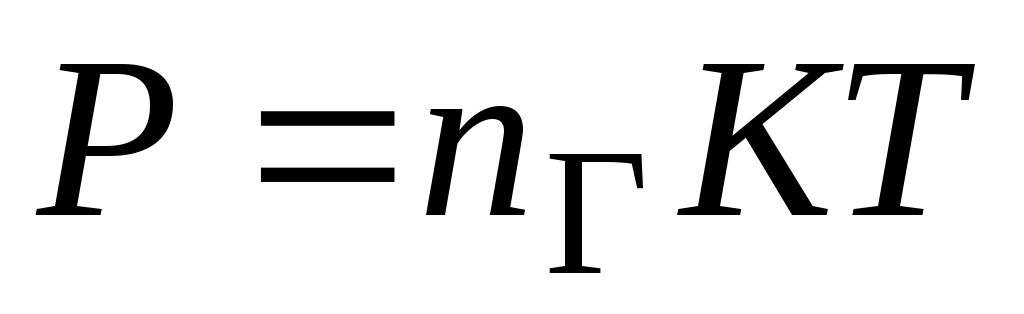
Из этого уравнения следует, что при данной температуре  давление идеального газа определяется только числом молекул в единице объема и не зависит от рода молекул. давление идеального газа определяется только числом молекул в единице объема и не зависит от рода молекул.
Для смеси идеальных газов общее число молекул 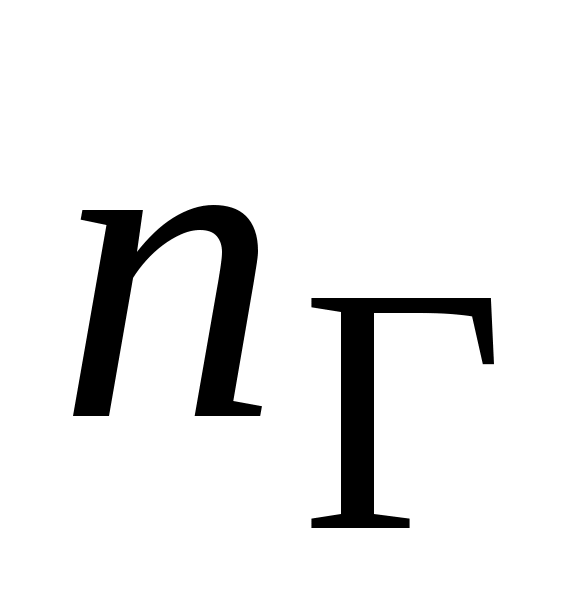 в единице объема равно сумме чисел молекул всех газов, входящих в состав смеси и равномерно распределенных в 1 в единице объема равно сумме чисел молекул всех газов, входящих в состав смеси и равномерно распределенных в 1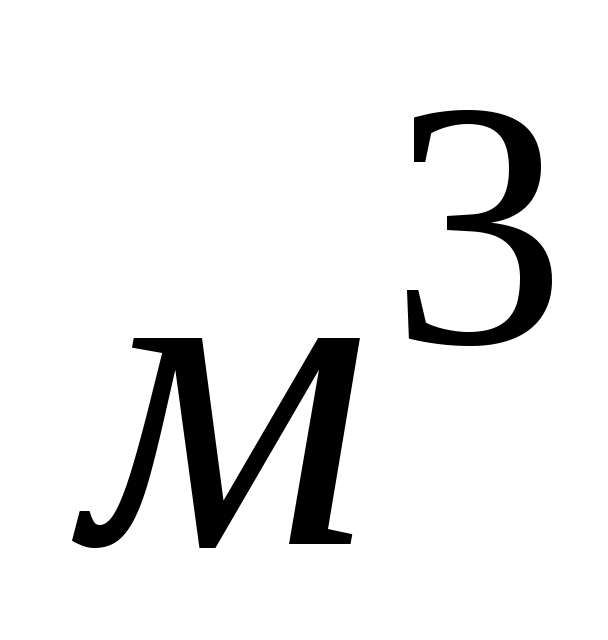 : :
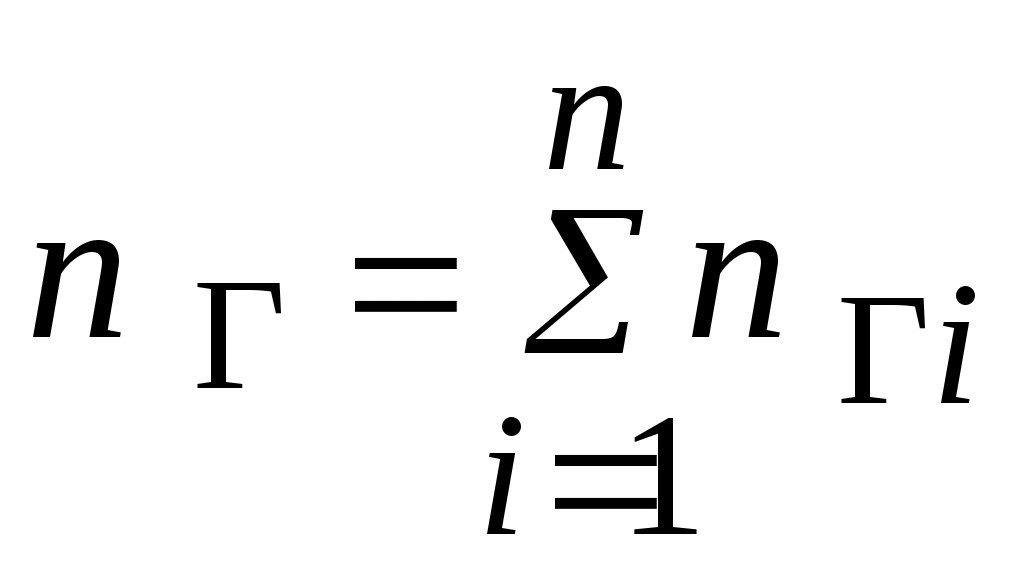
Тогда

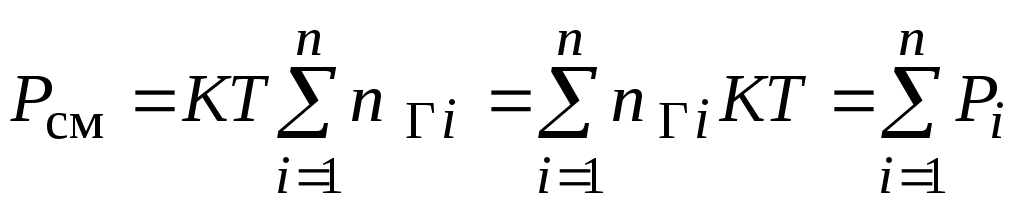
Здесь 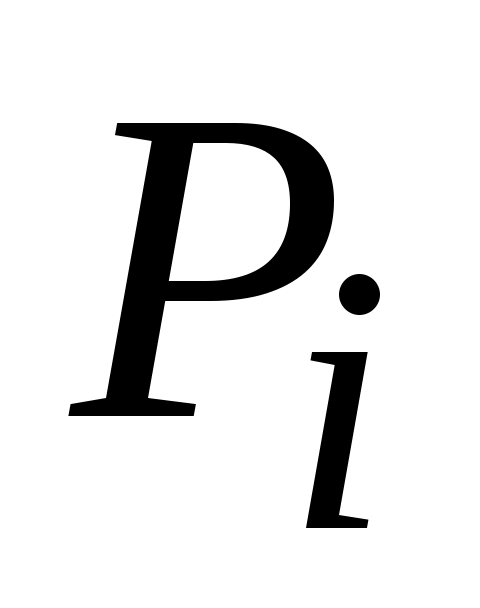 - давление, которое создавал бы i-тый газ, если бы только его молекулы в количестве - давление, которое создавал бы i-тый газ, если бы только его молекулы в количестве 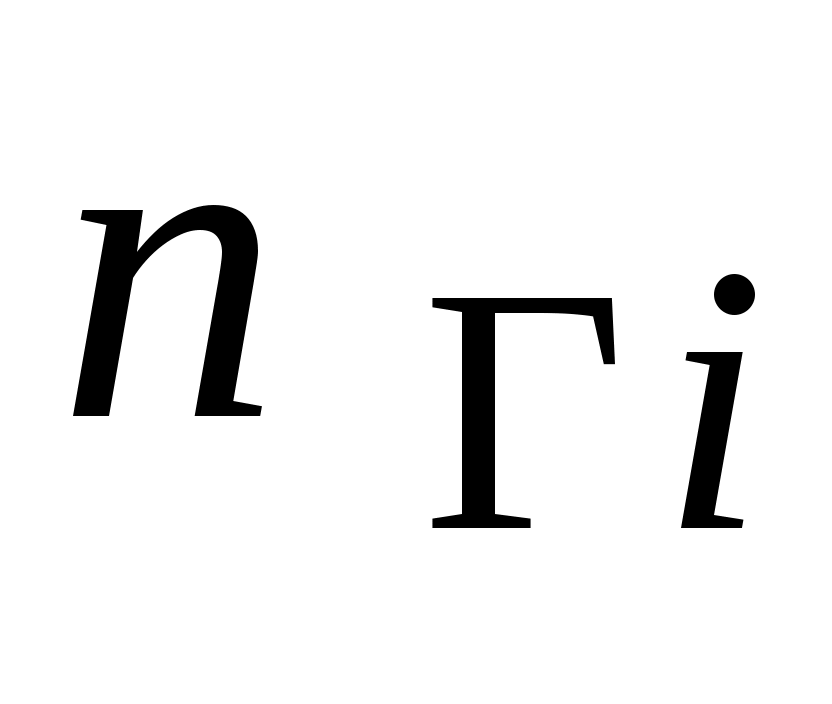 находились в 1 находились в 1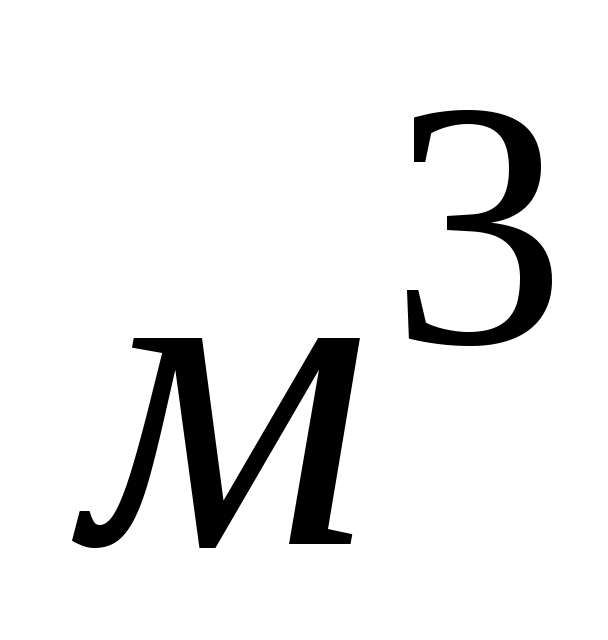 объема при температуре объема при температуре 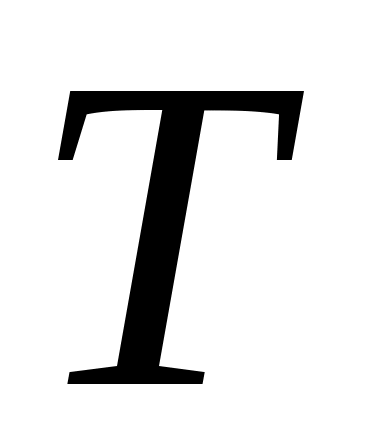 . .
Переходя в основном уравнении молекулярно-кинетической теории газов для смеси от 1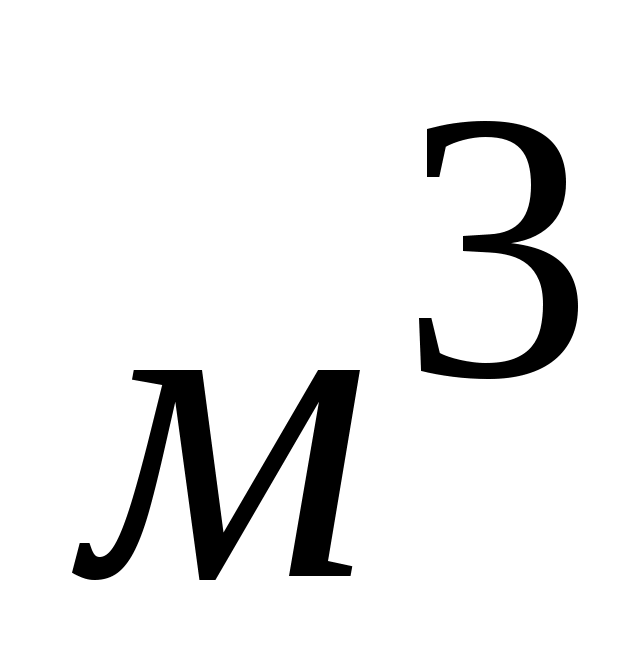 к объему смеси к объему смеси  получим получим
  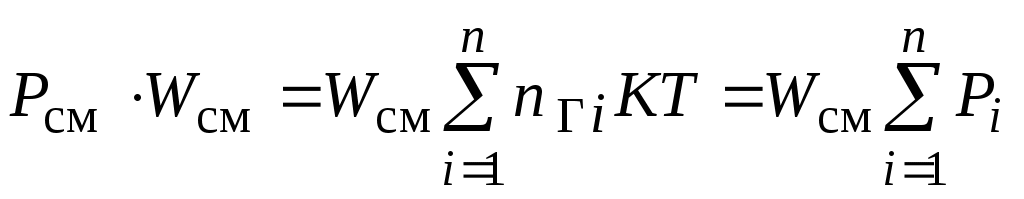
Т.е. результаты, полученные для 1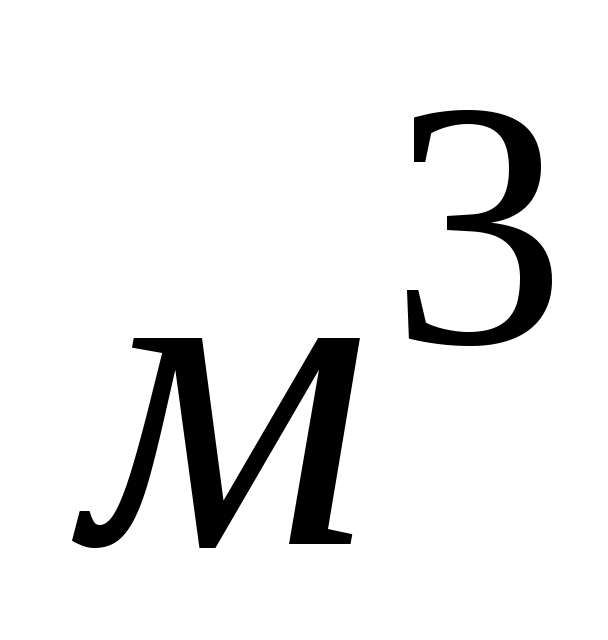 справедливы и для справедливы и для 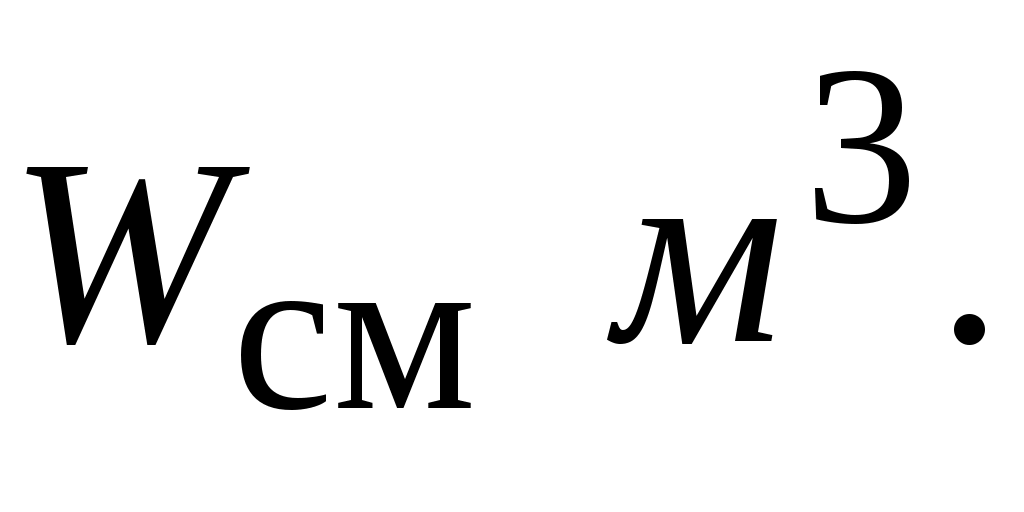
Таким образом, 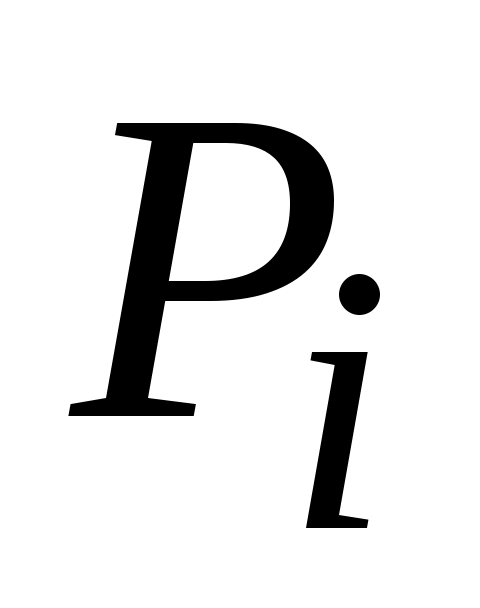 соответствует определению парциального давления и соответствует определению парциального давления и
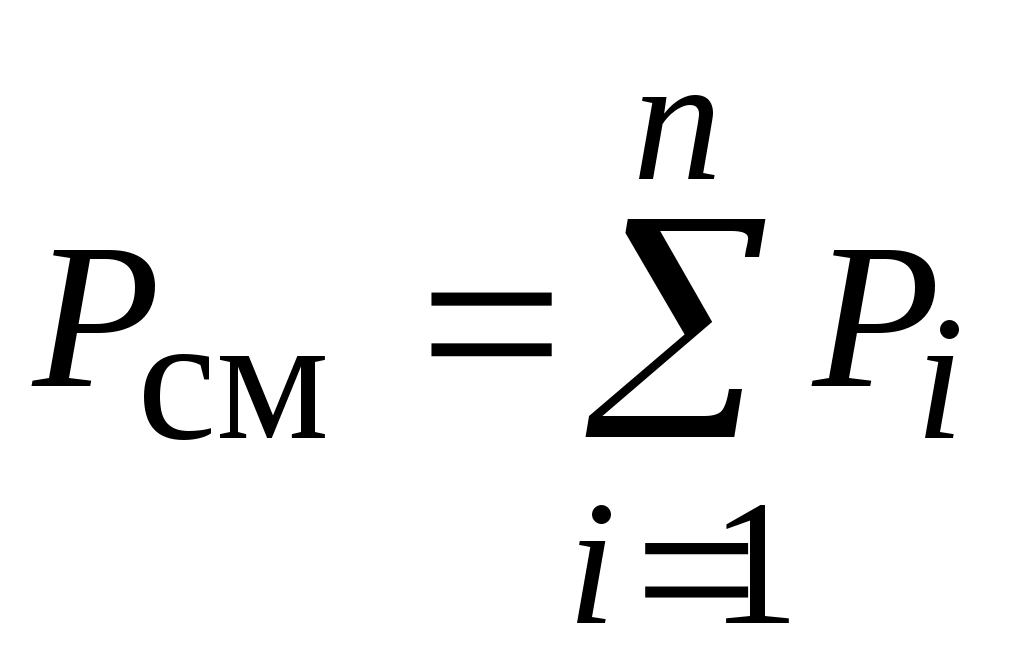 
Закон Дальтона: Общее давление смеси идеальных газов равно сумме парциальных давлений газов, составляющих смесь:
Уравнение состояния i-го газа при использовании понятия « парциальное давление » запишется следующим образом:
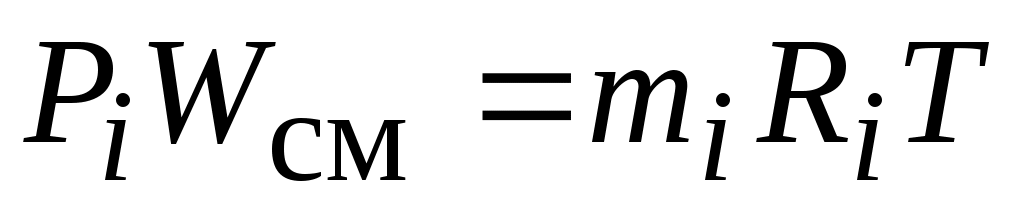
или 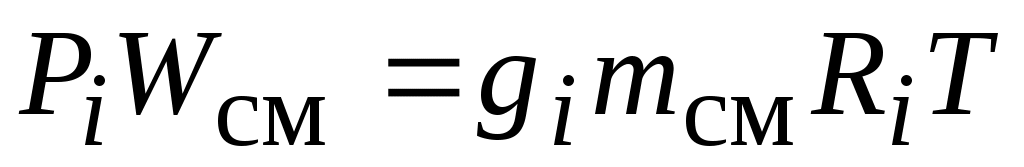
Типичной студенческой ошибкой является подстановка в это уравнение вместо объема смеси  , парциального объема , парциального объема 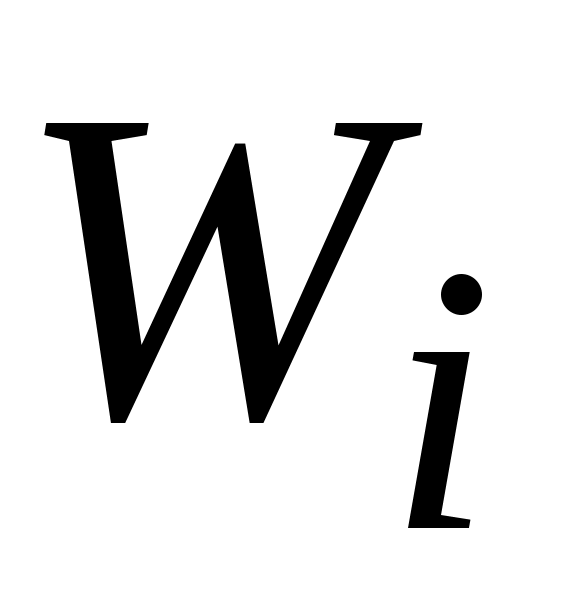 . .
1.4.3.Парциальный объем.
Для сравнения количества газов в смеси по объему, необходимо их объемы при температуре смеси привести к одинаковому давлению.
Если этим одинаковым давлением является давление смеси 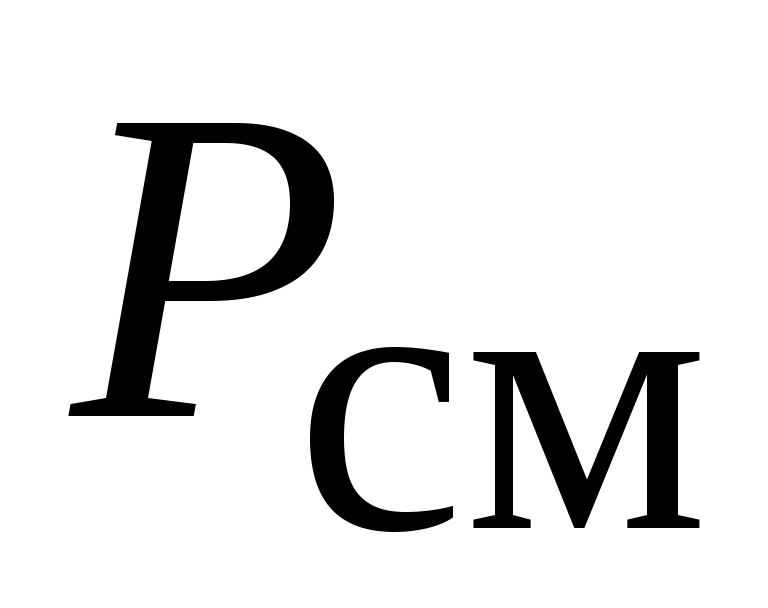 , то приведенные к этому давлению объемы компонентов называются парциальными. , то приведенные к этому давлению объемы компонентов называются парциальными.
Парциальный (приведенный) объем 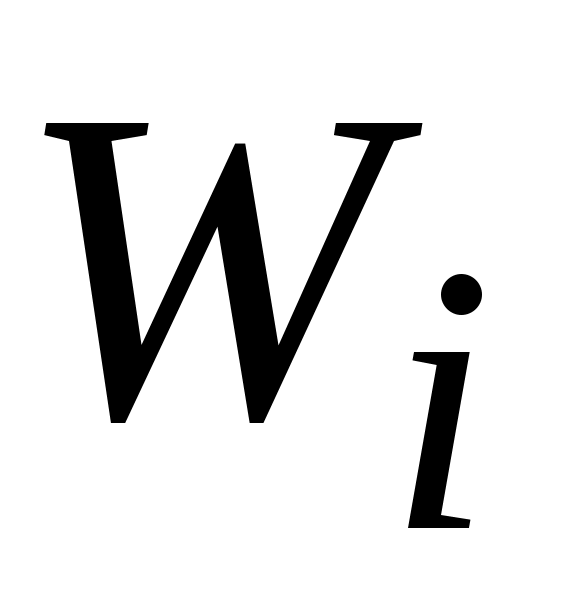 - это объем, который занимал бы i-тый компонент, если бы он один находился при температуре - это объем, который занимал бы i-тый компонент, если бы он один находился при температуре 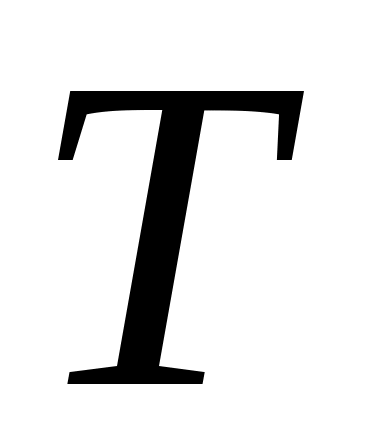 и давлении смеси и давлении смеси 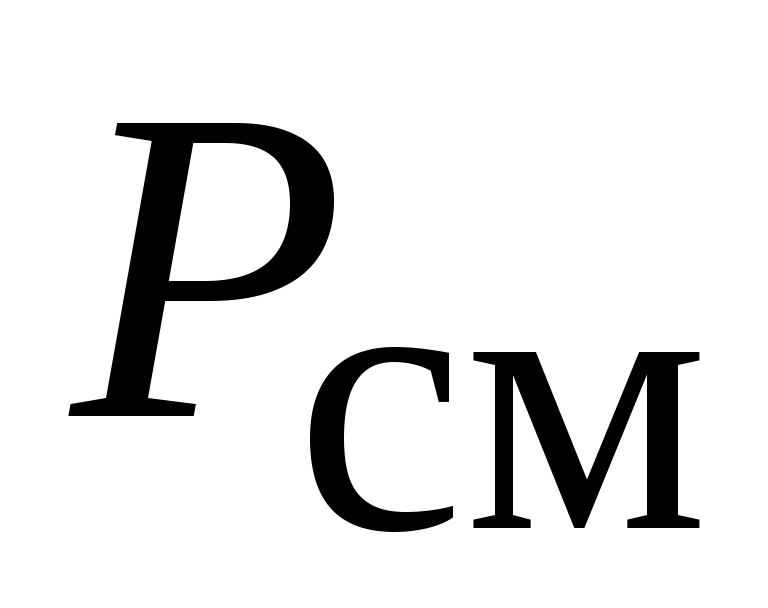 . .
Для понимания физического смысла парциального объема рассмотрим смесь двух идеальных газов. Как отмечалось ранее, молекулы обоих газов равномерно распределены по всему объему  , занимаемому смесью при давлении , занимаемому смесью при давлении 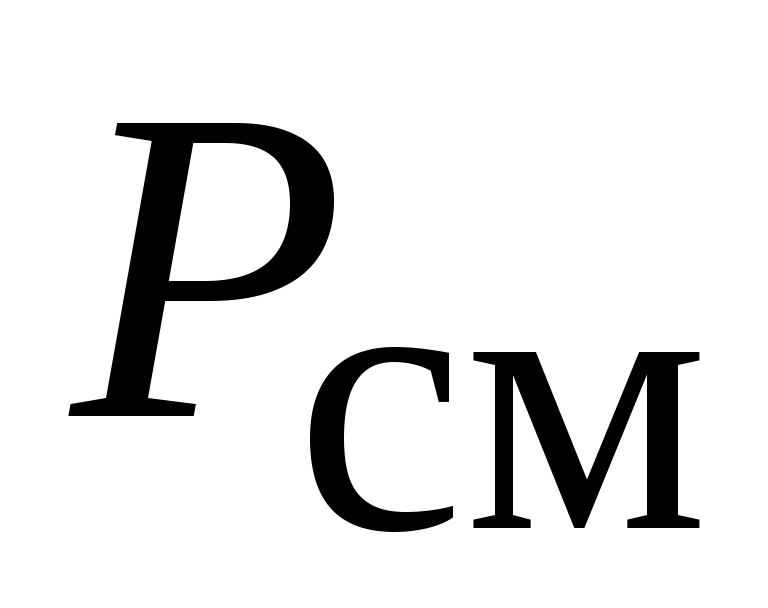 и температуре и температуре 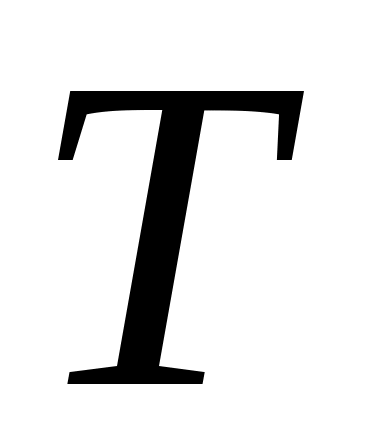 . .
Представим себе, что каким-то образом удалось разделить молекулы этих двух газов так, что в общем объеме  первый газ занимает объем первый газ занимает объем 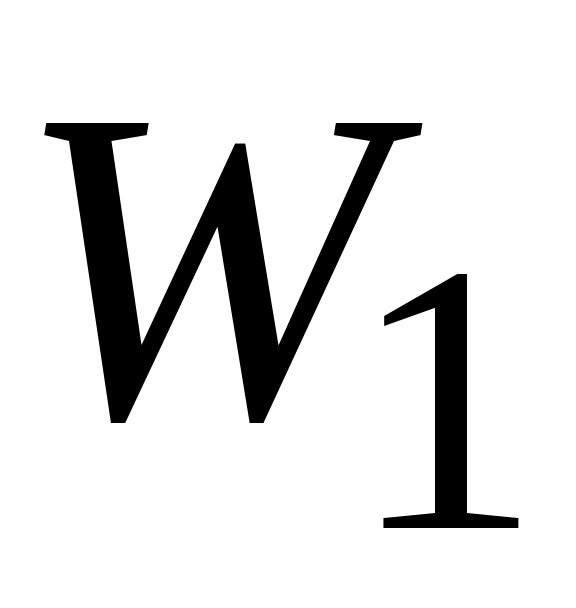 , а второй - , а второй - 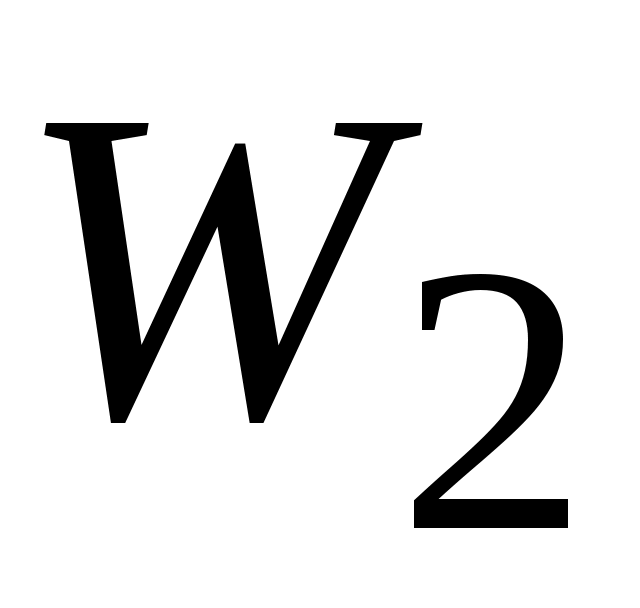 при одинаковой температуре при одинаковой температуре 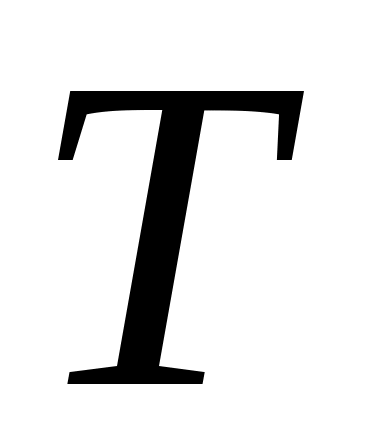 . Для того, чтобы эта гипотетическая система находилась в равновесии и газы не смешивались за счет разности давлений, давление в объемах . Для того, чтобы эта гипотетическая система находилась в равновесии и газы не смешивались за счет разности давлений, давление в объемах 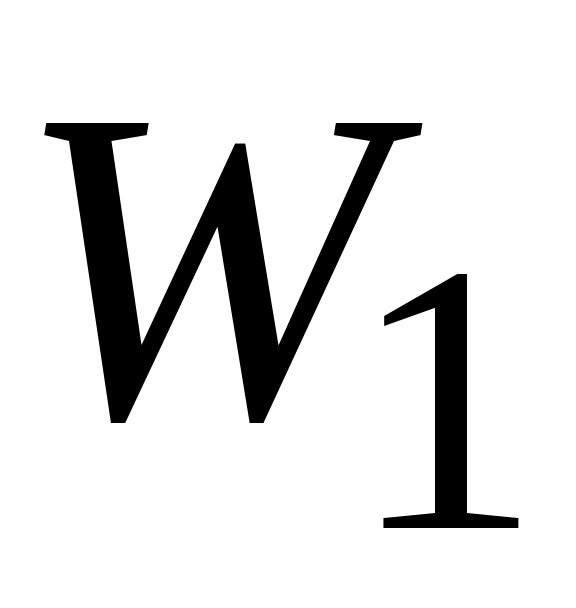 и и 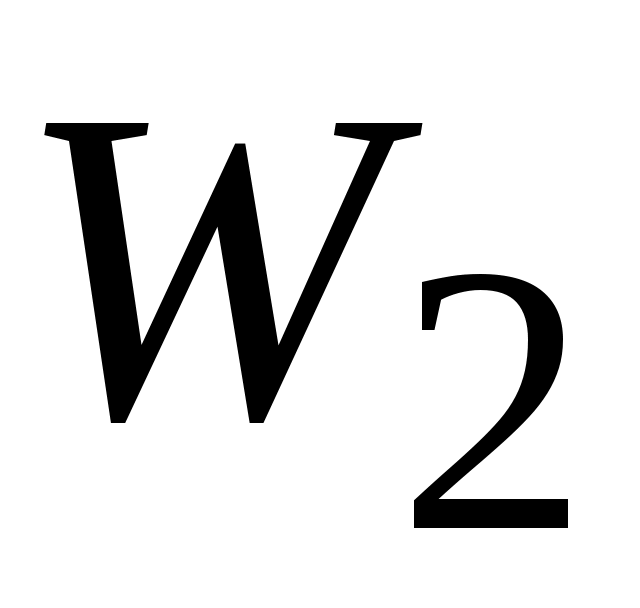 должно быть одинаковым и равным общему давлению смеси должно быть одинаковым и равным общему давлению смеси 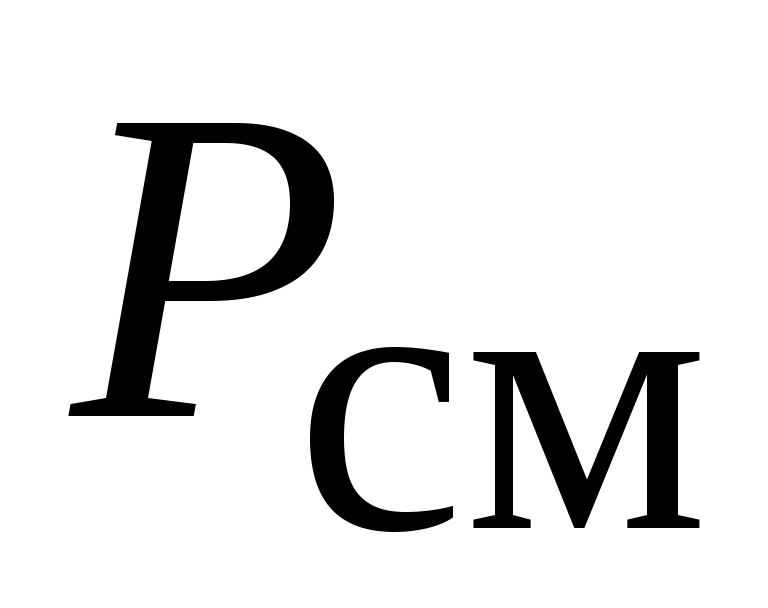 , т. е. , т. е.
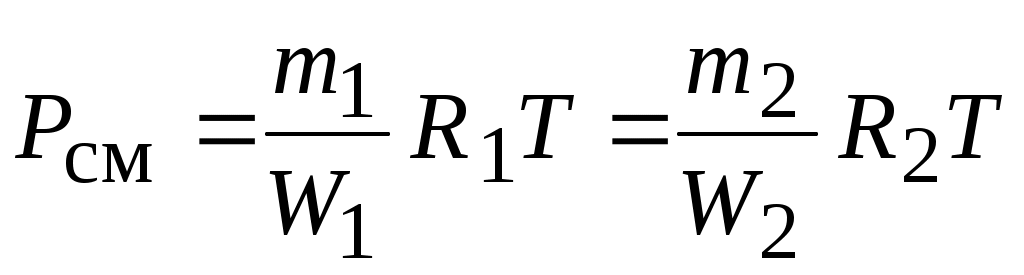
Или в общем случае 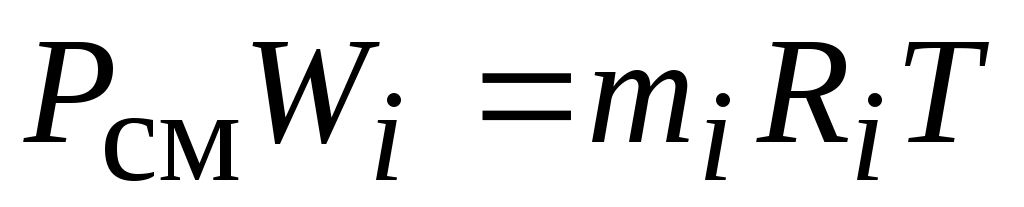
Типичной студенческой ошибкой является подстановка в это уравнение вместо давления смеси 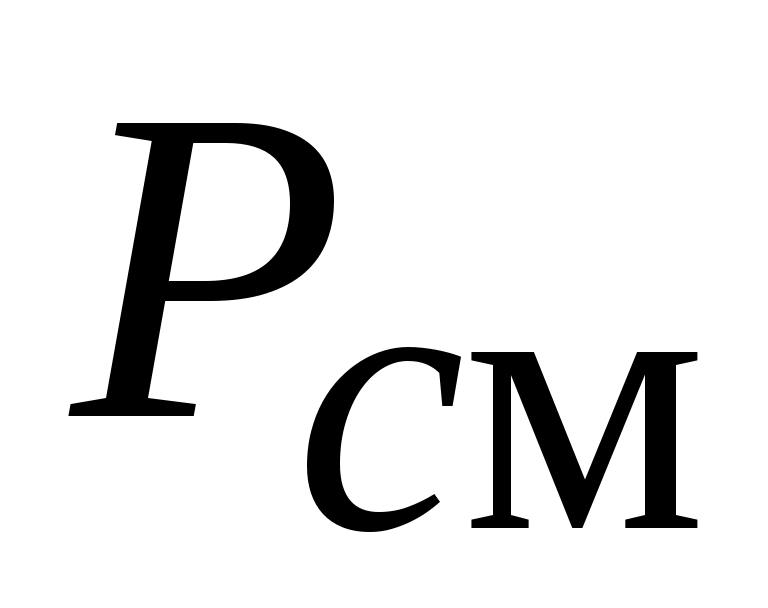 величины парциального давления величины парциального давления 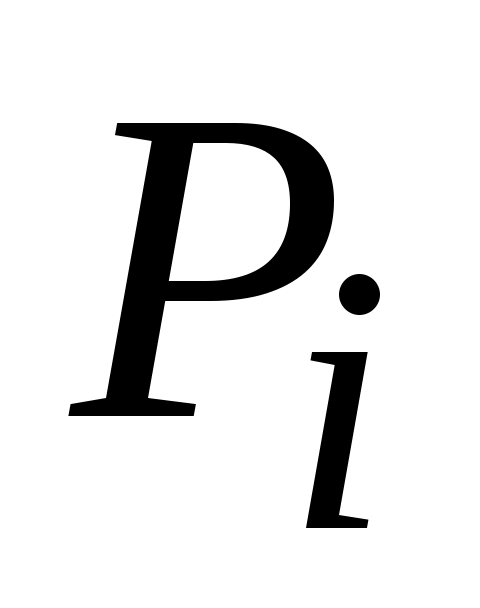 . .
1.4.4. Задание состава смеси идеальных газов объемными долями.
Во многих практических задачах состав смеси газов задается объемными долями:
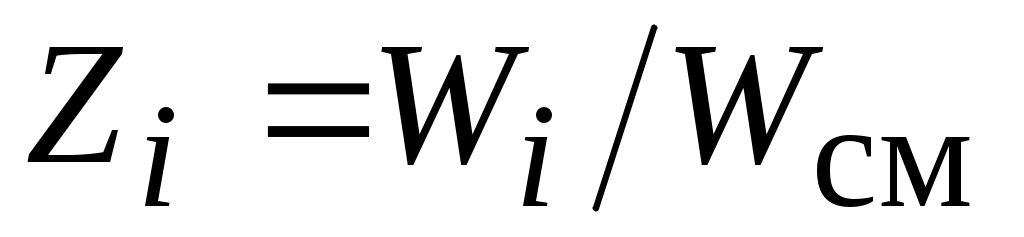 , ,

где: 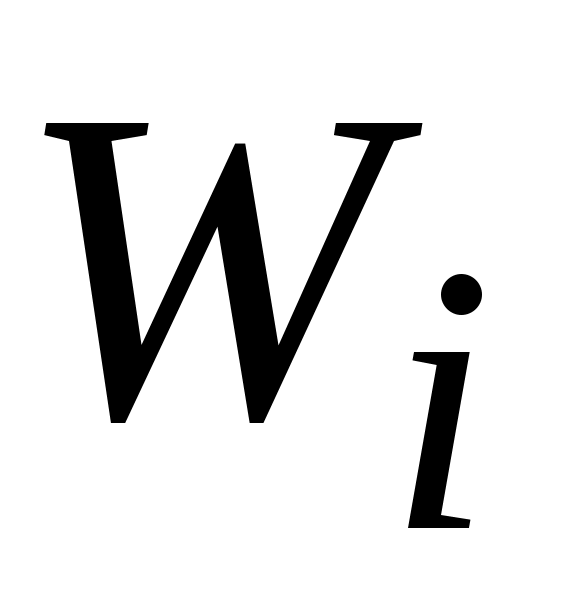 - парциальный объем i-го газа в составе смеси газов, занимающей объем - парциальный объем i-го газа в составе смеси газов, занимающей объем  . .
Установим связь между объемными и мольными долями газов смеси.
Т. к. универсальная газовая постоянная 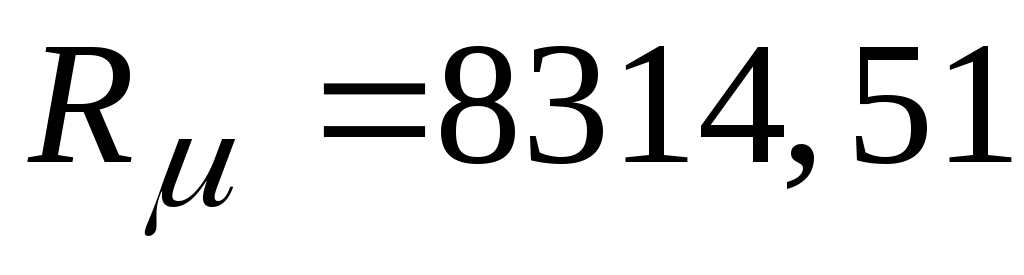 Дж / (кмоль · К) Дж / (кмоль · К)
связана с удельными газовыми постоянными 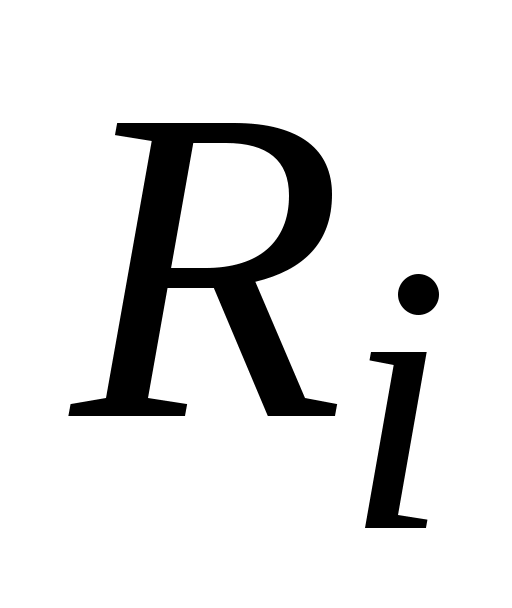 , Дж / (кг · К), соотношением , Дж / (кг · К), соотношением
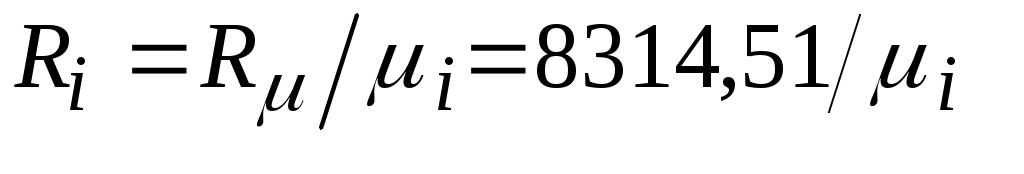 , ,
то из определения парциального объема идеального газа в составе смеси получим:
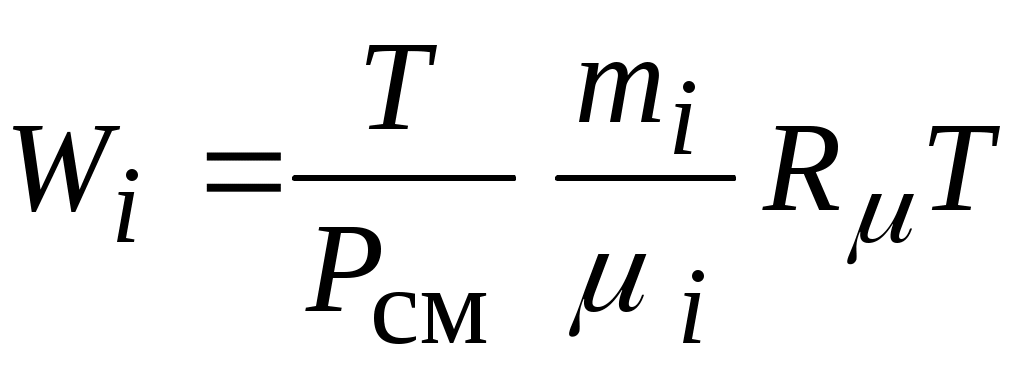 или или 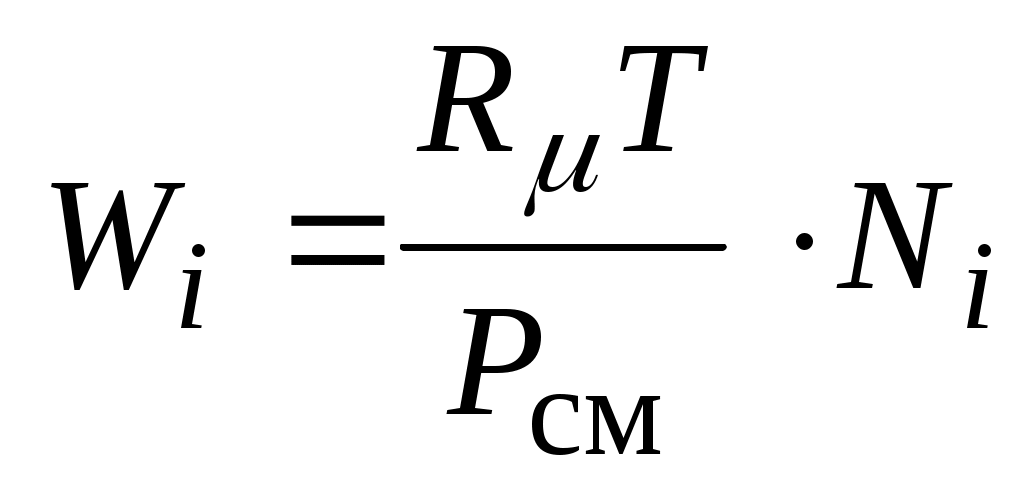 , ,
где: 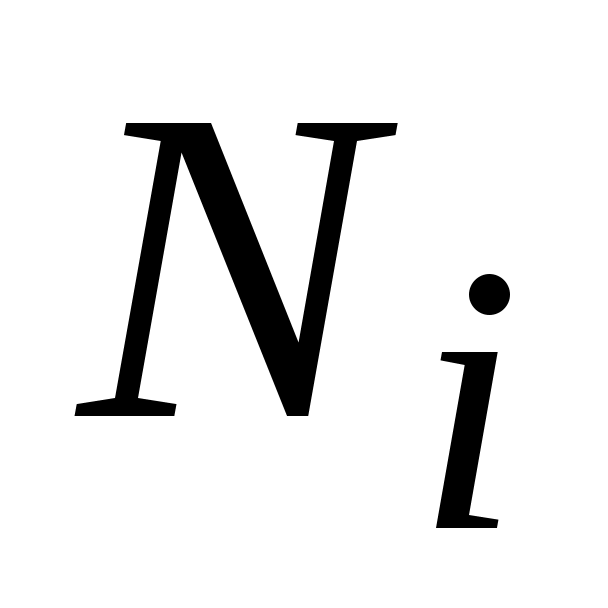 -число киломолей i-го газа. -число киломолей i-го газа.
Просуммировав значения 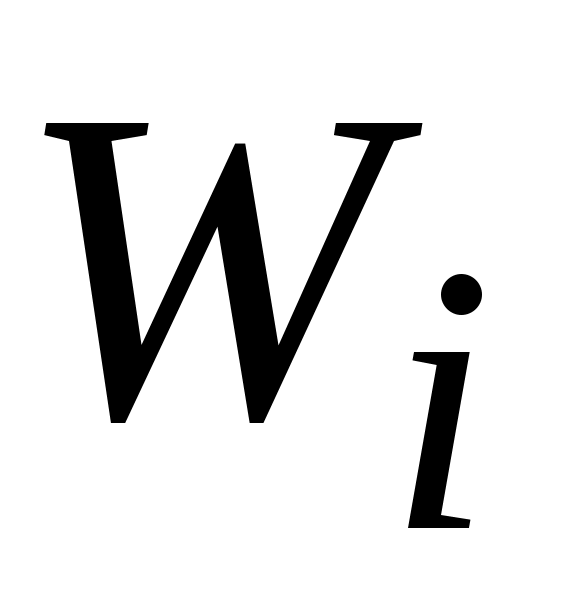 для всех газов, входящих в смесь, получим для всех газов, входящих в смесь, получим
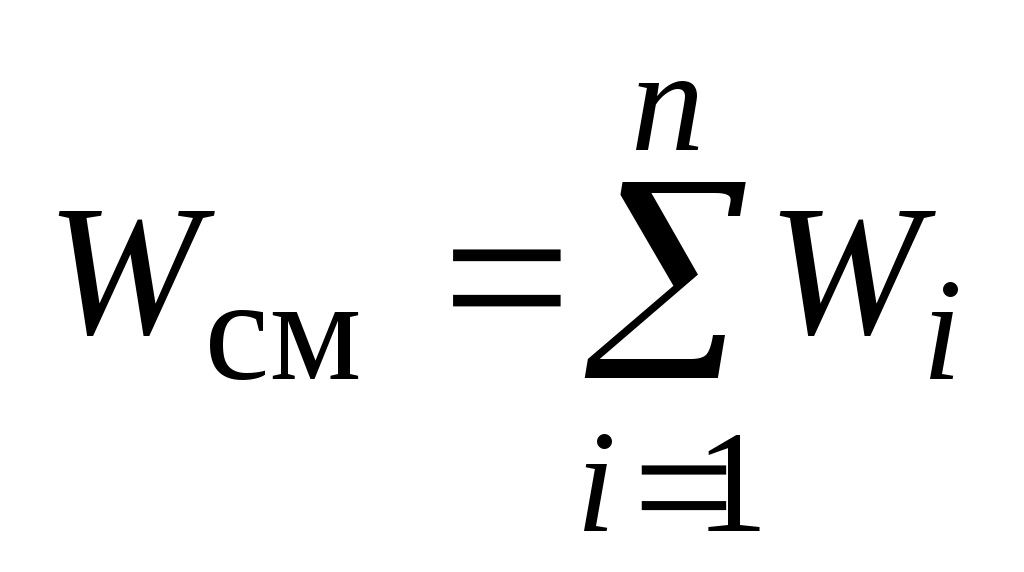 , ,
где: 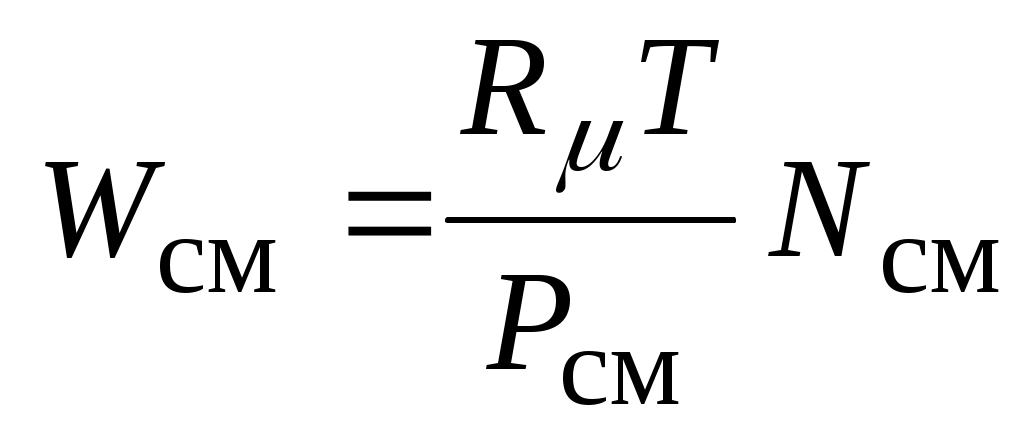 и и 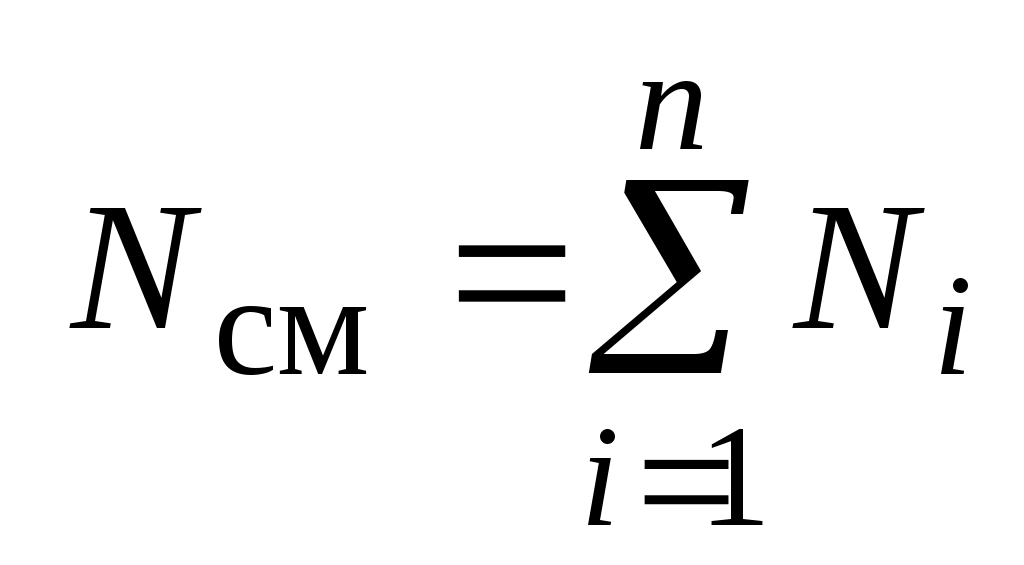
Разделив выражения для 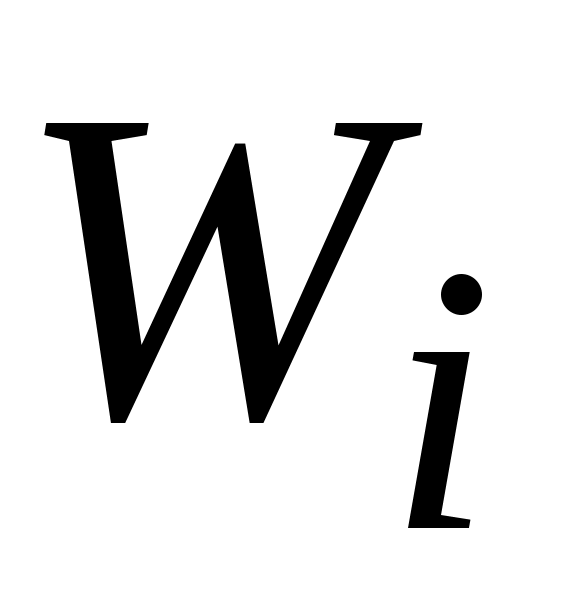 на выражение для на выражение для  получим получим
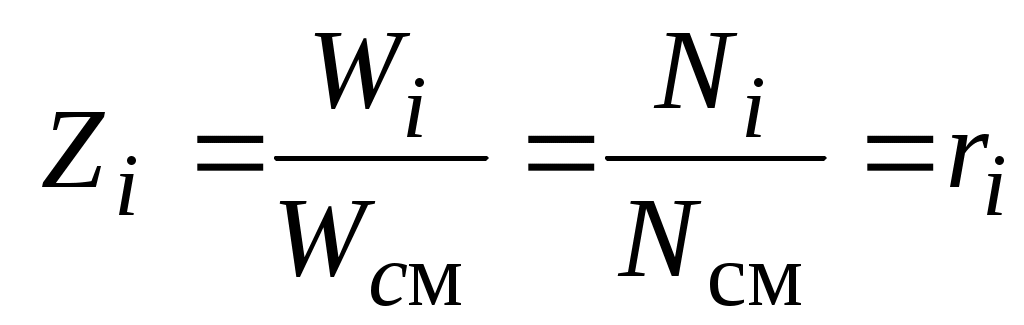
Т. о. для смеси идеальных газов мольная и объемная доли i-го газа равны между собой по величине
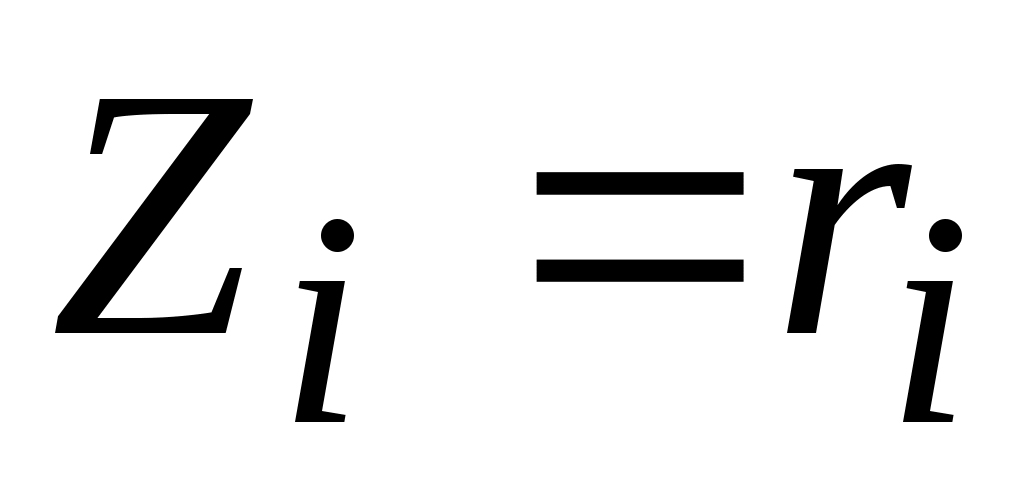 . .
и
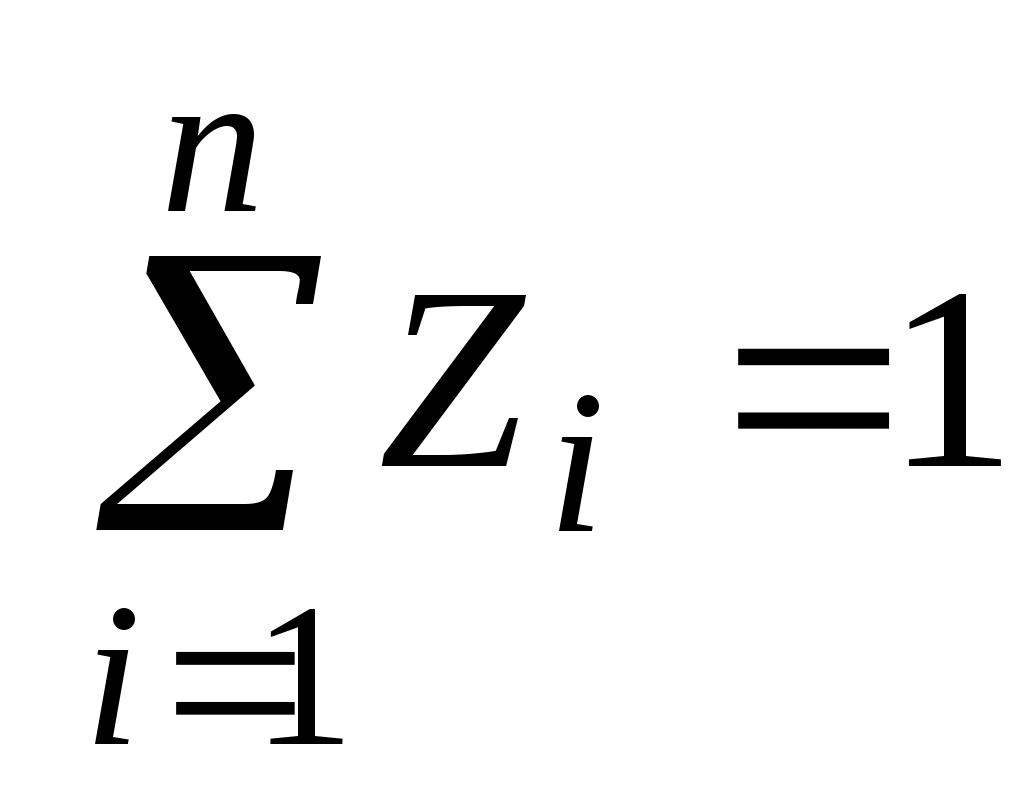 . .
1.4.5. Формулы пересчета для различных способов задания состава газовых смесей
Получим формулу пересчета мольных долей на массовые и наоборот.
Т. к. 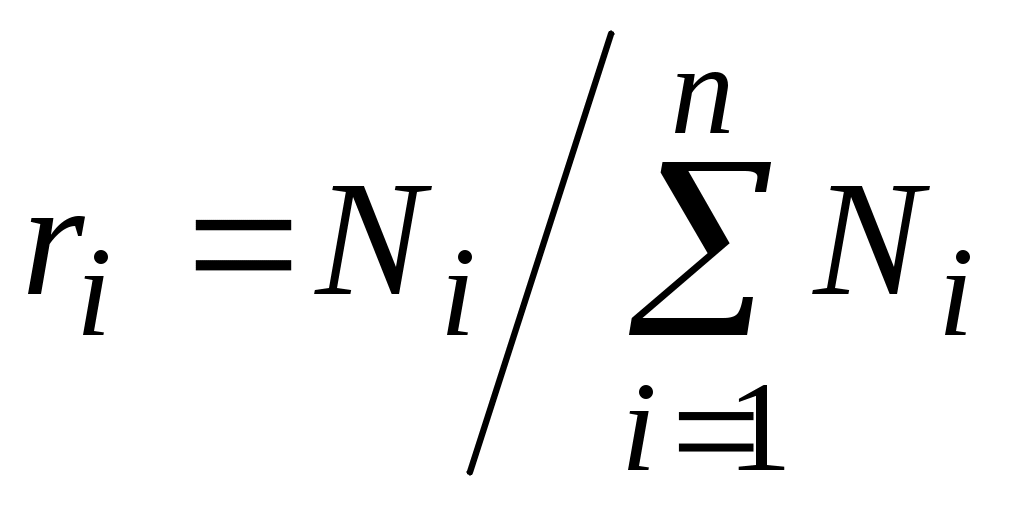 и и 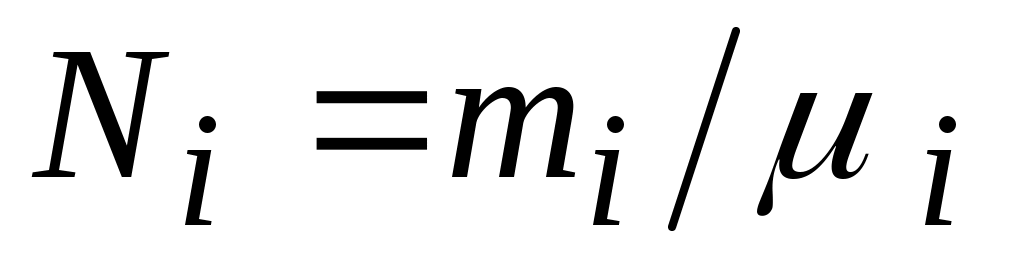 , то , то 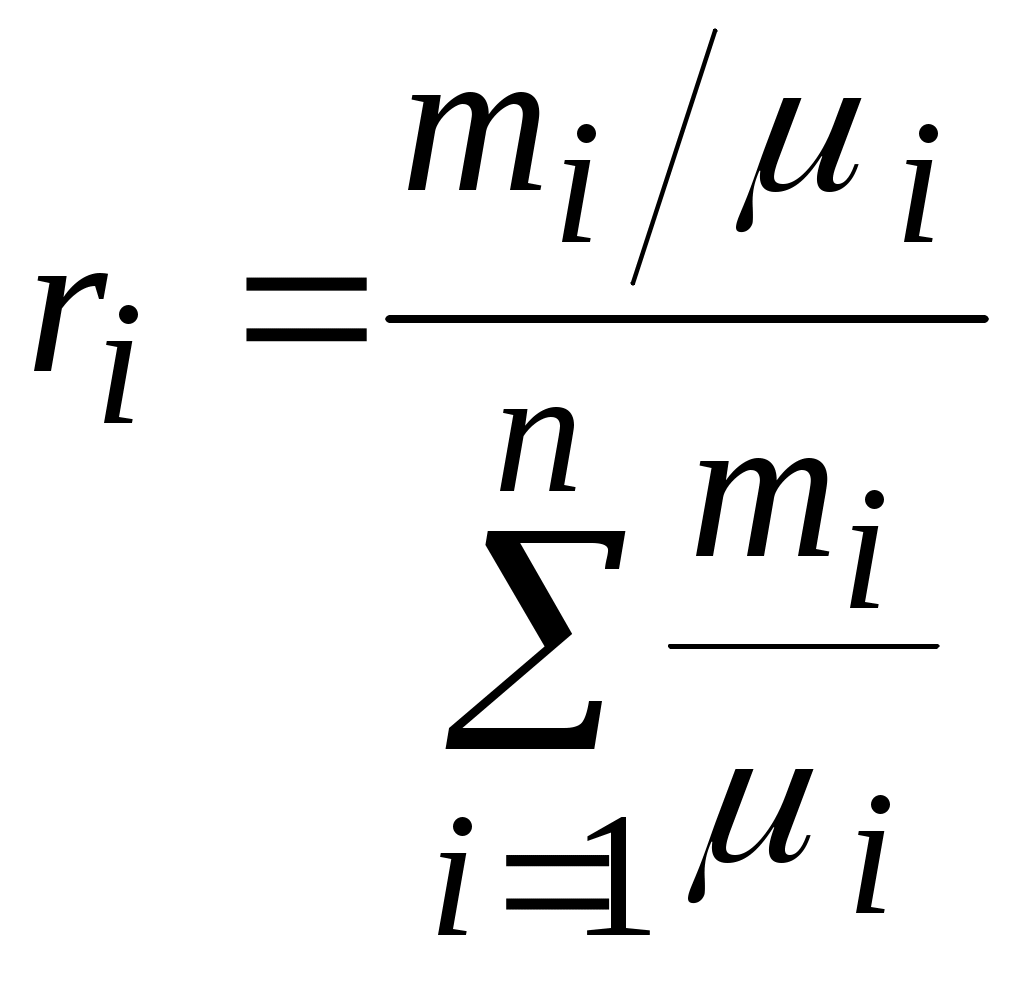 . .
Разделив числитель и знаменатель полученного выражения на массу смеси 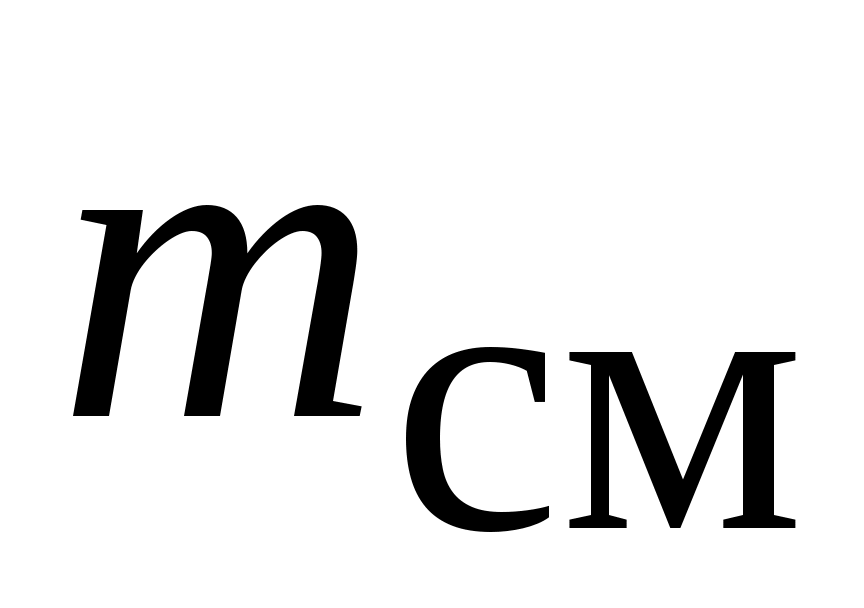 получим получим
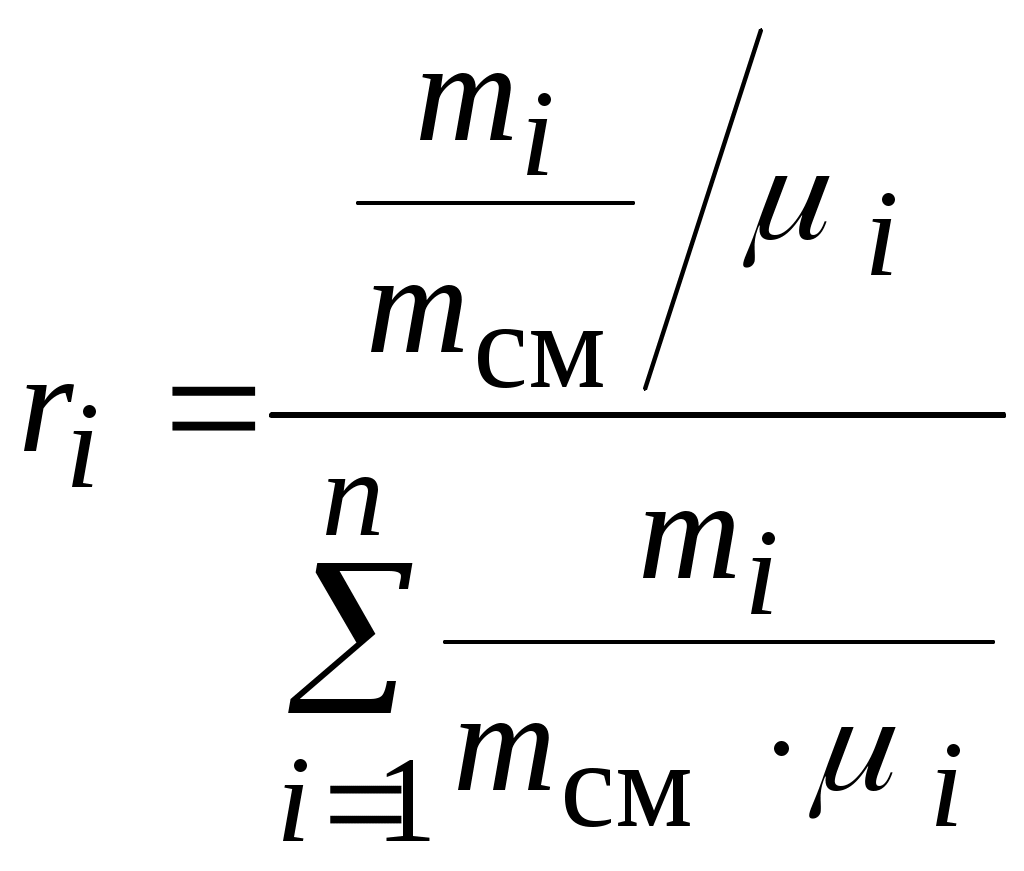 , ,
или окончательно:
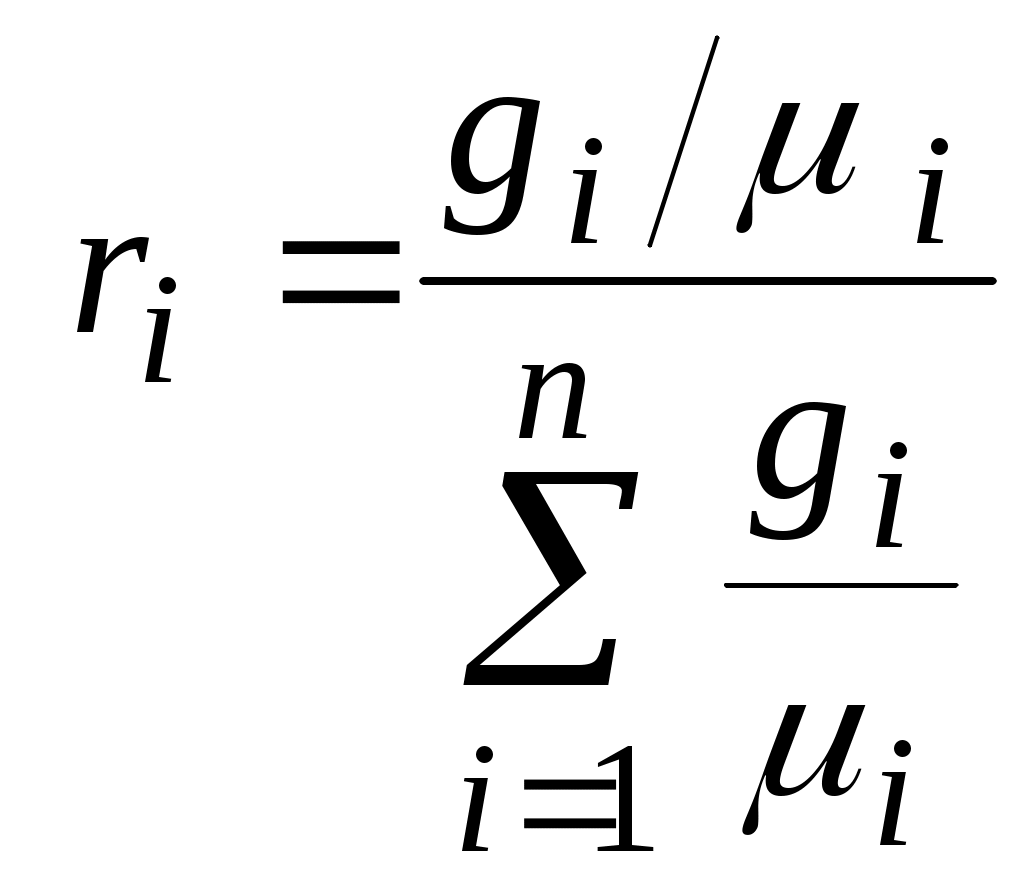
Т. к. 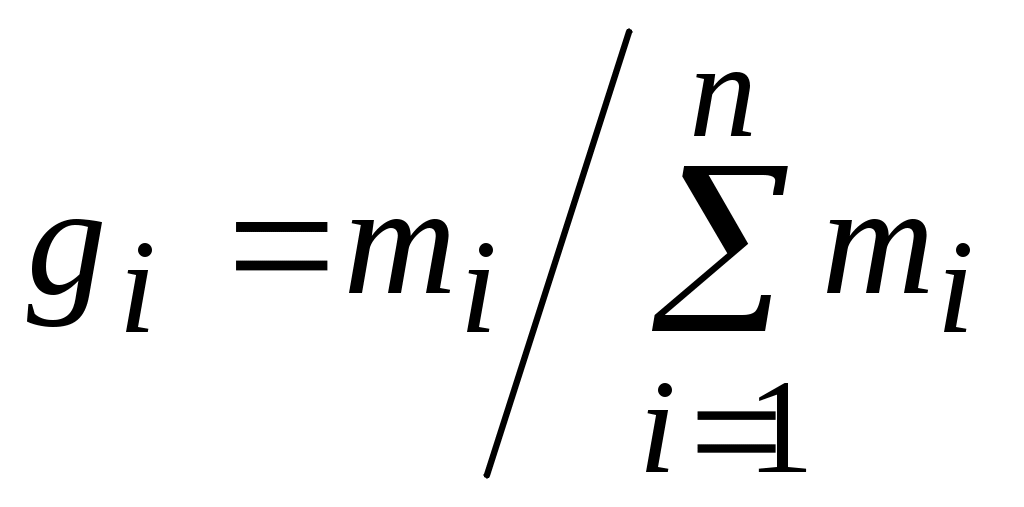 и и 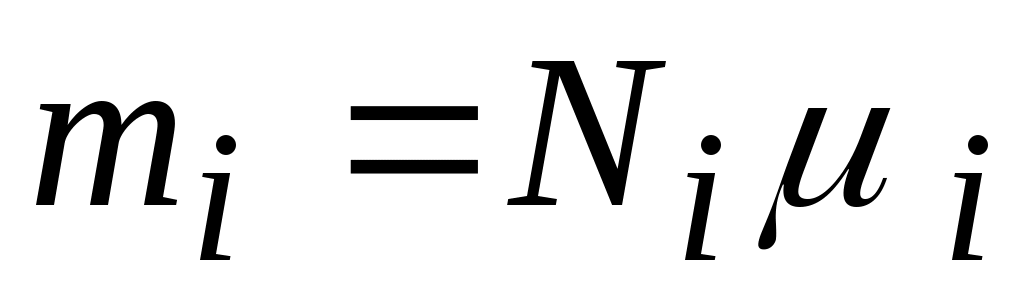 , ,
то 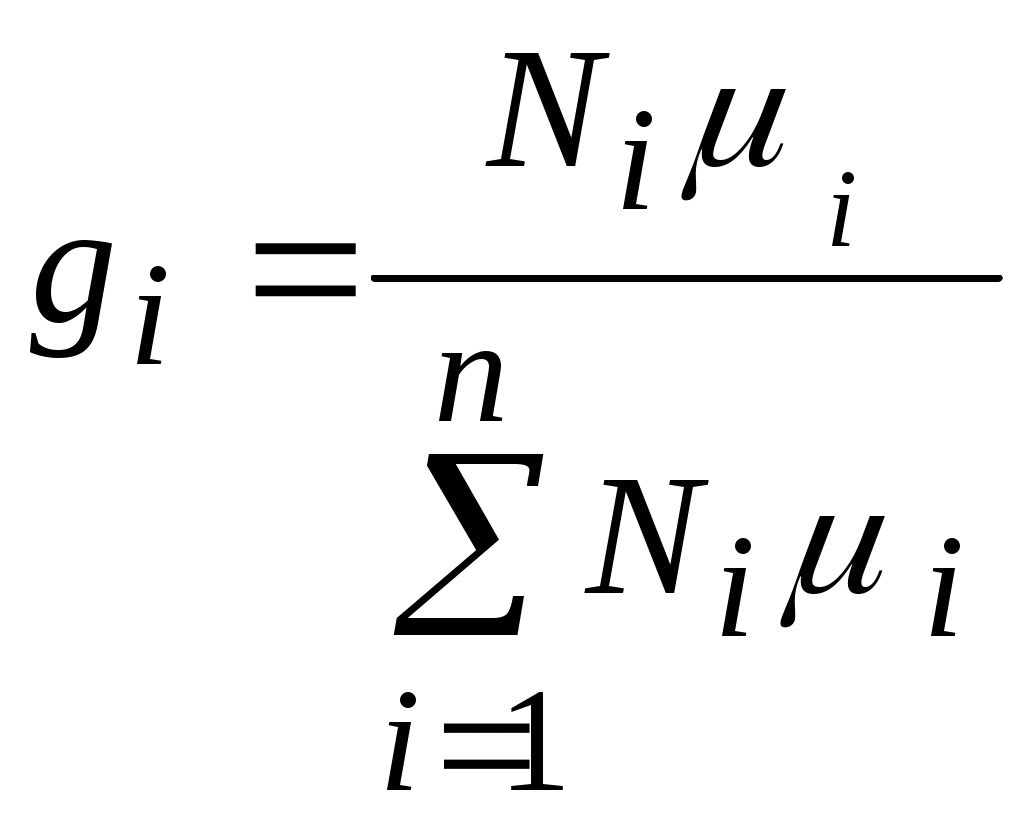 . .
Разделив числитель и знаменатель этого выражения на 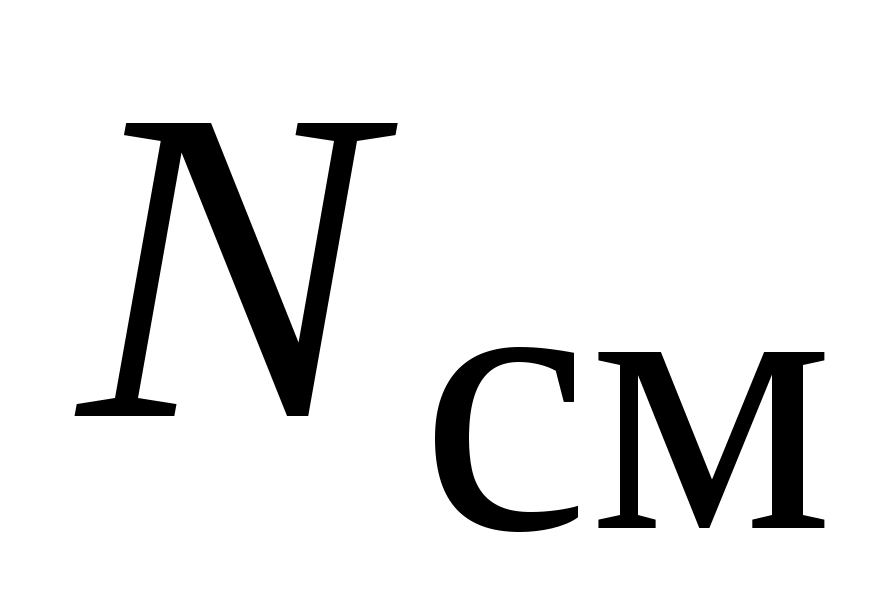 получим получим 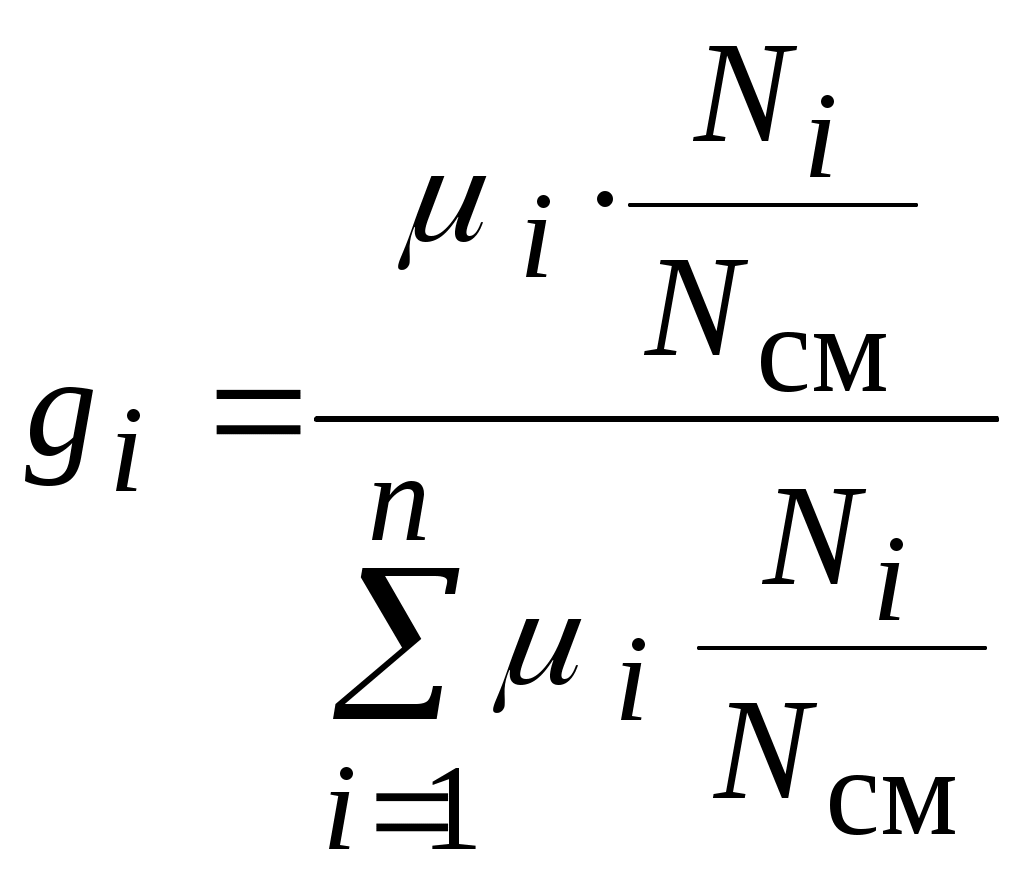 , ,
или окончательно
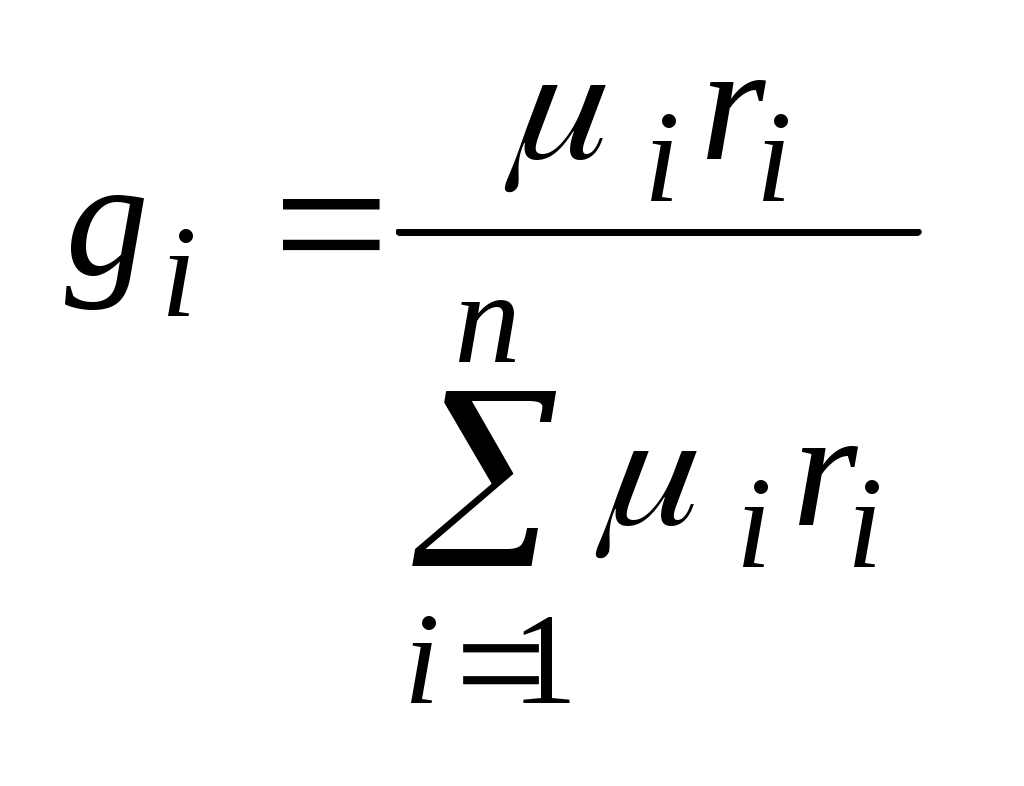
1.4.6. Кажущаяся молекулярная масса смеси газов
Для упрощения расчетов смесь идеальных газов условно полагают однородным газом с той же суммарной массой 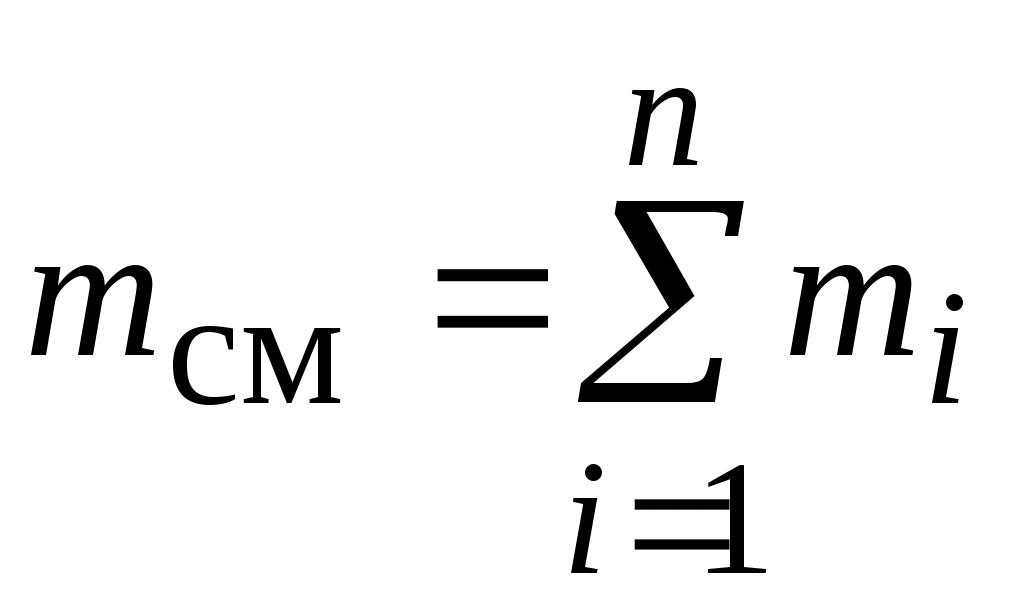 и с тем же суммарным числом молекул, равным и с тем же суммарным числом молекул, равным
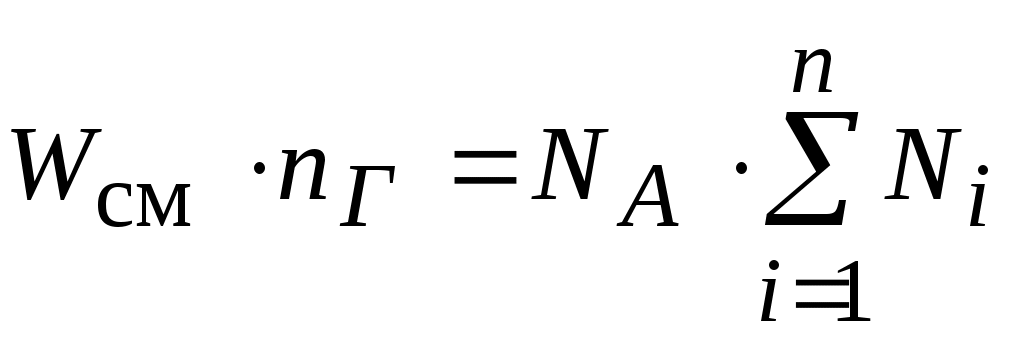 , ,
где 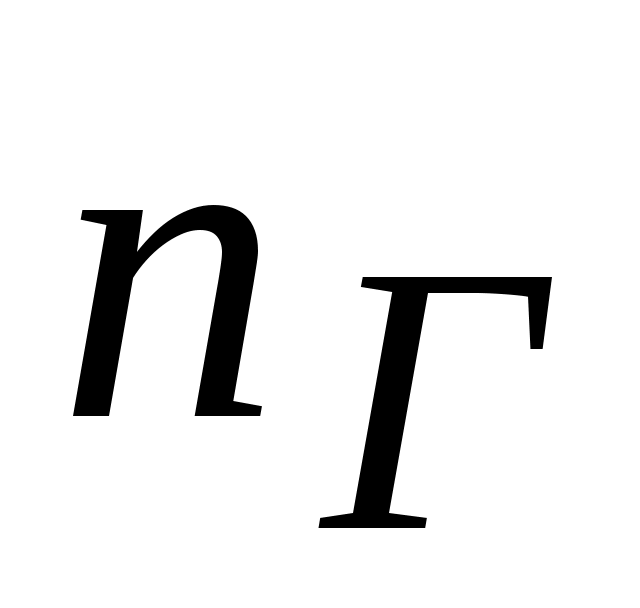 - число молекул в единице объема смеси газов; - число молекул в единице объема смеси газов;
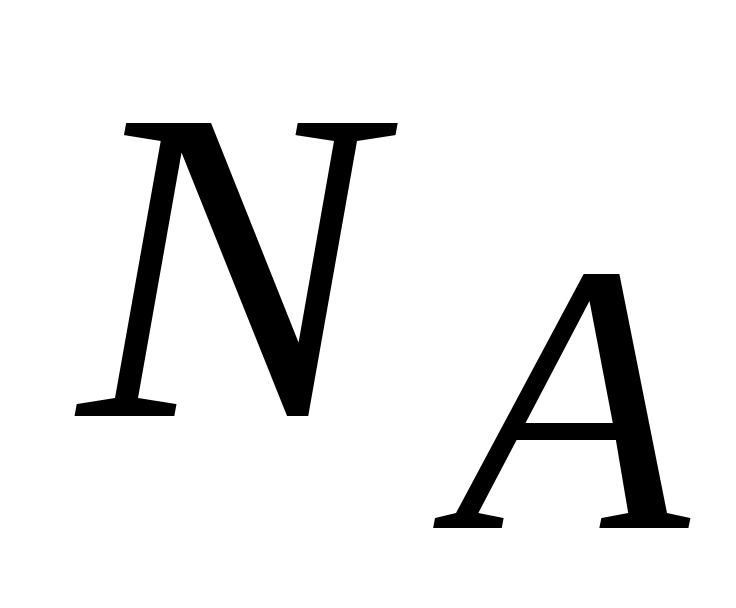 - число Авогадро (число молекул в одном киломоле вещества): - число Авогадро (число молекул в одном киломоле вещества):
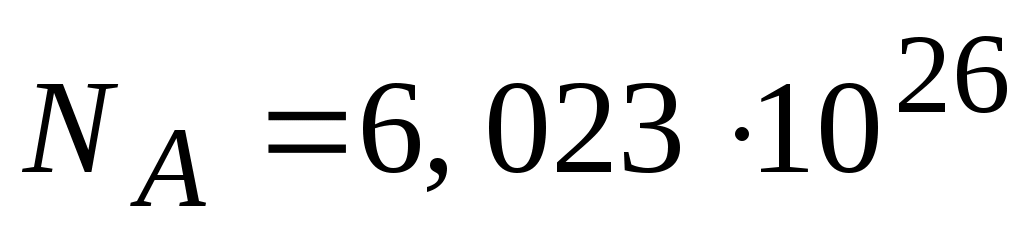 , 1 / кмоль , 1 / кмоль
Молекулярная масса такого однородного газа обозначается 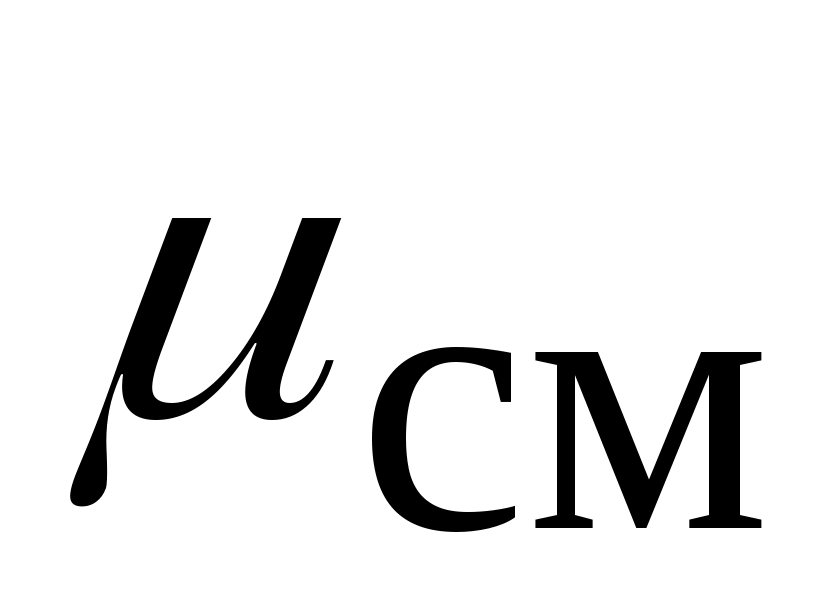 и называется кажущейся молекулярной массой смеси: и называется кажущейся молекулярной массой смеси:
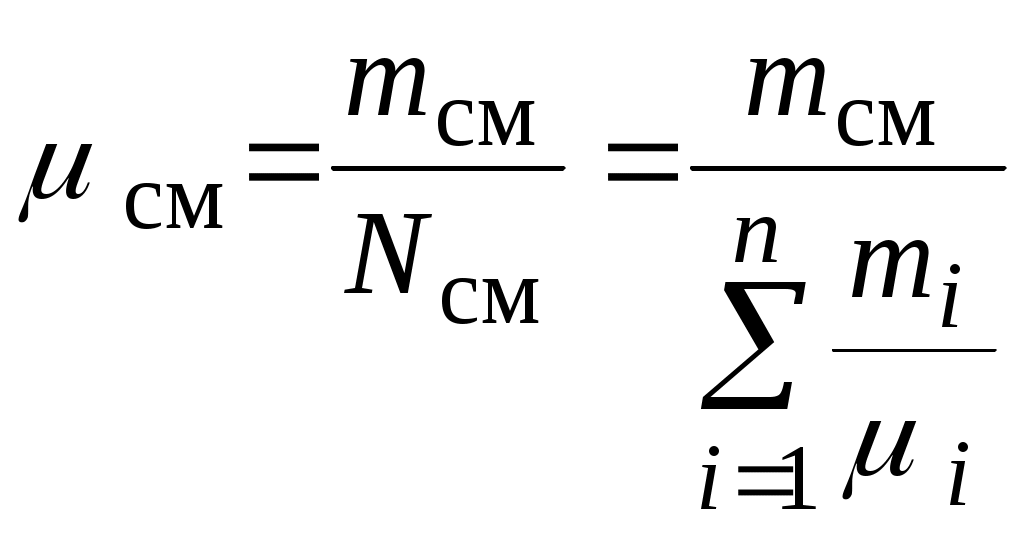 . .
Разделив числитель и знаменатель этого выражения на 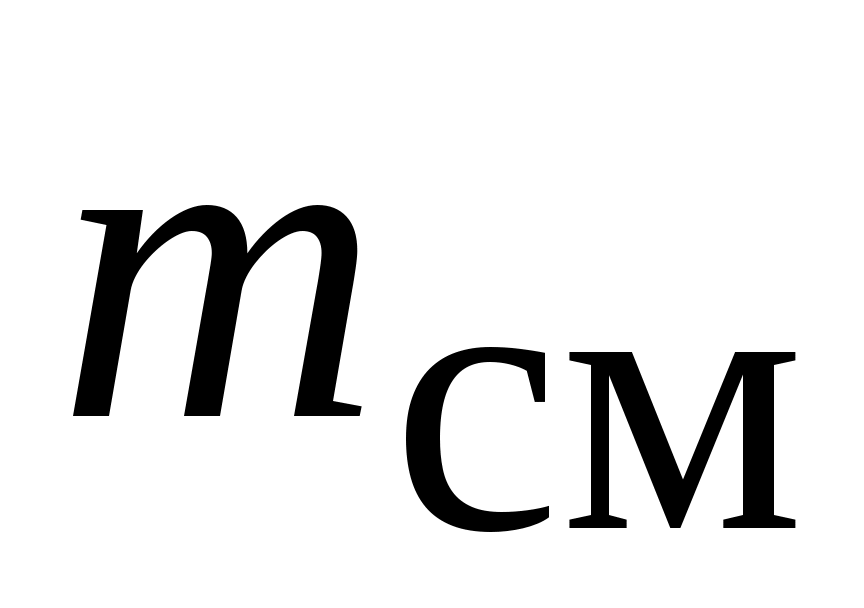 , получим , получим 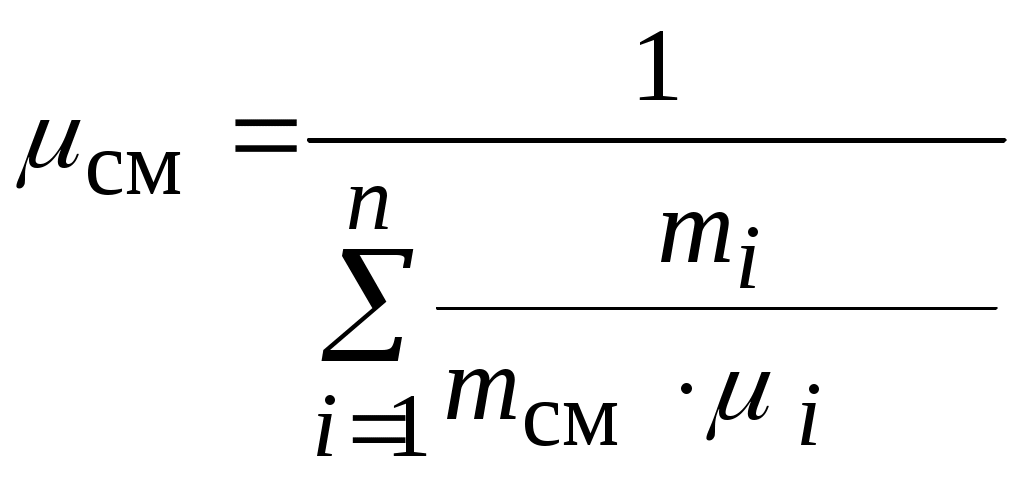 , ,
или окончательно
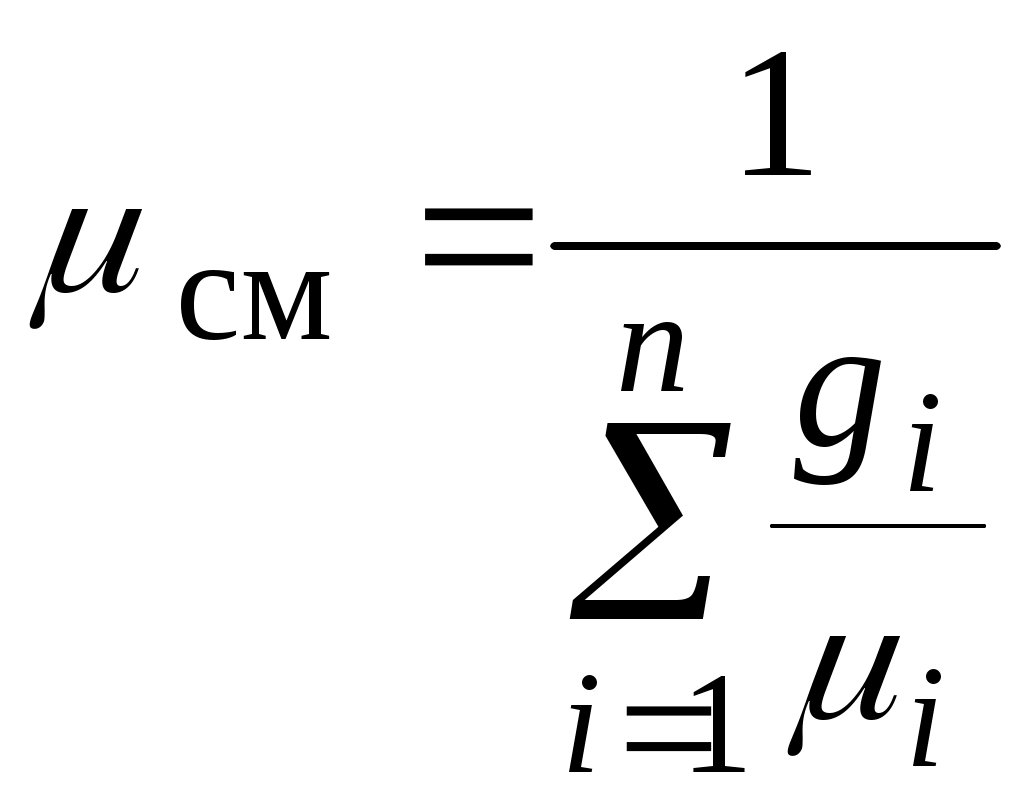
Через мольные доли величина 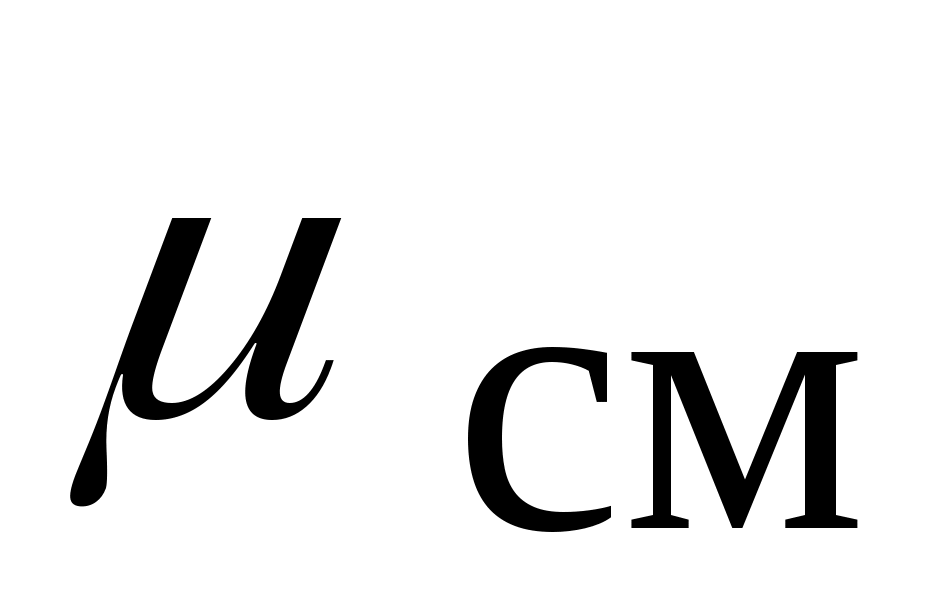 выражается проще: выражается проще:
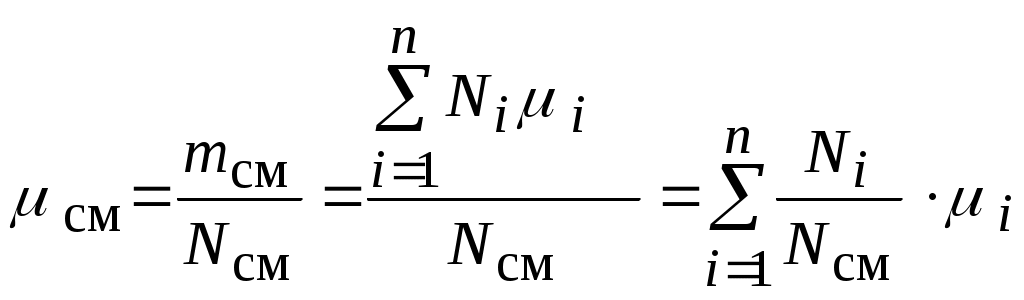 , ,
или окончательно
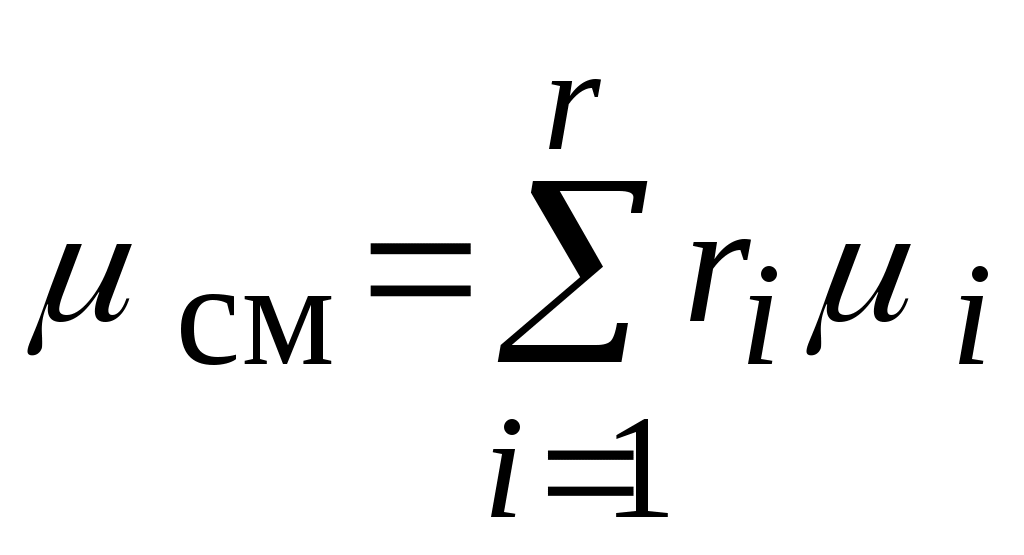
1.4.7. Газовая постоянная смеси газов
Удельная газовая постоянная однородного газа, заменяющего смесь, называется газовой постоянной смеси Rсм, Дж / (кг·К):
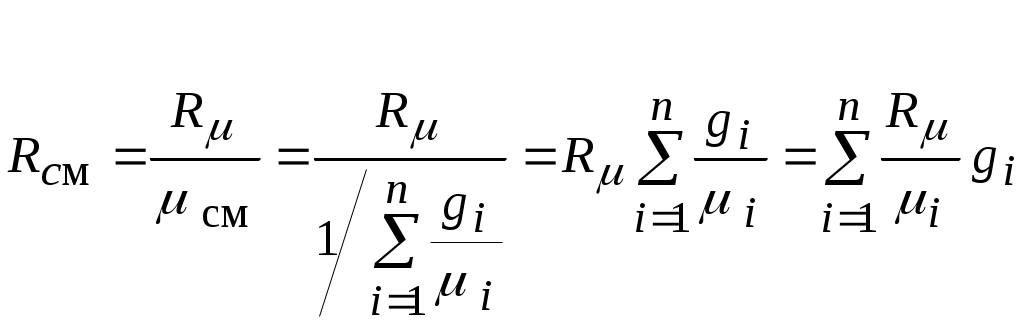 , ,
или окончательно
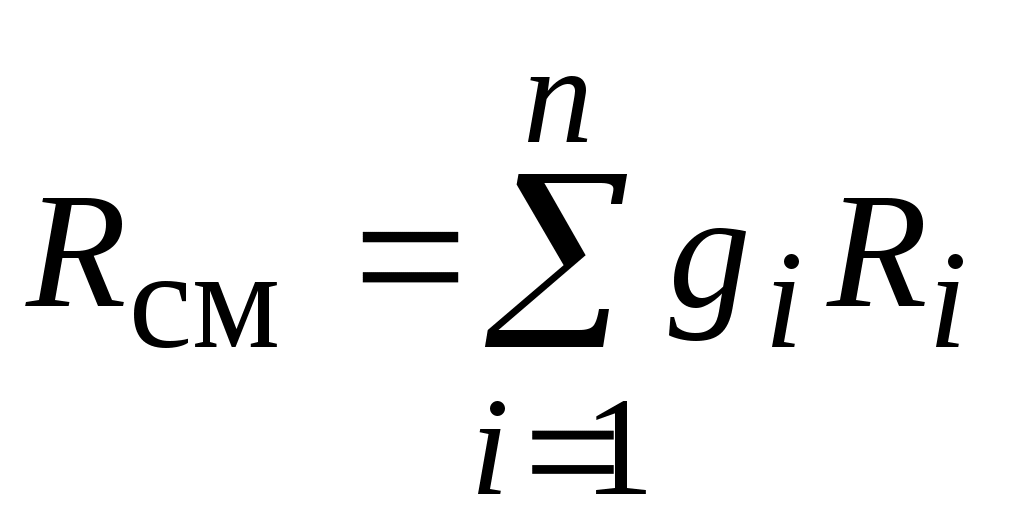 . .
Через мольные доли газовая постоянная смеси вычисляется следующим образом:
 , или окончательно , или окончательно
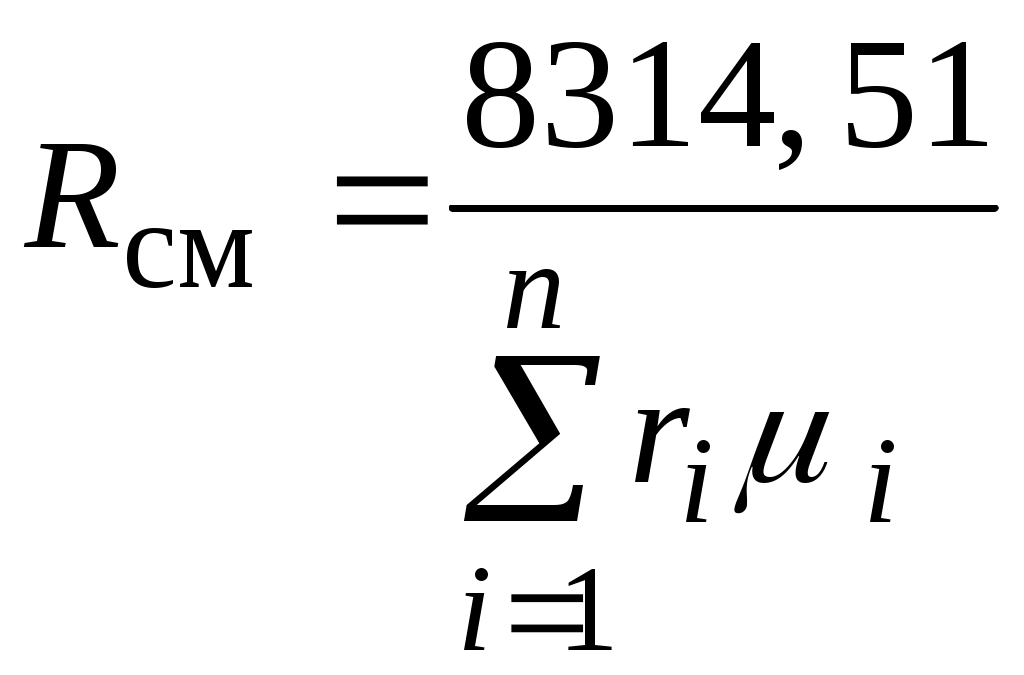 . .
С использованием 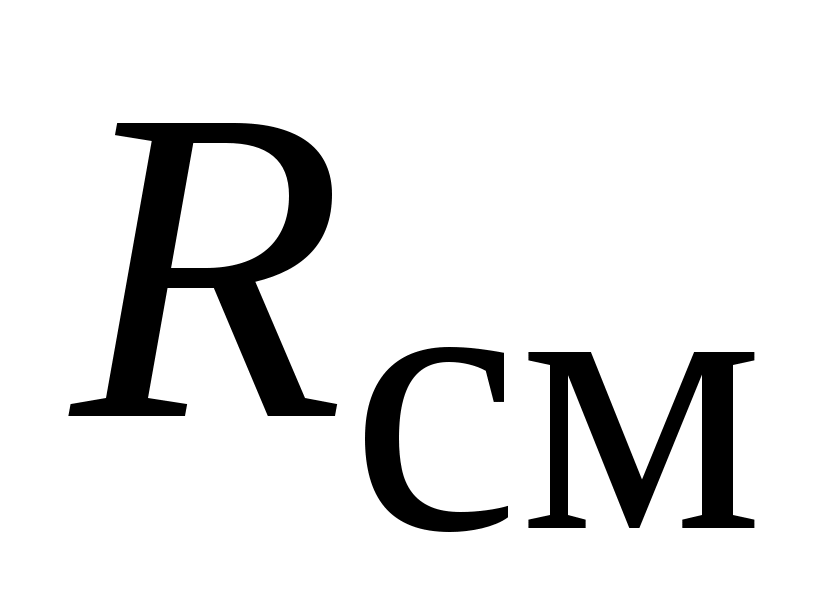 можно получить формулу для вычисления парциального давления идеального газа можно получить формулу для вычисления парциального давления идеального газа 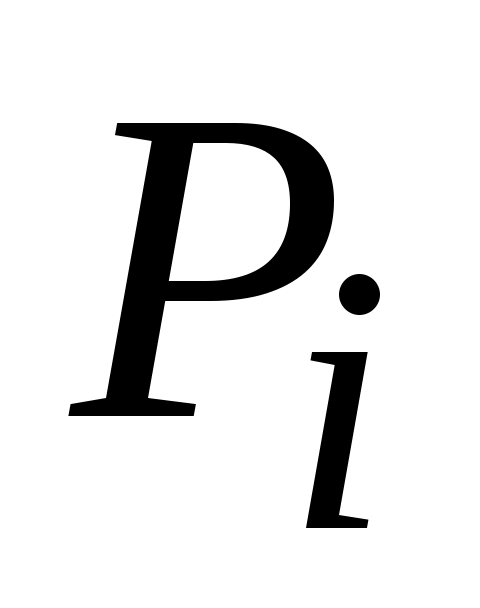 через его массовую долю. через его массовую долю.
Т. к. 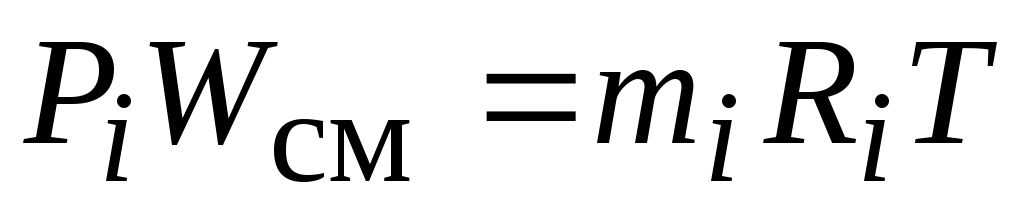 и и 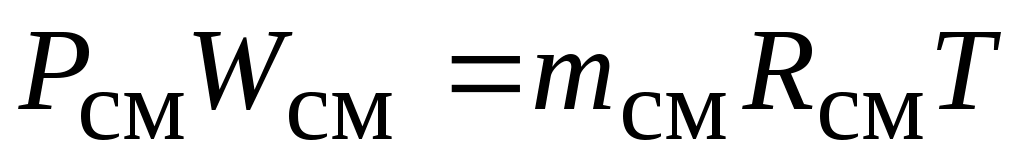 , ,
то разделив эти выражения друг на друга получим:
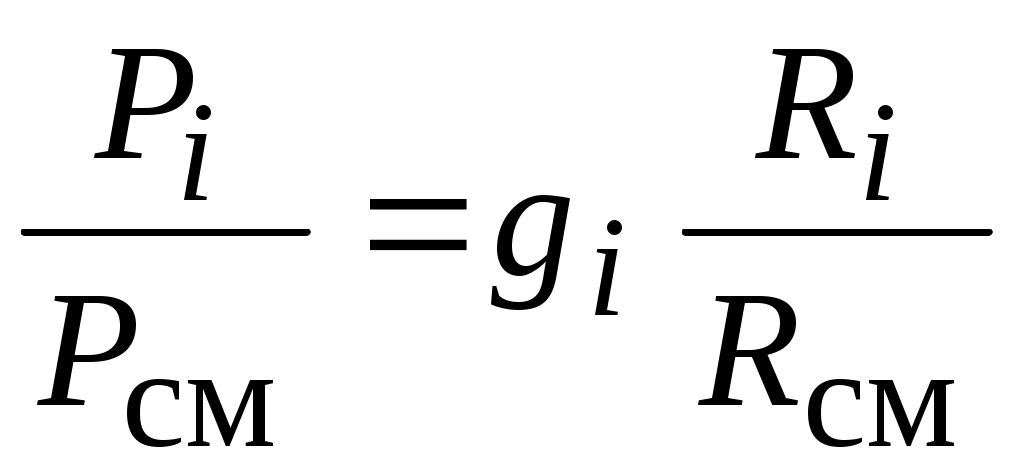 , ,
откуда 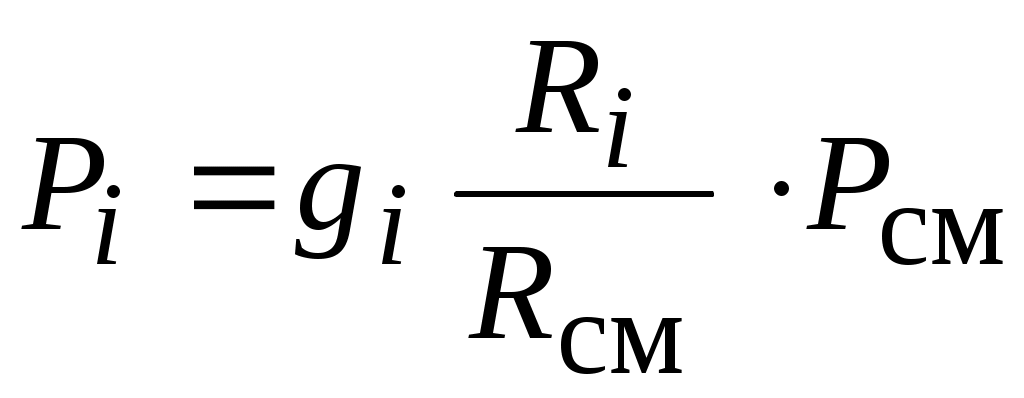
Из последнего выражения можно получить удобную формулу, связывающую мольные и массовые доли идеального газа.
Т. к. 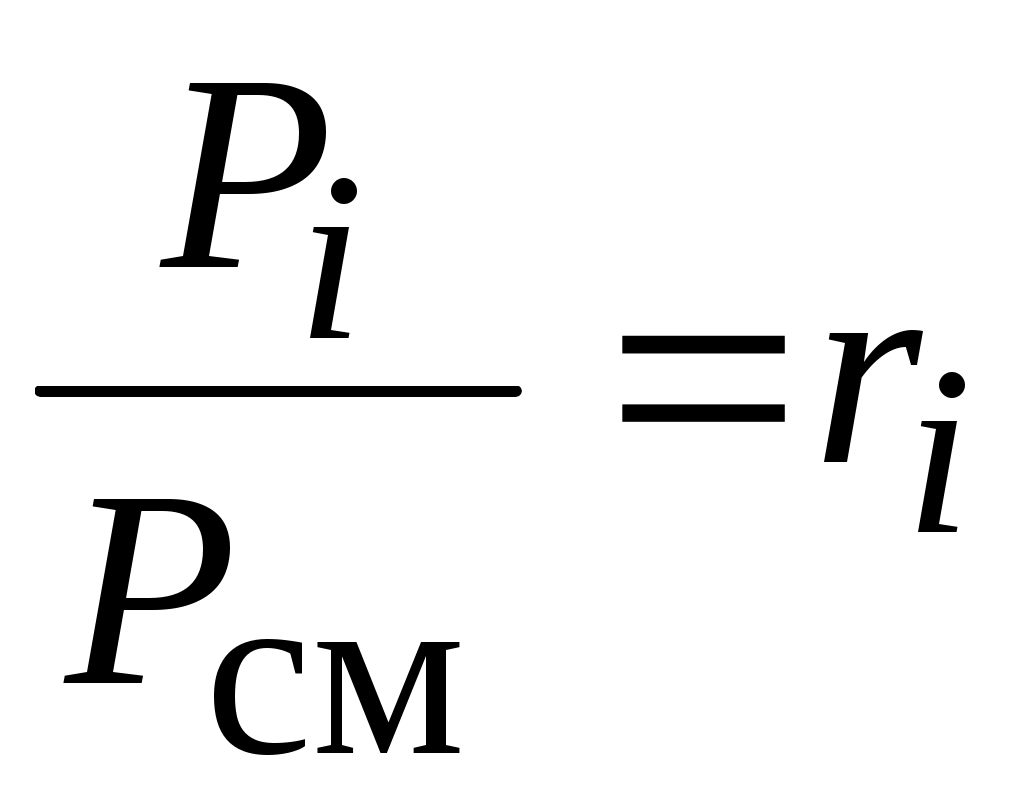 , ,
то 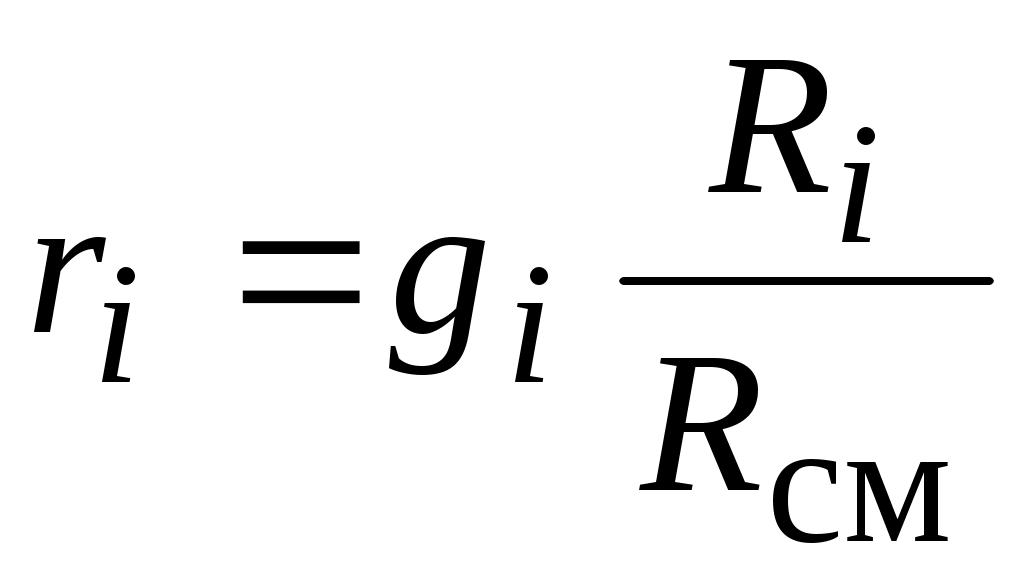
|
 Скачать 1.16 Mb.
Скачать 1.16 Mb.
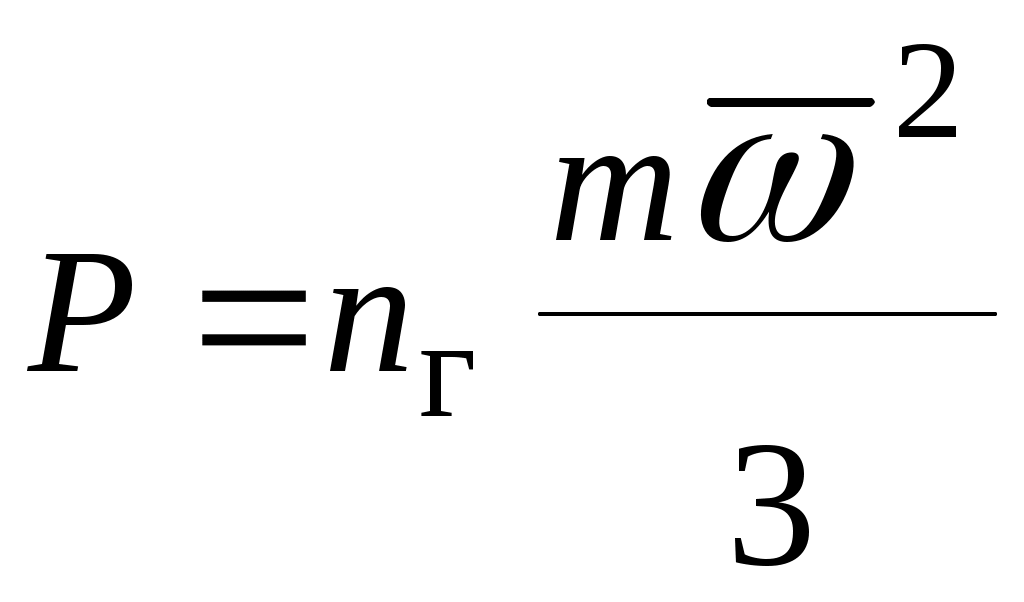 ,
,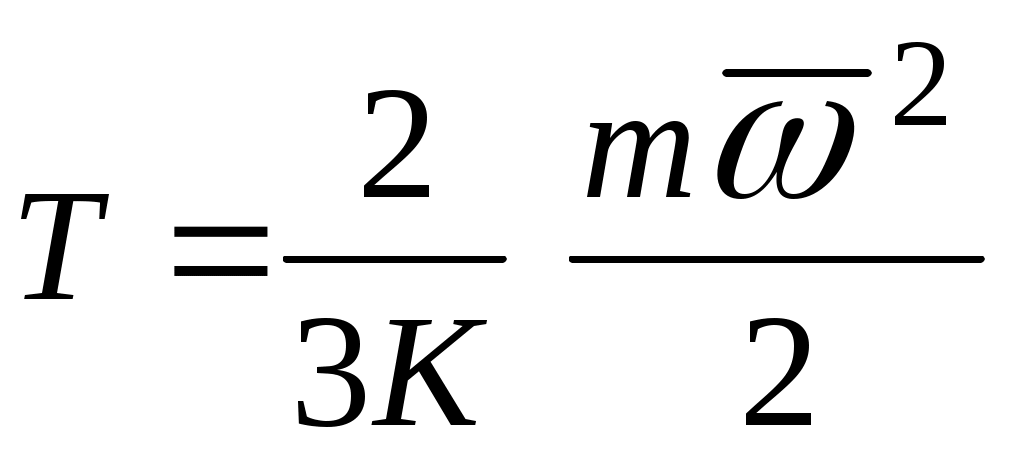 ,
,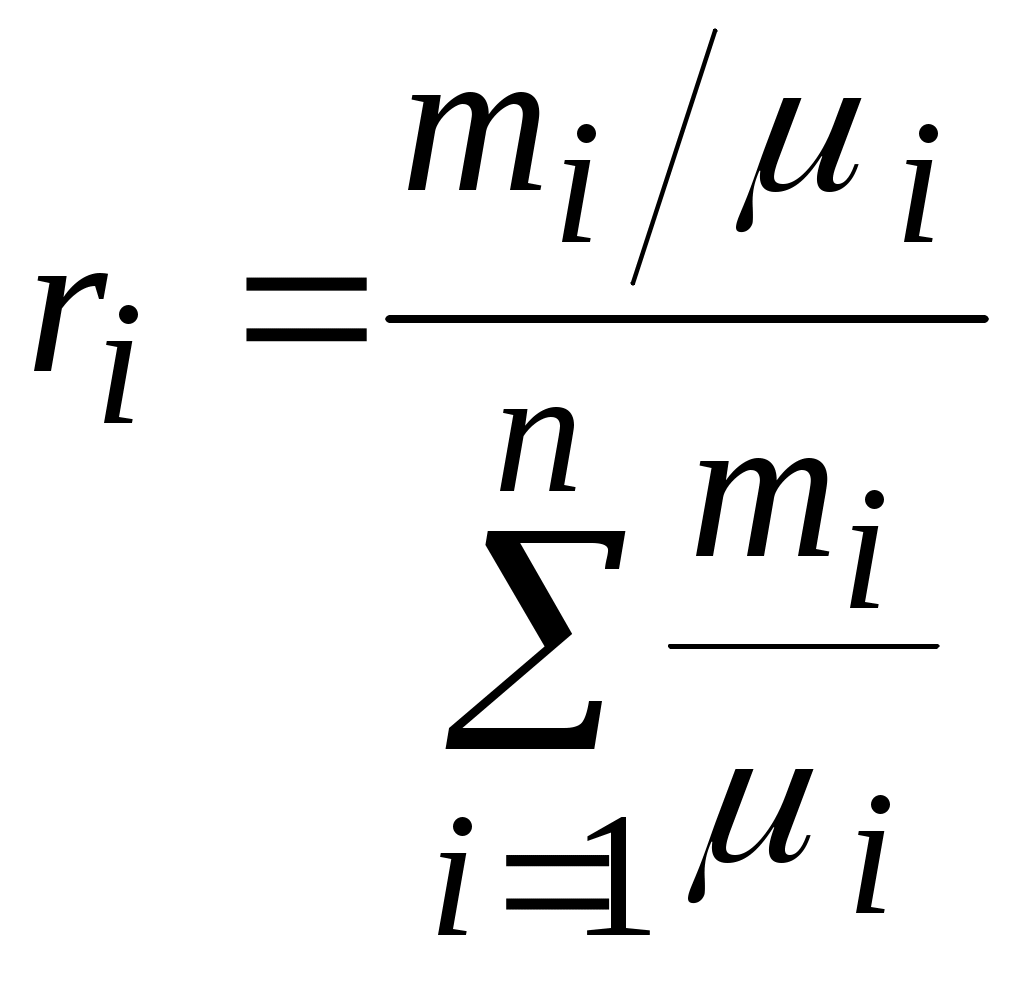 .
. 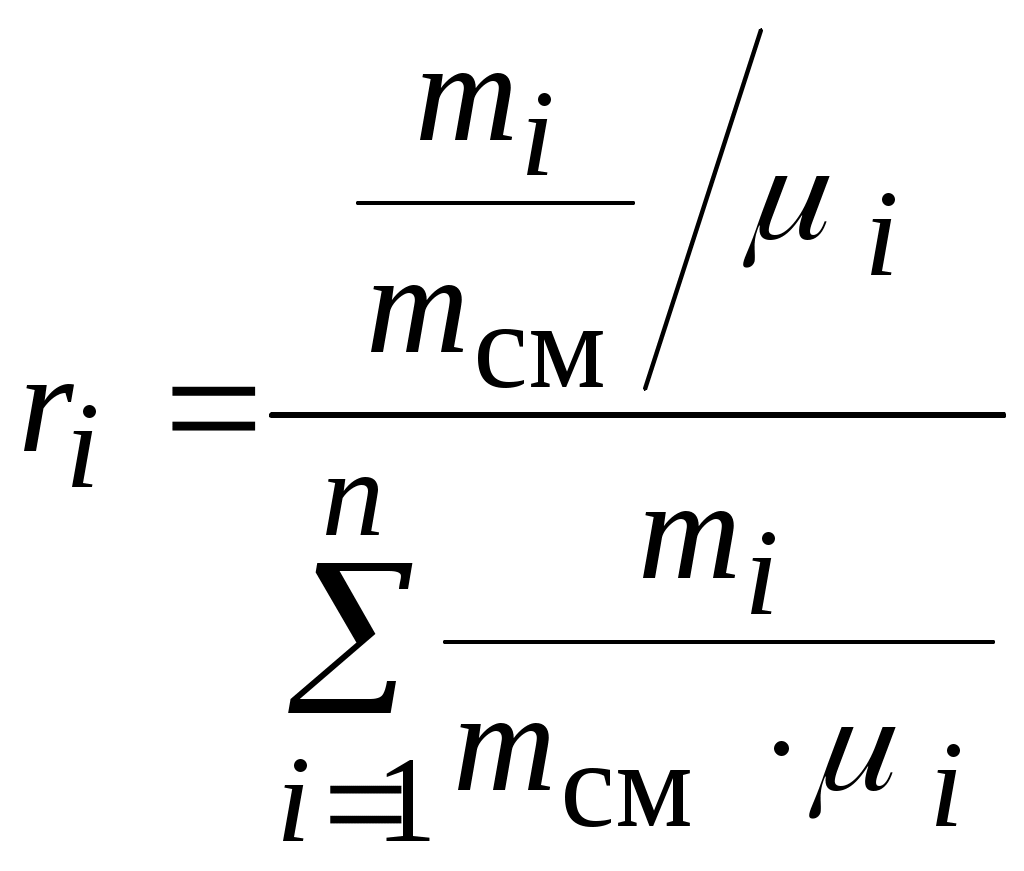 ,
, 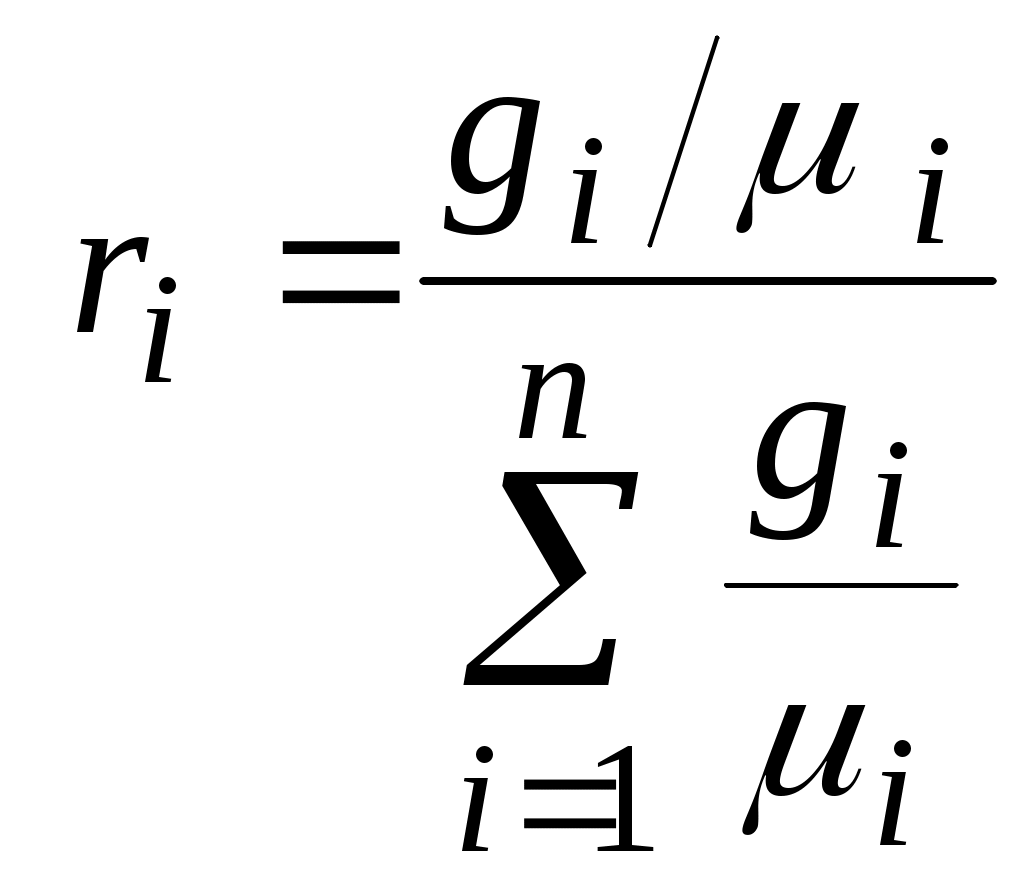
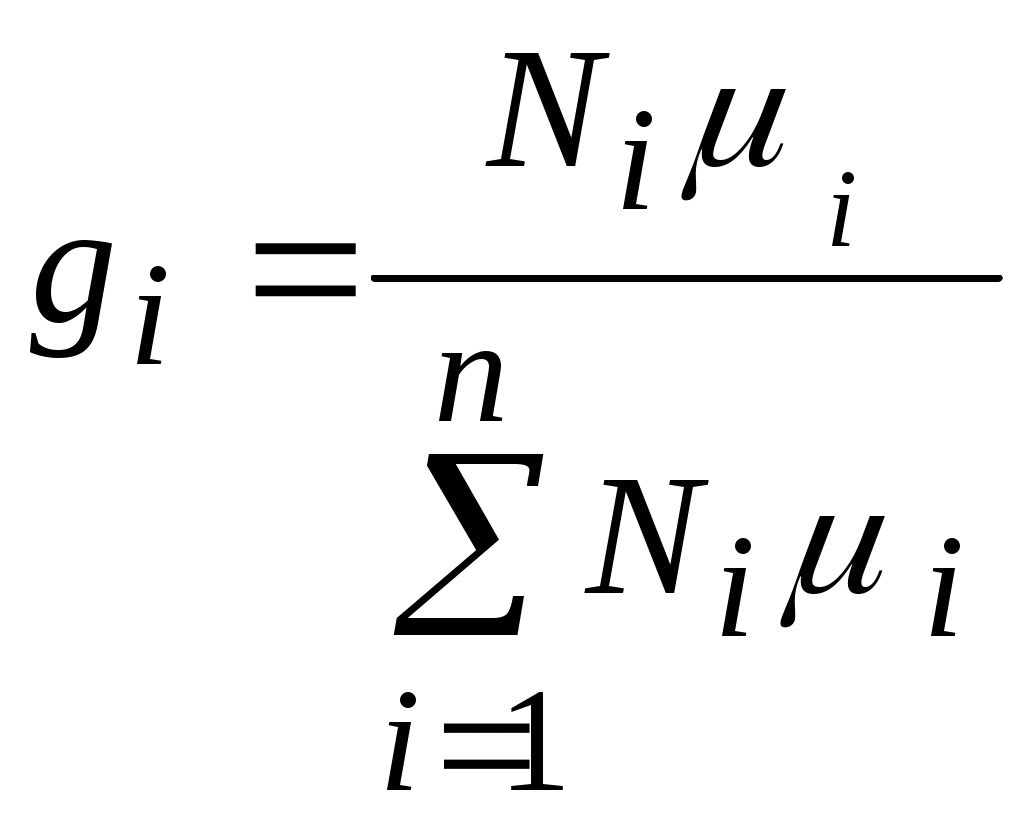 .
.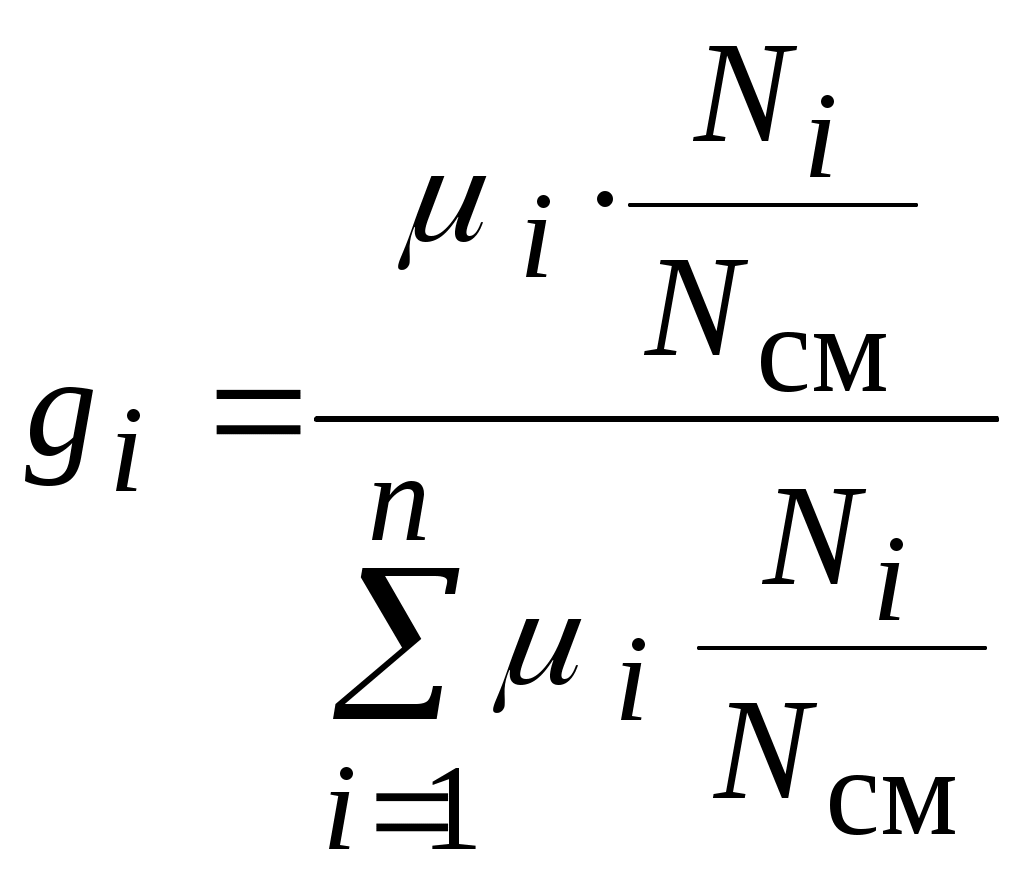 ,
,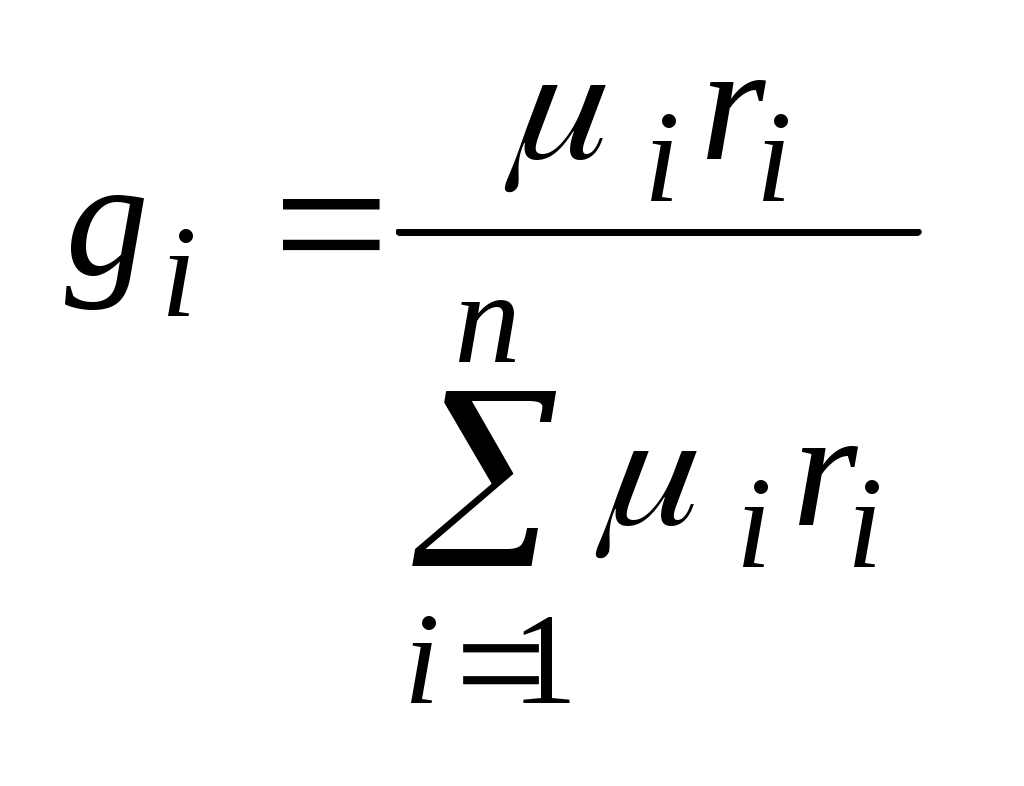
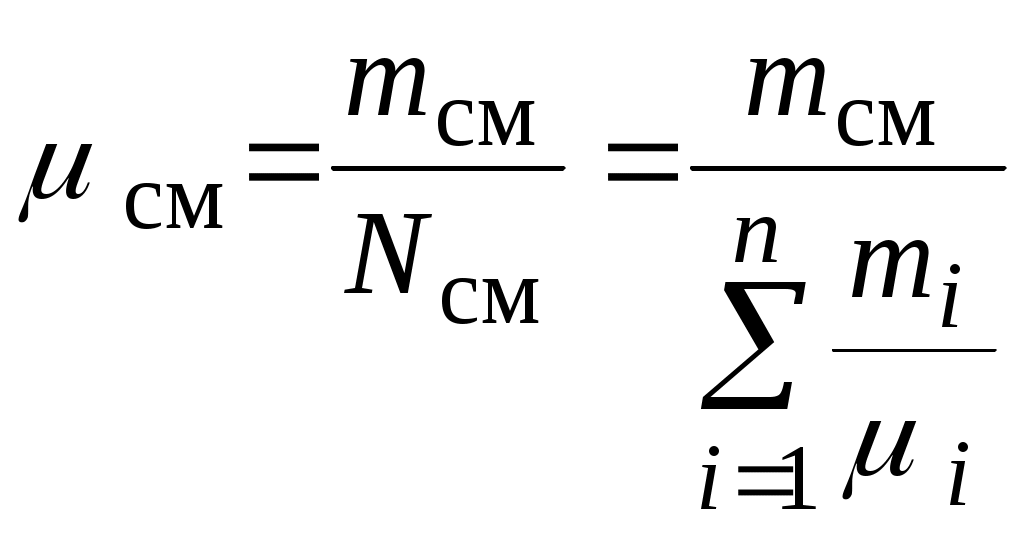 .
.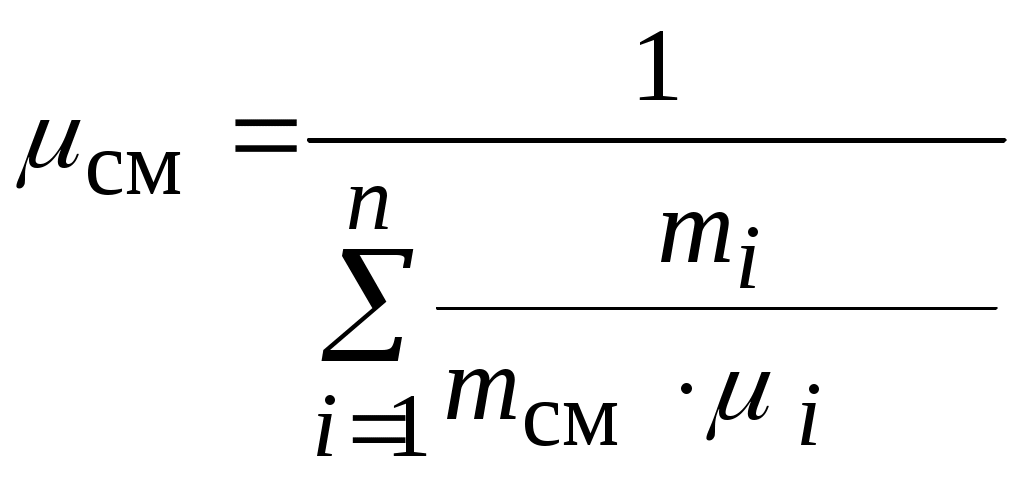 ,
, 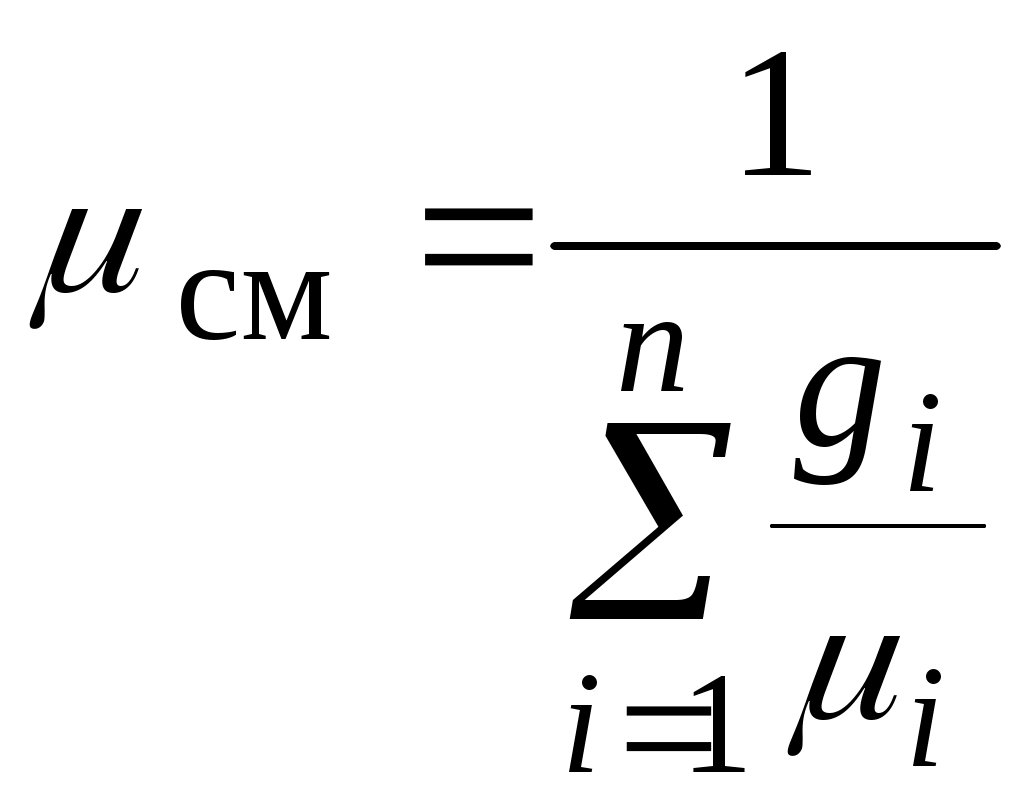
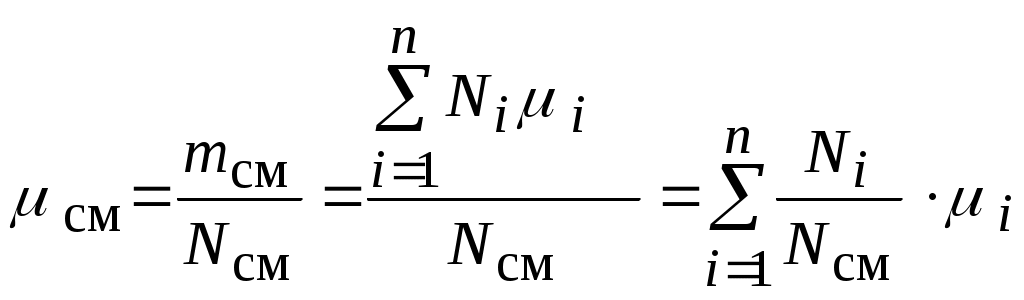 ,
,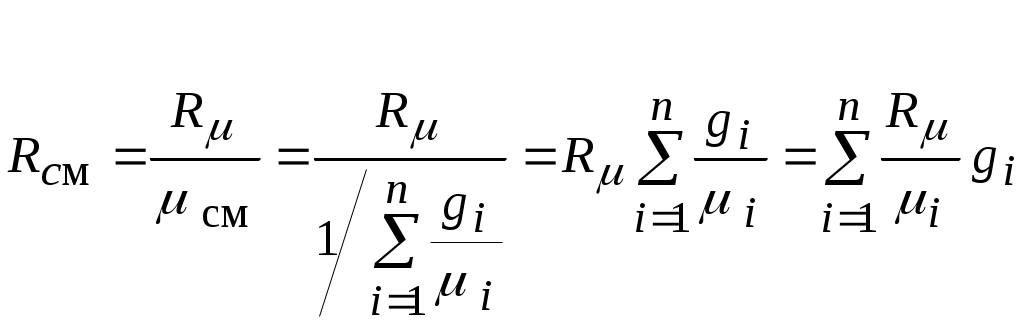 ,
, , или окончательно
, или окончательно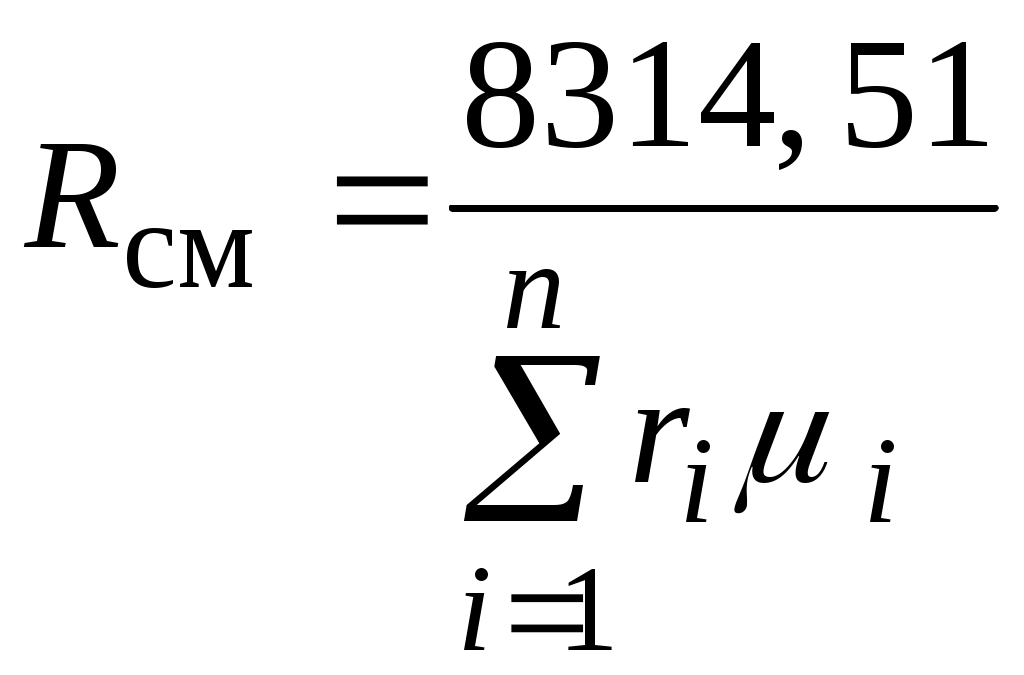 .
.