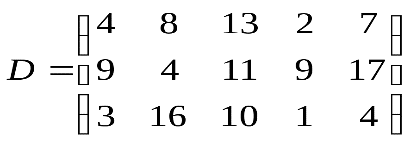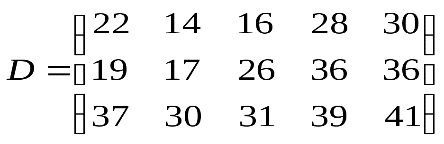Лабораторная работа. мат мод 28 исип1. Гбпоу "Чеченский государственный педагогический колледж" Поурочный план
 Скачать 133.34 Kb. Скачать 133.34 Kb.
|
ЗаверенЗам. директор по УМР________А.В. Самарская ГБПОУ "Чеченский государственный педагогический колледж"Поурочный план
Дисциплина: Математическое моделирование Тема: Лабораторная работа № 20«Построение простейших математических моделей. Построение простейших статистических моделей» (2ч) Тип урока:_практическое занятие Цели урока: а) образовательная: закрепить практические навыки по построению простейших математических и простейших статистических моделей. б) развивающая: обеспечение формирования у студентов профессиональных и общих компетенций. в) воспитательная: развитие логического мышления у студентов Ход урока 1. Организационный момент: приветствие, отметка присутствующих, подготовка к уроку, проверка психологической готовности к уроку 2. Повторение пройденного материала (опрос) Вопросы: Сформулировать определение презентации Где применяются презентации Слайд как формируется Способы создания презентации В какой программе мы может создать презентацию 3. Изложение нового материала (с приложением необходимого материала) Построение математической модели процесса, явления или объекта начинается с построения упрощенного варианта модели, в котором учитываются только основные черты. В результате прослеживаются основные связи между входными параметрами, ограничениями и показателем эффективности. Общего подхода к построению модели нет. В каждом конкретном случае при построении математической модели учитывается большое количество факторов: цель построения модели, круг решаемых задач, точность описания модели и точность выполнения вычислений. Математическая модель должна отражать все существенные факторы, определяющие ее поведение, и при этом быть простой и удобной для восприятия результатов. Каждая математическая модель процесса, явления или объекта в своей основе имеет математический количественный метод. Применение математических количественных методов для обоснования выбора того или иного управляющего решения во всех областях человеческой деятельности называется исследованием операций. Целью исследования операций является нахождение с использованием специального математического аппарата решения, удовлетворяющего заданным условиям. На самом деле при решении практически любой задачи имеется неограниченное количество решений. Множество решений, удовлетворяющих заданным условиям (ограничениям), называется допустимым множеством решением. Выбор из множества допустимых решений одного решения, наилучшего в каком-либо смысле, называемого оптимальным решением, и есть задача исследования операций. Модель — это материальный или идеальный объект, заменяющий оригинал, наделенный основными характеристиками (чертами) оригинала и предназначенный для проведения некоторых действий над ним с целью получения новых сведений об оригинале. 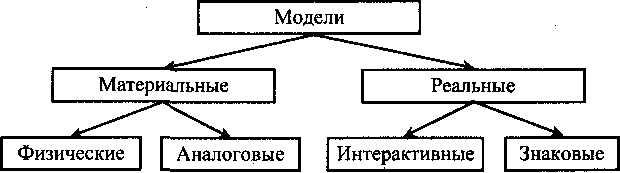 Рис. 1. Классификация моделей 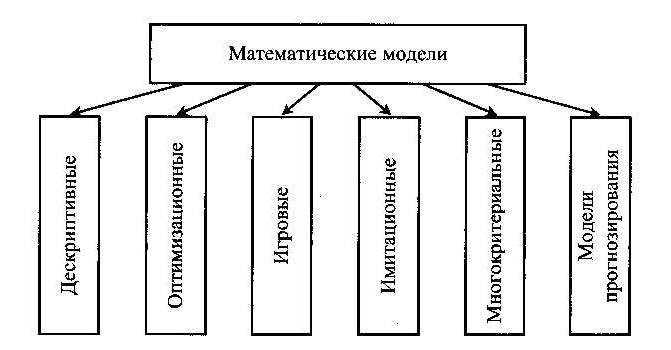 Рис. 2. Классификация математических моделей При построении математической модели необходимо обеспечить достаточную точность вычислений (точность решения) и необходимую подробность модели. Любая математическая модель включает в себя описание основных, т. е. необходимых для исследования свойств и законов функционирования исследуемого объекта, процесса или явления. В своей основе каждая математическая модель имеет целевую функцию, которая описывает функционирование реального объекта, процесса или явления. В зависимости от исследуемого (моделируемого) объекта, явления или процесса целевая функция может быть представлена одной функциональной зависимостью, системой уравнений (линейных, нелинейных, дифференциальных и т. д.), набором статистических данных и т. д. При работе с целевой функцией исследователь воздействует на нее через набор входных параметров (рис. 3).
Рис. 3. Обобщенная схема математической модели По способу реализации математические модели можно разделить следующим образом. 1. Линейное программирование. Математическая модель целиком (целевая функция и ограничения) описывается уравнениями первого порядка. Линейное программирование включает в себя несколько методов решения (задач): симплексный; графический; транспортная задача; целочисленное программирование. 2. Нелинейное программирование. Целевая функция и ограничения, составляющие математическую модель, содержат хотя бы одно нелинейное уравнение (уравнение второго порядка и выше). Нелинейное программирование содержит несколько методов решения (задач): графический; регулярного симплекса; деформируемого многогранника (Нелдера - Мида); градиентный. 3. Динамическое программирование. Ориентировано на решение задач прокладки магистралей кратчайшим путем и перераспределения различных видов ресурсов. 4. Сетевое планирование. Решает проблему построения графика выполнения работ, распределения производственных, финансовых и людских ресурсов. 5. Принятие решений и элементы планирования. В этом случае и качестве целевой функции выступает набор статистических данных или некоторые данные прогноза. Решением задачи являются рекомендации о способах поведения (стратегии). Решение носит рекомендательный характер (приблизительное решение). Выбор стратегии целиком остается за человеком — ответственным лицом, принимающим решение. Для принятия решения разработаны следующие теории: теория игр; системы массового обслуживания. Задание 1. Составить математическую модель следующей задачи. На складе имеется 300 кг сырья. Надо изготовить два вида продукции. На изготовление первого изделия требуется 2 кг сырья, а на изготовление второго изделия — 5 кг. Определить план выпуска двух изделий. Решение. Обозначим, х1 – единица первого изделия, х2 – единица второго изделия. Тогда составим математическая модель: 2х1+5х2=300. Задание 2. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал 3-х сортов. При этом на изготовление единицы изделия вида А расходуется 14 кг первого сорта, 12 кг второго сорта и 8 кг третьего сорта. На изготовление продукции вида В расходуется 8 кг первого сорта, 4 кг второго сорта, 2 кг третьего сорта. На складе фабрики имеется всего материала первого сорта 624 кг, второго сорта 541 кг, третьего сорта 376 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида 7 руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида 3 руб. Определить максимальную прибыль от реализации всей продукции видов А и В. Решение. Составим математическую модель задачи: Пусть х1 – единица готовой продукции вида А, x2 - единица готовой продукции вида В, Цель фабрики получить максимальную прибыль от реализации всей продукции видов А и В, тогда: Система ограничений:  Задание 3. Составить математическую модель следующей задачи. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве 200, 450, 250 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно 100, 125, 325, 250, 100 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:
Решение: Проверка сбалансированности модели задачи. Модель является сбалансированной, т.к. суммарный объем запасов сырья равен суммарному объему потребности в ней: 200+450+250=100+125+325+250+100. Построение математической модели – неизвестными в этой задачи является объем перевозок. Пусть Где Неизвестные в этой задачи должны удовлетворять следующим ограничениям: Объем перевозок не могут быть отрицательными; Поскольку модель сбалансирована, то вся продукция должна быть вывезена с предприятия, а потребность всех пунктов потребления должна быть полностью удовлетворены. Итак, имеем следующую задачу: Найти минимум функционала: + При ограничениях: 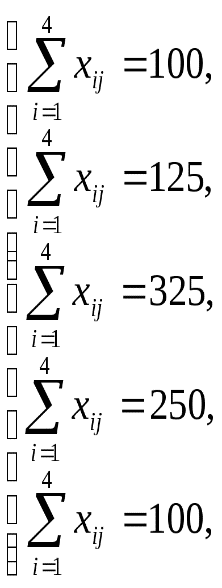  Задания для самостоятельной работы1 Вариант.Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 19, а2= 16, а3= 19, b1= 26, b2= 17, b3= 8, c1= 868, c2= 638, c3= 853, α=5, β=4. Задача 2. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.
2 Вариант.Задача 1. Составить математическую модель следующей задачи. Предположим, что для производства продукции вида А и В можно использовать материал трех сортов. При этом на изготовление единицы изделия вида А расходуется а1 кг первого сорта, а2 кг второго сорта и а3 кг третьего сорта. На изготовление продукции вида В расходуется b1 кг первого сорта, b2 кг второго сорта, b3 кг третьего сорта. На складе фабрики имеется всего материала первого сорта с1 кг, второго сорта с2 кг, третьего сорта с3 кг. От реализации единицы готовой продукции вида А фабрика имеет прибыль вида α руб., а от реализации единицы готовой продукции вида В фабрика имеет прибыль вида β руб. Определить максимальную прибыль от реализации всей продукции видов А и В. а1= 14, а2= 15, а3= 20, b1= 40, b2= 27, b3= 4, c1= 1200, c2= 993, c3= 1097, α=5, β=13. Задача 2. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4, b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в таблице:
Найти такой план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными.
4. Закрепление (с описанием заданий) Что такое модель? Приведите классификацию моделей. Какие вы знаете виды математических моделей? Дайте определение целевой функции. Что такое область допустимых решений? Что называется допустимым решением, оптимальным решением? Какие способы реализации математических моделей вы знаете? Что такое шаблон документа? Как создать и использовать созданный шаблон 5. Домашнее задание (с инструктажем о выполнении) 6. Подведение итогов (с комментированием оценок) 7. Рефлексия Все ли было вам понятно из изученного материала Какие моменты при объяснении материала вызвали затруднения в восприятии Преподаватель___________Хунарикова А.К. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||