ГЕЙМИФИКАЦИЯ НА УРОКАХ МАТЕМАТИКИ КАК СРЕДСТВО ПО-ВЫШЕНИЯ МОТИВАЦИИ. Статья 2. Геймификация на уроках математики как средство повышения мотивации
 Скачать 19.84 Kb.
|
|
ГЕЙМИФИКАЦИЯ НА УРОКАХ МАТЕМАТИКИ КАК СРЕДСТВО ПОВЫШЕНИЯ МОТИВАЦИИ Как известно, игровые технологии можно довольно широко использовать в качестве одного из средств развития, воспитания и, в том числе обучения. Увеличение умственной нагрузки на уроке побуждает учителя применять те или иные игровые приёмы для поддержания заинтересованности, и, как следствие, активности учащихся на уроке. Именно для этого многие педагоги ведут поиски новой методики обучения, различных приёмов, которые будут способствовать стимуляции самостоятельного приобретения знаний учениками. Ведь основной задачей учителя является развитие их познавательных способностей. Возникновение у учащихся интереса к изучаемому предмету и, в частности, к математике, как минимум на половину зависит от того, как будет построена методика преподавания. Задачей учителя является создание такой атмосферы, при которой как можно большая часть учеников работала активно, была заинтересована, настроена на познание. Как отметил В.Г. Коваленко, особенно это важно в подростковом возрасте, когда только формируются, только определяются постоянные интересы и склонности к той или иной учебной дисциплине [3]. Обучение математике не должно сводиться только лишь к сообщению каких-то фактов. Его цель — развитие интеллекта, культуры мышления, любознательности, дисциплинированности и критичности. И конечно же — математического мышления. В качестве эффективных средств развития интереса к учебному предмету принято использовать такие приёмы, как: логические разминки, дидактические игры, сюжетно-ролевые игры, творческие задания, ребусы [2]. Применение этих процессов вовлечения и мотивации учащихся в науке получило название «геймификация образования». Под геймификацией принято понимать применение игровых методик в неигровых ситуациях [1]. Как показывают исследования, использование игровых технологий позволяет оптимизировать образовательный процесс. Используя педагогическую литературу, можно выделить следующие случаи применения геймификации: в качестве фрагмента урока (его начала либо окончания); в качестве способа освоения какой-либо части предмета либо её закрепления; в качестве переходного элемента к следующей теме занятия; для внеурочной деятельности. Помимо этого встречаются и различные классификации игр, которые можно условно объединить в следующее группы: по цели обучения (воспитывающие, развивающие, обобщающие, контролирующие, обучающие); по характеру деятельности учащихся (творческие, поисковые, поисково-творческие); по массовости (коллективные, индивидуальные); по реакции (подвижные (быстрые), «тихие»). В настоящее время тему геймификации образования можно назвать довольно развитой. О применении тех или иных игровых технологий написано множество научных и методических работ, как зарубежных, так и отечественных исследователей и педагогов, таких как Д. Кларк, В. Г. Коваленко, Л. П. Варенина и др. Как известно, структурными компонентами игры являются: игровой замысел, правила, сами участники игры, цели и задачи, содержание и результат; так же, в частности, в математических дидактических играх компонентами будут являться оборудование (например, линейка, циркуль) и дидактическая задача. Сочетание всех элементов игры, их взаимодействие в совокупности повышают её эффективность и, как следствие, приводят к положительному результату. Какова же польза игры? Игра — это процесс, в котором участвуют две или более сторон, преследующих одну цель, однако конкурирующих между собой. Эти стороны следуют определённой, выработанной в большей части ими самими, стратегией, от выбора которой зависит победа или же поражение игрока. Таким образом, ключевым моментом в игре является дух соперничества. Задачей учителя является создание игрового сюжета, распределение ролей, а так же поддержание дисциплины. Ведь урок, построенный с использованием геймификации, будет полезен лишь в том случае, когда учащиеся дисциплинированы, внимательны, в меру активны и заняты самостоятельной работой. В случае, если все условия и правила игры будут выполнены верно, то она даст положительные результаты не только в обучении, но и в формировании личностных свойств, поскольку в этом случае будет реализован принцип воспитания в коллективе [3]. Пожалуй, одной из самых известных игр является «Морской бой». Однако, мало кому известно, что даже такую простую игру можно использовать в образовательных целях. Так, с помощью неё, ученики быстро могут освоить такую тему, как «координаты точки на плоскости». В процессе данной игры учащиеся убеждаются, что положение точки на плоскости определяется с помощью двух её координат, при этом система отсчёта у каждого игрока должна быть одинакова, для того, чтобы возможно было играть. Помимо способствования лёгкому усвоению математического материала, эта игра развивает также немало важные тактические навыки ученика: внимание, наблюдательность, сообразительность, терпение и выдержку. Всё это будет полезно не только на уроке математики, но и может пригодиться в жизни. Игрой, которая отлично подойдёт как для обучения математике, так и для тематической внеклассной работы можно назвать «Космическую прогулку». Основная цель игры — отработать умения и навыки применения правил умножения десятичных дробей; помимо этого игра должна осуществить контроль знаний учащихся, развить их любознательность и коммуникацию. Класс разбивается на 3 группы, каждая группа- экипаж космического корабля. У каждого ученика есть путевой лист, в котором он записывает результаты и решение всех примеров, встречающихся в течение урока. Игра состоит из 3-х этапов: составление девиза урока, расчёта пути планет и расчёта площади посадочной полосы. На 1-м этапе учащиеся должны восстановить слова В. Чкалова «Полёт — это математика», решив следующие примеры и записав ответы в таблицу: 2,5·0,3=0,75(П) 10) 1,5·0,8=1,2(А) 1,2·4=4,8(О) 11) 3700·0,01=37(Т) 7·0,8=5,6(Л) 12) 100·0,1=10(Е) 2,1·0,01=0,021(Ё) 13) 20,8·0,2=4,16(М) 3,7·10=37(Т) 14) 4·0,3=1,2(А) 5,4·0,02=0,108(Э) 15) 74·0,5=37(Т) 0,37·100=37(Т) 16) 7,5·1,6=12(И) 20·0,24=4,8(О) 17) 0,4·1,04=0,056(К) 1,3·3,2=4,16(М) 18) 6·0,2=1,2(А) Таблица 1
На 2-м этапе учащиеся должны решить задачу: скорость планеты Меркурий 47,8км/с, а скорость планеты Венера на 12,8 км/с меньше. Какой путь проходит Меркурий за 3 с, а Венера за 10,2 с? Решение: 47,8-12,8=35 (км/с) – скорость планеты Венера 47,8·3=143,4 (км) — проходит планета Меркурий за 3 с. 10,2·35=357 (км)- проходит планета Венера за 10,2 с. Ответ: 143,4 км, 357 км. На 3-м этапе ученики должны «посадить» космический корабль, рассчитав периметр и площадь посадочной площадки, которая является квадратом со стороной, равной 2,3 км Решение: Р= 2,3·4=9,2(км), S= 2,3·2,3=5,29 ( 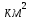 ) После этого происходит проверка ответов и самостоятельная оценка работ. Побеждает команда, решившая задания быстрее соперников и с меньшим количеством ошибок. Следует отметить, что данная игра многофункциональна, при усложнении условий и примеров в ней могут решаться задачи на повторение иных, более сложных математических тем. Таким образом, геймификацию нельзя назвать исключительно средством развлечения. Напротив, правильное применение игровых технологий позволяет создать такой феномен, когда игра, являясь развлечением, перерастёт в творчество, моделирование отношений и самое главное- обучение. К сожалению, из педагогического опыта известно, что возможности применения тех или иных игровых технологий до сих пор в полной мере не используются, недооцениваются преподавателями. А если и применяются, то в основном на занятиях математического кружка. Хочется верить, что со временем применение игровых технологий станет обычным явлением на уроках как математики так и иных образовательных дисциплин. Литература: Варенина Л. П. Геймификация в образовании// Историческая и социально-образовательная мысль. – 2014. – № 6–2, с. 314. Горнобатова Н. Н. Развитие познавательного интереса на уроках математики // Эксперимент и инновации в школе; № 2/2014, С. 33. Коваленко В. Г. Дидактические игры на уроках математики: Кн. Для учителя. – М.: Просвещение, 1990. – 96 с.: ил. – ISBN 5–09–002716–1; С. 3, 11. |