генеральная выборка. Генеральная и выборочная средние. Генеральная и выборочная средние. Методы их расчета
 Скачать 110.42 Kb.
|
|
Генеральная и выборочная средние. Методы их расчета Пусть изучается дискретная генеральная совокупность объема N относительно количественного признака X. Определение: Генеральной средней  (или а) называется среднее арифметическое значений признака генеральной совокупности.Если все значения  признака генеральной совокупности объема N различны, то Если же значения признака  имеют соответственно частоты  причем  то или  Как уже отмечалось (п. 1), извлечение объекта из генеральной совокупности есть наблюдение случайной величины X. Пусть все значения  различны. Так как каждый объект может быть извлечен с одной и той же вероятностью 1/N, то т. е.  Такой же итог следует, если значения  имеют соответственно частоты  В случае непрерывного распределения признака X по определению полагают  Пусть для изучения генеральной совокупности относительно количественного признака X произведена выборка объема n. Определение: Выборочной средней  , называется среднее арифметическое значений признака выборочной совокупности.Если все значения  признака выборки объема n различны, то Если же значения признака  имеют соответственно частоты  причем  , то или  Пример: Выборочным путем были получены следующие данные о массе 20 морских свинок при рождении (в г): 30, 30, 25, 32, 30, 25, 33, 32, 29, 28^27, 36, 31, 34, 30, 23, 28, 31, 36, 30. Найдем выборочную среднюю  Согласно формуле (4.4), имеем:  Итак,  Далее, не уменьшая общности рассуждений, будем считать значения  признака различными.Разумеется, выборочная средняя для различных выборок того же объема n из той же генеральной совокупности будет получаться, вообще говоря, различной. И это не удивительно — ведь извлечение і-го по счету объекта есть наблюдение случайной величины  а их среднее арифметическое есть тоже случайная величина. Таким образом, всевозможные получающиеся выборочные средние есть возможные значения случайной величины  , которая называется выборочной средней случайной величиной.Найдем  , пользуясь тем, что  (см. п. 1).С учетом свойств математического ожидания (см. гл. II) получаем:  Итак,  (математическое ожидание выборочной средней) совпадает с а (генеральной средней).Теперь найдем 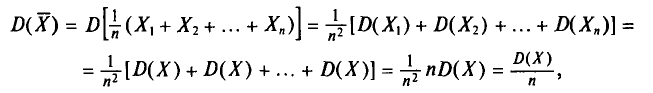 Так как  (п. 1) и  независимы, то, согласно свойствам дисперсии (см. гл. II), получаем T. e.  Наконец, отметим, что если варианты  —больши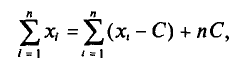е числа, то для облегчения вычисления выборочной средней применяют следующий прием. Пусть С — константа.Так как  то формулу (4.3) можно преобразовать к виду 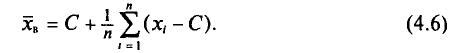 За константу С (так называемый ложный нуль) берут некоторое среднее значение между наименьшим и наибольшим значениями х, (і- 1, 2, …, n). Пример: Имеется выборка: 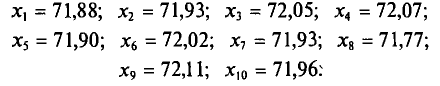 Требуется найти  Возьмем С =72,00 и вычислим разности 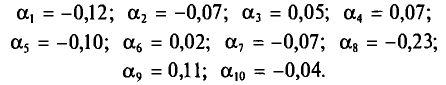  Их сумма:  их среднее арифметическое Выборочная средняя |