КондратьєваПотрійні. геометричні та механічні застосування потрійного інтеграла
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
2.3 Геометричні застосування потрійного інтеграла Геометричні застосування потрійного інтегралу випливають із геометричного змісту потрійного інтегралу. Якщо функція 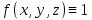 (тотожно дорівнює), тоді потрійний інтеграл (тотожно дорівнює), тоді потрійний інтеграл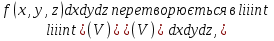 який дорівнює об’єму тіла, обмеженого областю (V). Отже, об’єм тіла 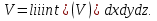 Також важливим геометричним застосуванням потрійного інтеграла є застосування формули Остроградського для представлення об’єму тіла за допомогою поверхневих інтегралів. Формула Остроградського — формула, що виражає потік векторного поля через замкнену поверхню через інтеграл від дивергенції цього поля по об'єму, замкнутий під поверхнею. Відомо, що за допомогою криволінійних інтегралів можна виразити площу, тому так само можна виразити і об’єм. А саме: можна різними способами підібрати функції P, Q, R так, що цей інтеграл зведеться до об’єму тіла (V). Таким чином, об’єм V представиться у вигляді поверхневого інтеграла, розповсюдженого на поверхню (S), яка обмежую тіло (V). Тоді, 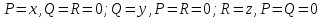 перейдемо до формул перейдемо до формул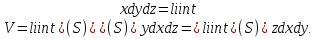 до того ж, всі інтеграли взяті по зовнішній стороні поверхні (S). Зручною є більше симетрична формула, коли 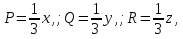 вона має вигляд: вона має вигляд: 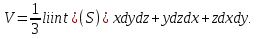 Приклад 6. Знайти потік векторного поля 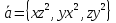 через замкнену поверхню через замкнену поверхню 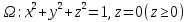 у напрямку зовнішньої нормалі. у напрямку зовнішньої нормалі.Розв’язування. Поверхня 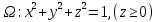 являє собою напівсферу, яка розміщена над площиною Oxy. Враховуючи те, що поверхня замкнена, скористуємося формулою Остроградського-Гауса: являє собою напівсферу, яка розміщена над площиною Oxy. Враховуючи те, що поверхня замкнена, скористуємося формулою Остроградського-Гауса: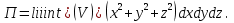 Перейдемо до сферичної системи координат 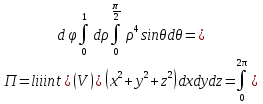 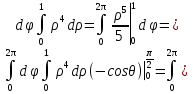 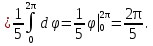 Відповідь: 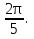 Приклад 7. Обчислити об’єм тіла, обмеженого поверхнями: 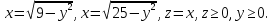 Розв’язування. Напишемо межі інтегрування, враховуючи (Мал. 2.4) 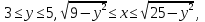 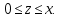 Мал. 2.10 Знайдемо об’єм через потрійний інтеграл:  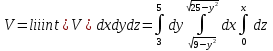 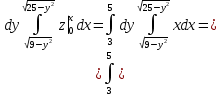 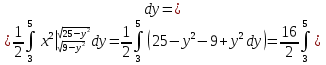 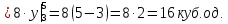 Відповідь: 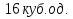 Приклад 16. Знайти об’єм тіла, обмеженого поверхнями 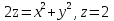 Розв’язування. Дане тіло обмежене знизу параболоїдом 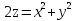 , зверху площиною , зверху площиною 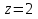 і проектується в круг і проектується в круг 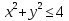 площини Oxy. Використовуючи циліндричні координати, знаходимо рівняння параболоїда площини Oxy. Використовуючи циліндричні координати, знаходимо рівняння параболоїда 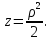 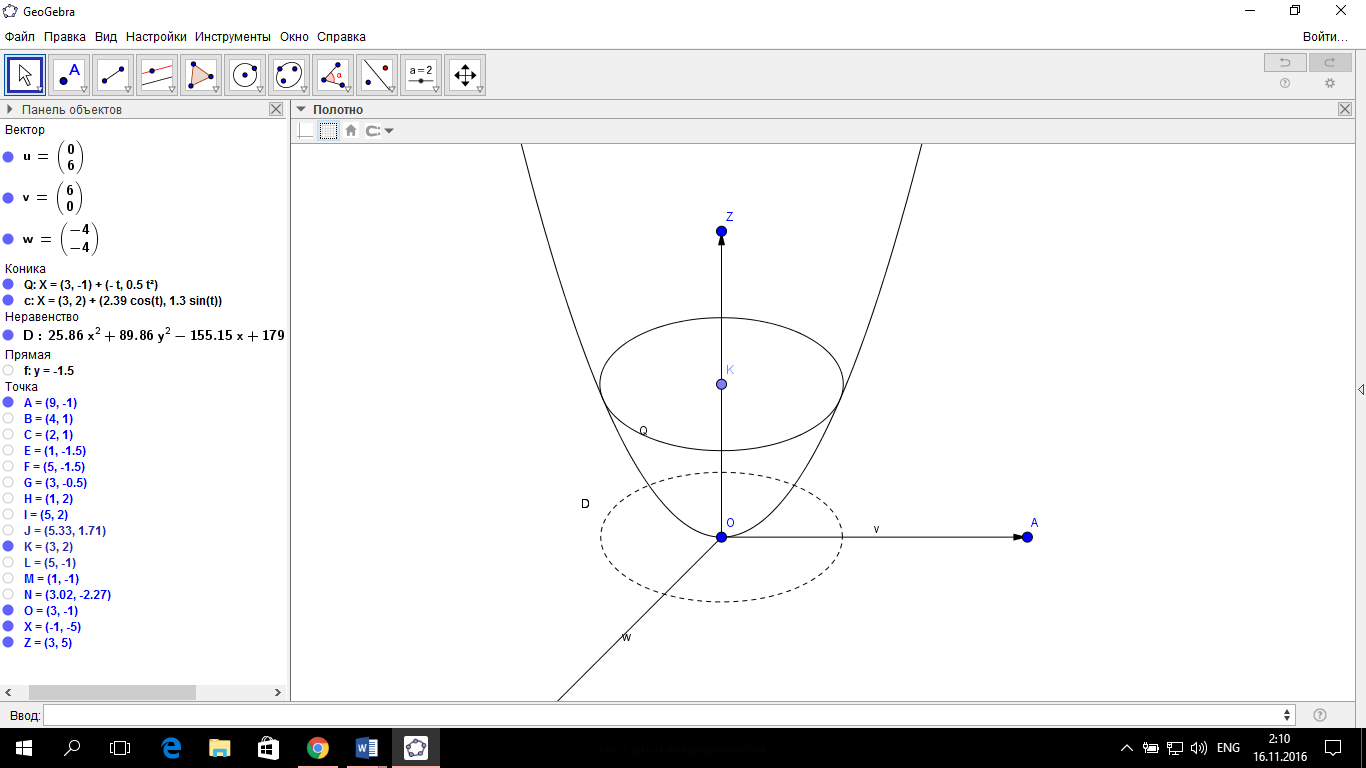 Мал. 2.11 Тоді: 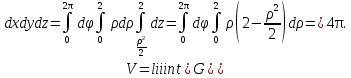 Відповідь: 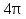 куб.од. куб.од.Приклад 9. Обчислити об’єм тіла, обмеженого еліпсом 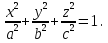 Розв’язування. За умови такого задання еліпса варто перейти до сферичних координат за формулами: 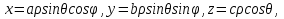  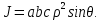 Рівняння поверхні в нових координатах : 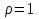 , тому для цього тіла , тому для цього тіла 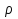 змінюється від 0 до 1. Тоді змінюється від 0 до 1. Тоді 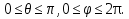 Тоді: 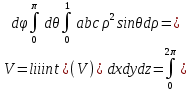 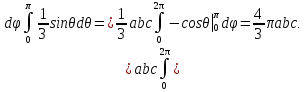 Розглянувши частинний випадок, коли 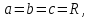 отримаємо об’єм кулі отримаємо об’єм кулі V= 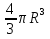 . .ВИСНОВКИ У ході курсової роботи я проаналізувала властивості та методи розв’язування потрійних інтегралів та розкрила їх геометричні та механічні застосування, розглянула визначення потрійного інтегралу запропонованих різними математиками, розглянула найцікавіші приклади розв’язування задач з геометрії та механіки. Застосування потрійних інтегралів залишається актуальною темою для дослідження. Геометричне застосування потрійного інтегралу не зупиняється на пошуку об’ємів тіл. Також важливим моментом є формула Остроградського, яка пов’язує потрійний інтеграл на просторі з поверхневим інтегралом по контуру області. Механічні застосування потрійного інтегралу, зокрема, маса і центр маси; координати центра маси; моменти інерції відносно координатних осей знаходять своє застосування в задачах з фізики. Моменти інерції відносно осі відіграють важливу роль при обчисленні кінетичної енергії тіла при його обертанні навколо відповідної осі. Кінетична енергія системи точок визначається як сума кінетичних енергій окремих точок, а кінетична енергія тіла – як сума кінетичних енергій всіх частин , на які воно було розбите. Ця обставина дозволяє застосовувати для обчислення кінетичної енергії потрійний інтеграл. ЛІТЕРАТУРА
ХАРКІВ – 2016 |
