КондратьєваПотрійні. геометричні та механічні застосування потрійного інтеграла
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ ІМЕНІ Г.С. СКОВОРОДИ ФІЗИКО-МАТЕМАТИЧНИЙ ФАКУЛЬТЕТ КАФЕДРА МАТЕМАТИКИ КУРСОВА РОБОТА На тему: «ГЕОМЕТРИЧНІ ТА МЕХАНІЧНІ ЗАСТОСУВАННЯ ПОТРІЙНОГО ІНТЕГРАЛА» Підготувала Студентка 3-го курсу Групи 3МФ Кондратьєва Тетяна Науковий керівник: доц. Долгова О.Є. ЗМІСТ ВСТУП РОЗДІЛ I. Потрійні інтеграли
РОЗДІЛ II. Практичне застосування
ВИСНОВКИ ЛІТЕРАТУРА ВСТУП Витоки інтегрування простежуються ще в давньому Єгипті, приблизно у 1800 до н.е. Першим відомим методом для розрахунку інтегралів є метод вичерпання Евдокса (приблизно 370 до н. е.), який намагався знайти площі і об'єми, розриваючи їх на нескінченну безліч частин, для яких площа або об'єм вже відомий. Значний прогрес у обчисленні інтегралів відбувається в XVI столітті. У роботах Кавальєрі з його методом неподільних, а також у роботах Ферма, були закладені основи сучасного інтегрального числення. Подальші кроки були зроблені на початку XVII століття Барроу і Торрічеллі, які вказали на зв'язок між інтегруванням і диференціюванням. Голландський механік, математик і фізик Х. Гюйгенс (1629-1695), у зв’язку з винайденим ним маятниковим годинником, ввів поняття моменту інерції тіла. Сам термін “момент інерції” запропонував Л. Ейлер (1707-1783). Поняття інтеграла та інтегральне числення виникли з потреби обчислювати площі (квадратуру) будь-яких фігур і об’єму (кубатуру) довільних тіл. Саме для обчислення об’єму тіла використовується потрійний інтеграл. Потрійний інтеграл є узагальненням подвійного інтеграла на випадок просторової області. До потрійного інтегралу приводить багато задач механіки та геометрії. До таких задач відносяться: знаходження статичних моментів тіла відносно координатних площин, знаходження координат центру маси тіла, моментів інерції тіла, обчислення об’ємів тіл. Геометричний зміст потрійного інтеграла реалізується за рахунок обчислення об’єму фігур, а також за рахунок представлення об’єму тіла за допомогою поверхневих інтегралів, що, в свою чергу, застосовується для обчислення потоку векторного поля. Мета курсової роботи: розглянути практичне застосування потрійного інтегралу у геометрії та механіці. У ході курсової роботи ми маємо виконати такі завдання:
РОЗДІЛ I. Потрійні інтеграли
В.А. Зорич дає більш загальне поняття інтегралів для будь-якої розмірності. Щоб підкреслити, що мова йде про інтеграл по багатовимірному простору І, кажуть, що це кратний інтеграл (маючи на увазі – подвійний, потрійний і т.д. у відповідності з розмірністю І). Розглянемо узагальнене визначення інтегралу для будь-якої розмірності. Проміжок в Rn і його міра. Означення 1. Множина І = 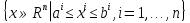 називається проміжком або координатним паралелепіпедом в називається проміжком або координатним паралелепіпедом в 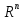 . Іноді, якщо треба відмітити проміжок точками . Іноді, якщо треба відмітити проміжок точками 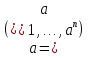 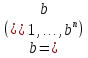 , то його часто позначають символом , то його часто позначають символом 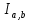 . . Означення 2. Проміжку 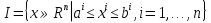 ставиться у відповідність число ставиться у відповідність число 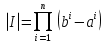 , яке називається об’ємом або мірою проміжка. Об’єм(міру) проміжка І позначають символами , яке називається об’ємом або мірою проміжка. Об’єм(міру) проміжка І позначають символами 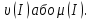 Лема 1. Міра проміжка в 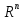 а) однорідна, тобто якщо 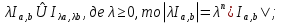 б) адитивна, тобто якщо проміжки І, І1, … ІK такі, що 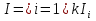 і проміжки І1,…, Іk попарно не мають спільних внутрішніх точок, тоді і проміжки І1,…, Іk попарно не мають спільних внутрішніх точок, тоді 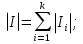 в) якщо проміжок І покритий скінченною системою проміжків 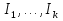 , тобто , тобто 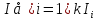 , то , то 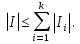 Розбиття проміжка і база в множині розбиттів. Нехай задано проміжок 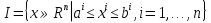 . Розбиття координатних відрізків . Розбиття координатних відрізків 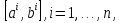 індукують розбиття проміжка І на більш менші проміжки, які отримуються прямим добутком проміжків розбиття вказаних координатних відрізків. індукують розбиття проміжка І на більш менші проміжки, які отримуються прямим добутком проміжків розбиття вказаних координатних відрізків.Означення 3. Описане задання проміжка I( у вигляді об’єднання 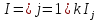 більш маленьких проміжків більш маленьких проміжків 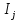 ) будемо називати розбиттям проміжка І і позначати символом Р. ) будемо називати розбиттям проміжка І і позначати символом Р. Означення 4. Величина 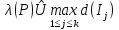 (максимальна з діаметрів проміжків розбиття Р) називається параметром розбиття Р. (максимальна з діаметрів проміжків розбиття Р) називається параметром розбиття Р.Означення 5. Якщо в кожному проміжку 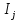 розбиття Р зафіксована деяка точка розбиття Р зафіксована деяка точка 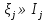 , то кажуть, що є розбиття з відміченими точками. , то кажуть, що є розбиття з відміченими точками.Набір 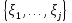 будемо позначати одним символом будемо позначати одним символом 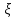 , а розбиття з відміченими точками – символом , а розбиття з відміченими точками – символом 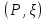 . .В множині 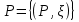 розбиттям з відміченими точками проміжка І вводиться база розбиттям з відміченими точками проміжка І вводиться база 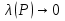 , елементи , елементи 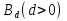 якої визначаються відношенням якої визначаються відношенням 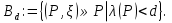 Те, що 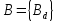 – дійсно база, випливає із існування розбиттів с параметром – дійсно база, випливає із існування розбиттів с параметром 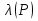 , як завгодно близьким до нуля. , як завгодно близьким до нуля.Інтегральна сума і інтеграл. Нехай f: I 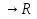 функція на проміжку І, а Р = функція на проміжку І, а Р = 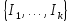 – розбиття цього проміжка з відміченими точками – розбиття цього проміжка з відміченими точками 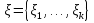 . .Означення 6. Сума 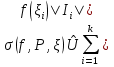 називається інтегральною сумою Рімана функції 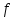 , яка відповідає розбиттю , яка відповідає розбиттю 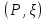 з відміченими точками проміжка І. з відміченими точками проміжка І.Означення 7. Величина 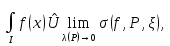 якщо вказана границя існує, називається інтегралом (Рімана) від функції 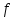 на проміжку І. на проміжку І.Ми бачимо, що дане визначення і взагалі увесь процес побудови інтеграла на проміжку 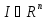 слово в слово повторює вже знайому нам процедуру визначення інтеграла Рімана на відрізку. Для більшої схожості ми навіть залишили колишній вид слово в слово повторює вже знайому нам процедуру визначення інтеграла Рімана на відрізку. Для більшої схожості ми навіть залишили колишній вид 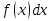 підінтегрального виразу. підінтегрального виразу. Рівносильні, але більш розгорнуті позначення інтеграла такі: 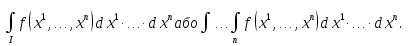 Щоб підкреслити, що мова йде про інтеграл на багатовимірній області І, кажуть, що це кратний інтеграл (подвійний, потрійний і т.д. у відповідністю з розмірністю І. Більш детальне визначення дав М.О. Давидов. Нехай функція u=f(x,y,z) визначена в замиканні кубовної відкритої множини G. Скінченну систему 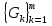 відкритих кубовних множин відкритих кубовних множин 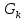 (k =1, 2, ..., m) (k =1, 2, ..., m) 1) 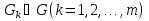 ; ;2) 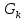 попарно без спільних точок; попарно без спільних точок;3) 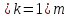 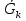 = = 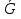 Тут натуральне число m може бути яким завгодно, але обов’язково скінченним. Прикладом (Т) – розбиття кубовної відкритої множини 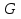 може бути сукупність всіляких перерізів даної множини може бути сукупність всіляких перерізів даної множини 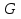 з відкритими паралелепіпедами з відкритими паралелепіпедами 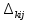 , які дістають при розбитті простору , які дістають при розбитті простору 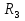 площинами, паралельними площинам координат. Якщо паралелепіпед площинами, паралельними площинам координат. Якщо паралелепіпед 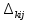 повність міститься в G, то повність міститься в G, то 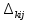 – відкрита кубовна множина. Якщо ж – відкрита кубовна множина. Якщо ж 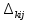 не повністю складається з точок множини G, але містить принаймні одну точку з G, то переріз не повністю складається з точок множини G, але містить принаймні одну точку з G, то переріз 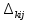 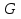 кубовний, оскільки межа цієї множини складається з частин межі прямокутного паралелепіпеда і частин межі множини G. Але межі цих двох множин мають міру нуль, тому частини їхніх меж також мають міру нуль і , отже, множина кубовний, оскільки межа цієї множини складається з частин межі прямокутного паралелепіпеда і частин межі множини G. Але межі цих двох множин мають міру нуль, тому частини їхніх меж також мають міру нуль і , отже, множина 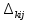 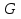 кубовна. Вона, будучи перерізом двох відкритих множин, є множиною відкритою. Сукупність всіляких непорожніх перерізів даної кубовної відкритої множини G з відкритими прямокутними паралелепіпедами кубовна. Вона, будучи перерізом двох відкритих множин, є множиною відкритою. Сукупність всіляких непорожніх перерізів даної кубовної відкритої множини G з відкритими прямокутними паралелепіпедами 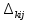 утворює (Т) – розбиття множини G. утворює (Т) – розбиття множини G.Візьмемо (Т) – розбиття множини G = 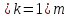 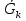 . В кожній множині . В кожній множині 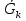 (k = 1, 2, . . . , m) візьмемо по одній точці (k = 1, 2, . . . , m) візьмемо по одній точці 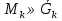 і складемо суму і складемо суму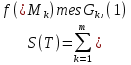 де mes 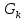 – об’єм кубовної відкритої множини – об’єм кубовної відкритої множини 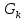 . Сума (1) називається потрійною інтегральною сумою Рімана, складеної для функції u = f(x,y,z), даного (Т)-розбиття . Сума (1) називається потрійною інтегральною сумою Рімана, складеної для функції u = f(x,y,z), даного (Т)-розбиття 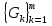 множини G і даного вибору точок множини G і даного вибору точок 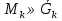 (k = 1, 2, . . . , m). (k = 1, 2, . . . , m). Позначаючи через 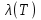 = = 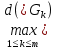 , де , де 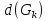 – діаметр множини – діаметр множини 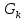 . .Число І називається границею інтегральних сум (1) при 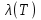 → 0, якщо для будь-якого числа → 0, якщо для будь-якого числа 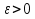 існує число існує число 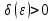 таке, що таке, що| 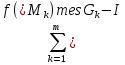 | < | < 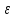 для будь-якого (Т) – розбиття 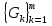 множини G і будь-якого вибору точок множини G і будь-якого вибору точок 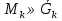 (k = 1, 2, . . . , m), для якого (k = 1, 2, . . . , m), для якого 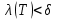 . .Якщо при 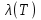 → 0 інтегральні суми (1) мають границю I, то її називають потрійним інтегралом Рімана від функції f(x,y,z) по кубовній множині G (або по → 0 інтегральні суми (1) мають границю I, то її називають потрійним інтегралом Рімана від функції f(x,y,z) по кубовній множині G (або по 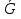 ) і позначають ) і позначають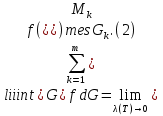 У цих позначеннях замість G пишуть також множину 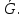 Множину G (а також Множину G (а також 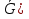 називають областю інтегрування. називають областю інтегрування.Якщо границя (2) існує, тобто якщо існує потрійний інтеграл від функції f(x,y,z) по кубовній відкритій множині G, то функція f(x,y,z) називається інтегровною за Ріманом на множині G ( на множині 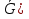 . . Лема. Нехай G – відкрита квадровна ( кубовна) множина, 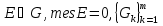 — (T)-розбиття множини G. Якщо — (T)-розбиття множини G. Якщо 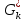 —множини —множини 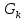 , замикання яких перерізають з E, то , замикання яких перерізають з E, то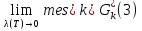 Доведення. Задамо число 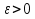 , тоді для числа , тоді для числа 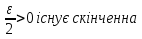 Система замкнених прямокутників 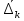 (замкнених прямокутних паралелепіпедів (замкнених прямокутних паралелепіпедів 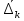 ) (k = 1, 2, …, p), які покривають множину Е, і така, що ) (k = 1, 2, …, p), які покривають множину Е, і така, що 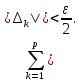 Позначимо 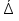 = = 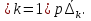 На межі площини На межі площини 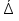 можуть бути точки множини Е. Кожний прямокутник можуть бути точки множини Е. Кожний прямокутник 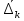 ( прямокутний паралелепіпед) візьмемо всередину прямокутника ( прямокутний паралелепіпед) візьмемо всередину прямокутника 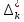 (прямокутного паралелепіпеда), причому (прямокутного паралелепіпеда), причому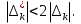 Розглянемо замкнену множину 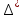 , яка складається із скінченного числа замкнених прямокутників , яка складається із скінченного числа замкнених прямокутників 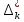 ( прямокутних паралелепіпедів), що містить у собі множину ( прямокутних паралелепіпедів), що містить у собі множину 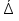 , і таку, що , і таку, що 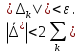 Межа множини 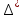 не містить точок площини Е, ні граничних точок цієї множини. Тоді, позначивши межі множин не містить точок площини Е, ні граничних точок цієї множини. Тоді, позначивши межі множин 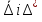 відповідно через G i відповідно через G i 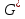 , маємо , маємо 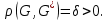 Якщо Якщо 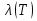 < < 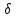 , то множини , то множини 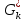 повністю помістяться в повністю помістяться в 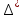 , і ,отже, , і ,отже, 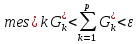 Цим рівність (3) доведено. Теорема 1. Нехай G – відкрита квадровна (кубовна) множина, E 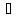 іG, mesE = 0 і іG, mesE = 0 і 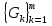 - (T)-розбиття множини G. Якщо - (T)-розбиття множини G. Якщо 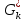 - множини - множини 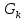 , замикання яких перерізаються з E, f – функція, визначена і обмежена на , замикання яких перерізаються з E, f – функція, визначена і обмежена на 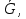 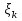 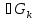 (k = 1, 2, …, m), (k = 1, 2, …, m),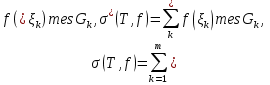 де в другій сумі підсумовування відбувається по всіх k, для яких 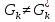 , то границя , то границя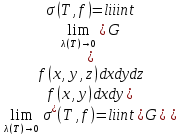 існує тоді і тільки тоді, коли існує границя існує тоді і тільки тоді, коли існує границя 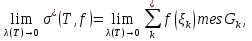 причому якщо остання границя існує, то вона також дорівнює 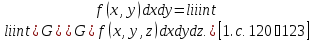 При побудові загального поняття потрійного інтеграла у Г.М.Фіхтенгольца основну роль відіграє поняття об’єму тіла, так як поняття площі лежало в основі поняття подвійного інтеграла. З поняттям об’єму ми вже знайомі. Умовою існування об’єму для даного тіла полягає в тому, щоб поверхня, яка його обмежує мала об’єм рівний нулю. Варто відмітити, що до таких поверхонь відносять гладкі та кусково-гладкі поверхні. Нехай тепер в деякій просторовій області (V) задана функція f(x,y,z). Розіб’ємо цю область на скінченну кількість частин (V1),(V2),…,(Vn), які мають відповідні об’єми V1, V2,…,Vn. В межах і-го елемента (Vi) візьмемо довільну точку 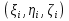 , значення функції в цій точці , значення функції в цій точці 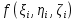 помножимо на об’єм Viі складемо інтегральну суму помножимо на об’єм Viі складемо інтегральну суму 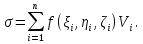 Границя І цієї суми, при прямуванні до нуля найбільшого із діаметрів всіх областей (Vi), і називається потрійним інтегралом функції f(x,y,z) в області (V).Він позначається символом 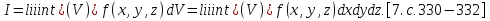 |
