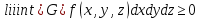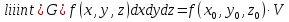КондратьєваПотрійні. геометричні та механічні застосування потрійного інтеграла
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
|
Властивості та умова існування потрійних інтегралів Умова існування потрійного інтеграла. Теорема (достатня умова). Якщо функція f( x, y, z) неперервна в обмеженій замкненій області G, то вона в цій області інтегрована. Властивості потрійного інтеграла.
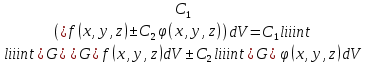
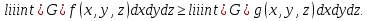
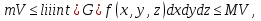 де m і M – відповідно найменше і найбільше значення функції f(x, y, z) в області G.
Величина 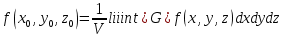 називається середнім значенням функції f(x, y, z) в області G. називається середнім значенням функції f(x, y, z) в області G.
Якщо область інтегрування G така, що її проекція на площину Oxy , область D , правильна в напрямку осі Oy , а всяка пряма, що проходить через внутрішню точку області D паралельно осі Oz перетинає границю області G рівно в двох точках (точка входу N та точка виходу K ), які лежать на поверхнях z=z1(x, y), z=z2(x, y), то: 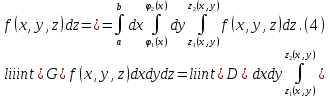 У цій формулі спочатку обчислюється інтеграл по змінній z при умові, що x, y – сталі величини, після чого отримують подвійний інтеграл по змінних y і x. Варто відмітити, що область D, яка задовольняє вказаним вище умовам, називається правильною у напрямі осі Oz. Якщо область D правильна у напрямі осі Ox, то формула (4) запишеться по-іншому 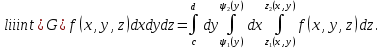 Мал. 1.1 Якщо ж, наприклад, область G правильна у напрямі осі Ox: 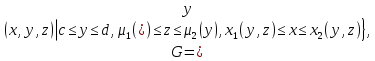 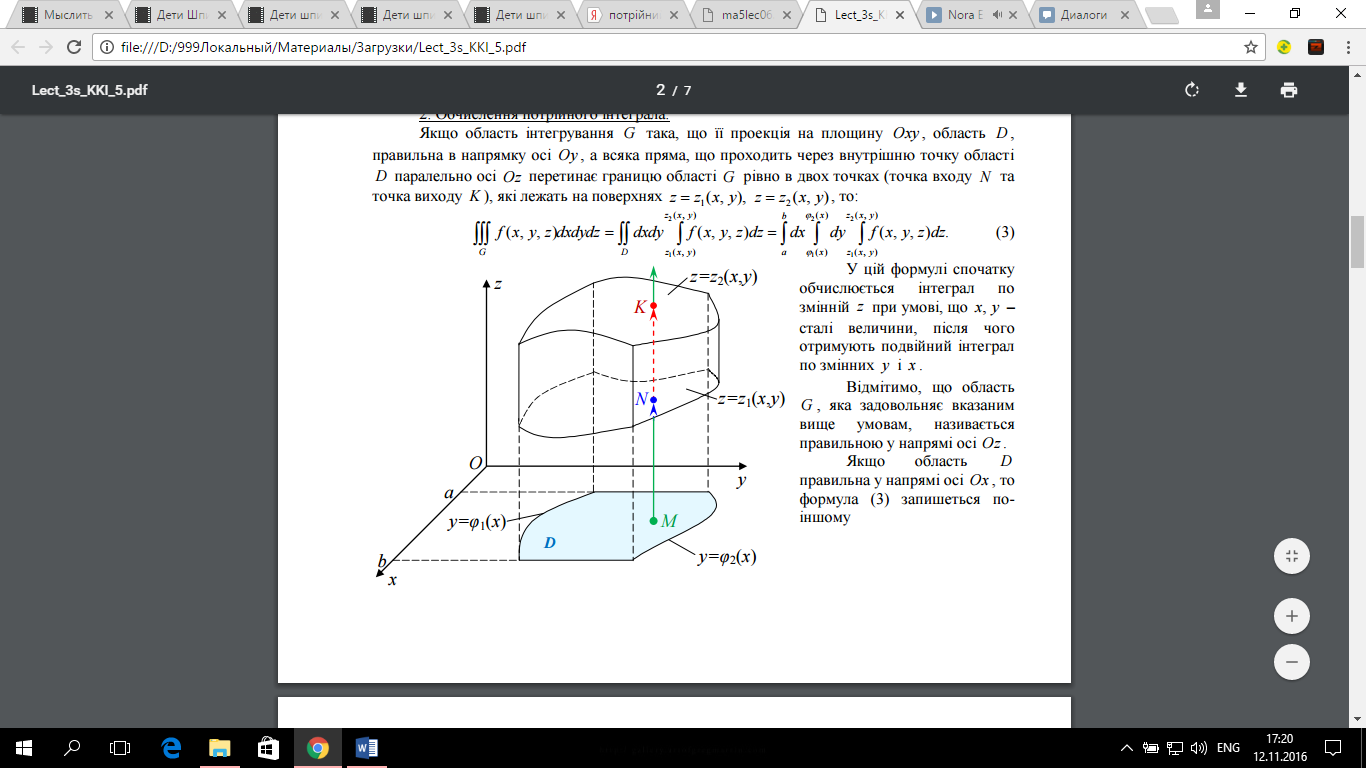 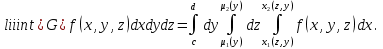 У випадку, якщо область G правильна у всіх напрямах, то повторний інтеграл можна записати 6-ма різними способами. Порядок інтегрування потрібно обирати так, щоб обчислення були найпростішими.
В циліндричній системі координат положення точки M(x, y, z) 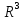 однозначно визначається числами , , z , де z — апліката точки M , а , , — полярні координати проекції M точки M на площину Oxy. Числа , і z називають циліндричними координатами точки M. однозначно визначається числами , , z , де z — апліката точки M , а , , — полярні координати проекції M точки M на площину Oxy. Числа , і z називають циліндричними координатами точки M.Мал. 1.2 Якщо полярна вісь співпадає з додатним напрямом осі Ox , а полюс O з початком координат, то циліндричні координати зв’язані з декартовими за формулами  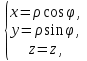 Де 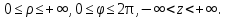 Знайдемо якобіан відображення 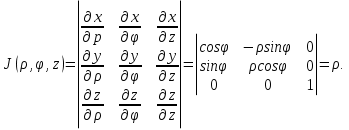 Оскільки 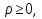 то то 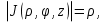 то тоді формула переходу від потрійного інтеграла в прямокутних координатах до інтеграла в циліндричних координатах має вигляд то тоді формула переходу від потрійного інтеграла в прямокутних координатах до інтеграла в циліндричних координатах має вигляд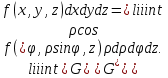 Вираз 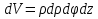 називають елементом об’єму в циліндричних координатах. називають елементом об’єму в циліндричних координатах.Мал. 1.3 В сферичній системі координат положення точки M( x; y; z) R3 визначається трьома числами r, , , де r — відстань від точки M до початку координат, — кут між віссю Ox і проекцією радіус-вектора 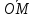 точки M на площину Oxy , а — кут між віссю Oz і радіус-вектором точки M на площину Oxy , а — кут між віссю Oz і радіус-вектором 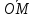 точки M , що відраховується від осі Oz. точки M , що відраховується від осі Oz.  Числа r, і називають сферичними координатами точки M. Перехід від декартових координат до сферичних здійснюється за формулами 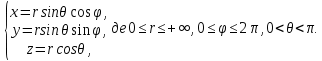 Координатними поверхнями в сферичній системі координат є: сфери r=const з центром в початку координат, 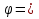 const — півплощини, що проходять через вісь Oz і кругові конуси const — півплощини, що проходять через вісь Oz і кругові конуси 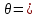 const з віссю Oz. const з віссю Oz. Визначимо якобіан аналогічно до випадку циліндричних координат. Маємо 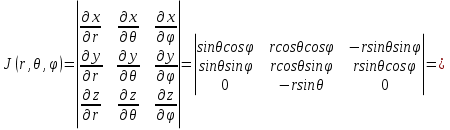 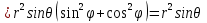 Враховуючи, що 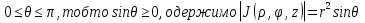 Тоді формула переходу до сферичних координат має вигляд 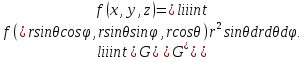 Вираз 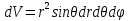 називають елементом об’єму в сферичних координатах. називають елементом об’єму в сферичних координатах.
Формула Остроградського — формула, що виражає потік векторного поля через замкнену поверхню через інтеграл від дивергенції цього поля по об'єму, замкнутий під поверхнею та пов’язує потрійний інтеграл на просторі з поверхневим інтегралом на контурі області. Розглянемо тіло (V) обмежене гладкими поверхнями 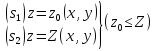 і циліндричною поверхнею 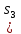 ), яка паралельна осі Оz. ), яка паралельна осі Оz. Напрямною тут буде кусково-гладка замкнена крива (К) з нульової площею на площині Oxy, яка обмежена областю (D) – проекцією тіла (V)на цю площину. Припустимо, що в області (V) визначена деяка функція R(x, y, z), неперервна разом зі своєю похідною 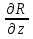 на всій області (V), включаючи контур. Тоді має місце формула: на всій області (V), включаючи контур. Тоді має місце формула: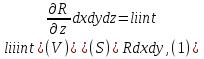 причому 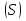 є поверхнею, яка обмежує тіло, і інтеграл праворуч розповсюджений на зовнішню її сторону. є поверхнею, яка обмежує тіло, і інтеграл праворуч розповсюджений на зовнішню її сторону.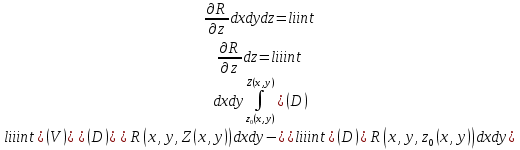 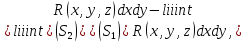 причому перший з інтегралів праворуч розповсюджений на верхню сторону поверхні ( 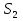 ), а другий – на нижню сторону поверхні ( ), а другий – на нижню сторону поверхні (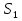 ). Рівність не зміниться, якщо ми допишемо інтеграл ). Рівність не зміниться, якщо ми допишемо інтеграл 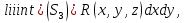 який розповсюджений на зовнішню сторону поверхні 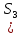 ), так як цей інтеграл дорівнює нулю. Об’єднуючи всі три поверхневі інтеграли маємо формулу (1), яка є частинним випадком формули Остроградського. ), так як цей інтеграл дорівнює нулю. Об’єднуючи всі три поверхневі інтеграли маємо формулу (1), яка є частинним випадком формули Остроградського. Аналогічно формулі (1) мають місце формули: 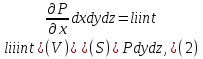 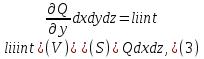 якщо функції 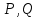 неперервні на області неперервні на області 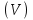 разом зі своїми похідними разом зі своїми похідними 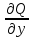 , ,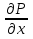 . .Склавши всі три формули (1), (2), (3) ми виведемо формулу Остроградського. 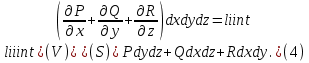 Ця формула виражає поверхневий інтеграл другого типу в загальному вигляді, який розповсюджений на зовнішню сторону замкненої поверхні, через потрійний інтеграл, який взято по тілу, яке обмежене цією поверхнею. Зауваження. Іноді формулу Остроградського пов’язують з ім’ям Гаусса. У Гаусса зустрічаються лише дуже частинні випадки цієї формули, до того ж кожного разу по-новому дається їх виведення. В загальному вигляді (4) ця формула вперше була представлена у 1828 році Остроградським, який застосував її до проблеми розповсюдження тепла в твердому тілі. Отже, формула Остроградського має одну ідею: вона виражає інтеграл, розповсюджений на деякому геометричному образі, через інтеграл, який взято на контурі цього образу. РОЗДІЛ II. Практичне застосування 2.1 Механічні застосування потрійного інтеграла Маса. Нехай маса розподілена в кубовній замкненій області 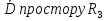 з об’ємною густиною в точці (x, y, z) з об’ємною густиною в точці (x, y, z) 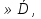 що дорівнює що дорівнює 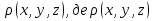 – неперервна функція в замкненій області – неперервна функція в замкненій області 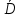 . Ця маса утворює неоднорідне матеріальне тіло. Знаючи об’ємну густину . Ця маса утворює неоднорідне матеріальне тіло. Знаючи об’ємну густину 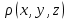 маси в кожній точці маси в кожній точці(x, y, z) 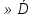 , обчислимо масу матеріального тіла. , обчислимо масу матеріального тіла.Тут розглянемо (T)-розбиття області 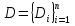 . У замиканні кожної області . У замиканні кожної області 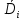 беремо по дві точки беремо по дві точки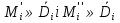 такі, що такі, що 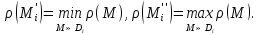 Тоді 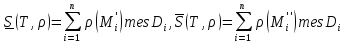 даватимуть наближені значення маси тіла, причому перша сума дає наближене значення з недостачею, а друга – з надлишком. Якщо найбільший діаметр областей 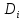 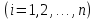 позначити через позначити через 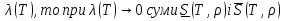 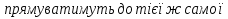 границі, яка дорівнює потрійному інтегралу: границі, яка дорівнює потрійному інтегралу: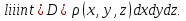 Отже, маса m матеріального тіла з об’ємною щільністю маси в точці (x, y, z) 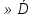 , що дорівнює , що дорівнює 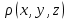 , обчислюється за формулою , обчислюється за формулою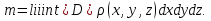 Зокрема, якщо тіло однорідне і об’ємна густина маси дорівнює одиниці, то маса тіла дорівнює його об’єму V, тобто 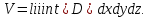 Також можна дістати формули для координат центра маси, розподіленої по кубовній замкненій області 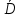 з об’ємною густиною в точці (x, y, z) з об’ємною густиною в точці (x, y, z) 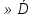 , яка дорівнює , яка дорівнює 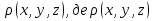 - неперервна функція у замкненій області - неперервна функція у замкненій області 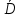 . . 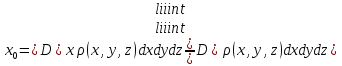 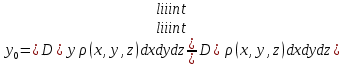 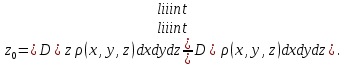 Приклад 9. Обчислити масу m тіла, обмеженого площинами x=0, y=0, z=0, x + y+ z=2, x=1, y=1, якщо його густина дорівнює 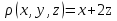  Розв’язування. Мал. 2.7 Проекцією тіла на координатну площину Oxy є фігура ОАВС, утворена прямими х=0, y=0, x=1, y=1. Зрозуміло, змінні х та у змінюються в межах від 0 до 1. При фіксованих х, у точка може рухатися по вертикалі від площини z=0 до площини x+y+z=2; таким чином апліката z буде змінюватися в межах від 0 і до 2-x-y. Тоді: 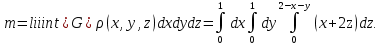 Послідовно обчислюючи інтеграли, одержимо: 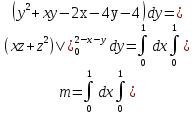 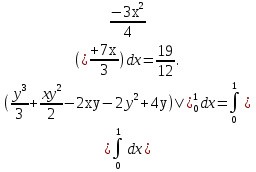 Відповідь: 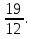 Центр маси тіла Для обчислення координат центра маси тіла потрібні статистичні моменти відносно координатних площин Оху, Охz, Оуz; позначимо їх відповідно 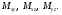 Отримаємо наступні формули для координат Отримаємо наступні формули для координат 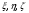 центра маси неоднорідного тіла, густина якого задається функцією центра маси неоднорідного тіла, густина якого задається функцією 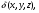 яка займає область яка займає область 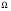 : :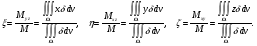 Якщо тіло однорідне, тобто 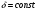 , то формули спрощуються: , то формули спрощуються: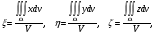 де V- об’єм тіла. Приклад 10. Знайдемо центр маси однорідної півкулі 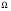 : : 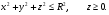 Дві координати центра маси 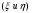 дорівнюють нулю, бо півкуля симетрична відносно осі Оz (тіло обертання з віссю Оz). дорівнюють нулю, бо півкуля симетрична відносно осі Оz (тіло обертання з віссю Оz).Інтеграл 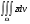 зручно обчислювати, перейшовши до сферичних координат: зручно обчислювати, перейшовши до сферичних координат: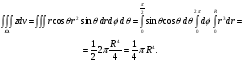 Так як об’єм сфери дорівнює 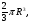 то то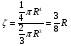 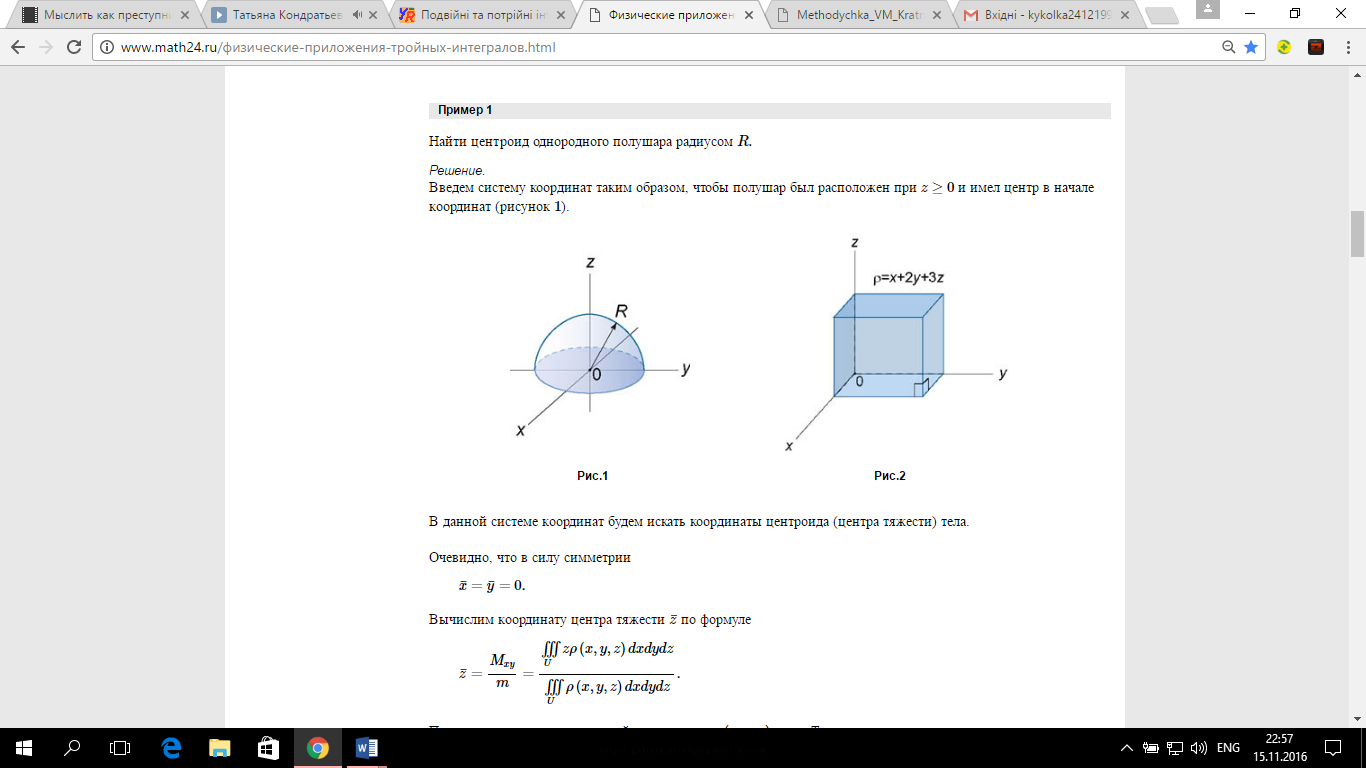 Приклад 11. Визначити масу і координати центра маси одиничного куба з щільністю 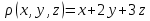 . . Розв’язування. Мал. 2.8 Спочатку обчислимо масу куба: 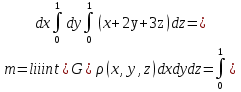 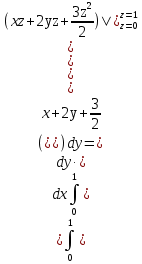 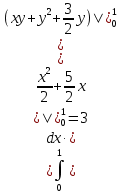 Тепер обчислимо статистичні моменти 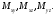 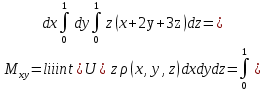 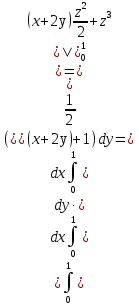 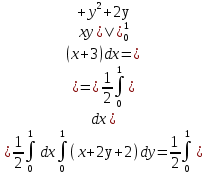 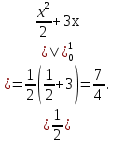 Аналогічно знаходимо Myz и Myx: 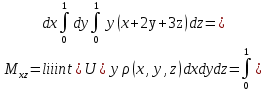 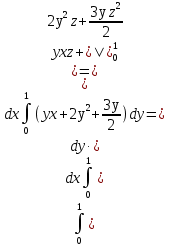 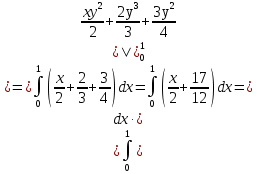 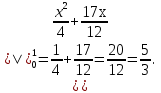 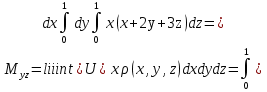 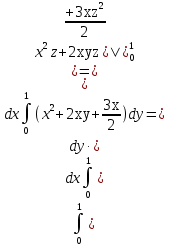 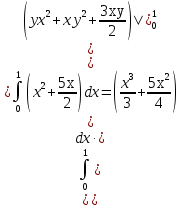 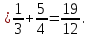 Обчислюємо координати центра ваги куба: 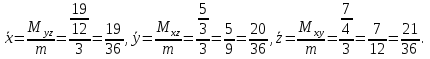 Відповідь: 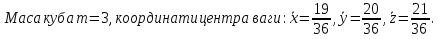 Момент інерції Поняття моменту інерції тіла належить до основних і важливих понять у динаміці. Його ввів Л. Ейлер. Перейдемо до обчислення моментів інерції відносно координатних осей. Так як квадрати відстаней від точки P(x, y, z) до осей Ox, Oy, Oz відповідно дорівнюють 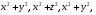 то нехай для спрощення то нехай для спрощення 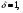 отримаємо наступні формули : отримаємо наступні формули :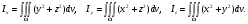 Аналогічно випадку для площин інтеграли 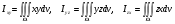 називаються відцентровимимоментами інерції. Для полярного момента інерції формула має вигляд 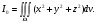 Якщо тіло не однорідне, то в кожній формулі під знаком інтеграла буде знаходитись додатковий множник 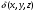 - густина тіла в точці P. - густина тіла в точці P.Приклад 12. Обчислимо полярний момент інерції однорідної кулі, радіуса R. У цьому випадку буде зручно перейти до сферичних координат. Матимемо 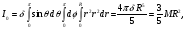 де М—маса кулі. Так як для сфери момент інерції відносно осей координат, вочевидь, рівні між собою, то, враховуючи, що 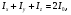 отримаємо отримаємо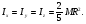 Моменти інерції відносно осі відіграють важливу роль при обчисленні кінетичної енергії тіла при його обертанні навколо відповідної осі. Нехай тіло 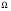 обертається навколо осі Оz з постійною кутовою швидкістю обертається навколо осі Оz з постійною кутовою швидкістю 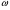 . Знайдемо кінетичну енергію тіла . Знайдемо кінетичну енергію тіла 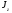 . Як відомо, кінетична енергія точки вимірюється величиною . Як відомо, кінетична енергія точки вимірюється величиною 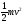 , где т - маса точки, а , где т - маса точки, а  - величина її швидкості. Кінетична енергія системи точок визначається як сума кінетичних енергій окремих точок, а кінетична енергія тіла – як сума кінетичних енергій всіх частин , на які воно було розбите. Ця обставина дозволяє застосовувати для обчислення кінетичної енергії інтеграл. - величина її швидкості. Кінетична енергія системи точок визначається як сума кінетичних енергій окремих точок, а кінетична енергія тіла – як сума кінетичних енергій всіх частин , на які воно було розбите. Ця обставина дозволяє застосовувати для обчислення кінетичної енергії інтеграл.Візьмемо який-небудь окіл 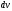 точки Р(х, у, z) тіла точки Р(х, у, z) тіла 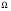 . Величина лінійної швидкості . Величина лінійної швидкості  точки Р при обертанні навколо осі Оz дорівнює точки Р при обертанні навколо осі Оz дорівнює 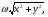 а отже, кінетична енергія частини а отже, кінетична енергія частини 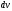 тіла тіла 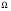 можна виразити так : можна виразити так :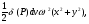 де 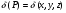 - густина тіла в точці Р. Для кінетичної енергії усього тіла - густина тіла в точці Р. Для кінетичної енергії усього тіла 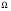 маємо маємо 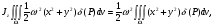 тобто 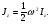 Кінетична енергія тіла, яке обертається навколо деякої осі з постійною кутовою швидкістю, дорівнює половині квадрата кутової швидкості, помноженої на момент інерції тіла відносно осі обертання. Приклад 5. Знайти момент інерції прямого кругового конуса відносно його осі. Конус має радіус основи R, висотуH і загальну масу m (Мал. 2.3). Розв’язування. Момент інерції тіла відносно осі Oz виражається за формулою 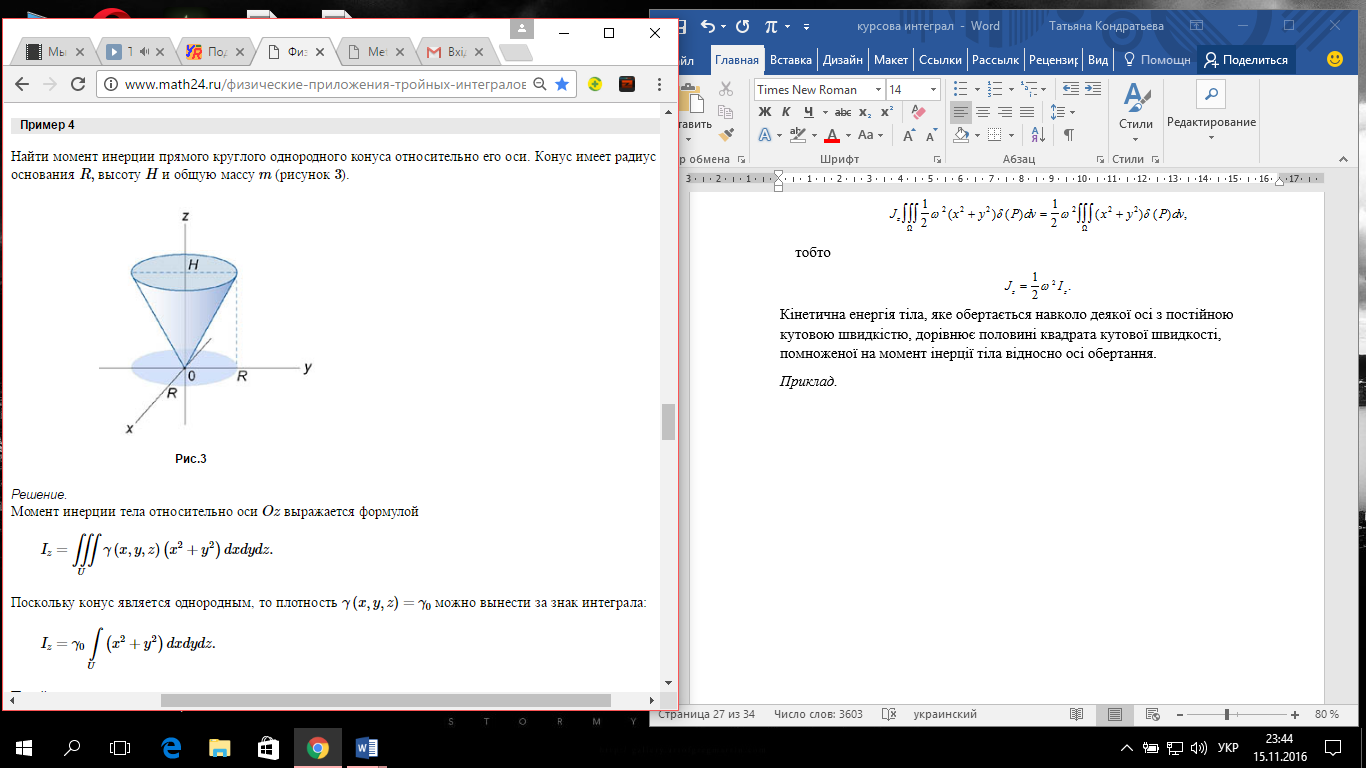 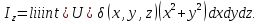 Мал. 2.3 Оскільки конус є однорідним, то 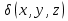 = = 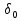 можна винести за знак інтеграла: можна винести за знак інтеграла: 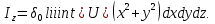 Перейдемо до циліндричних координат за допомогою заміни 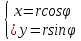 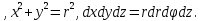 Тоді : 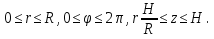 Тоді момент інерції дорівнює: 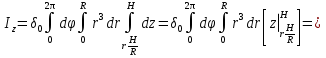 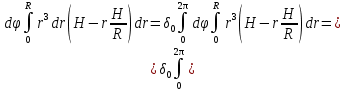 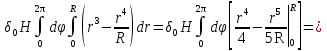 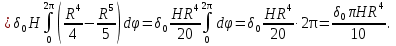 Виразимо густину 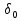 через відому масу конуса m. Так як через відому масу конуса m. Так як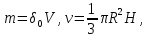 тоді: 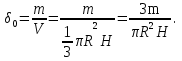 Отже, 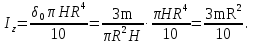 Варто зауважити, що момент інерції не залежить від висоти конуса. Відповідь: 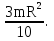 |