Гидравлика и нефтегазовая гидромеханика
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Уфимский государственный нефтяной технический университет» Кафедра «Гидрогазодинамика трубопроводных систем и гидромашины» Курсовая работа «Гидравлический расчет сложного трубопровода и элементов оборудования» по дисциплине «Гидравлика и нефтегазовая гидромеханика» Выполнил: студент гр. БГГ-17-01 О.А. Прокопьев Проверил: доцент И.М. Руфанова Уфа 2019 СОДЕРЖАНИЕ 1. Решение задач………………………………………. …...……………………………4 2. Гидравлический расчет разветвленного трубопровода………………………….....10 Список использованных источников …………………………………………………..20 1. Решение задач Задача 1.34 К отверстию в дне открытого резервуара А, частично заполненного водой, присоединена вертикальная труба, нижним концом опущенная под уровень воды в резервуаре В. При закрытой задвижке труба заполнена водой; расстояние между уровнями воды в резервуарах Н = 2 м; избыточное давление воздуха в резервуаре Р = 60кПа; толщина воздушной подушки h = 0,5 м. Атмосферное давление Рат = 100 кПа. Определить, какой объем воды переместится из одного резервуара в другой после открытия задвижки в трубе. Процесс расширения воздуха в резервуаре В считать изотермическим. Диаметры резервуаров одинаковы: D = 1 м, диаметр трубы d = 0,2 м.  Рисунок 1.1  Решение: Абсолютное давление в резервуаре В при закрытой задвижке:  При этом давлении объем воздуха в сосуде В:  Высота в трубе до задвижки: 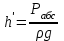 При открытой задвижке избыточное давление в резервуаре В: 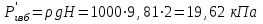 Так как 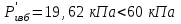 , то воздух будет расширяться. Пусть , то воздух будет расширяться. Пусть 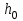 – понижение уровня в сосуде B, то понижение уровня – понижение уровня в сосуде B, то понижение уровня  в сосуде А определяется из условия сохранения объема: в сосуде А определяется из условия сохранения объема: 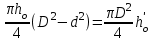  Абсолютное давление воздуха при открытой задвижке: 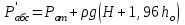 Так как процесс изотермический, то справедливо применить закон Бойля-Мариотта:  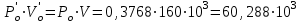   Преобразуя данное уравнение, приходим к квадратному:  , ,откуда  Тогда объем воды, который переместится из одного резервуара в другой после открытия задвижки в трубе, равен: 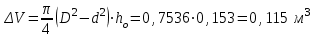 Ответ: после открытия задвижки в трубе из одного резервуара в другой переместится объем  воды. воды.Задача 2.5 Щитовой затвор должен автоматически опрокидываться для пропуска воды при уровне последней H1 ≥ 6 м. Щит поворачивается на цапфах О диаметром d = 0,4 м, имеющих коэффициент трения скольжения f = 0,2. Ширина щита B = 8 м, его угол наклона α = 600. Найти, на каком расстоянии x должна быть расположена ось поворота щита, если под ним имеется постоянный уровень воды H2 = 3 м, и определить силу P, воспринимаемую его опорами в момент опрокидывания. 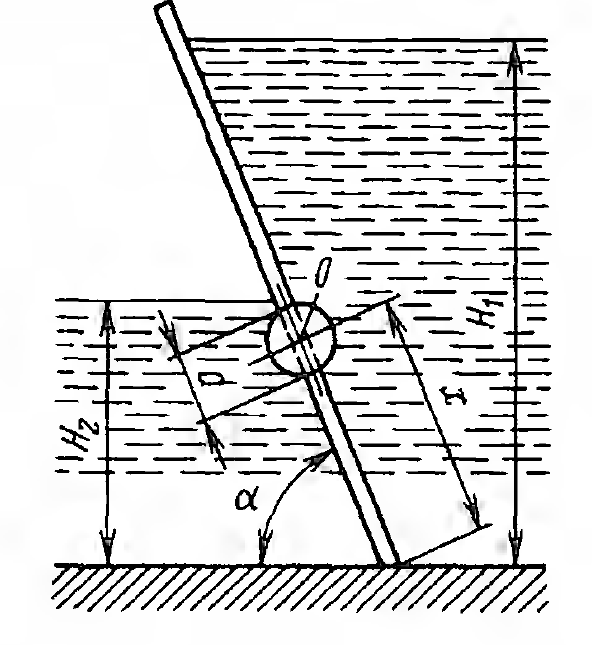 Рисунок 1.2 Решение: 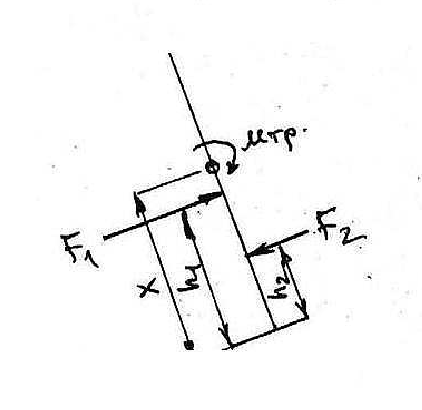 Сила давления на затвор справа и слева:   Расстояние от плоскости уровня жидкости до точек приложения этих сил:   Тогда расстояние от дна до точек приложения этих сил: 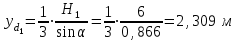  Сила, воспринимаемая опорами в момент опрокидывания:  Момент трения в опорах: 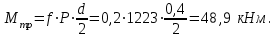 Из условия равновесия щита: 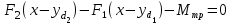 Определим x:  . .Ответ: на расстоянии 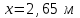 должна быть расположена ось поворота щита, а сила, воспринимаемая его опорами в момент опрокидывания равна должна быть расположена ось поворота щита, а сила, воспринимаемая его опорами в момент опрокидывания равна  . . 2. Гидравлический расчет разветвленного трубопровода 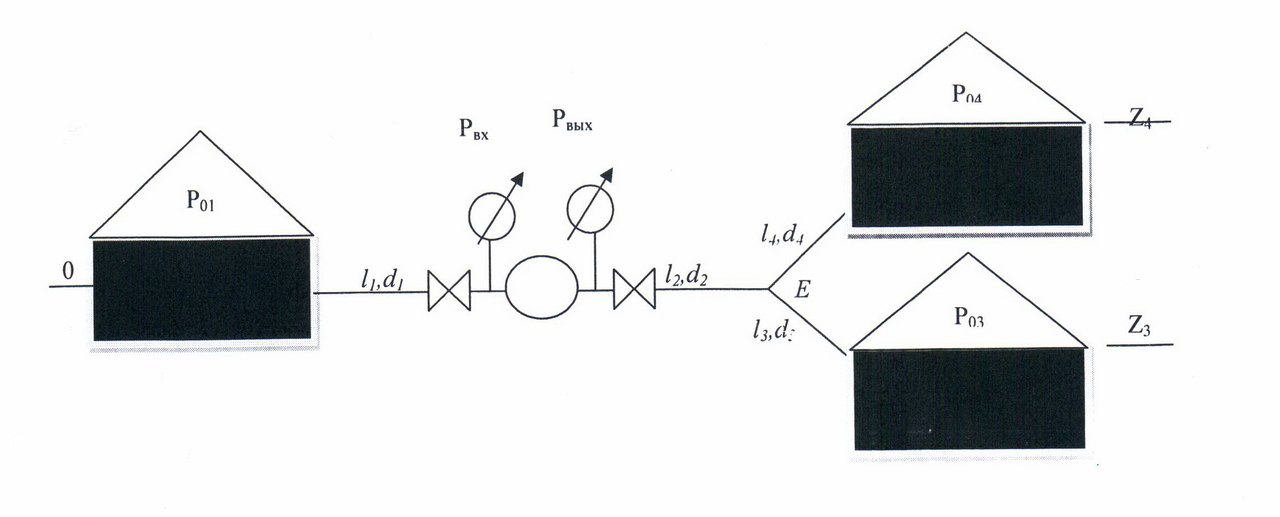 Исходные данные: Проектный расход, Q1=Q2=300 м3/час Перекачиваемая жидкость,  = 850 кг/м3; = 850 кг/м3;  м2/c м2/c Эквивалентная шероховатость труб K=0,05 мм
Из рисунка видно, что Q=Q1=Q2=Q3+Q4 2.1.1. Составим уравнение Бернулли для входного сечения (1-вх): 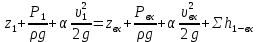 , ,где  - высотная отметка начального сечения; - высотная отметка начального сечения; – избыточное давление на свободной поверхности в первом резервуаре; – избыточное давление на свободной поверхности в первом резервуаре; –высотная отметка входа в насос; –высотная отметка входа в насос;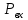 –избыточное давление на входе в насос; –избыточное давление на входе в насос;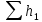 – суммарные потери напора в первом трубопроводе – суммарные потери напора в первом трубопроводе = = 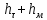 = = 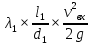 + +  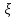 , где , где 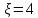 (сопротивление на вентиле), (сопротивление на вентиле),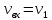 = const; = const;  = = 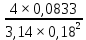 = 3,27 м/с; = 3,27 м/с;Найдем число Рейнольдса: Re =  = = 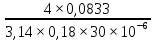 = 19650; = 19650;Определим переходные числа Рейнольдса:  = =  = = 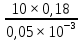 = 36000, где К- эквивалентная шероховатость труб. = 36000, где К- эквивалентная шероховатость труб. = =  = =  = 1800000; = 1800000;Так как  , то режим движения турбулентный, зона гидравлически гладких труб, и λ определяем по формуле Блазиуса: , то режим движения турбулентный, зона гидравлически гладких труб, и λ определяем по формуле Блазиуса: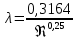 = =  = 0,0267; = 0,0267;Найдем потери напора:  = 0,0267 = 0,0267 + + 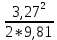  =10,264 м; =10,264 м;Давление на входе:  = [2 + = [2 + 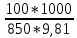 - 0 - 10,264] - 0 - 10,264] 850 850 9,81= = 31090,636 Па = 31,091 кПа 9,81= = 31090,636 Па = 31,091 кПа2.1.2. Запишем уравнение Бернулли для сечений (вых- E):  ; ;Так как zвых=0, zE=0,  , то формула примет вид: , то формула примет вид: ; ; [ [ ] ] ρg; ρg; = = 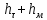 = =  + + 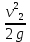  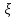 ; ;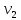 = =  = =  = 4,72 м/с; = 4,72 м/с;Найдем число Рейнольдса: Re =  = = 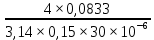 =23581; =23581;Определим переходные числа Рейнольдса:  = =  = =  = 30000; = 30000; = =  = =  = 1500000; = 1500000;Так как  , то режим движения турбулентный, зона гидравлически гладких труб, и λ определяем по формуле Блазиуса: , то режим движения турбулентный, зона гидравлически гладких труб, и λ определяем по формуле Блазиуса: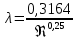 = =  = 0,0255; = 0,0255;Найдем потери напора:  = 0,0255 = 0,0255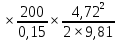 + + 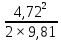  = 43,149 м; = 43,149 м; [ [ ] ] 850 850 9,81= 290202,064 Па =290,202 кПа. 9,81= 290202,064 Па =290,202 кПа.2.1.3. Запишем уравнение Бернулли для сечения (E-3): 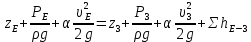 ; ;Определим потери напора: 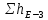 = =  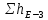 = =  = 20 м; = 20 м;Запишем уравнение Бернулли для сечения (E-4):  ; ;Определим потери напора: 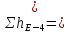  ; ; = = 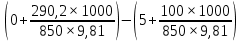 = 18 м; = 18 м;Рассчитаем гидравлические характеристики каждой из труб. Таблица 2.1. Данные для построения гидравлической характеристики трубопровода 3.
Таблица 2.1. Данные для построения гидравлической характеристики трубопровода 4.
Построим зависимость потерь напора от диаметра h=f(d), зная значения потерь для трубопровода 3 (  и для трубопровода 4 ( и для трубопровода 4 ( и определим диаметры трубопроводов. и определим диаметры трубопроводов.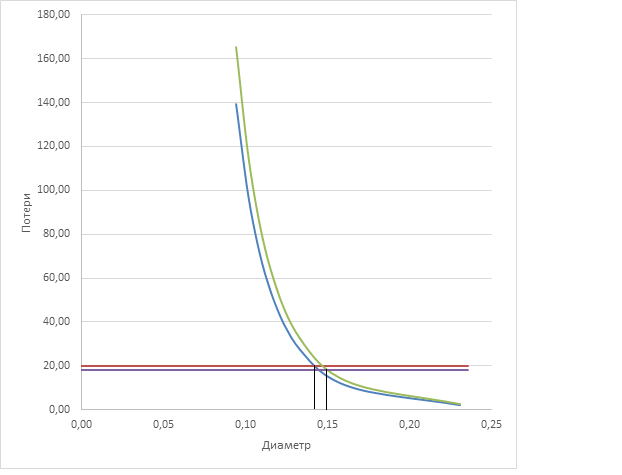 Рисунок 2.1 График зависимости потерь напора от диаметра для третьего и четвертого трубопроводов По графику найдем значения  и и  : :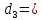 0,14 м = 140 мм; 0,14 м = 140 мм;  0,15 м = 150 мм; 0,15 м = 150 мм;2.2. Из рисунка видно, что Q1=Q2=Q3 Рассчитаем гидравлические характеристики каждой из труб. Таблица 2.2. Данные для построения гидравлической характеристики трубопровода 2.
Таблица 2.2. Данные для построения гидравлической характеристики трубопровода 3.
Построим график зависимости расхода от напора и определим расходы второго, третьего и четвертого трубопроводов.  Рисунок 2.2. График зависимости напора от расхода. В результате мы получили следующее значения расхода: Q= Q1=Q2=Q3 = 0,06 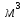 /с = 216 /с = 216 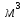 /ч /ч2.3. Проверим зависимость Q2,Q3, Q4 от 𝝂, построив гидравлические характеристики труб, по которым течет жидкость вязкость которой увеличим в 2,5 раза (𝝂2=2,5𝝂1=30 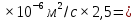 75 75 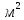 /с). Будем считать, что давление на выходе из насоса осталось прежним. Запишем систему уравнений: /с). Будем считать, что давление на выходе из насоса осталось прежним. Запишем систему уравнений: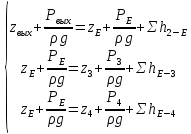 Введем обозначения: 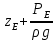 = =  ; ;  = =  ; ; 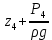 = = 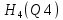 ; ;  и получим: и получим: где 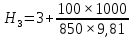 = 15 м; = 15 м;  = 5+ = 5+ 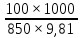 = 17 м. = 17 м.Рассчитаем гидравлические характеристики каждой из труб. Таблица 2.3. Данные для построения гидравлической характеристики трубопровода 2.
Таблица 2.3. Данные для построения гидравлической характеристики трубопровода 3.
Таблица 2.3. Данные для построения гидравлической характеристики трубопровода 4.
 Рисунок 2.3. Гидравлические характеристики трубопроводов, по которым течет жидкость вязкостью 𝝂=75*  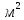 /с. /с.По графику видно, что при данной вязкости значения расходов будут равны: Q= Q1=Q2 = 0,073 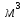 /с = 262,8 /с = 262,8 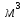 /ч /чQ3 =Q4 =  = 0,0365 = 0,0365 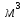 /с = 131,4 /с = 131,4 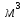 /ч /чСоответственно, с увеличением вязкости расход жидкости уменьшается. Вывод: в ходе выполнения гидравлического расчета разветвленного трубопровода было определено 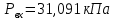 и диаметры третьего и четвертого трубопроводов и диаметры третьего и четвертого трубопроводов 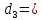 0,14 м, 0,14 м,  0,15 м; Определены расходы по всем ветвям, если отключить трубопровод №4: Q=Q1=Q2=Q3 = 216 0,15 м; Определены расходы по всем ветвям, если отключить трубопровод №4: Q=Q1=Q2=Q3 = 216 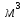 /ч; Доказано, что при увеличении вязкости (в 2,5 раза) расход уменьшается (в 2 раза): Q = Q1 = Q2 = 262,8 /ч; Доказано, что при увеличении вязкости (в 2,5 раза) расход уменьшается (в 2 раза): Q = Q1 = Q2 = 262,8 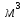 /ч; Q3 =Q4 = /ч; Q3 =Q4 =  = 131,4 = 131,4 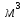 /ч /чСПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Сборник задач по машиностроительной гидравлике: Учеб. пособие для машиностроительных вузов / Д.А. Бутаев, З.А. Калмыкова, Л.Г. Подвизда и др.; Под ред. И.И. Куколевского, Л.Г. Подвизда. – 5-е изд., стереотипное. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. – 448с., ил. Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов / Т.М. Башта, С.С. Руднев, Б.Б. Некрасов и др. — 2-е изд., перераб. —М.: Машиностроение, 1982.—432 с., ил. Учебно-методическое пособие к выполнению курсовой работы по дисциплине "Гидравлика и нефтегазовая гидромеханика"/ Л.Р.Байкова, Э.С.Бахтегареева, А.А.Гудникова. |
