Гидродинамика. Гидродинамика

• Название: Гидродинамика
• Дата: 18.04.2022
• Размер: 108.64 Kb.
• Имя файла: Гидродинамика.docx
• Тип: Реферат; #483641

ФГБОУ ВО Белгородский ГАУ им. В.Я. Горина

Инженерный факультет


РЕФЕРАТ

По дисциплине: «Гидравлика»

на тему: «Гидродинамика»

Выполнил:

студент группы 34-АИЭЛ-З

Кириченко Н.Н.

Проверил:

Вольвак С.Ф.


Майский 2020

Содержание
Введение……………………………………………………………………….3

Идеальная жидкость………………………………………………………….6

Стационарное течение………………………………………………………8

Уравнение Бернулли……………………………………………………….10

Следствие уравнения Бернулли…………………………………………12

Вязкость……………………………………………………………………….13

Уравнение Навье-Стокса…………………………………………………..16

Число Рейнольдса…………………………………………………………..16

Ламинарное течение………………………………………………………..18

Турбулентное течение………………………………………………………21

Подъемная сила……………………………………………………………..24

Список использованной литературы…………………………………….27

Введение

Гидродинамикой называется раздел гидравлики, рассматривающий законы движения жидкостей и их практические приложения. В гидростатике состояние жидкости характеризуется одним параметром – гидростатическим давлением (функцией координат точки в пространстве), а в гидродинамике движение жидкости характеризуется двумя параметрами – гидродинамическим давлением и скоростью. Кинематика жидкости обычно в гидравлике рассматривается совместно с динамикой и отличается от неё изучением видов и кинематических характеристик движения жидкости без учёта сил, под действием которых происходит движение, тогда как динамика жидкости изучает законы движения жидкости в зависимости от приложенных к ней сил.

При решении той или иной задачи в гидродинамике применяют основные законы и методы механики и, учитывая общие свойства жидкостей, получают решение, позволяющее определить скорость, давление и касательную напряжения в любой точке занятого жидкостью пространства. Это даёт возможность рассчитать, в частности, и силы взаимодействия между жидкостью и твёрдым телом. Главными свойствами жидкости, с точки зрения гидродинамики, являются её лёгкая подвижность, или текучесть, выражающаяся в малом сопротивлении жидкости деформациям сдвига, и сплошность (в гидродинамике жидкость считается непрерывной однородной средой); кроме того, в гидродинамике принимается, что жидкости не сопротивляются растяжению.

Основные уравнения гидродинамики получаются путём применения общих законов физики к элементарной массе, выделенной в жидкости, с последующим переходом к пределу при стремлении к нулю объёма, занимаемого этой массой. Одно из уравнений, называемое неразрывности уравнением, получается путём применения к элементу, выделенному в жидкости, закона сохранения массы: другое уравнение (или в проекциях на оси координат - три уравнения) получается в результате применения к элементу жидкости закона о количестве движения, согласно которому изменение количества движения элемента должно совпадать по величине и направлению с импульсом силы, приложенной к нему. Решение общих уравнений гидродинамики исключительно сложно и может быть доведено до конца не всегда, а только в небольшом числе частных случаев. Поэтому приходится упрощать задачи путём отбрасывания в уравнениях членов, которые в данных условиях имеют менее существенные значение для определения характера течения. Например, в ряде случаев можно с достаточной для практики точностью описать реально наблюдаемое течение, пренебрегая вязкостью жидкости; т. о., приходят к теории идеальной жидкости, которую можно применять для решения многих гидродинамических задач. В случае движения жидкостей с весьма большой вязкостью (густые масла и т.п.) величина скорости течения изменяется незначительно и можно пренебречь ускорением. Это приводит к др. приближённому решению задач гидродинамики.

В гидродинамике идеальной жидкости особенно важное значение имеет Бернулли уравнение, согласно которому вдоль струйки жидкости имеет место следующее соотношение между давлением р, скоростью v течения жидкости (с плотностью r) и высотой z над плоскостью отсчёта p + 1/2rv2 + rgz = const. (g - ускорение свободного падения). Это уравнение является основным в гидравлике.

Анализ уравнений движения вязкой жидкости показал, что для геометрически и механически подобных течений (см. Подобия теория) величина rvl/m= Re должна быть постоянной (l - характерный для задачи линейный размер, например радиус обтекаемого тела или сечения трубы и т.п., r, v и m - соответственно плотность, скорость, коэффициент вязкости жидкости). Эта величина называется Рейнольдса числом и определяет режим движения вязкой жидкости: при малых значениях Re (для трубопроводов при Re = vcpd/n £ 2300, где d - диаметр трубопровода, n = m/r) имеет место слоистое, или ламинарное течение, при больших значениях Re струйки размываются и в жидкости происходит хаотическое перемешивание отдельных масс; это т. н. турбулентное течение.

Решение основных уравнений гидродинамики вязкой жидкости оказалось возможным найти только для крайних случаев - для Re очень малых, что соответствует (при обычных размерах) большой вязкости, и для Re очень больших, что соответствует течениям жидкостей с малой вязкостью. В ряде технических вопросов особо важны задачи о течениях жидкостей с малой вязкостью (вода, воздух). В этом случае уравнения гидродинамики можно значительно упростить, выделив слой жидкости, непосредственно прилегающий к поверхности обтекаемого тела, в котором вязкостью пренебречь нельзя; этот слой называется пограничным слоем. За пределами пограничного слоя жидкость может рассматриваться как идеальная. Для характеристики движений жидкости, в которых основную роль играет сила тяжести (например, волны, образующиеся на поверхности воды при ветре, прохождении корабля и т.д.), в гидродинамике вводится др. безразмерная величина v2/gl = Fr, называемая числом Фруда.

Практические применения гидродинамики чрезвычайно разнообразны. Гидродинамикой пользуются при проектировании кораблей и самолётов, расчёте трубопроводов, насосов, гидротурбин и водосливных плотин, при исследовании морских течений и речных наносов, изучении фильтрации грунтовых вод и нефти в подземных месторождениях и т.п.

Идеальная жидкость

Идеальная жидкость — воображаемая (идеализированная) жидкость, в которой, в отличие от реальной жидкости, отсутствуют вязкость и теплопроводность. В идеальной жидкости отсутствует внутреннее трение, то есть, нет касательных напряжений между двумя соседними слоями.

Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.

Для кинематического описания течения идеальной жидкости воспользуемся методом Эйлера. Для этого выберем систему отсчета и зададим в ней поле скоростей, т. е. зависимость скорости каждой точки среды u от ее радиус-вектора и времени u = f(r, t). Мысленно проведем в жидкости линии тока.

Линии тока - линии, касательные к которым совпадают с направлением вектора скорости течения жидкости u.

При этом совершим построение так, чтобы густота линий тока (число линий, пронизывающих площадку единичной площади в перпендикулярном им направлении) была бы пропорциональна величине вектора скорости. Направление линий тока при этом должно совпадать с направлением u. Применение метода Эйлера дает наглядное представление о направлении и величине вектора скорости течения жидкости в разных точках. В случае стационарного течения картина линий тока не изменяется, а сами они совпадают с траекториями движения молекул жидкости.

Поверхность, образованная линиями тока, проведенными через все точки замкнутого контура, называется трубкой тока.

При стационарном течении жидкости ее молекулы не пересекают трубку тока.

Обычная динамика рассматривает, как правило, движение частиц и твердых тел. Характерной чертой этих физических объектов являлась их дискретность, т. е. расположение в строго определенных ограниченных и изменяющихся с течением времени, областях пространства. В противоположность этому жидкости и газы, если не вдаваться в молекулярную структуру вещества, можно рассматривать как непрерывные среды, применяя к описанию их движения характерные методы.

Стационарное течение

Рассмотрим течение идеальной жидкости внутри некоторой трубки тока, обладающей такими сечениями, что скорость молекул жидкости в любой точке каждого из них одинакова. Так как идеальная жидкость несжимаема, то ее масса, сосредоточенная между сечениями S₁ и S₂ трубки тока, с течением времени не изменяется. Следовательно, объемы жидкости dQ, протекшие через эти сечения за промежуток времени dt, будут равны. Поскольку dQ = S·v·dt, то выполняется соотношение: S·v = const

Это выражение называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости.

Обычно жидкости при внешнем воздействии приходят в движение, при этом давление и скорость ее частиц, вообще говоря, могут сложным образом меняться от точки к точке внутри объема текущей жидкости. Поясним сказанное примером. Подключим горизонтальную стеклянную трубку переменного сечения при помощи резинового шланга к водопроводному крану.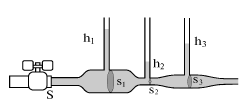



Если напор воды остается постоянным, то течение воды можно считать установившимся (или стационарным). В этом случае масса воды M, протекающая в единицу времени через сечения с площадями S₁ и S₂ будет одинаковой, поэтому имеет место равенство

m = ρ₁v₁S₁ = ρ₂v₂S₂,

где (ρ и v - плотность и скорость жидкости в этих сечениях. Если жидкость несжимаема (ρ₁ = ρ₂), то мы приходим в условие постоянства объема жидкости (условие несжимаемости), протекающего через сечения S₁ и S₂:

V = v₁S₁ = v₂S₂

Следует отметить, что условия постоянства массы и несжимаемости жидкости записаны для случая, когда скорости всех частиц жидкости одинаковы в поперечном сечении трубки.

Для графического изображения течения жидкости удобно использовать линии тока - линии, касательная к которым в каждой точке совпадает с вектором скорости частицы. Легко видеть, что в сечении S скорости частиц различны, и объем протекающей жидкости через это сечение не может быть записан в виде V = v₁S₁ = v₂S₂.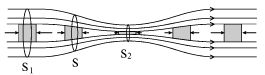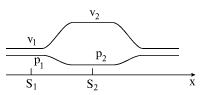



Далее отметим, что по мере приближения к узкому сечению S₂ частица, деформируясь, ускоряется, а при удалении от S₂ - замедляется. Эти ускорения могут обеспечить лишь силы давления f_i = - p_in, показанные на рисунке маленькими стрелками. Из рисунка ясно, что давление в жидкости по мере приближения к S₂ падает. А затем возрастает. Это легко проверить, если сравнить уровни h₁ и h₂ жидкости в манометрических стеклянных трубках, впаянных в горизонтальную трубку вблизи сечений S₁ и S₂. Поскольку p₁ = ρgh₁, p₂ = ρgh₂, то p₁ > p₂, т.к. h₁ > h₂. На рисунке ниже качественно изображено распределение скоростей и давлений вдоль оси трубки.

Уравнение Бернулли

Рассмотрим стационарное течение идеальной жидкости плотности ρ в однородном поле силы тяжести под действием сторонних сил. Пусть под действием перепада давлений p₁ - p₂, вызванного внешними сторонними силами, за интервал времени dt молекулы жидкости, находящиеся в сечениях трубки тока S₁ и S₂, сместились вдоль нее соответственно на расстояния dL₁ и dL₂ (см. рис.14.5).

Для описания движения воспользуемся энергетическими соображениями. Рассмотрим жидкость, сосредоточенную между сечениями трубы S₁ и S₂. Согласно закону изменения полной механической энергии ее приращение равно работе внешних сторонних A_ст и внутренних неконсервативных сил, действующих на рассматриваемый объем жидкости. Последняя из этих составляющих в отсутствие внутреннего трения у идеальной жидкости равняется нулю и, следовательно,

Δ=A_ст

Исходя из того, что работу совершают только тангенциальные составляющие сил, получим выражение для расчета работы по перемещению выделенного объема жидкости:

Aст = p₁·S₁·dL₁ - p₂·S₂·dL₂

Из этой формулы и уравнения неразрывности струи cледует, что

A_ст = (p₁ - p₂)·dV,

где dV - объем жидкости, протекающей через сечение трубки тока за время dt

Приращение полной механической энергии ΔE найдем как сумму приращений кинетической и потенциальной энергий в 1-м и 2-м сечениях трубки тока:

ΔE = (ρ·ΔV·v₂²/2 - ρ·ΔV·v₁²/2) + (ρ·ΔV·g·h₂ - ρ·ΔV·g·h₁).

Отсюда, с учетом произвольности выбора сечений 1 и 2, получим, что для выбранной трубки тока справедливо следующее соотношение:

ρ·v²/2 + p + ρ·g·h = соnst

Это соотношение, называемое уравнением Бернулли, получено для достаточно узкой трубки тока и, строго говоря, справедливо, когда трубка тока переходит в линию тока. Оно хорошо выполняется для реальных жидкостей, обладающих малым внутренним трением.

Это уравнение описывает стационарное течение несжимаемой жидкости (иногда употребляют термин "идеальной жидкости"), и играет фундаментальную роль в гидродинамических исследованиях. Если нам известно давление p₁, скорость v₁ в некотором сечении трубки тока, находящемся на высоте h₁, то в любом другом сечении на высоте h величины p и v связаны соотношением

ρ·v²/2 + p + ρ·g·h = ρ·v₁²/2 + p₁ + ρ·g·h₁

Рассмотрим более подробно физический смысл входящих в уравнение Бернулли членов. Так, статическое давление p численно равно работе сил давления, совершаемых над единичным объемом жидкости; динамическое давление ρv²/2 есть кинетическая энергия единицы объема, а величина ρgh является потенциальной энергией единичного объема в поле силы тяжести

Давление p - это статическое давление, которое получит манометр, находящийся в жидкости и движущийся вместе с нею, ρv²/2 - это динамическое давление, смысл которого будет раскрыт позднее. Заметим, что в покоящейся жидкости предыдущее равенство описывает гидростатическое распределение давлений.

Следствие уравнения Бернулли

В данном случае уравнение Бернулли примет вид:

ρ·v²/2 + p = соnst.

Отсюда следует, что в областях трубки с большей скоростью течения жидкости давление меньше. Согласно уравнению неразрывности струи скорость течения жидкости u больше в местах с меньшим сечением трубы, следовательно, давление по мере перехода к более узким ее участкам уменьшается. Образующийся при этом перепад давлений заставляет жидкость двигаться вдоль трубы с ускорением. Обратите внимание, что зависимости скорости и давления от координаты вдоль оси трубы, а также направление ускорения не зависят от направления скорости течения жидкости.

Пусть идеальная жидкость вытекает из сосуда через отверстие малого диаметра, просверленное у его дна. Все линии тока проходит через свободную поверхность, находящуюся на высоте h над дном сосуда, и отверстие, причем постоянная в уравнении Бернулли будет равна для всех линий тока. Рассмотрим одну из этих линий, учитывая, что скорость течения жидкости у свободной поверхности пренебрежимо мала по сравнению со скоростью вытекания жидкости из отверстия. Учтя вышеизложенное и применив уравнение Бернулли к линии тока на уровне свободной поверхности жидкости и отверстия получим:

p_атм + ρ·g·h = p_атм + ρ·v²/2

Отсюда можно получить выражение для расчета скорости истечения жидкости через отверстие.

v = (2·g·h)^1/2

Эта формула носит название формулы Торичелли, поскольку была получена Торичелли, жившим до Бернулли. Сразу бросается в глаза, что скорость истечения жидкости из сосуда такая же, как и при ее свободном падении с высоты h. В этом нет ничего удивительного, поскольку вязкостью мы пренебрегли, а работа сил атмосферного давления над трубкой тока равна нулю. Поэтому, как и при свободном падении тел в отсутствие сопротивления воздуха, приращение кинетической энергии равно работе силы тяжести.

Если создать очень высокое избыточное давление, например, 5000 атм = 5 · 10 Н/м², то скорость истечения воды v = 1000 м/с. Если такую струю направить на какой-либо твердый материал, то его поверхность будет подвержена гидродинамическому давлению Такое огромное давление в ряде случаев может превосходить предел прочности некоторых материалов, и последние будут разрушаться под действием струи. Со второй половины 80-х годов получило развитие новое направление в обработке материалов - гидрорезание. В этой технологии водяной нож - высоко-скоростная струя воды с диаметром иглы - легко режет материалы толщиной в несколько сантиметров со скоростью резания несколько десятков сантиметров в минуту. Для резки металлов, твердых сплавов, бетона и других материалов в струю добавляют абразивный порошок. Это позволяет значительно увеличить гидродинамическое давление и повысить производительность и возможности гидрорезания.

Вязкость

Идеальная жидкость является физической моделью, позволяющей понять суть явления в некотором приближении. Всем реальным жидкостям присущи вязкость или внутреннее трение, что приводит к появлению у них принципиально новых свойств. В частности, возникшее в жидкости движение после прекращения действия причин, его вызвавших, постепенно замедляется. Следовательно, жидкость при своем движении в трубе испытывает сопротивление. Такого рода сопротивление называют вязким, подчеркивая тем самым отличие от сопротивления в твердых телах.

В твердых телах в случае попытки изменения их формы (например, при сдвиге одной части тела относительно другой) возникает сила упругой деформации сдвига, пропорциональная смещению атомов, находящихся в узлах кристаллической решетки соседних атомных слоев. В жидкости эта сила пропорциональна величине изменения скорости, наблюдающейся при переходе между соседними слоями взаимодействующих молекул.

Ранее мы рассматривали движение жидкости и газа в пренебрежении силами вязкого трения. Между тем, эти силы, действующие между частицами движущейся жидкости, могут кардинальным образом повлиять как на распределение скоростей в потоке жидкости, так и на обтекание жидкостью тел, помещенных в движущийся поток.

Еще Ньютон установил опытным путем, что при скольжении друг относительно друга двух параллельных плоскостей, пространство между которыми заполнено жидкостью, силы вязкого трения препятствуют этому скольжению. Так, при движении со скоростью v верхней плоскости с площадью S относительно нижней, возникает сила вязкого трения, направленная против движения и равная F_т = μS ^v/_h.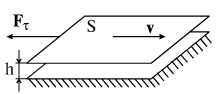



Эта сила пропорциональна площади S и изменению скорости на единицу длины в поперечном направлении ^v/_h (градиенту скорости в направлении перпендикулярном движению) и зависит также от вязкости жидкости μ.

Вышепривёдённая формула справедлива, если расстояние h между пластинами значительно меньше их линейных размеров . Важно отметить, что частицы жидкости, прилегающие к верхней пластине, движутся вместе с нею со скоростью v (увлекаются пластиной). Напротив, частицы жидкости вблизи нижней (неподвижной) пластины находятся в покое (прилипают к пластине). Если мысленно разбить жидкость на параллельные плоские слои, движущиеся равномерно, то нетрудно понять, что каждый вышележащий слой увлекает за собой нижний соседний слой с силой F_т. В свою очередь, этот нижний слой тормозит движение верхнего слоя с силой, численно равной F_т. На каждый слой действует сверху и снизу две равные, но противоположные силы. Скорость слоев нарастает линейно с их высотой (см. рисунок ниже), а сила трения передается от одному слоя к другому. Как результат, усилие F = F_т, приложенной к верхней пластине, передается на нижнюю пластину. Коэффициент вязкости среды определяется экспериментально, например, по скорости ее истечения через трубку известных размеров. Как показывает опыт с нагреванием, вязкость жидкости уменьшается, а газов - увеличивается.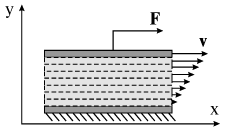

Уравнение Навье-Стокса

Для анализа течения вязкой жидкости в гидро динамике используется уравнение Навье-Стокса:



где — оператор Гамильтона, Δ — оператор Лапласа, — вектор скорости, t — время, ν — коэффициент кинематической вязкости, ρ — плотность, P — давление, — вектор плотности массовых сил. Уравнение Навье-Стокса является основным при расчете движения вязкой несжимаемой жидкости. Однако в общем случае оно не решается методами современной математики, и на практике приходится ограничиваться решением лишь частных задач. Одной из таких задач является течение невязкой несжимаемой жидкости, подчиняющееся уравнению Бернулли. Ранее мы получили условие, при котором сжимаемостью жидкости или газа можно пренебречь. Теперь мы выясним, в каких случаях можно пренебречь действием сил вязкости.

Число Рейнольдса

Течение вязкой жидкости по трубам в зависимости от ряда условий может быть ламинарным (или слоистым) и турбулентным (или вихревым). В случае ламинарного течения все молекулы жидкости движутся параллельно оси трубы и, находясь на одинаковом расстоянии от осевого центра трубы, имеют равные скорости

Для турбулентного движения характерно наличие нормальной (перпендикулярной направлению течения жидкости) составляющей скорости движения молекул и резкий спад скорости течения при приближении к границам. Траектория движения молекул представляет собой сложную кривую линию.

Характер течения можно установить, пользуясь безразмерной величиной - числом Рейнольдса:

Re = ρ·v_ср·r/μ,

где ρ - плотность жидкости;
v_ср - средняя (по сечению трубы) скорость потока; μ - коэффициент вязкости жидкости; r - характерный геометрический размер, в частности, радиус сечения цилиндрической трубы

Число Рейнольдса характеризующет отношение сил инерции и сил вязкости. Таким образом, текущую жидкость можно рассматривать как невязкую, если число Рейнольдса для такого течения Re>1. Однако и в этом случае вязкость играет вспомогательную роль. При не очень высоких скоростях течения силы вязкости "гасят" компоненты скорости жидкости, поперечные к потоку, препятствуя, тем самым, возникновению неустойчивого течения (см. ниже).

Дадим некоторые оценки течения жидкости по круглой трубе радиуса R. Число Рейнольдса в этом случае Re = ρ·v_ср·R/μ. Если принять радиус трубы R = 1 см и скорость течения v = 1 см/с, то для воды (ρ=103 кг/м³, при t > = 15) число Re=86. Это означает, что силы вязкости не существенны, и воду можно рассматривать как невязкую жидкость. Однако это приближение становится несправедливым, если радиус трубки уменьшить на два порядка, и Re=0,86 < 1. При таком течении распределение давлений и скоростей в потоке уже не подчиняется уравнению Бернулли. Еще в большей степени это относится к вязкому глицерину (ρ=1,4 кг/(м·с)). При течении воздуха по трубе (ρ=1,3 кг/м³, ρ=1,8·10^-5 кг/(м*с)) число Рейнольдса приблизительно на порядок меньше, чем при аналогичном течении воды. Это указывает на то, что силы вязкости при течении воздуха и других газов играют большую роль, чем при аналогичном течении воды.

Ламинарное течение

Гидродинамика ламинарных течений изучает поведение жидкости в нетурбулентном режиме. Во многих случая уравнения гидродинамики имеют достаточно простой вид и могут быть решены точно. Некоторые наиболее важные задачи этого раздела гидродинамики:

• 
  стационарное течение идеальной несжимаемой жидкости при различных граничных условиях
  
• 
  стационарное течение вязкой жидкости, уравнение Навье-Стокса
  
• 
  волны на поверхности идеальной несжимаемой жидкости и прочие нестационарные явления
  
• 
  ламинарное обтекание конечных тел
  
• 
  течения в различных несмешивающихся жидкостях, тангенциальные разрывы и их устойчивость
  
• 
  струи, капли и прочие течения конечных размеров
  

Ламинарное течение наблюдается при малых значениях числа Рейнольдса. Начиная с некоторого определенного значения Re, называемого критическим, течение приобретает турбулентный характер. Для воды в гладких круглых трубах Re_кр = 2000.

В случае ламинарного течения жидкости согласно третьему закону Ньютона более медленные слои за счет вязкого трения тормозят более быстрые и наоборот, быстрые ускоряют медленные. Причем молекулы стенок трубы не имеют тангенциальной составляющей скорости, и пограничный слой жидкости жестко "прилипает" к ее стенкам. Таким образом, скорость движения отдельных равноудаленных от оси трубы цилиндрических слоев жидкости возрастает от нулевого до максимального значения по мере удаления от стенок трубы (см. рисунок). При стационарном течении распределение скоростей по сечению трубы имеет параболический характер.

Рассчитаем поток или количество жидкости, протекающей через поперечное сечение трубы S в единицу времени. В случае однородного поля скоростей величина потока Q зависит от скорости течения жидкости u по формуле Q = v·S.

Рассчитаем поток жидкости dQ, вытекающей из цилиндрического слоя толщиной dr, расположенного на расстоянии r от оси трубы, а затем проведем интегрирование по всем слоям от 0 до R.

dQ = v(r)·dS = v(r)·2π·r·dr,

где dS - площадь поперечного сечения цилиндрического слоя.

Для ответа на поставленный вопрос необходимо найти зависимость v(r). Выделим цилиндр радиусом r и длиной L, расположенный симметрично осевой линии трубы. При стационарном течении скорость течения со временем не изменяется, следовательно, сумма всех сил, действующих на все объемы жидкости, равна нулю. На выделенный цилиндр действуют следующие силы: сила давления, равная произведению разности внешних давлений на площадь поперечного сечения выделенного объема, и сила вязкого трения, действующая на боковую поверхность цилиндра радиусом r, рассчитываемая по формуле Ньютона. Таким образом,

(p₁ - p₂)π·r² = μ·|dv/dr|·2π·r·L.

Преобразуя предыдущее уравнение, получим, что

- dv = (p₁ - p₂)·r·dr/(2μ·L)

Проинтегрировав это выражение с учетом граничных условий v = 0 при r = R,

получим формулу для расчета скорости слоев жидкости, расположенных на расстоянии r от оси трубы:

v(r) = (p₁ - p₂)·(R² - r²)/(4μ·L)

Максимальная скорость, достигаемая в центре трубы v₀, равна:

v₀ = (p₁ - p₂)·R²/(4μ·L)

Проведя интегрирование по радиусу, найдем выражение для потока жидкости, вытекающей из трубы:

Q = (p₁ - p₂)·π·R⁴/(2μ·L)

Это соотношение называется формулой Пуазейля.

Из него следует, что поток в случае стационарного течения жидкости обусловлен перепадом давлений, зависит от геометрии трубы и свойств жидкости. Следует обратить внимание на существенную зависимость пропускной способности трубы от ее радиуса R. При заданном давлении на входе водопроводной сети увеличение диаметра труб вдвое влечет увеличение их пропускной способности в 16 раз!

Формулой Пуазейля пользуются при расчетах показателей транспортировки жидкостей и газов в трубопроводах различного назначения. Ламинарный режим работы нефте- и газопроводов является наиболее выгодным в энергетическом отношении. Так, в частности, коэффициент трения при ламинарном режиме практически не зависит от шероховатости внутренней поверхности трубы (гладкие трубы).

Пользуясь формулой Пуазейля можно определить вязкость жидкости. Так, например, в опыте, изображенном на рисунке ниже, легко измерить разность давлений и расход жидкости и при известном радиусе горизонтальной трубки посчитать вязкость жидкости Однако более удобно вязкость жидкости определять по методу Стокса, измеряя время падения шарика в этой жидкости.

Параболический профиль скорости слоев, как нетрудно подсчитать, будет и при течении жидкости между двумя пластинами . Если этот рисунок разрезать посередине на высоте и наклонить нижнюю пластину под углом α, то мы получим картину слоистого течения воды в реке под действием силы тяжести. Вместо перепада давления dp/dx мы можем использовать компоненту силы тяжести F_x = ρg sin α при расчете профиля скоростей течения.

Турбулентное течение

При достаточно малых скоростях потока жидкости или газа течение всегда является ламинарным, однако при увеличении скорости всегда происходит переход в турбулентное течение, которое является уже существенно нестационарным и пространственно-неоднородным, поскольку скорость частиц жидкости, давление и другие характеристики среды изменяются во времени и пространстве нерегулярно, случайным образом даже при постоянных внешних условиях.

Основным параметром, с помощью которого описываются ламинарное течение, турбулентное течение и переход от ламинарного течения к турбулентному течению, является число Рейнольдса Re.

Параметр Re - безразмерный, он определяет отношение сил инерции к вязким силам в уравнении Навье-Стокса. Существует критическое число Рейнольдса Reкр, такое, что при Re < Reкр поток будет ламинарным, а при Re > Re_кр - турбулентным.

Переход ламинарного течения в турбулентное легко фиксируется при наблюдении окрашенных струй. При ламинарном течении струя имеет вид ровной линии. При переходе к турбулентному течение струю завихряется, краска размывается, постепенно расплываясь по всему сечению трубки.

Изменение числа Re при течении в одной и той же трубке можно осуществлять как изменением скорости потока (перепада давления на концах трубки), так и изменением вязкости жидкости, например, нагревая ее или заменяя на другую.

Если увеличивать скорость потока так, что число Рейнольдса станет несколько больше единицы, то увидим, что поток изменился. За сферой возникают вихри. Обычно считают, что циркуляция нарастает постепенно. Когда Re принимает значения от 10 до 30, поток меняет свой характер.

Когда число Рейнольдса проходит значение в районе 40, характер движения претерпевает неожиданное и резкое изменение. Один из вихрей за цилиндром становится настолько длинным, что отрывается и плывет вниз по течению вместе с жидкостью. При этом жидкость за цилиндром снова закручивается и возникает новый вихрь. Вихри отслаиваются то с одной, то с другой стороны и в какой-то момент вытягиваются вихревым следом за цилиндром. Такой поток вихрей называется цепочкой Кармана. Она всегда появляется для чисел Рейнольдса Re > 40.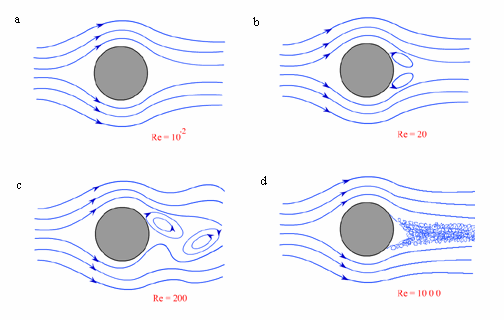



а) ламинарный режим, Re < 1;
b) первая стадия неустойчивости, 1 < Re <40;
c) вторая стадия неустойчивости (вихревая дорожка), Re > 40;
d) развитая турбулентность, Re > 10³.

1. При малых значениях Re ( Re < 1 ) имеет место ламинарное обтекание цилиндра (рис. а).

2. При 1 < Re < 40 вблизи первого критического значения значения Re = 1 исходный поток становится неустойчивым, однако новый тип течения окончательно определяется при Re > 10: за цилиндром образуются два вихря, но течение остается стационарным и ламинарным.

3. При Re > 40 стационарное движение теряет устойчивость. Вихри удлиняются, отрываются и уплывают с потоком жидкости. В результате за цилиндром образуется т.н. вихревая дорожка. Движение становится нестационарным, но периодическим.

4. При Re > 1000 вихри уже не успевают формироваться и заменяются быстротурбулизирующимися областями. При Re 10⁴ движение становится нерегулярным; при Re 10⁵ турбулентная область продвигается вплоть до поверхности цилиндра.

Подъемная сила

Рассмотрим движение твердого тела относительно жидкости, находящейся в состоянии покоя в некоторой ИСО. Исходя из принципа относительности эта задача эквивалентна обтеканию неподвижного тела стационарным потоком жидкости.

Силу, действующую на неподвижное тело в направлении потока, называют лобовым сопротивлением, а силу, действующую на него в перпендикулярном направлении, - подъемной силой.

Cтационарное обтекание твердого тела потоком идеальной жидкости не вызывает появления подъемной силы и лобового сопротивления. Покажем это на примере симметричного, покоящегося относительно наблюдателя, тела. В данном случае линии тока относительно вертикальной оси, проходящей через центр масс тела перпендикулярно направлению потока жидкости, симметричны. Следовательно, для симметричных элементарных пространственных областей значения величины скоростей в трубке тока равны по величине. Тогда, исходя из уравнения Бернулли, давления в этих областях попарно равны и лобовое сопротивление отсутствует.

В виду симметрии задачи (но уже по отношению к оси, параллельной потоку) равна нулю и подъемная сила.

Иначе дело обстоит для вязкой жидкости или газа. Пусть тело, вращающееся относительно своего центра масс, погружено в газовый поток. Прилегающие к телу слои молекул участвуют в двух движениях: вращательном, обусловленном наличием вязкого трения между телом и газом, и поступательном, связанным с движением газа вдоль оси трубы.

Подъемная сила создается не столько повышением давления под крылом, сколько падением давления над крылом. Эта сила пропорциональна динамическому давлению, площади крыла S и вычисляется по формуле

F_п = С_ySρv²/2

где С_y - коэффициент подъемной силы, зависящий от угла атаки α Если бы воздух обтекал крыло безотрывно, то коэффициент С_y возрастал бы пропорционально α. Однако опыты показывают, что при углах атаки α = 12° - 18° (в зависимости от формы крыла) подъемная сила достигает максимума, а затем начинает падать.

Угол атаки, при котором коэффициент С_y максимален, называется посадочным или критическим, а соответствующий коэффициент также называется посадочным. У обычных крыльев C_yпос = 1,2 - 1,6. Срыв потока и образование завихрения приводит к повышению давления над крылом и уменьшению подъемной силы.

Коэффициент определяет посадочную скорость самолета v_пос, определяемую из равенства подъемной силы весу самолета. Для снижения скорости посадки необходимо предотвратить срыв потока при увеличении угла атаки. В современной авиации этого добиваются применением на крыльях посадочных приспособлений - подкрылков и закрылков, выдвигаемых механически из крыла при посадке самолета.


Список использованной литературы

1. Трофимова В.И. Курс физики: Учеб. Пособие для вузов.5-е изд., стер. – М.: Высш. Шк., 1998. – 542 с.

2. Савельев И.В. Курс общей физики: Учеб пособие. Т. 1

3. «Энциклопедия Кирилла и Мефодия» в электронном виде, 2005.