Гидрогазодинамика. nchti_Рузанова_Гидрогазодинамика_уч_пособие (1). Гидрогазодинамика учебное пособие
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
18. Приближенное моделирование. АвтомодельностьПри моделировании многих процессов химической технологии не удается соблюсти полное подобие, т. е. равенство всех определяющих критериев подобия для натуры и модели, как этого требует третья теорема подобия. Поэтому при проведении моделирования часто можно удовлетвориться соблюдением не полного подобия, а лишь подобия тех факторов, которые наиболее значительно влияют на исследуемый процесс, т. е. осуществить приближенное моделирование. Если какой-либо параметр не влияет на протекание процесса, то процесс называют автомодельным по отношению к этому параметру. Автомодельность может наступить при изменении условий протекания процесса. Типичным примером служит сопротивление сил трения движению вязкой жидкости. 19. Сопротивление трения в гладких и шероховатых трубахГидравлическое сопротивление трубопровода – это потери напора жидкости при ее течении в трубопроводе. Определение потерь напора hп необходимо для расчета затрат энергии для перемещения жидкости (с помощью насосов, компрессоров). Потери напора в трубопроводе расходуются на преодоление сил: путевых (линейных) сопротивлений (сопротивление трения); местных сопротивлений: 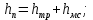 (92) (92)В общем случае, путевые сопротивления зависят от режима течения жидкости и от шероховатости стенок труб. Для определения потерь напора на трение при равномерном движении жидкости в круглых трубах применяют формулу Дарси-Вейсбаха: 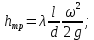 (93) (93)где l, d – длина и диаметр трубы; ω – средняя скорость потока; λ – коэффициент гидравлического трения (коэффициент путевых сопротивлений). λ показывает, какая доля динамического напора теряется на участке, равному диаметру трубы. Для некруглых труб в уравнение Дарси-Вейсбаха вместо диаметра d подставляют эквивалентный диаметр dэ. Зависимость 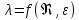 для труб с искусственной однородной шероховатостью (наклеивались зерна песка на внутреннюю поверхность труб) исследовал Никурадзе в 1932 г. Никурадзе получил график: для труб с искусственной однородной шероховатостью (наклеивались зерна песка на внутреннюю поверхность труб) исследовал Никурадзе в 1932 г. Никурадзе получил график: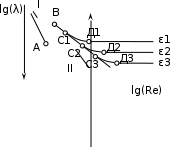 Рис.25. График Никурадзе ε1 > ε2 > ε3 (относительная шероховатость). На графике Никурадзе можно выделить пять зон: ламинарный режим (Re ≤ 2320) 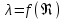 – прямая I; – прямая I;переходная из ламинарного в турбулентный (Re=2320-3000); область «гидравлически гладких» труб при турбулентном режиме: 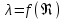 , прямая II; 3000 < Re < , прямая II; 3000 < Re < 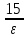 ; ;область шероховатых труб (доквадратичная область «смешанного трения») при турбулентном режиме: 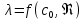 ; прямая II; кривые СiДi; ; прямая II; кривые СiДi;область «вполне шероховатых труб» (квадратичная или автомодельная область) 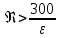 при турбулентном режиме: при турбулентном режиме: 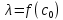 . Горизонтальные прямые – вправо от точек Дi. . Горизонтальные прямые – вправо от точек Дi.Пока выступы шероховатости полностью погружены в ламинарный пограничный слой ( 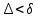 ), жидкость плавно обтекает эти выступы и влиянием шероховатости на величину λ можно пренебречь. В этом случае коэффициент λ зависит только от числа Re и определяется для гидравлически гладких труб (зоны 1-3). ), жидкость плавно обтекает эти выступы и влиянием шероховатости на величину λ можно пренебречь. В этом случае коэффициент λ зависит только от числа Re и определяется для гидравлически гладких труб (зоны 1-3).С увеличением Re толщина слоя δ уменьшается. При 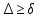 ламинарное течение нарушается и λ начинает зависеть от шероховатости (4-ая зона), хотя еще и продолжает зависеть от Re. ламинарное течение нарушается и λ начинает зависеть от шероховатости (4-ая зона), хотя еще и продолжает зависеть от Re.Если число Re очень велико и 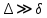 , то λ зависит только от шероховатости (5-ая зона). , то λ зависит только от шероховатости (5-ая зона).В практических расчетах для определения λ используются следующие формулы. 1-ая зона – ламинарный режим: 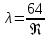 – формула Пуазейля. – формула Пуазейля.2-ая зона. Поток является неустойчивым, т.к. небольшое изменение Re приводит к сильному изменению сопротивления. Нерасчетная область. 3-я зона – гидравлически гладкие трубы. 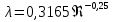 – формула Блазиуса. – формула Блазиуса.4-ая зона – частично шероховатые трубы. 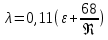 – формула Альштуля. – формула Альштуля.5-ая зона – шероховатые трубы. 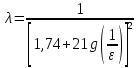 – формула Прандля-Никурадзе. (94) – формула Прандля-Никурадзе. (94)Или 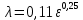 – формула Шифринсона. – формула Шифринсона.Все эти формулы справедливы для изотермических условий ( 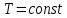 ). При переменной температуре в эти формулы вводятся поправочные множители (т.к. ). При переменной температуре в эти формулы вводятся поправочные множители (т.к. 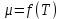 ). ).По опытным данным, для новых стальных труб 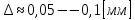 ; для стальных труб после некоторой эксплуатации ; для стальных труб после некоторой эксплуатации 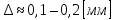 ; для старых чугунных и стальных труб ; для старых чугунных и стальных труб 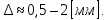 |
