Гидрогазодинамика. nchti_Рузанова_Гидрогазодинамика_уч_пособие (1). Гидрогазодинамика учебное пособие
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
14. Условия и теоремы подобия. Подобное преобразование дифференциальных уравненийОдин из основных принципов теории подобия заключается в выделении из класса явлений группы подобных явлений. Например, такие разные, на первый взгляд, явления, как движение окружающего нас атмосферного воздуха и движение капельной жидкости по трубопроводу в основе своей однородны, так как по существу представляют собой перемещение вязкой жидкости под действием разности давлений; поэтому данные явления описываются едиными уравнениями Навье-Стокса и принадлежат к одному классу. Вместе с тем движение вязких жидкостей (капельных и упругих) через трубы и аппараты различного профиля и размера составляет группу подобных явлений, входящих в этот класс. Подобными называют явления, для которых постоянны отношения характеризующих их сходственных величин. Условия подобия рассмотрим первоначально на простейшем примере геометрического подобия. Как известно из геометрии, из класса однородных плоских фигур (треугольников, многоугольников и др.) можно выделить группы подобных фигур, например, треугольников, сходственные линейные размеры которых параллельны, а отношения этих размеров постоянны. Подобные фигуры отличаются друг от друга только масштабом и могут быть получены одна из другой умножением сходственных размеров одной из них на некоторый постоянный масштабный множитель. Безразмерные масштабные множители, выражающие отношения однородных сходственных величин подобных фигур (или любых подобных систем), называются константами подобия. Например, если размеры сторон одного треугольника равны а', b' и с', а размеры сходственных сторон подобного ему треугольника составляют а", b" и с", то 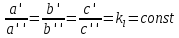 где kl – константа геометрического подобия (индекс l указывает на подобие линейных размеров). Подобие может быть охарактеризовано также инвариантами подобия, которыми, в отличие от констант подобия, выражающих отношения сходственных величин разных фигур, называют безразмерные отношения каких-либо двух размеров одной из фигур, равные отношению сходственных размеров подобной фигуры. Так, для рассматриваемых подобных треугольников 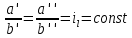 где il – инвариант геометрического подобия. Инварианты подобия представляют собой выражения величин в относительных единицах, т. е. в безразмерном виде. Например, в данном случае одна из сторон (а) подобных треугольников выражена в относительных единицах, причем в качестве масштаба для ее измерения выбрана их другая сторона (b). В тех же единицах, очевидно, можно выразить также третью сторону (с) подобных треугольников. Для подобия физических явлений соблюдение геометрического подобия систем (аппаратов), в которых они протекают, является необходимым, но не достаточным условием. При подобии физических процессов должны быть подобны все основные физические величины, влияющие на процесс. Эти величины изменяются по мере протекания процесса (во времени) и в различных точках аппарата, т. е. в пространстве. Поэтому технологические процессы подобны только при условии совместного соблюдения геометрического и временного подобия, подобия полей физических величин, а также подобия начальных и граничных условий. Сформулируем эти условия на примере подобного движения вязкой жидкости в натуре (в производственном трубопроводе) и в ее уменьшенной модели. Для этого рассмотрим любые сходственные точки, лежащие, например, на оси труб: A0' и A0" (на входе), а также A1" и A1", A2" и A2" и т. д. Геометрическое подобие соблюдается при равенстве отношений всех сходственных линейных размеров натуры и модели: 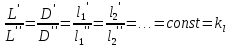 ; (62) ; (62)где L' и L" – длина натуры и модели; D' и D" – диаметр натуры и модели; l1', l1", l2', l2" и т. д. – пути, проходимые сходственными частицами жидкости от входа до произвольной точки, сходственной для натуры и модели. При подобном движении сходственных частиц их траектории в натуре и в модели также должны быть подобны. Это условие иногда называют кинематическим подобием. Постоянная величина kl характеризующая соотношение между геометрическими параметрами подобных систем и позволяющая перейти от размеров одной системы к размерам другой, представляет собой, как указывалось, константу геометрического подобия. 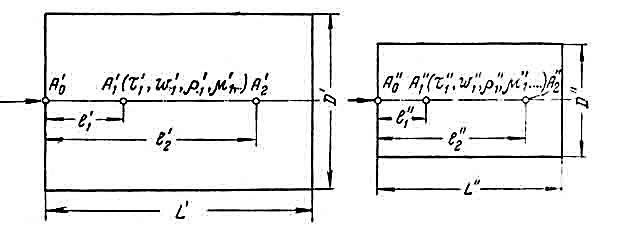 Рис.24. К формулировке условий подобия потоков натуре и в модели Временное подобие характеризуется тем, что сходственные частицы в геометрически подобных системах, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути за промежутки времени, отношение которых является постоянной величиной, т. е. 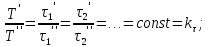 (63) (63)где Т', Т" – время прохождения сходственными частицами всего трубопровода (натуры и модели соответственно); τ1', τ1", τ2', τ2" и т. д. – время прохождения сходственными частицами подобных путей l1', l1", l2', l2" и т. д.; kτ – константа временного подобия. При соблюдении геометрического и временного подобия будет соблюдаться также подобие скоростей: 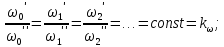 (64) (64)Подобие физических величин предполагает, что для двух любых сходственных точек натуры и модели, размещенных подобно в пространстве и времени (т. е. при соблюдении геометрического и временного подобия), отношения физических свойств являются величинами постоянными. Так, например, если движущиеся по трубопроводам жидкости имеют вязкость µ, плотность ρ и т. д., то для сходственных точек натуры и модели 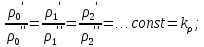 (65) (65)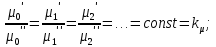 (66) (66)и т.д. Подобие начальных и граничных условий предполагает, что отношения основных параметров в начале на границе натуры и модели являются соответственно величинами постоянными. Иными словами, для начальных и граничных условий должно соблюдаться геометрическое, временное и физическое подобие, как и для других сходственных точек натуры и модели. Константы подобия kl, kτ, kω, kρ, kµ т.д., выражающие отношения различных одноименных величин в натуре и в модели, постоянны для различных сходственных точек подобных систем, но изменяются в зависимости от соотношения размеров натуры и модели. Отметим еще одно важное свойство констант подобия: входящие в них одноименные величины могут взаимно заменяться. Поэтому отношения приращений этих величин можно заменять отношениями самих величин. Например: 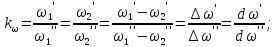 (67) (67)и т.д. Подобие потоков в натуре и модели можно охарактеризовать также с помощью инвариантов подобия, выражая все подобные величины в относительных единицах, т. е. в виде отношений сходственных величин в пределах каждой системы. Так, из уравнения следует: 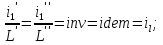 (68) (68)причем inv, или idem, – означает инвариантно, или «одно и то же». Величина il представляет собой инвариант подобия геометрических величин. При выражении любой величины в относительных единицах в качестве масштаба ее измерения может быть выбрано значение этой величины в любой точке системы. Например, за масштаб вместо длины труб L' и L" можно принять их диаметры и т. д. Аналогично следует: 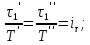 (69) (69)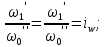 (70) (70)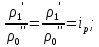 (71) (71)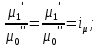 (72) (72)Инварианты подобия il,iτ, iω, iρ, iµ, и т. д. могут быть неодинаковы для различных сходственных точек подобных систем, но не зависят от соотношения размеров натуры и модели. Это означает, что при переходе от одной системы к другой, ей подобной, инварианты подобия не меняют своих значений. Приведенные выше инварианты подобия, выраженные отношением двух однородных физических величин (параметров), называются параметрическими критериями, или симплексами. Однако инварианты подобия могут быть выражены также отношениями разнородных величин, т. е. представлять собой безразмерные комплексы этих величин. Например, как показано ниже, для сходственных точек подобных потоков в трубопроводах равны инварианты подобия, состоящие из различных физических величин, или безразмерные комплексы, являющиеся уже известным нам критерием Рейнольдса: 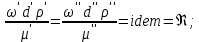 Если инварианты подобия выражаются комплексами величин, полученными преобразованием дифференциальных уравнений, описывающих процесс, то их называют критериями подобия. Как будет видно из дальнейшего, критерии подобия всегда имеют физический смысл, являясь мерами соотношения между какими-то двумя эффектами (силами и т. п.), существенными для рассматриваемого процесса. Критерии подобия обладают всеми свойствами инвариантов: они безразмерны, могут изменять свое значение от точки к точке данной системы, но для сходственных точек подобных систем не зависят от относительных размеров натуры и модели. В силу безразмерности числовые значения критериев подобия, как и констант и инвариантов подобия, не зависят от применяемой системы единиц. Критерии подобия могут быть получены для любого процесса, если известны аналитические зависимости между характеризующими его величинами – дифференциальные уравнения, описывающие процесс. Вместе с тем следует отметить, что один и тот же процесс, которому соответствует определенное дифференциальное уравнение, может быть интегрально описан при использовании различных систем критериев. Безразмерные симплексы или комплексы величин, в частности критерии подобия, называют также обобщенными переменными. Основные положения теории подобия обобщаются теоремами подобия, приводимыми ниже. Эти теоремы лежат в основе практического применения теории подобия. Первая теорема подобия была сформулирована Ньютоном. Согласно этой теореме, при подобии систем всегда могут быть найдены такие безразмерные комплексы величин, которые для сходственных точек данных систем одинаковы, т. е. подобные явления характеризуются численно равными критериями подобия. Первая теорема подобия указывает, какие величины следует измерять при проведении опытов, результаты которых требуется обобщить: надо измерять те величины, которые входят в критерии подобия. Вторая теорема подобия была доказана Бэкингемом, Федерманом и Афанасьевой-Эренфест. Согласно этой теореме, решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде зависимости между безразмерными комплексами этих величин, т. е. между критериями подобия. |
