Гидрогазодинамика. nchti_Рузанова_Гидрогазодинамика_уч_пособие (1). Гидрогазодинамика учебное пособие
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
12. Уравнение Бернулли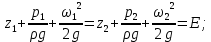 (56) (56)ω – средняя скорость потока; р – гидростатическое давление; z – геометрический напор, т.е. удельная потенциальная энергия геометрического положения потока жидкости в данном сечении(м); 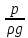 – статический или пьезометрический напор, т.е. удельная потенциальная энергия гидростатического давления жидкости в данном сечении (м); – статический или пьезометрический напор, т.е. удельная потенциальная энергия гидростатического давления жидкости в данном сечении (м);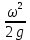 – скоростной или динамический напор, т.е. удельная кинетическая энергия потока жидкости в данном сечении (м); – скоростной или динамический напор, т.е. удельная кинетическая энергия потока жидкости в данном сечении (м);E – полный гидродинамический напор или полная удельная механическая энергия потока жидкости в данном сечении. В любых поперечных сечениях стационарного потока идеальной (невязкой) жидкости полный гидродинамический напор постоянен, т.е. полная удельная механическая энергия потока жидкости постоянна по длине труба. Уравнение Бернулли выражает энергетический баланс потока и является частным случаем закона сохранения энергии. Напор – удельная весовая механическая энергия потока жидкости. Уравнение Бернулли можно записать иначе, если умножить обе его части на величину 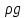 : :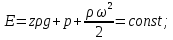 (57) (57)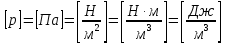 р – механическая энергия единицы объема жидкости (потока). Уравнение Бернулли можно применять для реальной (вязкой) жидкости: 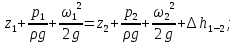 (58) (58)∆h1-2 – потеря напора потока на участке трубы между сечениями 1-1 и 2-2. Потерянный напор расходуется на преодоление гидравлического сопротивления трубопровода. Последнее складывается из потерь на трение между слоями жидкости, между жидкостью и стенками трубы, а так же в местных сопротивлениях (резкий поворот трубы, внезапное изменение сечения потока, запорно-регулирующая арматура и т.д.). При этом часть удельной потенциальной энергии жидкости превращается в тепловую энергию и рассеивается в окружающем пространстве. Рассмотрим диаграмму Бернулли: 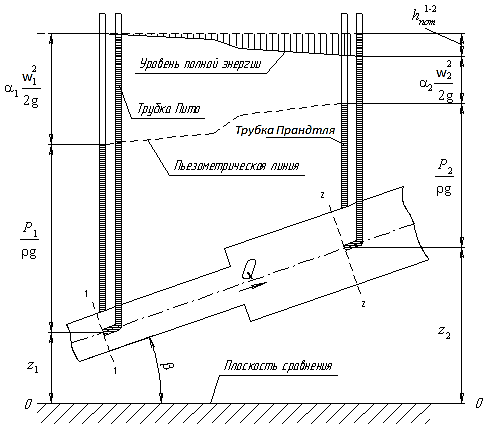 Рис.23. Диаграмма Бернулли Трубки Пито и Прандтля называют пьезометрическими. Иногда еще используют комбинированную трубку Пито-Прандтля. Высота столбика жидкости в трубке Прандтля равна пьезометрическому напору: 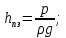 (59) (59)Высота столбика жидкости в трубке Пито равна сумме статического и скоростного напоров: 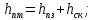 (60) (60)Отсюда, разность уровней столбиков жидкости в трубках Пито и Прандтля равна скоростному напору: 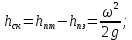 (61) (61)Если нижние концы трубок Пито и Прандтля находятся строго на оси трубы, то: 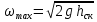 , таким образом, локальную скорость на оси трубы можно определить по показателям трубок Пито-Прандтля. , таким образом, локальную скорость на оси трубы можно определить по показателям трубок Пито-Прандтля.Имеется важное для практики следствие из уравнения Бернулли: при сужении потока часть удельной потенциальной энергии давления переходит в удельную кинетическую энергию потока жидкости, т.е. давление понижается, а скорость увеличивается; при расширении потока – все наоборот: скорость понижается, давление увеличивается. Примеры практического применения уравнения Бернулли – насосы, компрессоры, дроссельные расходомеры, подъемная сила крыла самолета, птицы, эффект Магнуса и т.д. 13. Пути исследования процессов химической технологии. Сущность теории подобия и моделирования процессовИзучение процессов с целью получения уравнений, необходимых для их анализа и расчета, можно проводить чисто теоретически. Этот наиболее желательный путь исследования сводится к составлению (на основе самых общих законов физики и химии) и решению математических зависимостей, чаще всего дифференциальных уравнений, полностью описывающих процесс. Примером важных для практики расчетных зависимостей, полученных решением соответствующих дифференциальных уравнений, являются рассмотренные выше основное уравнение гидростатики и уравнение Бернулли. Дифференциальные уравнения описывают целый класс однородных по своей сущности явлений, и для выделения из него конкретного явления необходимо ограничивать указанные уравнения дополнительными условиями (условиями однозначности). Условия однозначности включают: геометрические формы и размеры системы, т. е. аппаратура, в которой протекает процесс; существенные для данного процесса физические константы участвующих в нем веществ; начальные условия, к числу которых относятся начальная скорость, начальная температура, начальная концентрация и т. п.; граничные условия, характеризующие состояние на границах системы, например, равенство нулю скорости жидкости у стенок трубы, и т. д. Таким образом, дифференциальные уравнения должны решаться в совокупности с условиями однозначности в устанавливаемых последними пределах. Однако многие процессы химической технологии характеризуются большим числом переменных и настолько сложны, что зачастую удается дать лишь математическую формулировку задачи и установить условия однозначности. Полученные же дифференциальные уравнения не могут быть решены известными в математике методами. Теория подобия является учением о методах научного обобщения эксперимента. Она указывает, как надо ставить опыты и как обрабатывать их результаты, чтобы при проведении небольшого числа экспериментов иметь возможность обобщать опытные данные, получая единые уравнения для всех подобных явлений. Применение теории подобия часто позволяет вместо дорогостоящих трудоемких опытов на промышленной аппаратуре выполнять исследования на моделях значительно меньшего размера; помимо этого, опыты можно проводить не с рабочими (часто вредными и опасными) веществами и не в жестких (высокие температуры, сильно агрессивные среды) условиях реального производственного процесса, а с другими (модельными) веществами в условиях, отличающихся от промышленных. |
