Гидрогазодинамика. nchti_Рузанова_Гидрогазодинамика_уч_пособие (1). Гидрогазодинамика учебное пособие
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
6. Основное уравнение гидростатикиИз уравнения (31) следует, что давление в покоящейся жидкости изменяется только по вертикали, оставаясь одинаковым во всех точках любой горизонтальной плоскости, так как изменение давлений вдоль осей x и y равны нулю. Так как 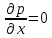 и и 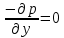 , то , то 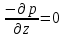 можно заменить на можно заменить на 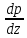 . .Тогда: 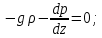 (32) (32)Отсюда: 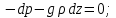 (33) (33)Разделив левую и правую части выражения (33) на 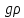 и переменив знаки, получим: и переменив знаки, получим: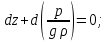 (34) (34)или 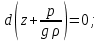 (35) (35)Отсюда после интегрирования получим: 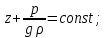 (36) (36)Для двух произвольных горизонтальных плоскостей 1 и 2 уравнение (35) выражают в форме 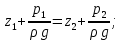 (37) (37)Уравнение (37) является основным уравнением гидростатики. z1 и z2 – высоты расположения двух точек внутри покоящейся однородной капельной жидкости над произвольно выбранной горизонтальной плоскостью отсчета (плоскостью сравнения), а p1 и p2 – гидростатические давления в этих точках. В гидростатике изучают законы равновесия жидкостей, неподвижных относительно стенок сосуда, хотя сам сосуд может двигаться (например, железнодорожная цистерна). 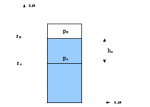 Рис.11. Иллюстрация основного уравнения гидростатики Пусть p0 – давление на свободной поверхности слоя неподвижной жидкости, т.е. на уровне z0; pх – давление на глубине hx, т.е. на уровне zx. Тогда 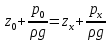 – основное уравнение гидростатики. – основное уравнение гидростатики.z – геометрический напор, т.е. удельная потенциальная энергия положения жидкости на данном уровне (энергия геометрического положения); 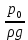 – статический или пьезометрический напор, т.е. удельная потенциальная энергия гидростатического давления жидкости на данном уровне; – статический или пьезометрический напор, т.е. удельная потенциальная энергия гидростатического давления жидкости на данном уровне;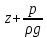 – полная удельная потенциальная энергия жидкости на данном уровне. – полная удельная потенциальная энергия жидкости на данном уровне. При погружении в слой неподвижной жидкости геометрический напор падает, а статический напор растет. При этом полная удельная потенциальная энергия остается постоянной. Из основного уравнения гидростатики можно получить: 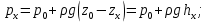 (38) (38)Выражение (36) – закон Паскаля, который говорит, что гидростатическое давление в любой точке объема неподвижной жидкости равно давлению на свободной поверхности данного слоя жидкости плюс вес столбика жидкости единичного сечения над данной точкой. Следствия из закона Паскаля: давление в любой точке слоя неподвижной жидкости на одинаковой глубине одно и то же; при изменении давления на свободной поверхности слоя неподвижной жидкости на величину ∆р давление в любой точке этого слоя изменится на ту же величину ∆р, т.е. давление передается во все точки неподвижного слоя жидкости одинаково. Примеры практического применения основного уравнения гидростатики – гидроаккумуляторы, гидравлический пресс, сообщающиеся сосуды и т.п. 7. Сила давления жидкости на плоскую стенку. Центр давленияСила полного гидростатического давления на плоскую стенку равна гидростатическому давлению в центре тяжести смоченной стенки, умноженному на ее смоченную поверхность. 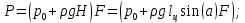 (39) (39)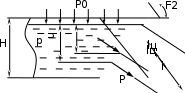 Рис.12. Давление на плоскую стенку Последняя формула справедлива также для вертикальной стенки (α = 90˚, hц = lц). В случае наклонной стенки силу Ρ можно рассмотреть как сумму двух сил: 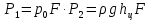 . Сила Ρ1 представляет собой результирующую равномерной нагрузки и приложена в центре тяжести площади F. А сила Ρ2 – равнодействующая сил избыточного давления, распределенных по площади F неравномерно, т.к. с увеличением глубины погружения давление растет. Следовательно, точка приложения этой силы смещена от центра тяжести в сторону большей глубины. . Сила Ρ1 представляет собой результирующую равномерной нагрузки и приложена в центре тяжести площади F. А сила Ρ2 – равнодействующая сил избыточного давления, распределенных по площади F неравномерно, т.к. с увеличением глубины погружения давление растет. Следовательно, точка приложения этой силы смещена от центра тяжести в сторону большей глубины.Центр давления – точка приложения сил избыточного давления жидкости на стенку. Гидростатический парадокс: сила давления жидкости на горизонтальное дно сосудов не зависит от их формы: 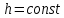 ; ; 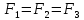 ; ; 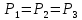 .F – площадь дна. При данной плотности сила давления на горизонтальное дно сосуда определяется лишь высотой столба жидкости H и площадью F дна сосуда: .F – площадь дна. При данной плотности сила давления на горизонтальное дно сосуда определяется лишь высотой столба жидкости H и площадью F дна сосуда: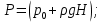 (40) (40)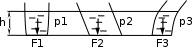 Рис.13. Гидростатический парадокс Практическое применение основного уравнения гидростатики – гидростатические машины, сообщающиеся сосуды. Например, в ХП используются гидравлические прессы.  Рис.14. Гидропресс Поршень 2 передаст силу давления R1 во столько раз большую, чем R2, во сколько раз сечение цилиндра 2 больше, чем сечение цилиндра 1. 1, 2 – поршни; 3 – прессуемый материал; 4 – неподвижная плита. Сила давления на поршень 1 и 2: 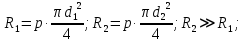 (41) (41) |
