Гидрогазодинамика. nchti_Рузанова_Гидрогазодинамика_уч_пособие (1). Гидрогазодинамика учебное пособие
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
17. Тепловое подобное преобразование уравнений Навье-Стокса. Основные критерии гидродинамического подобияВыше уже отмечалось, что дифференциальные уравнения Навье-Стокса невозможно решить практически для большинства важных случаев. Теория подобия позволяет преобразовать уравнения Навье-Стокcа и получить из них некоторую общую функциональную зависимость между критериями подобия, характеризующих силы, действующие при движении вязкой жидкости. Перепишем уравнение Навье-Стокса для капельной жидкости в развернутом виде для одной из осей – вертикальной оси z: 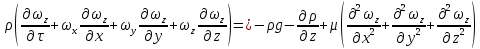 Для подобного преобразования этого уравнения воспользуемся ранее сформулированным правилом: критерии подобия можно получить путем деления одной части дифференциального уравнения на другую и последующего отбрасывания знаков математических операторов. Если движение жидкости установившееся, то ее скорость не зависит от времени, т. е. член 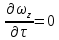 . При этом, заменяя в левой части уравнения, характеризующей силу инерции, дифференциалы конечными величинами, находим: . При этом, заменяя в левой части уравнения, характеризующей силу инерции, дифференциалы конечными величинами, находим: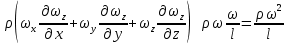 где l – определяющий линейный размер. В правой части уравнения член, отражающий действие силы тяжести, равен ρg. Член 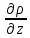 , характеризующий действие силы давления, можно заменить отношением , характеризующий действие силы давления, можно заменить отношением 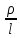 , т. е. , т. е. 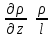 Наконец, последнее слагаемое правой части, отражающее действие силы трения: Наконец, последнее слагаемое правой части, отражающее действие силы трения: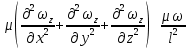 Разделим члены одной части уравнения на члены другой его части и найдем таким образом выражения, характеризующие соотношения между соответствующими силами и силой инерции, или, иначе говоря, выразим эти силы в относительных единицах, приняв за масштаб силу инерции. В результате получим безразмерные соотношения величин – критерии подобия. Выражение, характеризующее отношение силы тяжести к силе инерции, имеет вид 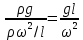 Безразмерный комплекс 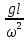 представляет собой критерий Фруда и обозначается через Fr. Чтобы избежать чисел меньше единицы, предпочитают пользоваться обратным выражением, и, таким образом, критерием Фруда обычно называют величину представляет собой критерий Фруда и обозначается через Fr. Чтобы избежать чисел меньше единицы, предпочитают пользоваться обратным выражением, и, таким образом, критерием Фруда обычно называют величину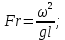 (79) (79)Критерий Фруда отражает влияние сил тяжести или собственного веса на движение жидкости. В виде выражения он является мерой отношения силы инерции к силе тяжести в подобных потоках. Соотношение между силами давления и инерции может быть охарактеризовано выражением: 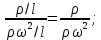 (80) (80)Полученный комплекс 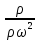 называют критерием Эйлера и обозначают через Eu. Обычно ему придают несколько иной вид, вводя в него вместо абсолютного давления ρ разность давлений Δρ между какими-либо двумя точками жидкости: называют критерием Эйлера и обозначают через Eu. Обычно ему придают несколько иной вид, вводя в него вместо абсолютного давления ρ разность давлений Δρ между какими-либо двумя точками жидкости: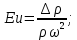 (81) (81)Критерий Эйлера отражает влияние перепада гидростатического давления на движение жидкости. Он характеризует отношение изменения силы гидростатического давления к силе инерции в подобных потоках. Найдем выражение, являющейся мерой отношения силы трения к силе инерции, приняв за критерий подобия (для того чтобы избежать чисел, меньших единицы) обратное отношение: 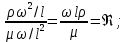 (82) (82)Полученный безразмерный комплекс величин 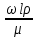 называется, как известно, критерием Рейнольдса. называется, как известно, критерием Рейнольдса.Таким образом, критерий Рейнольдса отражает влияние силы трения на движение жидкости. Он характеризует отношение инерционных сил к силам трения в подобных потоках. Величина l в критерии Re, как и в других критериях подобия, представляет собой определяющий линейный размер. При движении жидкости через трубопроводы или аппараты за такой размер принимается их диаметр d, а в случае некруглого сечения потока – эквивалентный диаметр dэ. При неустановившемся движении жидкости в уравнении Навье-Стокса 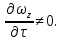 Заменив член, отражающий влияние нестационарности движения Заменив член, отражающий влияние нестационарности движения 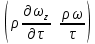 , охарактеризуем соотношение между силой инерции и этой величиной: , охарактеризуем соотношение между силой инерции и этой величиной: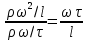 (83) (83)Безразмерный комплекс 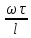 называется критерием гомохронности и обозначается через Но. Следовательно называется критерием гомохронности и обозначается через Но. Следовательно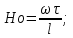 (84) (84)Критерий гомохронности учитывает неустановившийся характер движения в подобных потоках. Во всех сходственных точках движущихся подобно жидкостей
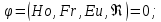 (85) (85)В ряде случаев зависимость должна быть дополнена симплексами геометрического подобия. При движении жидкости через трубы или каналы таким симплексом является отношение длины l трубы к ее диаметру d или эквивалентному диаметру dэ. Тогда критериальное уравнение принимает вид: 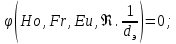 (86) (86)При наиболее важной для практики формулировке задачи все входящие в уравнение критерии, кроме критерия Эйлера, служат определяющими, так как они составлены исключительно из величин, выражающих условия однозначности. В критерий же Эйлера входит величина Δρ, значение которой при движении жидкости по, трубе полностью обусловливается формой трубы (отношением 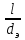 ), физическими свойствами жидкости (µ, ρ) и распределением скоростей у входа в трубу и у ее стенок (начальные и граничные условия). Поэтому, согласно третьей теореме подобия, для подобия необходимо и достаточно соблюдение равенства значений Но, Fr, Re и ), физическими свойствами жидкости (µ, ρ) и распределением скоростей у входа в трубу и у ее стенок (начальные и граничные условия). Поэтому, согласно третьей теореме подобия, для подобия необходимо и достаточно соблюдение равенства значений Но, Fr, Re и 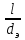 . Следствием выполнения этих условий будет также равенство значений определяемого критерия Eu в сходственных точках подобных потоков. Поэтому уравнение представляют как . Следствием выполнения этих условий будет также равенство значений определяемого критерия Eu в сходственных точках подобных потоков. Поэтому уравнение представляют как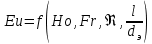 ; (87) ; (87)Зависимости называют обобщенным, или критериальным, уравнением гидродинамики. Функцию (85) наиболее часто аппроксимируют степенной зависимостью, т. е. придают этой функции вид 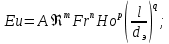 (88) (88)или после подстановки соответствующих безразмерных комплексов величин 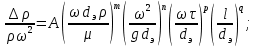 (89) (89)Путем обработки опытных данных, полученных на моделях, находят числовые значения коэффициента А и показателей степеней m, n, p, qпри соответствующих критериях. Из полученного уравнения обычно определяют величину Δρ, входящую в критерий Eu. В частности, при движении жидкости через трубопроводы и аппараты так находится потеря давления (напора). Если движение жидкости является установившимся, то критерий гомохронности может быть исключен из уравнений Следовательно, для установившегося движения обобщенное уравнение гидродинамики имеет вид: 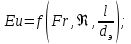 (90) (90)или в более общей форме 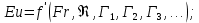 (91) (91)где Г1, Г2, Г3, ... – симплексы геометрического подобия. |
