Гидрогазодинамика. nchti_Рузанова_Гидрогазодинамика_уч_пособие (1). Гидрогазодинамика учебное пособие
 Скачать 1.56 Mb. Скачать 1.56 Mb.
|
15. Принципы аналогии. Сущность математического моделированияДля весьма сложных химико-технологических процессов, проводимых, например, в химических реакторах с катализаторами, подобное преобразование дифференциальных уравнений приводит к выводу зависимостей между большим числом критериев подобия. Надежное моделирование таких процессов на малой опытной установке с последующим распространением полученных данных на производственные условия, т. е. применение изложенных выше принципов физического моделирования, практически невозможно. В связи с этим исследование указанных процессов приходится проводить последовательно на ряде опытных установок, постепенно приближающихся по масштабу к промышленным установкам, что сопряжено с большими затратами времени и средств. Значительно более экономично и эффективно изучение характеристик сложных явлений на моделях, процессы в которых имеют иную физическую сущность, чем процессы в натуре. В последние годы такой метод все шире применяется в инженерной практике. В основе данного метода лежит свойство изоморфизма дифференциальных уравнений, являющееся отражением единства законов природы. Это свойство заключается в том, что с помощью системы однотипных дифференциальных уравнений можно описывать различные по своей физической сущности явления. Например, аналогичные уравнения применимы для описания полей скоростей, температур, концентраций и т. д. Таким образом, существует аналогия и между физически разнородными процессами. Подобие физически однородных процессов можно рассматривать как частный случай аналогии. Аналогия существует между электрическими, тепловыми и массообменными процессами, а также между гидродинамическими, тепловыми и массообменными процессами. Поэтому при исследовании тепловых, массообменных или гидродинамических процессов можно использовать более простые и в каком-либо отношении более удобные, чем натура, модели, в которых протекает совсем другой физический процесс. Единственное условие применимости такого способа исследования заключается в том, что оба процесса должны описываться одинаковыми по виду дифференциальными уравнениями. Так, например, электротепловая аналогия может быть применена путем использования описанного выше метода электролитической ванны для исследования полей температур в реакционных аппаратах. 16. Основные принципы метода анализа размерностейМногие процессы химической технологии зависят от такого большого числа различных факторов, что для них не удается получить полного математического описания; можно лишь в самом общем виде представить зависимость между различными переменными, влияющих на протекание процесса. Если, например, согласно практическим данным, некоторая величина а зависит от параметров β, γ, δ, и θ, то общий вид зависимости между данными величинами имеет вид: 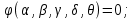 (75) (75)или 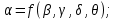 (76) (76)Для отыскания конкретного вида этой функциональной зависимости, т. е. для нахождения расчетного уравнения, может быть применен метод анализа размерностей. В основу метода положена π-теорема Бэкингема, согласно которой общую функциональную зависимость, связывающую между собой n переменных величин при m основных единицах их измерения, можно представить в виде зависимости между (n – m) безразмерными комплексами этих величин, а при наличии подобия – в виде связи между (n – m) критериями подобия. Так, например, если рассматриваемое явление описывается в общем виде соотношением, связывающим пять каких-то физических величин, и если эти величины выражаются посредством трех основных единиц измерения, то n = 5 и m = 3. Следовательно, (n – m) = 2, и указанная функциональная зависимость может быть представлена в виде функции между некоторыми двумя безразмерными комплексами π1 и π2: 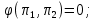 (77) (77)или 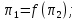 (78) (78)Для пользования методом анализа размерностей необходимо заранее знать, какие переменные должны входить в зависимость общего вида. Если при составлении такой исходной зависимости не учесть тех или иных параметров, которые существенно влияют на процесс, то это может привести к серьезным ошибкам при получении конечного расчетного уравнения, что является недостатком метода анализа размерностей. При отсутствии надежных исходных данных, вытекающих из физической сущности процесса, в случае применения данного метода для их выяснения нередко приходится использовать инженерную интуицию. Рассмотрим применение методов теории подобия и анализа размерностей к гидродинамическим процессам. |
