Главная страница
Навигация по странице:

  • ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТАимени адмирала С.О. МАКАРОВА Институт водного транспорта

  • Анализ статистической однородности технологических процессов в строительстве

  • Санкт-Петербург2021 г. Анализ

  • Результаты обработки данных для построения гистограммы

  • Обработка данных для расчета критерия согласия χ2

    		•

    Анализ статистической однородности технологических процессов в строительстве. ПР№3 Пашнева ЮМ Метрология. Государственный университет морского и речного флота имени адмирала С. О. Макарова институт водного транспорта Дисциплина Основы метрологии


    Скачать 75.46 Kb.
    НазваниеГосударственный университет морского и речного флота имени адмирала С. О. Макарова институт водного транспорта Дисциплина Основы метрологии
    АнкорАнализ статистической однородности технологических процессов в строительстве
    Дата23.02.2022
    Размер75.46 Kb.
    Формат файлаdocx
    Имя файлаПР№3 Пашнева ЮМ Метрология.docx
    ТипАнализ
    #370969

    Федеральное агентство морского и речного транспорта

    Федеральное государственное бюджетное образовательное учреждение высшего образования

    ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТА
    имени адмирала С.О. МАКАРОВА



    Институт водного транспорта


    Дисциплина «Основы метрологии»

    Анализ статистической однородности технологических процессов в строительстве.

    Вариант № 16

    Выполнил: ст. гр. ГТ-42 Пашнева Ю.М.

    Проверил: Ксенофонтов Ю.Г.


    Санкт-Петербург
    2021 г.

    Анализ статистической однородности технологических процессов в строительстве

    Описаниеработы

    Цели работы — освоение общепринятой проверки статистической однородности технологических процессов в строительстве при производстве строительных элементов их установке и монтаже.

    Содержаниеработы. Каждый студент выполняет следующее:

      • получает от преподавателя индивидуальный вариант с результатами 50-ти кратного измерения какого-либо геометрического параметра строительного элемента;

      • строит гистограмму распределения результатов и теоретическую кривую плотности нормального распределения;

      • рассчитывает критерий согласия χ2 и делает вывод о соответствии распределения экспериментальных данных нормальному распределению;

      • определяет погрешность измерений;

      • определяет точность технологического процесса по шкале стандартных классов точности.

    Таблица1

    Расчет среднего арифметического и оценки СКО


    №
    Результаты расчёта по исходной выборке






    хi, мм
    xi-x, мм
    (xi -x)2






    1
    2
    3
    4






    1
    600
    -2,1
    4,41






    2
    600
    -2,1
    4,41






    3
    603
    0,9
    0,81






    4
    604
    1,9
    3,61






    5
    602
    -0,1
    0,01






    6
    603
    0,9
    0,81






    7
    603
    0,9
    0,81






    8
    603
    0,9
    0,81






    9
    602
    -0,1
    0,01






    10
    601
    -1,1
    1,21






    11
    599
    -3,1
    9,61






    12
    603
    0,9
    0,81






    13
    603
    0,9
    0,81






    14
    603
    0,9
    0,81






    15
    606
    3,9
    15,21






    16
    606
    3,9
    15,21






    17
    607
    4,9
    24,01






    18
    608
    5,9
    34,81






    19
    609
    6,9
    47,61






    20
    613
    10,9
    118,81






    21
    606
    3,9
    15,21






    22
    606
    3,9
    15,21






    23
    607
    4,9
    24,01






    24
    607
    4,9
    24,01






    25
    607
    4,9
    24,01






    26
    605
    2,9
    8,41






    27
    599
    -3,1
    9,61






    28
    599
    -3,1
    9,61






    29
    600
    -2,1
    4,41






    30
    594
    -8,1
    65,61






    31
    593
    -9,1
    82,81






    32
    597
    -5,1
    26,01






    33
    598
    -4,1
    16,81






    34
    598
    -4,1
    16,81






    35
    598
    -4,1
    16,81






    36
    601
    -1,1
    1,21






    37
    601
    -1,1
    1,21






    38
    601
    -1,1
    1,21






    39
    598
    -4,1
    16,81






    40
    598
    -4,1
    16,81






    41
    604
    1,9
    3,61






    42
    604
    1,9
    3,61






    43
    600
    -2,1
    4,41






    44
    602
    -0,1
    0,01






    45
    600
    -2,1
    4,41






    46
    598
    -4,1
    16,81






    47
    598
    -4,1
    16,81






    48
    602
    -0,1
    0,01






    49
    604
    1,9
    3,61






    50
    602
    -0,1
    0,01






    Сумма
    30105



    734,5






    Таблица 2

    Результаты обработки данных для построения гистограммы

    №
    Границы интервала
    Число результатов n попавших в интервал
    Частость
    Эмирическая плотность вероятности

    нижняя
    верхняя

    1
    593
    596,0
    2
    0,04
    0,0132

    2
    595,8
    598,9
    8
    0,16
    0,0528

    3
    598,7
    601,7
    12
    0,24
    0,0792

    4
    601,5
    604,5
    16
    0,32
    0,1056

    5
    604,3
    607,3
    9
    0,18
    0,0594

    6
    607,1
    610,2
    2
    0,04
    0,0132

    7
    610,0
    613
    1
    0,02
    0,0066

    Таблица3

    Обработка данных для построения


    теоретической кривой нормального распределения

    №
    Границы интервала
    ni
    viн
    viв
    F(viн)
    F(viв)
    Pi
    pi



    нижняя
    верхняя



    1
    593,0
    596,0
    2
    -2,4
    -1,6
    0,0060
    0,0465
    0,0405
    0,0134

    2
    595,8
    598,9
    8
    -1,6
    -0,8
    0,0465
    0,1894
    0,1429
    0,0472

    3
    598,7
    601,7
    12
    -0,9
    -0,1
    0,1635
    0,4286
    0,2651
    0,0875

    4
    601,5
    604,5
    16
    -0,2
    0,6
    0,3897
    0,7257
    0,3360
    0,1109

    5
    604,3
    607,3
    9
    0,6
    1,4
    0,7257
    0,9192
    0,1935
    0,0639

    6
    607,1
    610,2
    2
    1,3
    2,1
    0,9032
    0,9821
    0,0789
    0,0260

    7
    610,0
    613,0
    1
    2,0
    2,8
    0,9773
    0,9974
    0,0201
    0,0066



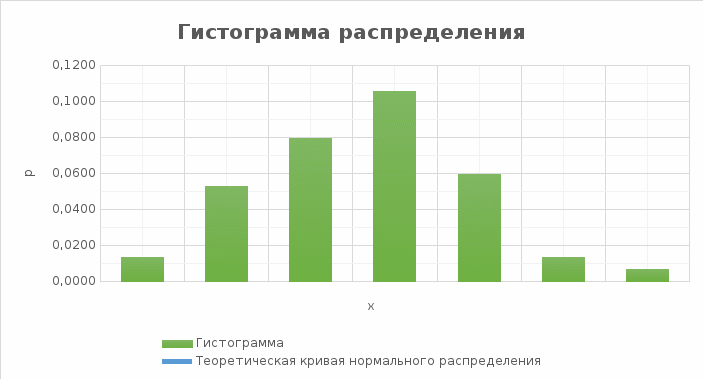    Рис. 1. Результаты построения гистограммы и теоретического (нормального) распределения

    Таблица 4

    Обработка данных для расчета критерия согласия χ2

    № интервала
    Границы интервала
    ni
    Pi
    nPi
     Xi2

    xн
    xв

    1
    593,0
    596,0
    2
    11
    0,0405
    2,025
    9,17
    0,365201745

    2
    595,8
    598,9
    8
    0,1429
    7,145

    3
    598,7
    601,7
    12
    12
    0,2651
    13,255
    0,118824972

    4
    601,5
    604,5
    16
    16
    0,3360
    16,8
    0,038095238

    5
    604,3
    607,3
    9
    12
    0,1935
    9,675
    14,625
    0,471153846

    6
    607,1
    610,2
    2
    0,0789
    3,945

    7
    610,0
    613,0
    1
    0,0201
    1,005






















    сумма
    0,9933


    Найдем по таблице Приложения 3 табличные значения χ2н и χ2в для числа степеней свободы k = m – 3 = 4 – 3 = 1 и доверительной вероятности 0,90, т. е. примем для верхнего значения χ2н уровень значимости 5 %, а для нижнего χ2в — 95 %:

    χ2в = 5,991 и χ2н = 0,103

    Так как χ2экс= 0,9933, то ­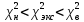 . Это значит, что гипотезао нормальном законе распределения погрешности измерений согласуется с экспериментальными данными.

    Произведем оценку доверительного интервала результата измерения x граней колонн для доверительной вероятности P = 0,95.

    При нормальном распределении измеряемой величины доверительный интервал оценивают в виде с использованием распределения Стьюдента: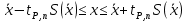



    СКО среднего арифметического, определяется по формуле: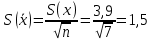



    Квантиль распределения Стьюдента выберем по Приложению 4:

    при числе измерений n = 50 и доверительной вероятности P = 0,95 коэффициент Стьюдента tP, n = 1,96. Таким образом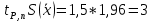

    Окончательно доверительный интервал запишем в виде: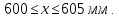



    Определим класс точности технологического процесса в следующей последовательности.

    Cделаем оценку ширины полосы разброса 2tS(x) результатов измерений размера граней колонн: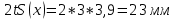

    ,
    где S(x) — СКО, рассчитанное по формуле (2.2) с использованием значения суммы для столбца 6 в табл. 2.5, и равное 3,9;

    t — квантильный коэффициент нормального распределения, равный

    3,0 для приемочного уровня дефектности 0,25 %, т. е. доверительной вероятности P = 99,73 % (см. табл. 1.9).

    По табл. 1.5 определим, что размер 392 мм попадает в диапазон от 250

    до 500 мм. Для интервала размеров 250…500 мм ближайшее к значению 23 значение допуска равно 20 и соответствует 8 классу точности.

    Определим по формуле запас точности, обеспечиваемый технологическим процессом: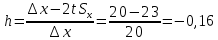



    Если h < –0,14, то процесс относится к более низкому классу точно- сти, т. е. классу, соответствующему меньшей точности.

    написать администратору сайта