2 вариант. Задача 21 Коэффициент линейной корреляции определяется формулой
 Скачать 152.5 Kb.
|
|
Задача 21 Коэффициент линейной корреляции определяется формулой:  , где  ,  ,  , ,  .Получим  .Напишем уравнения линейной регрессии  на  :  ,получим  или  . на :  , получим  или  .Ответ.  , , .Задача 12 Так как случайные величины 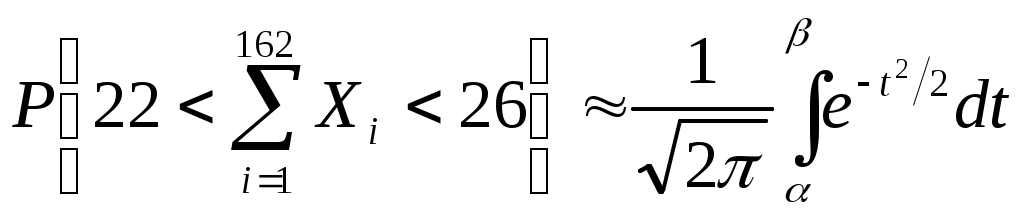 одина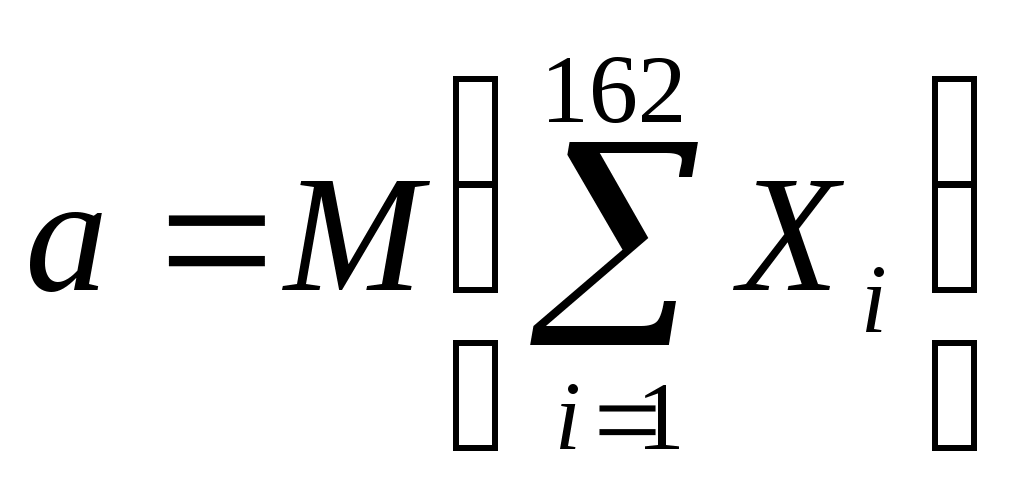ково распределены, то их сумма стремится к нормальному распределению. Следовательно  и  ,где  ,  .Из того, что распределены одинаково, следует, что их числовые характеристики равны, т.е. ,  .Для равномерно распределенной случайной величины имеем  ,  .Тогда 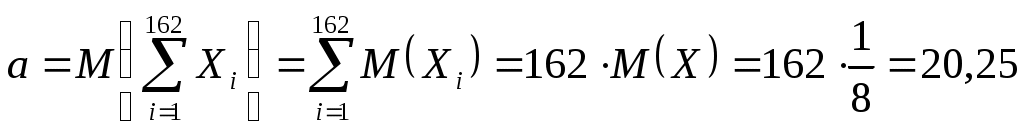 , 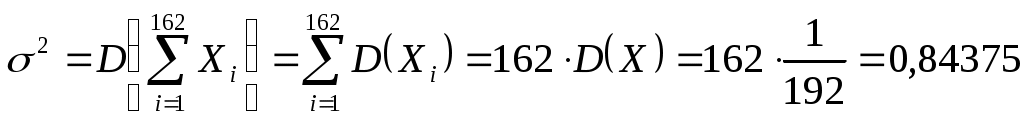.Получим  ,  .Тогда  .Ответ. 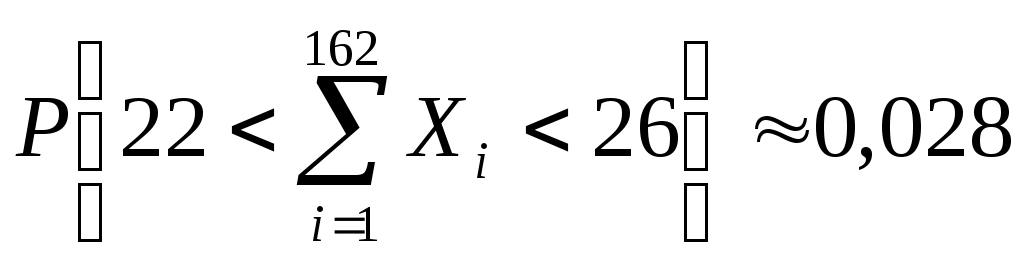 .Задача 11 По свойству плотности распределения вероятностей, имеем  .Тогда плотность распределения принимает вид 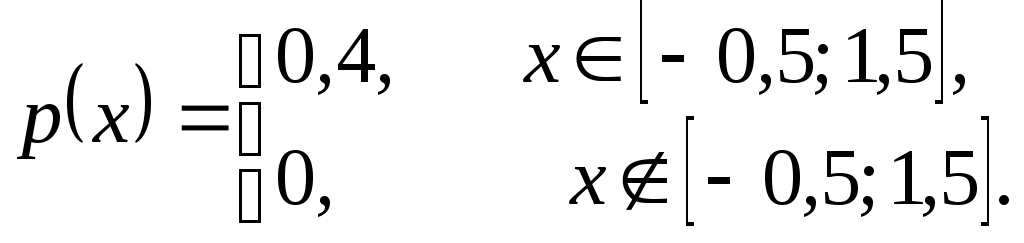 Функция распределения определяется формулой  .Если  , то  .Если  , то  .Если  , то  .Получим  Вычислим математическое ожидание  .Дисперсия случайной величины равна  .Найдем вероятность попадания случайной величины в заданный интервал  .Задача № 3 При бесконечном числе равновозможных элементарных исходов, представленных точками области на плоскости, вероятность события равна отношению площади множества элементарных исходов, благоприятствующих этому событию, к площади всего множества элементарных исходов. П  усть  и  – координаты первой и второй точек, выбранных на [0;1];  – множество всех элементарных исходов;  – множество элементарных исходов, благоприятствующих нашему событию. При этом  ;  .Тогда  , где  , а  (см. рис.).Получим  . |