схемы. Государственное бюджетное образовательное учреждение среднего профессионального образования
 Скачать 413.5 Kb. Скачать 413.5 Kb.
|
РОДОВИДОВЫЕРодовидовым является определение через род и видовое отличие. Структура родового определения: А=dfB и С, где А – определяемое понятие, В обозначает род, а С – видовое отличие Пример: Преступление есть предусмотренное уголовным законом общественно опасное деяние. Роль А играет понятие «преступление», В – «деяние», а С – «предусмотренное уголовным законом общественно опасное» НЕЯВНЫЕНеявное определение – это определение, которое не имеет формы равенства А=dfB, где А – определяемое понятие АКСИОМАТИЧЕСКИЕАксиоматическим является определение, в котором содержание понятий задается системой аксиом, в которых это понятие встречается. Пример: Содержание понятий «точка», «прямая», «плоскость» задается аксиомами геометрии КОНТЕКСТУАЛЬНЫЕКонтекстуальным является определение, в котором некоторый контекст использования определяемого понятия приравнивается к другому контексту, в который определяемое понятие не входит Пример: Операция возведенная в квадрат в арифметике определяется контекстуально а2 = а х а     ЯВНЫЕЯвным является определение, которое имеет форму равенства: А=dfB или может быть приведено к ней: а) понятие, которое определяется, - определяемое понятие (А), обозначается Dfd (дефиниендум); б) понятие, при помощи которого определяется другое понятие, - определяющее понятие (В), обозначается Dfn (дефиниенс); в) df – равно по определению  Схема 18. ПРАВИЛА ОПРЕДЕЛЕНИЯ Правило соразмерности В правильном определении объемы определяемого и определяющего понятий совпадают 2. Правило запрета круга Кругом в определении является логическая ошибка, заключающаяся в том, что понятие А определяется при помощи понятия В, а понятие В в свою очередь определяется при помощи понятия А.3. Правило неотрицательности Определение по возможности не должно содержать в определяющем понятии отрицательных признаков 4. Правило ясности Определение должно быть как можно более яснымСхема 19. ЛОГИЧЕСКИЕ ОПЕРАЦИИ С ПОНЯТИЯМИ (деление по видоизменению признака) Логическая операция, раскрывающая объем понятия, называется делением Пример: 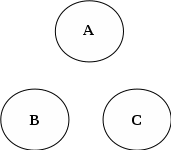      А – делимое понятие А – форма государственного устройства В, С – члены деления В – унитарная С – федеративная Схема 20. ЛОГИЧЕСКИЕ ОПЕРАЦИИ С ПОНЯТИЯМИ (дихотомическое деление) Пример:       А – делимое понятие А – современное государство В, не-В – члены деления В – демократическое не-В - недемократическое Схема 21. ПРАВИЛА ДЕЛЕНИЯ И ВОЗМОЖНЫЕ ОШИБКИ  Правило соразмерности Объединение объемов членов деления должно совпадать с объемом делимого понятия А – объем делимого понятия, В1, В2…Вn– все члены деления. Ошибки: Деление неполно, если среди членов деления не достает какого-либо вида предметов, выделяемого по данному признаку Деление обширно, если объем делимого понятия является частью объединения объемов членов деления Схема 22. СУЖДЕНИЕ    Схема 23. СТРУКТУРА СУЖДЕНИЯ 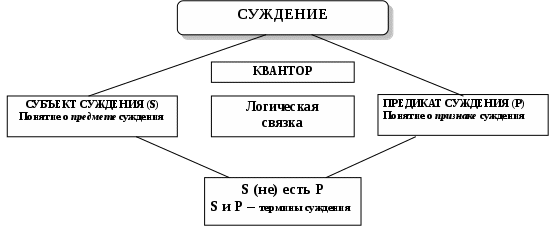 Схема 24. ВИДЫ ПРОСТЫХ СУЖДЕНИЙ  Схема 25. ДЕЛЕНИЕ СУЖДЕНИЙ ПО КАЧЕСТВУ И КОЛИЧЕСТВУ 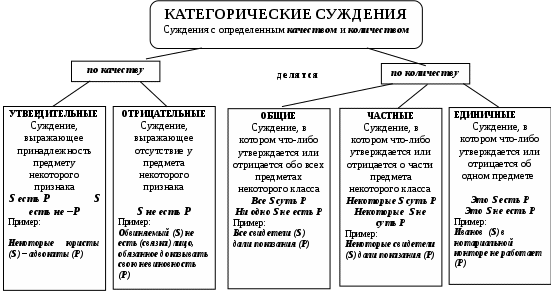 Схема 26. ВЫДЕЛЯЮЩИЕ И ИСКЛЮЧАЮЩИЕ СУЖДЕНИЯ  Схема 27. ОБЪЕДИНЕННАЯ КЛАССИФИКАЦИЯ СУЖДЕНИЙ ПО КОЛИЧЕСТВУ И КАЧЕСТВУ  Схема 28. РАСПРЕДЕЛЕННОСТЬ ТЕРМИНОВ В СУЖДЕНИЯХ
Субъект и предикат категорического суждения – термины суждения. Термин распределен, если он взят в полном объеме. Схема 29. ТАБЛИЦА РАСПРЕДЕЛЕННОСТИ ТЕРМИНОВ
Субъект распределен в общих (А и Е) и не распределен в частных суждениях (I и O). Предикат распределен в отрицательных (Е и О) и не распределен в утвердительных суждениях (А и I). В выделяющих суждениях предикат распределен. Обозначения: + - распределенность термина - - нераспределенность термина Схема 30. СЛОЖНЫЕ СУЖДЕНИЯ  Схема 31. СВОДНАЯ ТАБЛИЦА УСЛОВИЙ ИСТИННОСТИ СЛОЖНЫХ СУЖДЕНИЙ
Схема 32. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ СУЖДЕНИЯМИ (простые суждения) 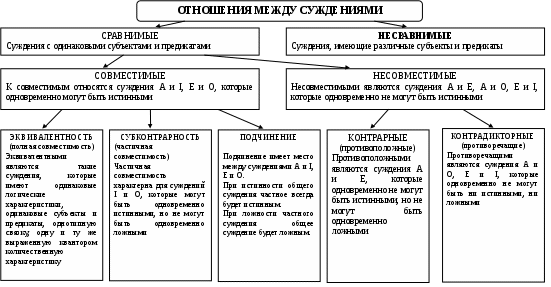 Схема 33. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ (логический квадрат) 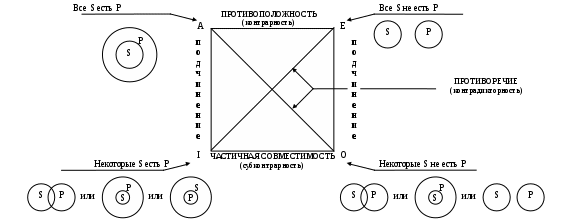 Логическому квадрату эквивалентна таблица 1, иллюстрирующая функционально-истинностные отношения между высказываниями вида A, E, I, O. Таблица 1
Из таблицы 1 высказывания А и О, а также E и I не могут быть одновременно ни истинными, ни ложными. Это означает: высказывание вида А контрадикторно высказыванию вида О (и, соответственно, E контрадикторно I). Из таблицы 1 высказывания А и Е не могут быть одновременно истинными, но могут быть одновременно ложными. В этом смысле всякое высказывание вида А контрарно соответствующему высказыванию вида Е. Аналогичным образом с помощью таблицы 1 легко понять отношение субконтрарности между высказываниями вида I, O и отношение подчинения между высказываниями вида A, I (а также вида Е, О). Схема 34. ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ СУЖДЕНИЯМИ (логический треугольник) 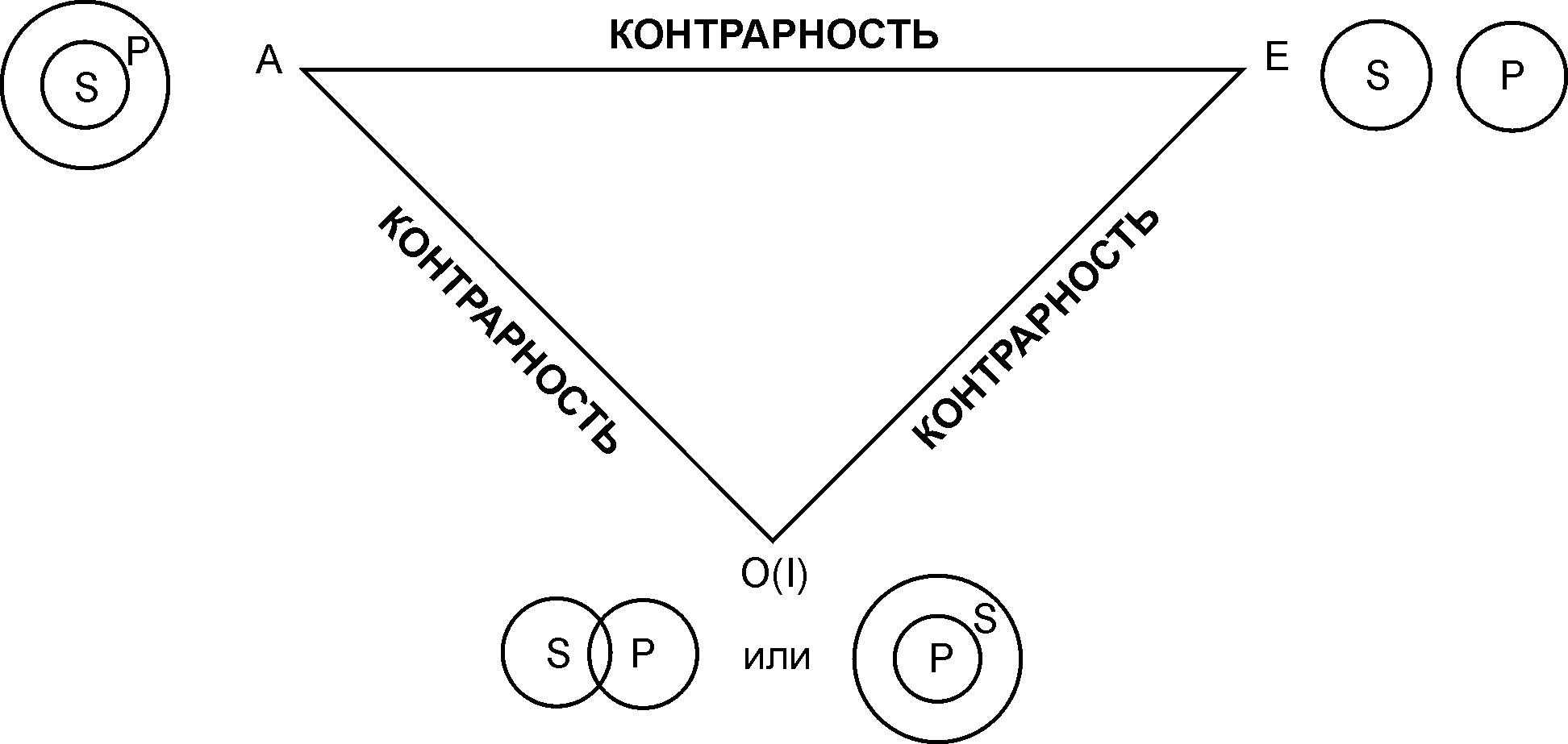 Примечание: При использовании логического квадрата учитывается следующее: слово «некоторые» понимается в широком смысле, как «некоторые, а может быть, и все». Если же слово «некоторые» понимается в узком смысле, как «только некоторые» («некоторые, но не все»), то в этом случае логический квадрат трансформируется в логический треугольник. Логический треугольник иллюстрирует то, что отношение контрарности более фундаментально, чем отношение субконтрарности и отношение подчинения. Таблица 2
Схема 35. ВОПРОСНО – ОТВЕТНАЯ ОСНОВА ПОСТРОЕНИЯ ДЕЛОВОГО РАЗГОВОРА (виды вопросов) Вопрос – это выраженная в вопросительном положении мысль, направленная на уточнение или дополнение знаний. 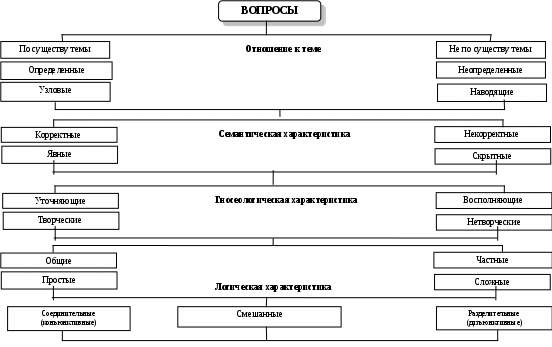 Схема 36. ВОПРОСНО – ОТВЕТНАЯ ОСНОВА ПОСТРОЕНИЯ ДЕЛОВОГО РАЗГОВОРА (виды ответов) Ответ – новое суждение, уточняющее или дополняющее в соответствии с поставленным вопросом прежнее знание. 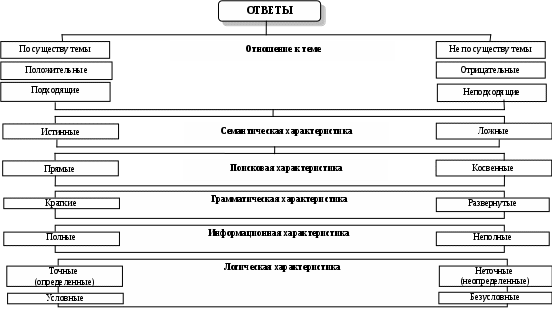 Схема 37. МОДАЛЬНОСТЬ СУЖДЕНИЙ (структура модальных суждений)  Схема 38. ВИДЫ МОДАЛЬНОСТЕЙ (алетическая модальность) 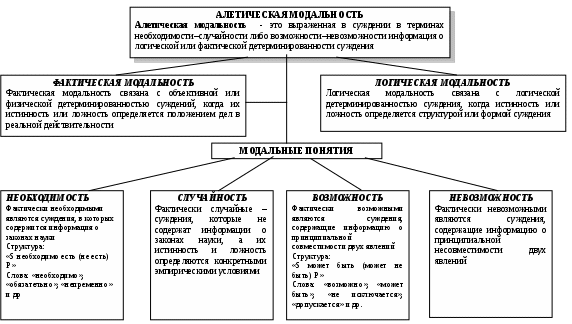 Схема 39. ВИДЫ МОДАЛЬНОСТЕЙ (эпистемическая модальность) 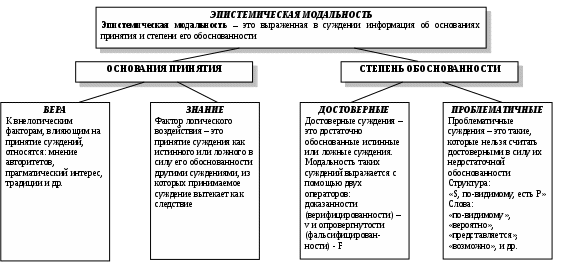 Схема 40. ВИДЫ МОДАЛЬНОСТЕЙ (деонтическая модальность) 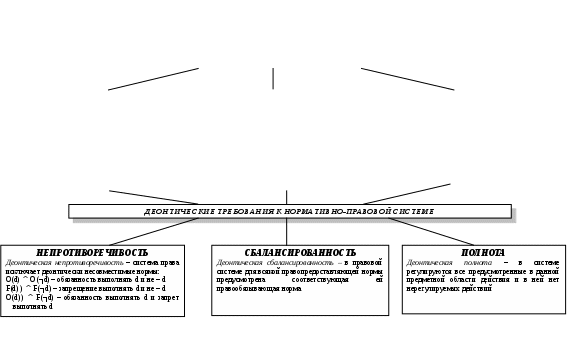 ДЕОНТИЧЕСКАЯ МОДАЛЬНОСТЬ Деонтическая модальность – это выраженное в суждении предписание в форме совета, пожелания, правила поведения или приказа, побуждающее человека к конкретным действиям К деонтическим относят и нормы права. В соответствии с деонтическими операторами (О – обязывание, F – запрещение, Р – разрешение) среди норм права различают: ПРАВООБЯЗЫВАЮЩИЕ Правообязывающие нормы формулируют с помощью слов: «обязан», «должен», «надлежит», «признается» и др. Символическая запись правообязывания: О(d), что означает «действие» d подлежит обязательному исполнению Пример: «Организация обязана возместить вред, причиненный по вине ее работников» ПРАВОЗАПРЕЩАЮЩИЕ Правозапрещающие нормы формулируют с помощью слов: «запрещается», «не вправе», «не может», «не допускается» и др. Символическая запись правозапрещения: F(d), что означает «действие d запрещается» Пример: «Запрещается домогаться показаний обвиняемого путем насилия, угроз и иных незаконных мер» ПРАВОПРЕДСТАВЛЯЮЩИЕ Правопредставляющие нормы формулируют с помощью слов: «имеет право», «может иметь», «может принять» и др. Символическая запись правопредставления: P(d), что означает «предоставляется право выполнить d» Пример: «Наниматель жилого помещения имеет право в любое время расторгнуть договор. Схема 41. СТРУКТУРА УМОЗАКЛЮЧЕНИЯ 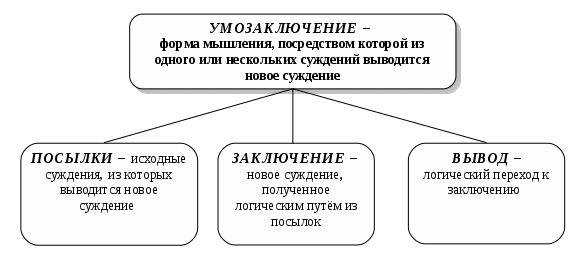 Схема 42. КЛАССИФИКАЦИЯ УМОЗАКЛЮЧЕНИЙ (по направленности логического следования)                Схема 43. ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ ОБРАЩЕНИЕ Категорический силлогизм с выделяющими суждениями Умозаключения логики суждений      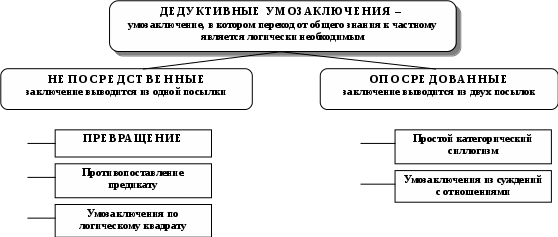 Схема 44. ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ (структура силлогизма)          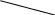 БОЛЬШИЙ ТЕРМИН (Р) – предикат заключения БОЛЬШАЯ ПОСЫЛКА – суждение, в которое входит больший термин СРЕДНИЙ ТЕРМИН (М) – встречается в посылках, но не встречается в заключении  МЕНЬШАЯ ПОСЫЛКА – суждение, в которое входит меньший термин  МЕНЬШИЙ ТЕРМИН (S) – субъект заключения Схема 45. ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ (структура силлогизма) 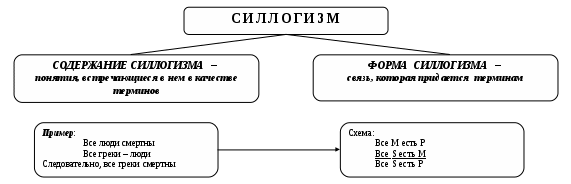 Правильность силлогизмане зависит от его содержания, а зависит только от его формы. Правомерность вывода, т.е. логического перехода от посылок к заключению, в категорическом силлогизме основывается на положении (аксиоме силлогизма): все, что утверждается или отрицается относительно всех предметов некоторого класса, утверждается или отрицается относительно каждого предмета и любой части предметов этого класса. Схема 46. ОБЩИЕ ПРАВИЛА КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА (правила терминов) 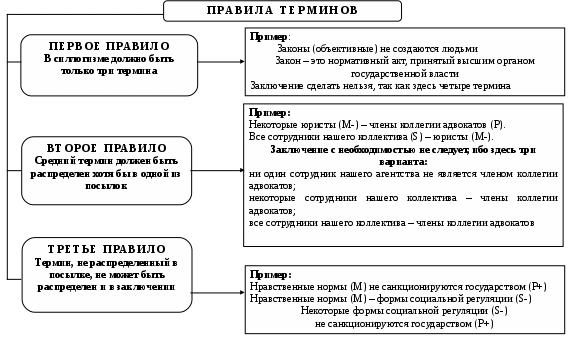 Схема 47. ОБЩИЕ ПРАВИЛА КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА (правила посылок) 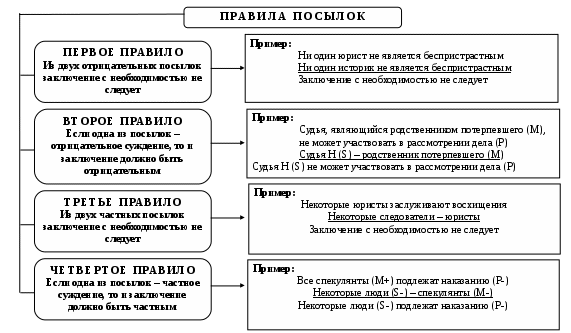 Схема 48. ФИГУРЫ И МОДУСЫ КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА ( I фигура)  Схема 49. ФИГУРЫ И МОДУСЫ КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА (II фигура)  Схема 50. ФИГУРЫ И МОДУСЫ КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА (III фигура)  Схема 51. ФИГУРЫ И МОДУСЫ КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА (IV фигура)  Схема 52. ЛОГИЧЕСКИЕ ОСНОВЫ АРГУМЕНТАЦИИ (аргументация) 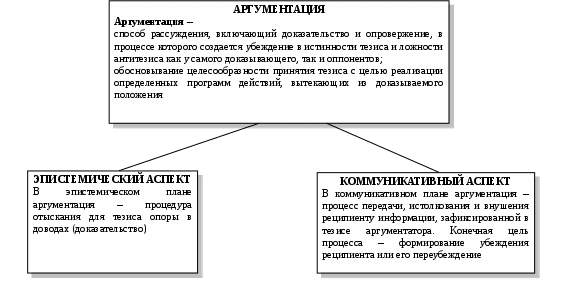 Схема 53. ЛОГИЧЕСКИЕ ОСНОВЫ АРГУМЕНТАЦИИ (виды аргументации) ОПРОВЕРЖЕНИЕ – полное обоснование ложности какого-либо высказывания Цель – категорическое отрицание тезиса ПОДТВЕРЖДЕНИЕ – частичное обоснование истинности Цель – усиление тезиса и повышение убедительности доказательства ВОЗРАЖЕНИЕ – частичное обоснование ложности некоторых высказываний (критика) Цель – ослабление тезиса и указание на его недоказан-ность. Подтверждение антитезиса ИНТЕРПРЕТАЦИЯ – приписывание некоторого содержательного смысла или значения символам и формам формальной системы. Цель – обоснование знания  ОПРАВДАНИЕ – подведение под некоторое умственное или практическое действие определенного ценностного соображения (довода) в процессе логического обоснования Цель – повышение убедительности доказательств        ДОКАЗАТЕЛЬСТВО – полное обоснование истинности какого-либо высказывания Цель – категорическое утверждение тезиса ОБЪЯСНЕНИЕ – выявление причины, следствием которой выступает явление, требующее логического обоснования Цель – повышение убедительности доказательств Схема 54. ЛОГИЧЕСКИЕ ОСНОВЫ АРГУМЕНТАЦИИ (структура доказательства) ДОКАЗАТЕЛЬСТВО – логическая процедура установления истинности какого-либо утверждения при помощи других утверждений, истинность которых уже установлена ФОРМА ДОКАЗАТЕЛЬСТВА (ДЕМОНСТРАЦИЯ) – логический способ обоснования тезиса при помощи аргументов (возможно, с использованием промежуточных допущений) ПРОМЕЖУТОЧНЫЕ ДОПУЩЕНИЯ – вспомогательные допущения, которые вводятся в процессе рассуждения (дедукции) и устраняются затем при переходе к окончательному результату рассуждения АРГУМЕНТЫ – высказывания, посредством которых осуществляется доказательство тезиса Виды аргументов              ТЕЗИС ДОКАЗАТЕЛЬСТВА – высказывание, истинность или ложность которого доказывается Схема 55. ЛОГИЧЕСКИЕ ОСНОВЫ АРГУМЕНТАЦИИ (виды доказательств, часть I) ДОКАЗАТЕЛЬСТВА | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

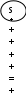
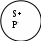

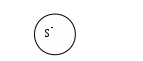
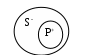 частновыделяющие
частновыделяющие