Расчетно-аналитическая работа. Государственное бюджетное образовательное учреждение высшего образования омский государственный аграрный университет им. П. А. Столыпина
 Скачать 67.5 Kb. Скачать 67.5 Kb.
|
Вариант 19 Задача Организация располагает пашней площадью 3300 га, на которой планируется разместить 6 культур: пшеницу, овес, ячмень, горох, рожь и кукурузу. Для возделывания указанных культур в наличии имеются следующие ресурсы: трудовые ресурсы- 90900чел.-час., материально-денежные - 2690000руб. и ресурс техники - 90400машино-часов. Дополнительное условие: площадь посева пшеницы должна превышать площадь посева всех остальных культур. Определить оптимальное соотношение площадей посевов указанных культур, при котором выручка от реализации продукции в хозяйстве будет максимальной. Таблица 1 – Исходные данные для решения задачи
Решение. Запишем математическую модель задачи: определить значения переменных: 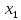 , , 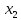 , , 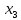 , , 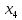 , , 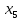 , , 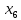 , удовлетворяющих следующей системе ограничений: , удовлетворяющих следующей системе ограничений: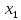 + +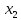 + +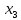 + +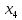 + +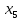 + +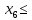 3300 – по площади пашни, га; 3300 – по площади пашни, га;32 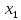 + +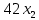 + +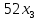 + +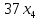 + +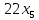 + +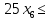 90900 – по трудовым ресурсам, чел.-час.; 90900 – по трудовым ресурсам, чел.-час.;320 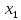 + +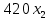 + +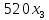 +370 +370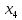 + +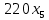 + +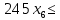 2690000 – по материально-денежным ресурсам, руб.; 2690000 – по материально-денежным ресурсам, руб.;38 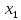 + +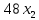 + +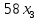 + +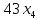 + +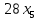 + +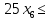 90400 – ресурсу техники, машино-час.; 90400 – ресурсу техники, машино-час.;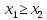 + +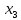 + +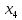 + +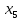 + +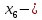 по дополнительному условию: площадь посева пшеницы должна превышать площадь посева всех остальных культур, это условие перепишем в виде: по дополнительному условию: площадь посева пшеницы должна превышать площадь посева всех остальных культур, это условие перепишем в виде: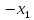 + +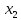 + +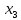 + +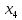 + +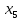 + +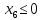 ; ;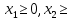 0, 0,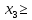 0 0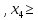 0, 0,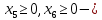 условие неотрицательности переменных и обеспечивающих максимальное значение целевой функции: условие неотрицательности переменных и обеспечивающих максимальное значение целевой функции: Z = 336 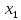 + +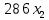 + +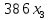 + +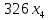 + +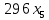 + +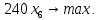 Чтобы решить данную задачу линейного программирования симплексным методом, она должна быть представлена в канонической форме, система ограничений приведена к единичному базису, свободные члены уравнений должны быть неотрицательны. Для построения первого опорного плана систему неравенств приведем канонической форме путем введения дополнительных (базисных) переменных 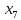 , , 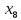 , , 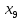 , , 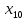 , , 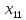 . В том случае, если неравенство имеет знак . В том случае, если неравенство имеет знак 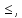 базисная переменная добавляется в неравенство со знаком «+», если знак неравенства базисная переменная добавляется в неравенство со знаком «+», если знак неравенства 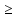 , базисная переменная добавляется со знаком « , базисная переменная добавляется со знаком «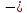 ». В нашем примере все неравенства со знаком ». В нашем примере все неравенства со знаком 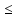 , следовательно, базисные переменные , следовательно, базисные переменные 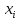 i=7,…,11, добавляются со знаком «+»: i=7,…,11, добавляются со знаком «+»: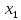 + +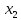 + +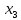 + +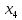 + +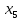 + +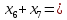 3300 330032 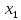 + +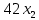 + +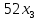 + +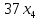 + +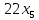 + +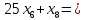 90900 90900320 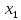 + +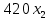 + +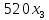 +370 +370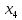 + +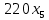 + +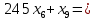 2690000 269000038 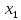 + +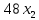 + +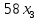 + +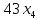 + +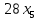 + +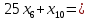 90400 90400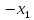 + +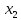 + +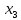 + +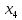 + +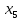 + +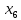 + +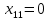 ; ;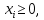 i=1, 2, 3, …, 11 i=1, 2, 3, …, 11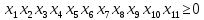 ; ;Z=336 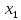 + +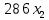 + +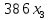 + +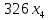 + +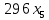 + +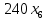 + +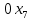 + +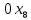 + +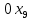 + +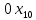 + +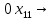 max maxCоставим первую симплексную таблицу. Она представляет собой форму выражения первого опорного плана. Коэффициенты, стоящие в Z- строке, показывают, как изменяется значение целевой функции при единичном изменении соответствующей свободной переменной. И называются эти коэффициенты оценкой или индексом этой свободной переменной. А сама строка Z называется индексной или оценочной. В первом столбце перечисляют базисные переменные. Во второй столбец записывают оценки базисных переменных, указанные в целевой функции. В третьем столбце указывают свободные члены. В остальных столбцах таблицы записывают коэффициенты при свободных переменных по соответствующим уравнениям. Над рабочей частью таблицы перечисляют свободные переменные. Сверху над свободными переменными помещают оценки свободных переменных, указанные в целевой функции. Над столбцом свободных членов записывают свободный член целевой функции (если таковой имеется) с противоположным знаком. Оценки Z – строки рассчитывают по форме: 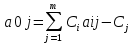 где j =1, 2,…,n 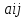 – коэффициенты j – ого столбца, – коэффициенты j – ого столбца,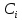 – коэффициенты при базисных переменных в уравнении Z, – коэффициенты при базисных переменных в уравнении Z,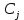 – коэффициенты при свободных переменных в уравнении Z. – коэффициенты при свободных переменных в уравнении Z.Таблица 2 – Заполнение первой симплексной таблицы (опорного плана)
В симплексных таблицах формальным признаком оптимальности является содержание оценочной строки (Z-строки). Исходное опорное решение записывается по столбцу свободных членов. Так как свободным переменным в указанном столбце не соответствуют свободные члены, то 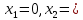 0, 0,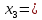 0 0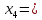 0, 0,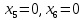 . Базисным переменным соответствуют определенные свободные члены . Базисным переменным соответствуют определенные свободные члены 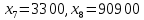 , , 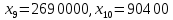 , ,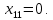 Следовательно, опорное решение записывается так: Xоп.(0, 0, 0, 0, 0, 0, 3300, 90900, 2690000, 90400, 0), Zmax=0. Переходим к основному алгоритму симплекс-метода. Таблица 3 – Симплексная таблица (исходное опорное решение)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

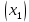
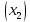
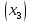
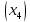
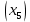
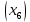
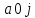
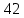
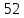
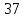
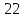
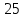
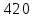
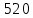
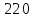
 /
/