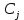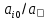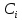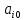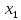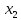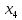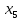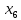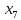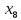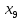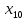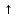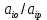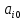Расчетно-аналитическая работа. Государственное бюджетное образовательное учреждение высшего образования омский государственный аграрный университет им. П. А. Столыпина
 Скачать 67.5 Kb. Скачать 67.5 Kb.
|
|
Так как мы решаем задачу на максимум, для достижения оптимального решения все числа в Z-строке должны быть отрицательными. Поэтому опорный план не является оптимальным. Для перехода к следующей таблице выбираем разрешающий столбец (при решении на максимум по наибольшей по модулю отрицательной оценке (-386)). Далее считаем симплексные отношения (последний столбец): 3300/1=3300, 90900/52=1748,07, 2690000/520=5173,07, 90400/58=1558,62, 0/1=0. В первой симплексной таблице нашего примера все коэффициенты оценочной строки отрицательны. Следовательно, согласно теореме, план (на максимум целевой функции) не является оптимальным и требует улучшения. По наименьшему симплексному отношению выбираем разрешающую строку и переходим ко второй симплексной таблице (таблица 4). Таблица 4 – Вторая симплексная таблица
Во второй симплексной таблице свободная переменная разрешающего столбца ( 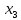 ) переходит на место базисной переменной разрешающей строки ( ) переходит на место базисной переменной разрешающей строки (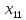 ), а ), а 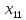 – на место – на место 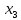 . . Далее в разрешающем столбце на месте бывшего разрешающего элемента записываем обратную величину: 1/(1)= 1*. Все остальные элементы бывшего разрешающего столбца делим на разрешающий элемент и записываем с противоположным знаком: 1/(1)*(–1) = –1*, 52/(1) * (–1) = –52*, 520/(1)*(–1) = –520* и тд. Для нахождения остальных элементов разрешающей строки необходимо коэффициенты бывшей разрешающей строки разделить на разрешающий элемент: 0*=0/(1), –1*= –1/(1) и т.д. Все остальные элементы таблицы находятся по правилу прямоугольника по следующей схеме: бывший коэффициент – (коэффициент разрешающей строки * коэффициент разрешающего столбца)/разрешающий элемент. Например: 2* = 1 – (–1*1)/(1), 84* = 32 – (–1*52)/(1) и т.д. Оценки Z-строки в таблице 4 указывают на неоптимальность плана, так как имеются отрицательные элементы. Он единственный, поэтому в качестве разрешающего столбца выбирается столбец с отрицательным элементом. Далее весь алгоритм повторяется снова. В результате получаем следующую симплексную таблицу (таблица 5). Считаем симплексные отношения (последний столбец), и выбираем из них наименьшее. Таблица 5 – Третья симплексная таблица
|