Градиентный спуск

• Название: Градиентный спуск
• Дата: 23.12.2021
• Размер: 1.14 Mb.
• Имя файла: 27lek.docx
• Тип: Документы; #314868

Градиентный спуск

https://craftappmobile.com/gradient-descent-and-theano-library/

https://smartiqa.ru/blog/neural-network-gradient-descent

Введение в градиентный спуск

Подробнее рассмотрим градиентный спуск, так как он широко используется в машинном обучении и является настолько общим методом, что может быть полезен в разнообразнейших ситуациях.

Суть в следующем. Пусть у вас есть функция, минимум которой вы хотите найти, и пусть вам нужно найти такие входные данные, при которых функция была бы в минимуме. Как правило, мы хотим минимизировать функцию затрат или ошибок. Может потребоваться также и найти максимумы – например, когда мы ищем максимум для функции правдоподобности некоторого распределения вероятностей. Всё, что нужно сделать – это просто поменять местами стороны. Чтобы объяснить это, рассмотрим очень простой одномерный пример. Как правило, в машинном обучении мы используем размерности, гораздо большие единицы, но этот пример позволит наглядно увидеть суть.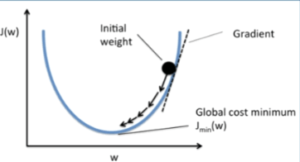



Итак, пусть у нас есть простая функция J=w². Мы знаем, что минимум функции при w=0, но, предположим, мы этого не знаем. Наш весовой коэффициент установим случайным образом. Предположим, w=20. Мы знаем, что производная dJ/dw равна 2w. Установим коэффициент обучения равным 0,1. В первом приближении мы имеем:

w – 0,1*2w = 20 – 0,1*40 = 16.

Поэтому установим w=16. Во втором приближении

w – 0,1*2w = 16 – 0,1*2*16 = 12,8.

Это даёт нам новое значение w=12,8. В третьм приближении

w – 0,1*2w = 12,8 – 0,1*2*12,8 = 10,24.

Как вы можете видеть, на каждом шаге мы всё ближе и ближе к нулю, зато каждый шаг становится меньшим, так как при приближении к нулю наклон становится меньше.

Теперь давайте попробуем реализовать это в коде и посмотрим, сможем ли мы полностью дойти до нуля. Импортируем библиотеку NumPy, установим значение w=20 и будем печатать результат на каждом шаге итераций. Количество приближений установим равным 30.

import numpy as np

w = 20

for i in x range(30):

w = w – 0.1*2*w

print w

Как видим, w достигает значения 0,02, так что, похоже, 30 приближений недостаточно. Попробуем 100 приближений.

w = 20

for i in x range(100):

w = w – 0.1*2*w

print w

Теперь результат равен 4,07*10^-9 – это очень близко к нулю.

Медленно продвигаясь в направлении градиента функции, мы всё ближе и ближе подходим к минимум этой функции.

Почему этот метод так важен? По мере продвижения далее в глубокое обучение и машинное обучение функции будут становиться всё более сложными. Для нейронных сетей с softmax нахождение производной может занять у вас несколько часов или даже дней. При переходе к свёрточным и рекуррентным нейронным сетям градиенты, конечно, можно найти на бумаге, но нет никакого желания тратить на это время. Куда лучше потратить время на проверку различных архитектур и параметров, не заботясь о градиентах. Тем более, что для вычисления градиентов можно использовать специальные библиотеки, такие как Theano и TensorFlow.

Впрочем, весьма желательно понимать, что происходит, потому что тогда вычисление градиентов становится ещё одним инструментом в нашем инструментарии по машинному обучению, и мы можем применять его где угодно, даже в таких вещах, как скрытые марковские модели.

В качестве упражнения попытайтесь найти градиент и решение для следующей функции затрат, используя градиентный спуск.

J(w₁, w₂) = w₁² + w₂⁴.

Градиент

Чтобы понять, откуда нейронная сеть узнает, как ей поменять свои параметры (параметрами будем называть веса связей) для уменьшения ошибки, нужно разобраться в том, что такое градиент. На самом деле, градиент (в математике) ‒ это просто стрелочка, которая указывает, в каком направлении функция растет быстрее всего. Звучит, наверное, сложно, но суть очень простая. Давайте посмотрим на график параболы y=x².



График параболы с отмеченной точкой А и градиентом в ней

На рисунке мы отметили точку А с координатами (2, 4) и визуализировали градиент в ней. Видно, что получилась голубая стрелочка указывающая в направлении роста. Возможно у читателя возникнет вопрос, почему стрелка направлена именно так. Ответ кроется в глубинах математики, но если коротко, то это связано со скоростью роста функции в этой точке (с ее производной). Странный значок перед y называется набла, это общепринятое обозначение градиента. Такая запись говорит: вот здесь начерчен градиент функции y(x).

Суть градиента действительно проста, и я уверен, что читатель уже уловил ее, но все же приведу здесь еще один рисунок. На нем изображена уже более сложная функция, зависящая не от одной, а от двух переменных.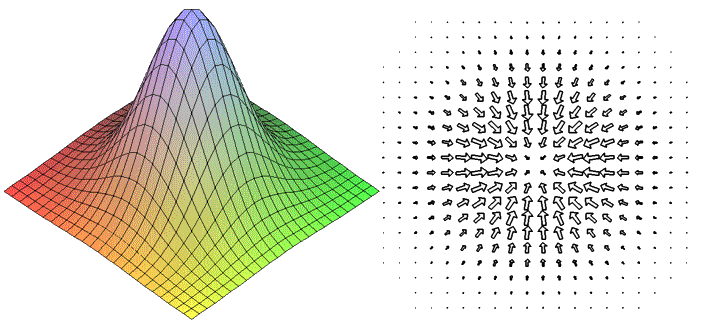



График многомерной функции и изображение ее градиента

Слева на рисунке изображен график какой-то сложной функции, для наглядности он окрашен в разные цвета. Справа ‒ градиент этой функции. Как можно видеть, стрелки указывают в направлении наискорейшего роста, причем чем "круче" "холмик", тем длиннее стрелка для этого участка. Таким образом градиент показывает, в каком направлении функция растет скорее всего.

А причем тут нейросети?

Разобравшись в том, что же такое градиент, читатель задастся вопросом: причем тут нейросети? Ответ очевиден. Помните, нейросеть должна каждый раз находить ошибку между результатом своей работы и верным ответом, а затем определять, как менять веса для уменьшения ошибки. Оказывается, существует очень-очень сложная зависимость ошибки от всех параметров нейросети. То есть

L = f(w1, w2, w3, …, wn),

где L – это ошибка, а f(w1, w2, w3, …, wn) – функция от весов связей в нейронной сети. Думаю, тут стоит прояснить, почему ошибка зависит от параметров модели (так мы иногда будем называть нейросети): нейронная сеть не может повлиять на ответ, подготовленный человеком, но она может изменить свой ответ (который как раз и зависит от всех параметров модели) так, чтобы ошибка стала меньше.

То есть главная задача нейросети во время обучения ‒ найти минимум функции ошибки ‒ то есть вычислить такие значения весов связей, что при них ошибка будет минимальной (то есть ответ нейросети будет максимально приближен к ответу, подготовленному человеком).

И тут перед нами открываются чудеса математики, а именно ‒ антиградиент. Оказывается, если градиент, указывающий в направлении наискорейшего роста функции, просто развернуть на 180 градусов, то он будет указывать в противоположном направлении: направлении наискорейшего убывания функции. Это замечательное свойство поможет нам постепенно "спуститься" к минимуму функции ошибки.

Читайте также

[ Нейросети Часть 3 ] Откуда нейросеть знает, что на картинке котик? Все, что вы хотели знать о сверточных нейросетях

В статье рассказывается о принципе работы сверточных нейронных сетей

Градиентный спуск

Наконец, мы дошли до самого метода градиентного спуска. Становится понятно: "спуск" ‒ потому что мы спускаемся к минимуму функции ошибки, а "градиентный" ‒ потому что мы используем градиент, чтобы понять, как изменять веса связей, в каком направлении нам спускаться, чтобы быстрее всего прийти к минимуму.

Вычисление градиента для сложных функций (таких, как, например, зависимость ошибки от параметров модели) ‒ очень математически сложный процесс. В нейронных сетях это делается постепенно с последнего слоя до первого (на то есть математические причины). Когда градиент вычислен, мы делаем один шаг спуска в направлении, противоположном направлению градиента (напомню: градиент показывает, куда растет функция, а мы хотим пойти туда, где функция убывает).

Тут есть множество тонкостей, например, на каждом шаге спуска мы умножаем значение градиента на постоянную величину от 0 до 1 (эта величина подбирается человеком), чтобы не шагнуть слишком далеко. Может возникнуть такая ситуация, что минимум находится слева от нас, мы шагаем чересчур далеко, и вот минимум уже справа от нас, шагаем еще раз ‒ минимум опять слева, и так до бесконечности. Такой случай со знакомой нам параболой приведен в анимации ниже.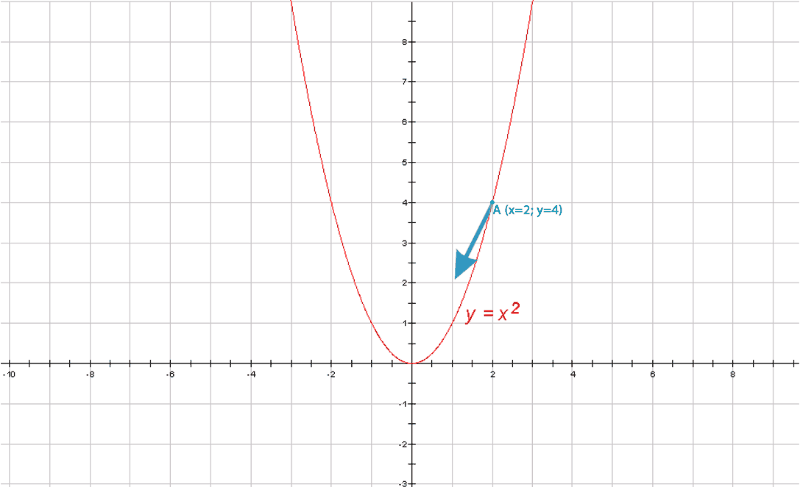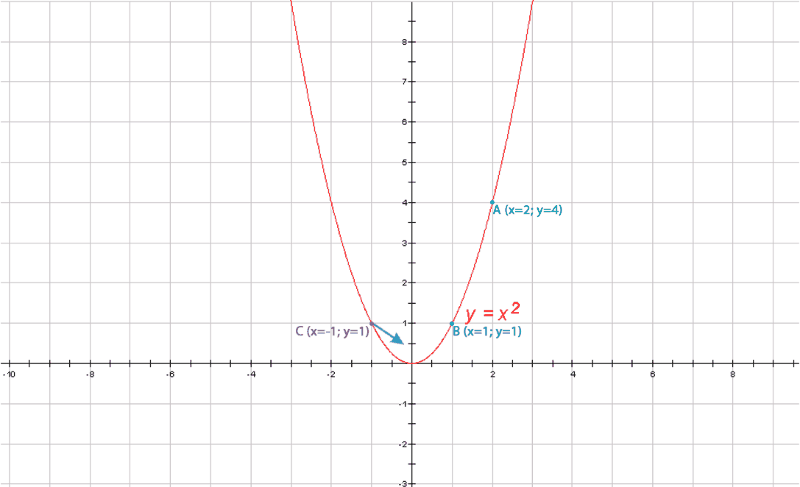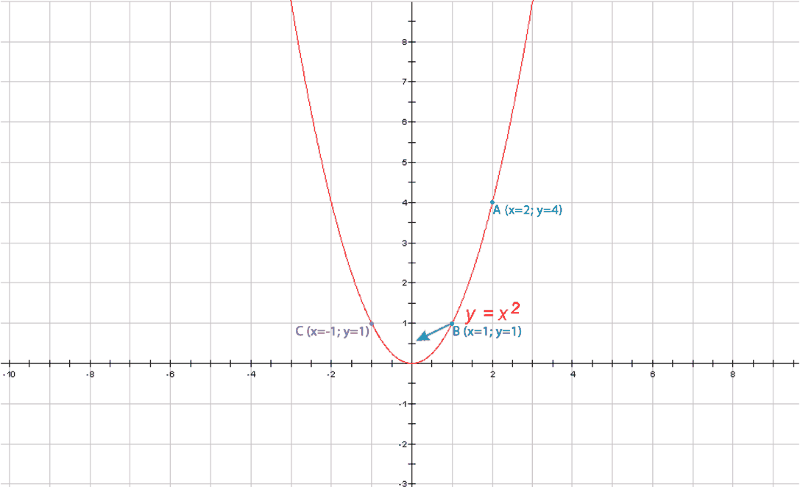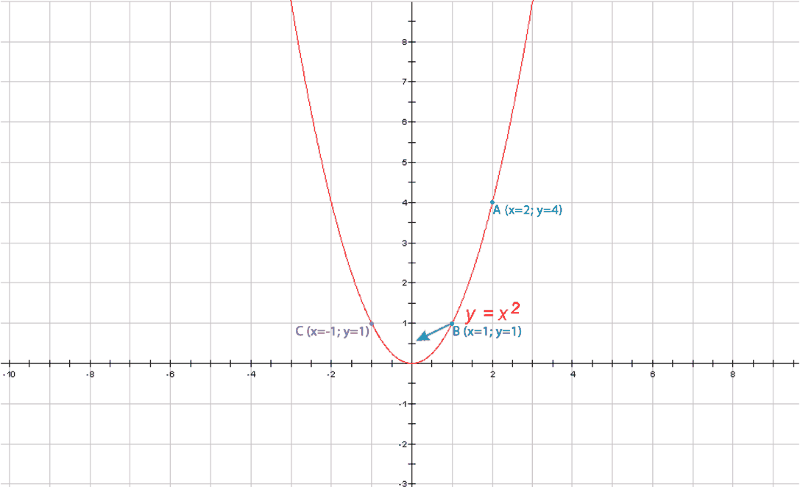



Пример неудачного градиентного спуска

Как видно из анимации, из-за слишком большого значения градиента вблизи точки (0, 0), мы постоянно "перескакиваем" минимум, поэтому и нужно умножать градиент на число от 0 до 1, а спуск к минимуму делать плавным.

Напоследок

Сегодня мы узнали, что такое градиентный спуск, и какое он имеет отношение к обучению нейронных сетей. Хотелось бы отметить, что это только вершина айсберга, под которой находится дифференциальное, матричное и векторное исчисления и линейная алгебра. Довольно грубо называть градиент "стрелкой", тем не менее, такое обозначение отлично объясняет его суть.

Стоит также отметить, что функции ошибки в нейронных сетях обычно многотысячемерные (это значит, что функция зависит не от одного, не от двух, а от тысяч разных переменных), и именно из-за многократного вычисления градиента (его нужно вычислять после каждого цикла обучения) обучение больших нейронных сетей занимает от нескольких часов до дней и недель.

Ну, и в самом конце, приведу красивую анимацию градиентного спуска для одной из функций, чтобы вы поняли, что математика бывает очень красивой наукой.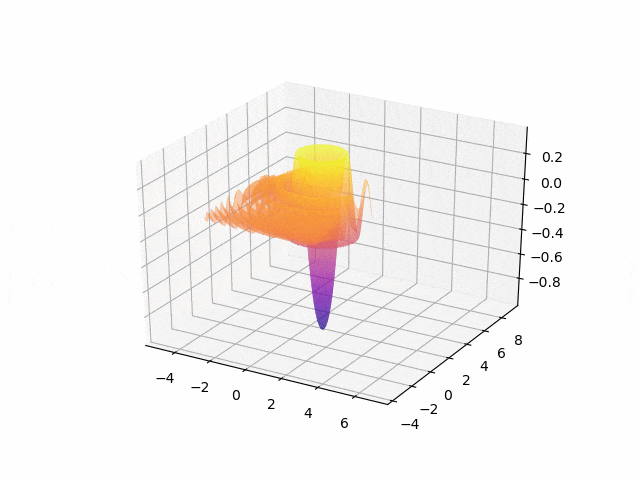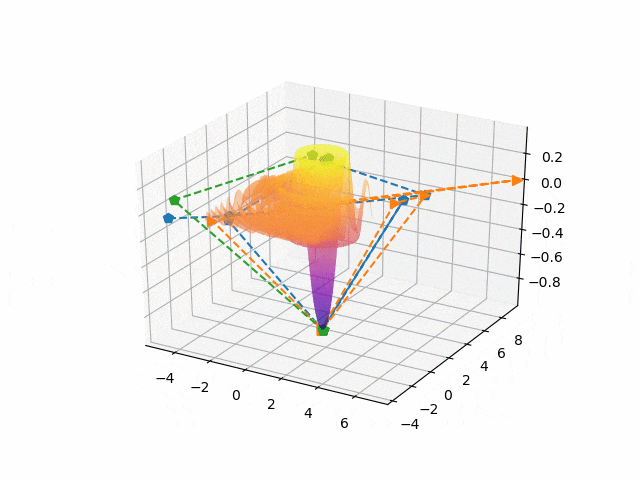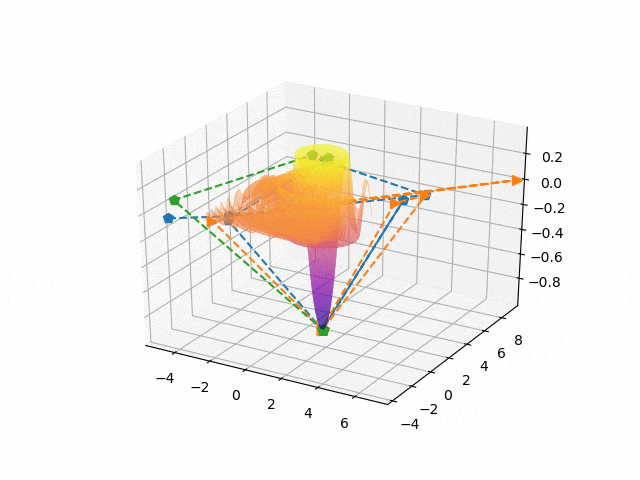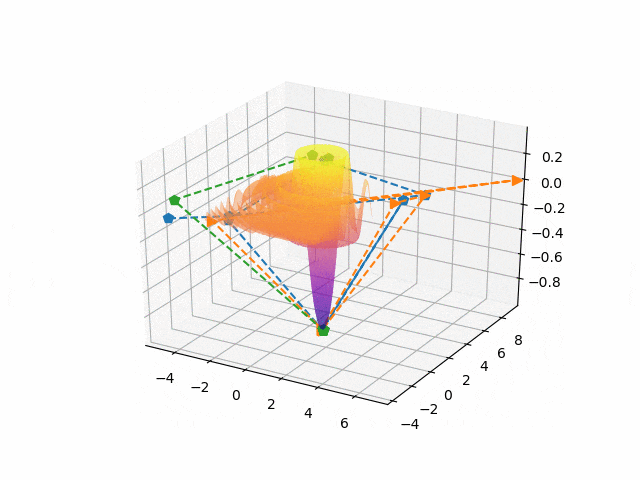



Пример градиентного спуска