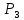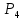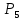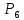Решение военно-прикладных задач численными методами линейного программирования. Решение_военно-прикладных_задач_численными_методами_линейного_пр. Графоаналитический метод. Задача 1
 Скачать 47.98 Kb. Скачать 47.98 Kb.
|
|
Ввод. Современное общество развивается с огромной скоростью. Появляются различные задачи, направленные на необходимость оптимизации решения, с точки зрения поставленной цели. Известно, что наиболее разработанными и хорошо распространёнными являются математические модели, которые реализуются, с помощью методов линейного программирования. В настоящее время новейшие достижения математики и современной вычислительной техники находят все более широкое применение в экономических, военных, инженерных и других исследованиях и планировании. Этому способствует развитие определённых разделов математики, таких как математическое программирование, теория игр, теория массового обслуживания, а также бурное развитие быстродействующей техники. Уже накоплен достаточный опыт постановки и решения экономических задач с помощью математических методов. Особенно успешно развиваются методы оптимального планирования, которые и составляют сущность математического программирования. Линейное программирование – это наука о методах исследования и отыскания наибольших и наименьших значений линейной функции, на неизвестные которой наложены линейные ограничения. Таким образом, задачи линейного программирования относятся к задачам на условный экстремум функции. Графоаналитический метод. Задача №1. На изготовление двух видов продукции 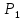 и и 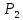 требуется три вида сырья требуется три вида сырья 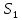 , , 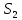 и и 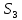 . Запасы каждого вида сырья ограничены и составляют соответственно . Запасы каждого вида сырья ограничены и составляют соответственно 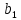 , , 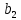 и и 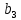 . При заданной технологии количество сырья, необходимое для изготовления единицы каждого из видов продукции известно и задано таблицей 1. . При заданной технологии количество сырья, необходимое для изготовления единицы каждого из видов продукции известно и задано таблицей 1.
Таблица 1 Необходимо: составить такой план выпуска продукции видов 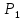 и и 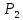 , при котором прибыль от реализации всей продукции была бы максимальной. , при котором прибыль от реализации всей продукции была бы максимальной.Замечание. Число 0 означает, что на производство продукции вида 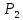 сырья вида сырья вида 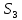 не требуется. не требуется.Решение. Обозначим через 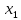 и и 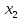 количество единиц продукции видов количество единиц продукции видов 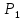 и и 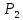 , планируемое к выпуску. Составим математическую модель задачи: , планируемое к выпуску. Составим математическую модель задачи: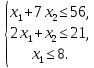 - система ограничений - система ограничений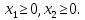 Любое решение 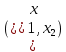 системы ограничений называется планом выпуска продукции или планом задачи. системы ограничений называется планом выпуска продукции или планом задачи.Суммарная прибыль предприятия от реализации продукции видов 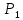 и и 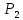 , выпущенной согласно плану , выпущенной согласно плану 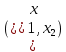 , равна , равна 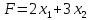 условных денежных единиц. По условию задачи требуется найти такой план условных денежных единиц. По условию задачи требуется найти такой план 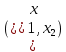 , при котором прибыль была бы максимальной, что принято обозначать так: , при котором прибыль была бы максимальной, что принято обозначать так: 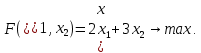 Линейная функция двух переменных 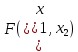 называется целевой функцией задачи. называется целевой функцией задачи.Таким образом, получили задачу линейного программирования: 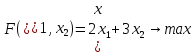 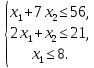 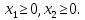 Построим область допустимых решений системы ограничений, которая представляет собой выпуклый многоугольник. Для этого запишем уравнения граничных прямых и построим их графики: 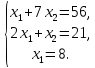  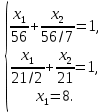 Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника ABCDE решений. Построим градиент функции цели 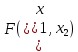 . .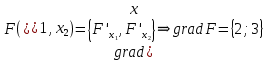 Построим линию нулевого уровня l, перпендикулярную grad F. Будем перемещать прямую lв направлении градиента до пересечения с последней вершиной многоугольника. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией. Прямая F = const пересекает область в точке С. Так как точка С получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых: 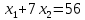 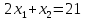 Решив систему уравнений, получим: 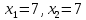 . Откуда найдем максимальное значение целевой функции: . Откуда найдем максимальное значение целевой функции: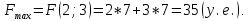 Ответ: для обеспечения максимальной прибыли от реализации готовой продукции предприятию необходимо выпускать 7 единиц продукции 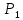 и 7 единиц продукции вида и 7 единиц продукции вида 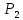 , при таком плане прибыль от реализации составит 35 условных денежных единиц. , при таком плане прибыль от реализации составит 35 условных денежных единиц.Симплекс-Метод. Задача №2. Для изготовления различных видов изделий A, B и С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице 2.
Таблица 2 Необходимо: составить план производство изделий, при котором общая стоимость всей производственной продукции является максимальной. Решение. Составим математическую модель задачи. Искомый выпуск изделий А обозначим через 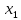 , изделий В – через , изделий В – через 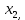 изделий С – через изделий С – через 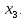 Так как каждый вид сырья имеет ограничения, переменные 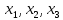 должны удовлетворять вот такой системе неравенств: должны удовлетворять вот такой системе неравенств: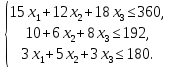 Общая стоимость произведенной продукции при условии выпуска 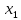 изделий А, изделий А, 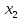 изделий В и изделий В и 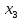 изделий С составляет: изделий С составляет: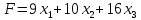 Переменные 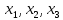 по своему экономическому содержанию могут принимать только неотрицательные значения: по своему экономическому содержанию могут принимать только неотрицательные значения: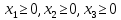 Таким образом мы пришли к следующей задаче: Среди всех неотрицательных решений системы неравенств требуется найти такое, при котором функция принимает максимальное значение. Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Для этого введем три дополнительных переменных, в результате его получим следующую систему: 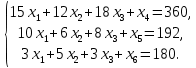 Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, 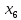 – это неиспользуемое количество сырья – это неиспользуемое количество сырья 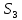 . .Для решения задачи составим симплекс-таблицу 2.1.
Таблица 2.1 При этом заполнение таблицы осуществляется следующим образом: В столбец Б таблицы записываются векторы базиса. В столбец 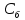 таблицы записываются коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса. таблицы записываются коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.В столбце 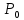 записываются положительные компоненты исходного опорного плана, в нем же в результате вычислений получаются положительные компоненты оптимального плана. записываются положительные компоненты исходного опорного плана, в нем же в результате вычислений получаются положительные компоненты оптимального плана.Столбцы вектора 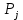 представляют собой коэффициенты разложения этих векторов по векторам данного базиса. представляют собой коэффициенты разложения этих векторов по векторам данного базиса.В таблице 2.1. первые mстрок (в данном случае три строки) определяются исходными данными задачи, а показатель (m+1) –й строки (в данном случае четвертой строки) вычисляются. В этой строке таблицы в столбце вектора 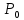 записывают значения целевой функции записывают значения целевой функции 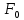 , которые она принимает при данном опорном плане? а в столбцах вектора , которые она принимает при данном опорном плане? а в столбцах вектора 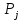 – значение – значение 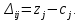 Значение 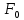 равно скалярному произведению вектора равно скалярному произведению вектора 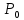 на вектор на вектор 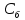 : :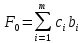 Значение 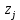 находят как скалярное произведение вектора находят как скалярное произведение вектора 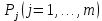 на вектор на вектор 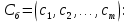 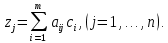 После заполнения таблицы исходный опорный план проверяется на оптимальность. Для этого просматриваются элементы (m+1) –й строки таблицы. В результате может иметь место один из следующих трех случаев: 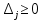 для j = m+1, m+1, …, n (при j = 1, …, m; для j = m+1, m+1, …, n (при j = 1, …, m; 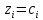 . Поэтому в данном случае числа . Поэтому в данном случае числа 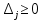 для всех jот 1 до n. В этом случае на основании признака оптимальности исходный опорный план является оптимальным. для всех jот 1 до n. В этом случае на основании признака оптимальности исходный опорный план является оптимальным.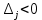 для некоторого j, и все соответствующие этому индексу величины для некоторого j, и все соответствующие этому индексу величины 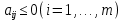 . В этом случае целевая функция не ограничена сверху на множестве планов. . В этом случае целевая функция не ограничена сверху на множестве планов.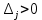 для некоторых индексов j, и для каждого такого j по крайней мере одно из этих чисел для некоторых индексов j, и для каждого такого j по крайней мере одно из этих чисел 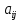 положительно. В этом случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится. положительно. В этом случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится.В качестве вектора, вводимого в базис, можно взять любой из векторов 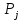 , имеющий индекс j, для которого , имеющий индекс j, для которого 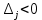 . Пусть, например, . Пусть, например, 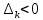 и решено ввести в базис вектор и решено ввести в базис вектор 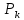 . .Для определения вектора, подлежащего исключению из базиса, находят 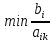 для всех для всех 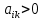 . Пусть этот минимум достигается при i = r. Тогда из базиса исключается вектор . Пусть этот минимум достигается при i = r. Тогда из базиса исключается вектор 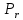 , а число , а число 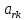 называют разрешающим элементом.Столбец и строка, на пересечении которых стоит разрешающий элемент, называют направляющими.После выделения направляющей строки и столбца находят новый опорный план и коэффициенты разложения векторов называют разрешающим элементом.Столбец и строка, на пересечении которых стоит разрешающий элемент, называют направляющими.После выделения направляющей строки и столбца находят новый опорный план и коэффициенты разложения векторов 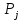 через векторы нового базиса соответствующего новому опорному плану. через векторы нового базиса соответствующего новому опорному плану.Переход от одного опорного плана к другому сводится к переходу от одной симплекс-таблицы к другой, правила заполнения которых состоят в следующем: В столбцах векторов, входящих в базис, на пересечении строк и столбцов одноименных векторов проставляются единицы, а все остальные элементы данных столбцов полагают равными нулю. Элементы векторов 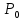 и и 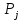 в строке новой симплекс - таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы делением их на величину разрешающего элемента. В столбце в строке новой симплекс - таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы делением их на величину разрешающего элемента. В столбце 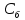 в строке вводимого вектора проставляют величину в строке вводимого вектора проставляют величину 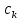 , где k – индекс вводимого вектора. , где k – индекс вводимого вектора.Остальные элементы столбцов вектора 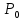 и и 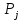 новой симплекс - таблицы вычисляют по правилу треугольника. Для вычисления какого-нибудь из этих элементов находят три числа: новой симплекс - таблицы вычисляют по правилу треугольника. Для вычисления какого-нибудь из этих элементов находят три числа:Число, стоящее в исходной симплекс – таблице на месте искомого элемента новой симплекс – таблицы; Число, стоящее в исходной симплекс – таблице на пересечении строки, в которой находится искомый элемент новой симплекс – таблицы, и столбца, соответствующего вектору, вводимому в базис; Число, стоящее в новой симплекс – таблице на пересечении столбца, в котором стоит искомый элемент, и строки вновь вводимого в базис вектора (как отмечено выше, эта строка получается из строки исходной симплекс – таблицы делением ее элементов на разрешающий элемент). Эти три числа образуют своеобразный треугольник, две вершины которого соответствуют числам, находящимся в исходной симплекс – таблице, а третья – числу, находящемуся в новой симплекс – таблице. Для определения искомого элемента новой симплекс – таблицы из первого числа вычитают произведение второго и третьего. После заполнения новой симплекс – таблицы просматриваются элементы (m+1) –й строки. Если все 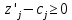 , то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то, используя описанную выше последовательность действий, находят опорный план. Этот процесс продолжается до тех пор, пока либо не получают оптимальный план задачи, либо не устанавливают ее неразрешимость. , то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то, используя описанную выше последовательность действий, находят опорный план. Этот процесс продолжается до тех пор, пока либо не получают оптимальный план задачи, либо не устанавливают ее неразрешимость.Замечание. При переходе от одного плана к другому значение функции может оставаться прежним. Более того, возможен случай, когда функция сохраняет свое значение в течение нескольких итераций, а также возможен возврат к первоначальному базису. В последнем случае обычно говорят, что произошло зацикливание. В индексной строке нет отрицательных элементов, значит, получен оптимальный план, при этом 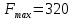 . Следовательно, план выпуска продукции, включающий 20 изделий С, является оптимальным. . Следовательно, план выпуска продукции, включающий 20 изделий С, является оптимальным.Ответ: при данном плане выпуска изделий полностью используется сырье 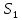 , а остается не использованным 32 кг сырья , а остается не использованным 32 кг сырья 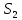 и 120 кг сырья и 120 кг сырья 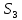 ; стоимость производимой продукции равна 320 руб. ; стоимость производимой продукции равна 320 руб. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||