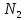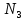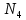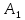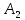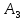Решение военно-прикладных задач численными методами линейного программирования. Решение_военно-прикладных_задач_численными_методами_линейного_пр. Графоаналитический метод. Задача 1

• Название: Графоаналитический метод. Задача 1
• Анкор: Решение военно-прикладных задач численными методами линейного программирования
• Дата: 24.12.2021
• Размер: 47.98 Kb.
• Имя файла: Решение_военно-прикладных_задач_численными_методами_линейного_пр.docx
• Тип: Документы; #316879
• страница: 2 из 3

Решение транспортной задачи. Задача №3.

На складах вооружения 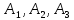имеются запасы комплектов количестве 30, 60 и 10 у.е. соответственно.

Найти такой вариант прикрепления воинских частей к складам вооружения, при котором сумма затрат на перевозку была бы минимальной.

Склады вооружения	Потребители				Запасы
	8	7	12	11	30
	10	4	3	5	60
	9	6	1	2	10
Потребности	40	20	10	30	100

Таблица 3

Решение. А) Проверим необходимое и достаточное условие разрешимости задачи.

∑а (Запасы) = 30 + 60 + 10 = 100

∑b (Потребности) = 40 + 20 + 10 + 30 = 100

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, данная модель транспортной задачи является закрытой. Первый опорный план находим методом наименьшей стоимости.

1. 
   Выбираем в таблице 3 клетку с наименьшим тарифом перевозок – это клетка - (3,3).
   

Потребности – 10 ед.

Запасы – 10 ед.

Min (10, 10) = 10 ставим в клетку (3, 3), при этом исключаем третью строку из рассмотрения, а запасы третьего столбца уменьшаем на 10 ед. и переходим к новой таблице 3.1

Склады вооружения	Потребители				Запасы
	8	7	12	11	30
	10	4	3	5	60
Потребности	40	20	0	30	90

Таблица 3.1

2. 
   Наименьшая стоимость – 4,
   

Клетка – (2,2).

Потребности – 20 ед.

Запасы – 60 ед.

Min (30, 60) = 20 ставим в клетку (2, 2), при этом второй столбец исключаем из рассмотрения, а запасы второй строки уменьшаем на 20 и переходим к новой таблице 3.2:

Склады вооружения	Потребители				Запасы
	8		12	11	30
	10		3	5	40
Потребности	40		0	30	70

Таблица 3.2

3. 
   Наименьшая стоимость – 5,
   

Клетка – (2, 4).

Потребности – 30 ед.

Запасы – 40 ед.

Min (40, 30) = 30 ставим в клетку (2, 4), при этом последний столбец исключаем из рассмотрения, а запасы второй строки уменьшаем на 30 и переходим к новой таблице 3.3:

Склады вооружения	Потребители				Запасы
	8		12		30
	10		3		10
Потребности	40		0		40

Таблица 3.3

4. 
   Наименьшая стоимость – 8,
   

Клетка – (1,1).

Потребности – 40 ед.

Запасы – 30 ед.

Min (40, 30) = 30 ставим в клетку (1, 1), при этом исключаем первую строку из рассмотрения, а запасы первого столбца уменьшаем на 30 и переходим к новой таблице 3.4:

Склады вооружения	Потребители				Запасы
	10		3		10
Потребности	10		0		10

Таблица 3.4

5. 
   В клетку (2, 1) ставим 10 единиц.
   

Далее согласно алгоритму, ищем элементы среди не вычеркнутых.

8	7	12	11
10	4	3	5
9	6	1	2

Таблица 3.5

Искомый элемент (3, 4) = 2, но так как ограничения выполнены, то в ячейку (3, 4) ставим 0.

Таким образом, получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

В таблице заполнено m + n – 1 = 6 клеток, следовательно, опорный план является невырожденным. Стоимость перевозок составляет: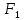

= 8*30 + 10*10 + 4*20 + 5*30 + 1*10 = 580 (y.e.)

8[30]	7	12	11
10[10]	4[20]	3	5[30]
9	6	1[10]	2[0]