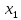методы оптимальных решений. МОР(5 задач). Решение Рассмотрим уравнения,, и и построим прямые, задающиеся этими уравнениями. 3
 Скачать 86.07 Kb. Скачать 86.07 Kb.
|
|
МОР Тимофеева А. Изобразите на плоскости множество точек, заданное системой ограничений: 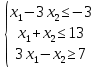 Если имеются угловые точки этого множества, найдите их координаты. Решение: Рассмотрим уравнения 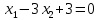 , , 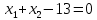 , и , и 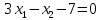 И построим прямые, задающиеся этими уравнениями. 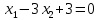 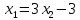
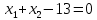 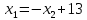
Построим:  На графике видно, что есть угловая точка – точка пересечения двух уравнений: 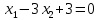 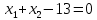 Определим ее координату, решив систему: 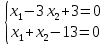 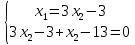 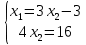 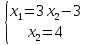  Таким образом, координаты угловой точки = (9; 4) Решите задачу ЛП графическим методом  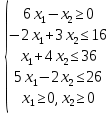 Решение: Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). 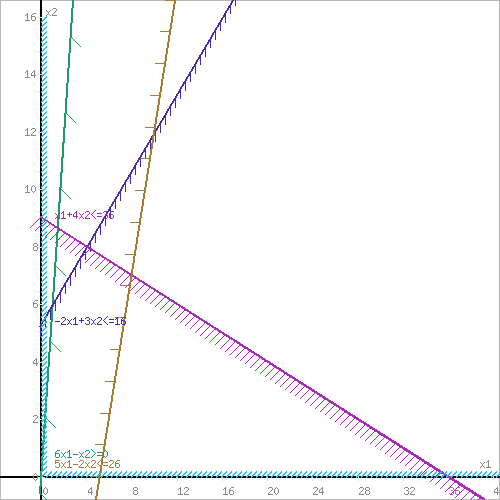 или 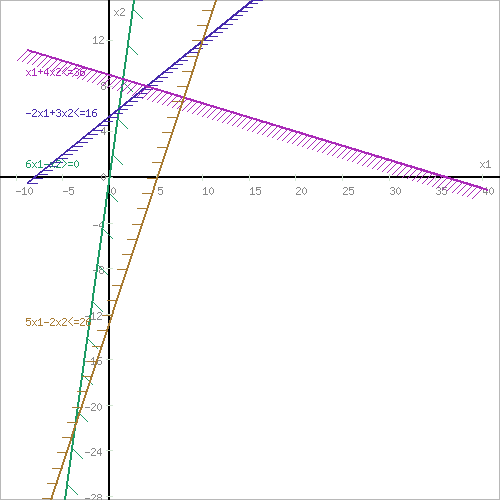 Шаг №2. Границы области допустимых решений. Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений.  Шаг №3. Рассмотрим целевую функцию задачи F = 2x1+6x2 → max. Построим прямую, отвечающую значению функции F = 2x1+6x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (2;6). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.  Прямая F(x) = const пересекает область в точке E. Так как точка E получена в результате пересечения прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых: x1+4x2=36 5x1-2x2=26 Решив систему уравнений, получим: x1 = 8, x2 = 7 Откуда найдем максимальное значение целевой функции: F(x) = 2∙8 + 6∙7 = 58 Дана задача ЛП: 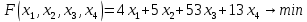 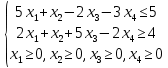 Составьте для этой задачи двойственную задачу и найдите решения обеих задач. Решение: Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим минимальное значение целевой функции F(X) = 4x1+5x2+53x3+13x4 при следующих условиях-ограничений. 5x1+x2-2x3-3x4≤5 2x1+x2+5x3-2x4≥4 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). 5x1+x2-2x3-3x4+x5 = 5 2x1+x2+5x3-2x4-x6 = 4 Введем искусственные переменные x: в 2-м равенстве вводим переменную x7; 5x1+x2-2x3-3x4+x5 = 5 2x1+x2+5x3-2x4-x6+x7 = 4 Для постановки задачи на минимум целевую функцию запишем так: F(X) = 4x1+5x2+53x3+13x4+Mx7 → min Из уравнений выражаем искусственные переменные: x7 = 4-2x1-x2-5x3+2x4+x6 которые подставим в целевую функцию: F(X) = 4x1 + 5x2 + 53x3 + 13x4 + M(4-2x1-x2-5x3+2x4+x6) → min или F(X) = (4-2M)x1+(5-M)x2+(53-5M)x3+(13+2M)x4+(M)x6+(4M) → min Решим систему уравнений относительно базисных переменных: x5, x7 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,0,5,0,4)
Переходим к основному алгоритму симплекс-метода. Итерация №0. Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент. Вычислим значения Di по строкам как частное от деления: bi / ai3 и из них выберем наименьшее: min (- , 4 : 5 ) = 4/5 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (5) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x7 в план 1 войдет переменная x3. Получаем новую симплекс-таблицу:
Итерация №1. Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент. Вычислим значения Di по строкам как частное от деления: bi / ai1 и из них выберем наименьшее: min (63/5 : 54/5 , 4/5 : 2/5 ) = 14/29 Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен (54/5) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 2 войдет переменная x1. Получаем новую симплекс-таблицу:
|