методы оптимальных решений. МОР(5 задач). Решение Рассмотрим уравнения,, и и построим прямые, задающиеся этими уравнениями. 3
 Скачать 86.07 Kb. Скачать 86.07 Kb.
|
|
Итерация №2. Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: min (14/29 : 7/29 , 10/29 : 3/29 ) = 31/3 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (3/29) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x3 в план 3 войдет переменная x2. Получаем новую симплекс-таблицу:
Конец итераций: индексная строка не содержит положительных элементов - найден оптимальный план Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Так как в оптимальном решении отсутствуют искусственные переменные (они равны нулю), то данное решение является допустимым. Оптимальный план можно записать так: x1 = 1/3, x2 = 31/3, x3 = 0, x4 = 0 F(X) = 4∙1/3 + 5∙31/3 + 53∙0 + 13∙0 = 18 Построим двойственную задачу по следующим правилам. 1. Количество переменных в двойственной задаче равно количеству неравенств в исходной. 2. Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной. 3. Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи. Столбец свободных членов исходной задачи является строкой коэффициентов для целевой функции двойственной. Целевая функция в одной задаче максимизируется, в другой минимизируется. Расширенная матрица A.
Транспонированная матрица AT.
Условиям неотрицательности переменных исходной задачи соответствуют неравенства-ограничения двойственной, направленные в другую сторону. И наоборот, неравенствам-ограничениям в исходной соответствуют условия неотрицательности в двойственной. Неравенства, соединенные стрелочками (↔), называются сопряженными. 5y1+2y2≤4 y1+y2≤5 -2y1+5y2≤53 -3y1-2y2≤13 5y1+4y2 → max y1 ≤ 0 y2 ≥ 0
Решение двойственной задачи дает оптимальную систему оценок ресурсов. Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи. y1=-2, y2=7 Это же решение можно получить, применив теоремы двойственности. Из теоремы двойственности следует, что Y = C∙A-1. Составим матрицу A из компонентов векторов, входящих в оптимальный базис. 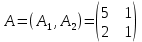 Определив обратную матрицу D = А-1 через алгебраические дополнения, получим: 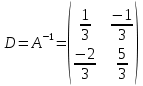 Как видно из последнего плана симплексной таблицы, обратная матрица A-1 расположена в столбцах дополнительных переменных. Тогда Y = C∙A-1 = 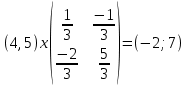 Оптимальный план двойственной задачи равен: y1 = -2, y2 = 7 Z(Y) = 5∙(-2)+4∙7 = 18 Критерий оптимальности полученного решения. Если существуют такие допустимые решения X и Y прямой и двойственной задач, для которых выполняется равенство целевых функций F(x) = Z(y), то эти решения X и Y являются оптимальными решениями прямой и двойственной задач соответственно. Экономический смысл всех переменных, участвующих в решении.
Определение дефицитных и недефицитных (избыточных) ресурсов. Вторая теорема двойственности. Подставим оптимальный план прямой задачи в систему ограниченной математической модели: 5∙1/3 + 1∙31/3 + (-2)∙0 + (-3)∙0 = 5 = 5 2∙1/3 + 1∙31/3 + 5∙0 + (-2)∙0 = 4 = 4 1-ое ограничение прямой задачи выполняется как равенство. Это означает, что 1-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y1 ≠ 0). 2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-й ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y2 ≠ 0). Двойственные оценки отражают сравнительную дефицитность различных видов ресурсов в отношении принятого в задаче показателя эффективности. Оценки показывают, какие ресурсы являются более дефицитными, (они будут иметь самые высокие оценки), какие менее дефицитными и какие совсем недефицитны (избыточны) - они будут равны нулю. Применяя теорему двойственности, получим решение двойственной задачи по известному решению исходной задачи. Найдем решение двойственной задачи у∙ воспользовавшись второй теоремой двойственности и известным оптимальным планом х∙. Поскольку x1>0, 1-е ограничение в двойственной задаче будет равенством. Поскольку x2>0, 2-е ограничение в двойственной задаче будет равенством. Таким образом, решение двойственной задачи сводится к решению уравнений при следующих условиях: -5y1+2y2 = 4 -y1+y2 = 5 -5y1+4y2 → max или -5y1+2y2 = 4 -y1+y2 = 5 -5y1+4y2 → max Обоснование эффективности оптимального плана. При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим: 5∙(-2) + 2∙7 = 4 = 4 1∙(-2) + 1∙7 = 5 = 5 -2∙(-2) + 5∙7 = 39 < 53 -3∙(-2) + (-2)∙7 = -8 < 13 1-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 1-й продукт экономически выгодно производить (убытки от производства этого вида продукции отсутствуют), а его использование предусмотрено оптимальным планом прямой задачи (x1>0). 2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 2-й продукт экономически выгодно производить (убытки от производства этого вида продукции отсутствуют), а его использование предусмотрено оптимальным планом прямой задачи (x2>0). 3-ое ограничение выполняется как строгое неравенство, т.е. продукцию 3-го вида производить экономически не выгодно. И действительно в оптимальном плане прямой задачи x3 = 0. При этом разница между ценами (39 - 53 = -14) показывает величину изменения целевой функции F(x) при введении дополнительной единицы xi. 4-ое ограничение выполняется как строгое неравенство, т.е. продукцию 4-го вида производить экономически не выгодно. И действительно в оптимальном плане прямой задачи x4 = 0. При этом разница между ценами (-8 - 13 = -21) показывает величину изменения целевой функции F(x) при введении дополнительной единицы xi. Решите задачу линейного программирования симплекс-методом 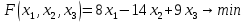 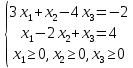 Решение: Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Поскольку в правой части присутствуют отрицательные значения, умножим соответствующие строки на (-1). Определим минимальное значение целевой функции F(X) = 8x1-14x2+9x3 при следующих условиях-ограничений. -3x1-x2+4x3=2 x1-2x2+x3=4 Расширенная матрица системы ограничений-равенств данной задачи: 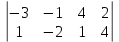 Приведем систему к единичной матрице методом жордановских преобразований. 1. В качестве базовой переменной можно выбрать x2. Разрешающий элемент РЭ=-1. Строка, соответствующая переменной x1, получена в результате деления всех элементов строки x2 на разрешающий элемент РЭ=-1. На месте разрешающего элемента получаем 1. В остальных клетках столбца x1 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А∙В)/РЭ СТЭ - элемент старого плана, РЭ - разрешающий элемент (-1), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
Получаем новую матрицу:
2. В качестве базовой переменной можно выбрать x3. Разрешающий элемент РЭ=-7. Строка, соответствующая переменной x2, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=-7. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
Получаем новую матрицу:
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (2,3). Выразим базисные переменные через остальные: x2 = x1-2 x3 = x1 Подставим их в целевую функцию: F(X) = 8x1-14(x1-2)+9(x1) или F(X) = 3x1+28 Среди свободных членов bi имеются отрицательные значения, следовательно, полученный базисный план не является опорным. Вместо переменной x2 следует ввести переменную x1. Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Представим расчет каждого элемента в виде таблицы:
Выразим базисные переменные через остальные: x1 = x2+2 x3 = x2+2 Подставим их в целевую функцию: F(X) = 8(x2+2)-14x2+9(x2+2) или F(X) = 3x2+34 x1-x2=2 -x2+x3=2 При вычислениях значение Fc = 34 временно не учитываем. Решим систему уравнений относительно базисных переменных: x1, x3 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (2,0,2)
Переходим к основному алгоритму симплекс-метода. Конец итераций: индексная строка не содержит положительных элементов - найден оптимальный план Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
