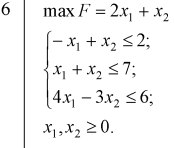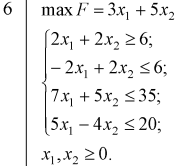КМ-2. Отчет по выполненной работы км студент иэозс6621 Хадри М. группа подпись фамилия и инициалы

• Название: Отчет по выполненной работы км студент иэозс6621 Хадри М. группа подпись фамилия и инициалы
• Дата: 29.04.2023
• Размер: 0.61 Mb.
• Имя файла: КМ-2.docx
• Тип: Отчет; #1097934

М ИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Национальный исследовательский университет «МЭИ»

Институт	ИНЭИ
Кафедра	БИТ

«ИССЛЕДОВАНИЕ ОПЕРАЦИЙ И МЕТОДЫ ОПТИМИЗАЦИИ»

ОТЧЕТ ПО ВЫПОЛНЕННОЙ РАБОТЫ КМ-2.

Студент

ИЭозс-66-21 Хадри М.

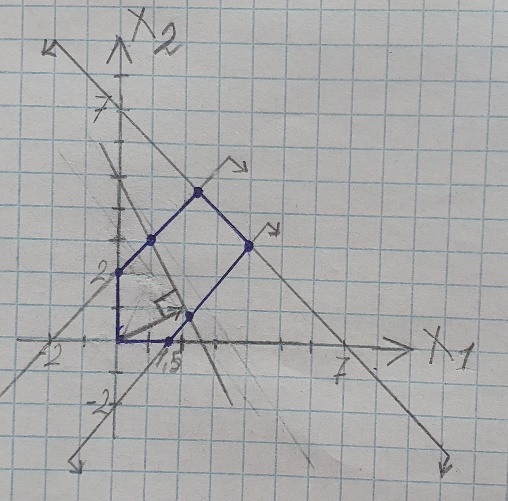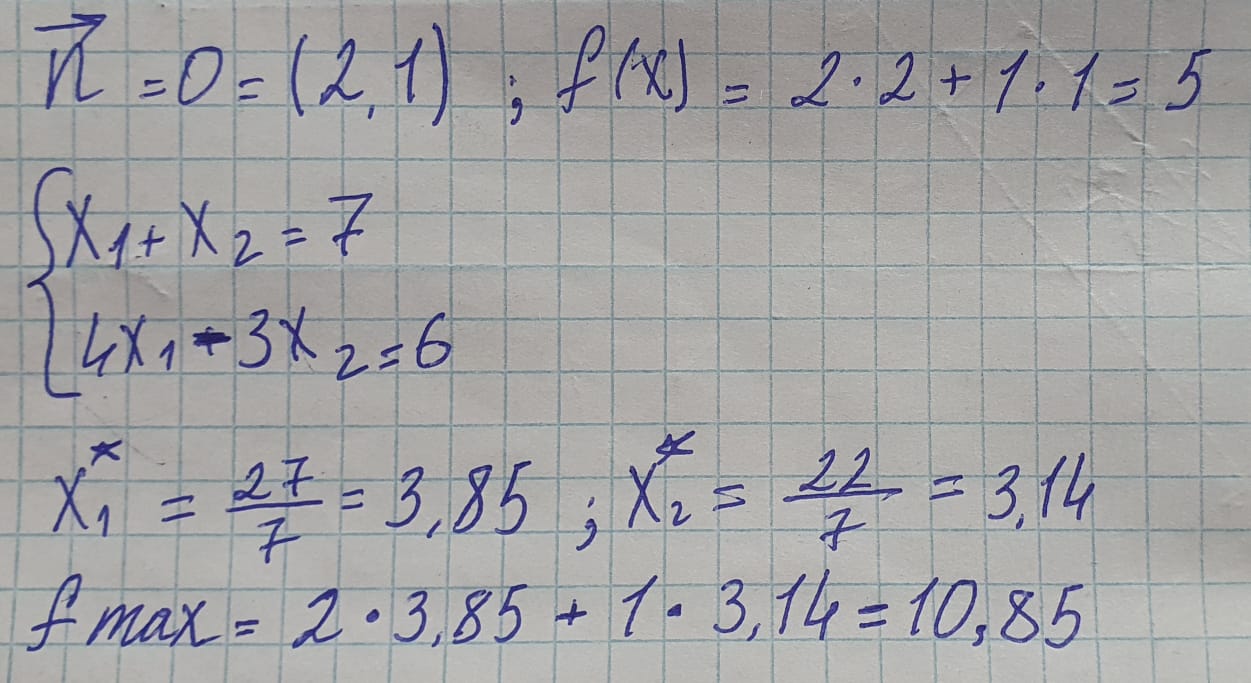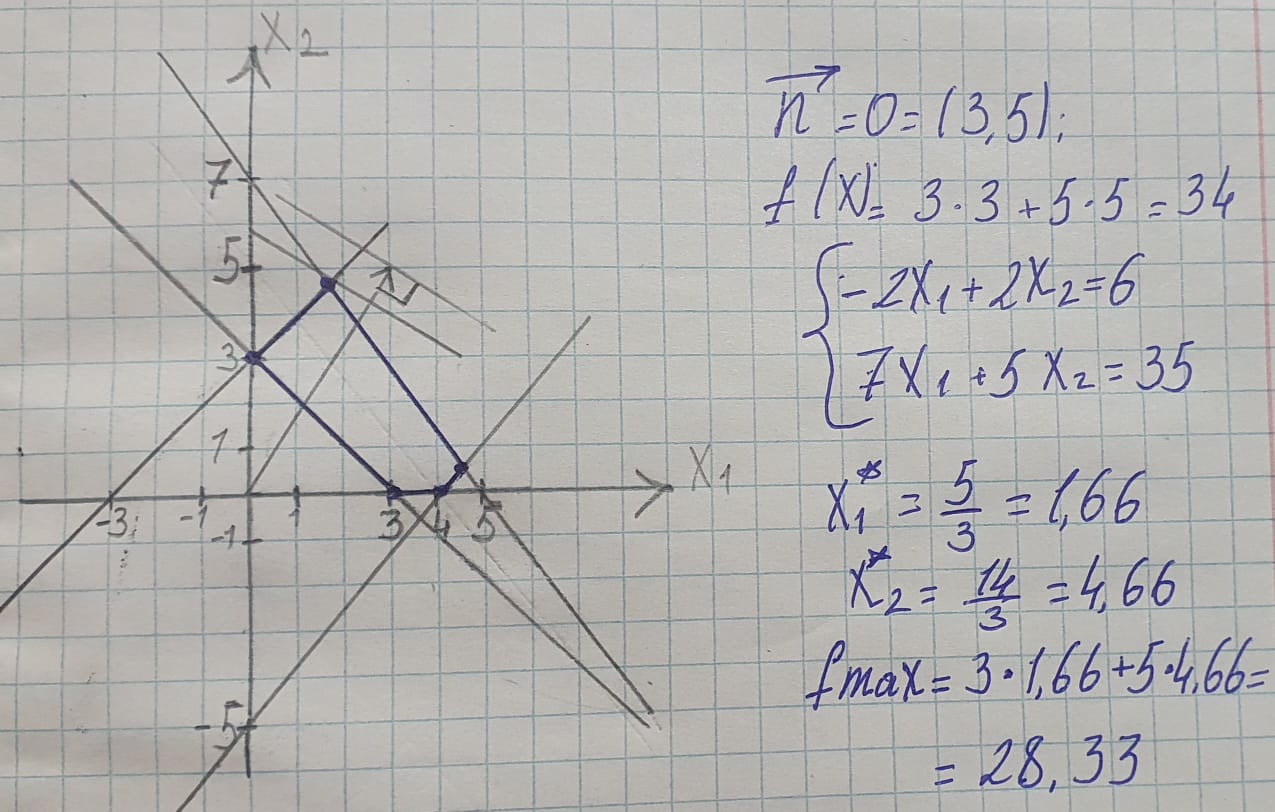группа подпись фамилия и инициалы Москва 2023 Цель работы Изучение современных программных средств решения задачи линейного программирования; практическое решение задач линейного программирования графическим методом, симплекс-методом и средствами программы Microsoft Excel; программная реализация симплекс-метода на языке программирования высокого уровня. Исходные значения линейного программирования

Графическое решение задач

Фрагменты рабочих листов с Excel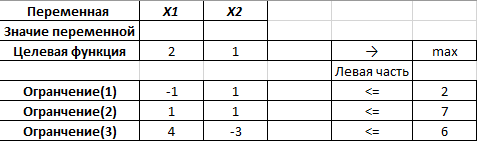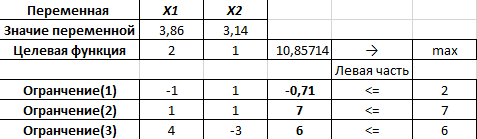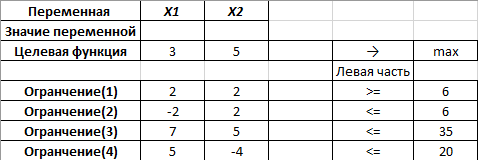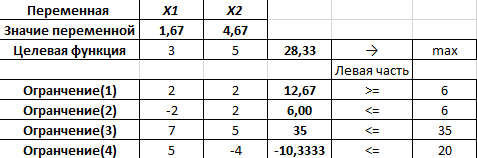









Решение табличным симплекс-методом

В 1-м неравенстве смысла (≤) вводим базисную переменную x4 . В 2-м неравенстве смысла (≤) вводим базисную переменную x5 . В 3-м неравенстве смысла (≤) вводим базисную переменную x6 .

2x1 + 7x2 + 6x3 + 1x4 + 0x5 + 0x6 = 10

-1x1 + 6x2 + 5x3 + 0x4 + 1x5 + 0x6 = 8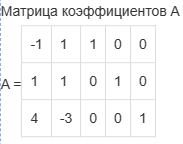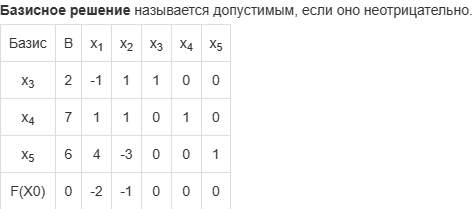

4x1 + 0x2 + 1x3 + 0x4 + 0x5 + 1x6 = 12

Итерация №0.

1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x2 , так как это наибольший коэффициент по модулю.

3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: min (10 : 7 , 8 : 6 , - ) = 11 /3 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (6) и находится на пересечении ведущего столбца и ведущей строки.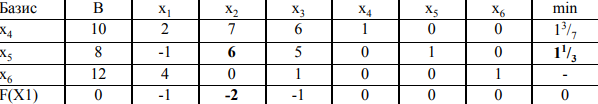



4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 1 войдет переменная x2 .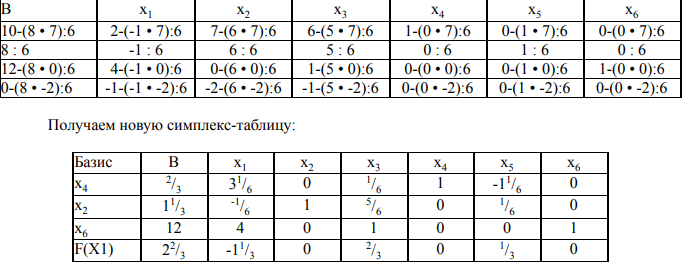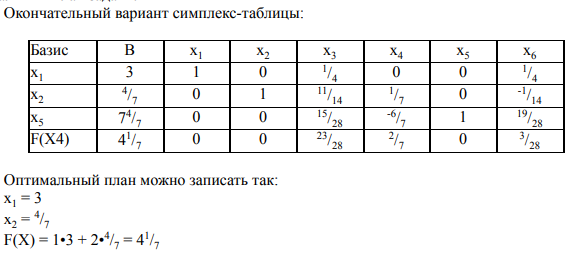





Схема алгоритма симплекс- метода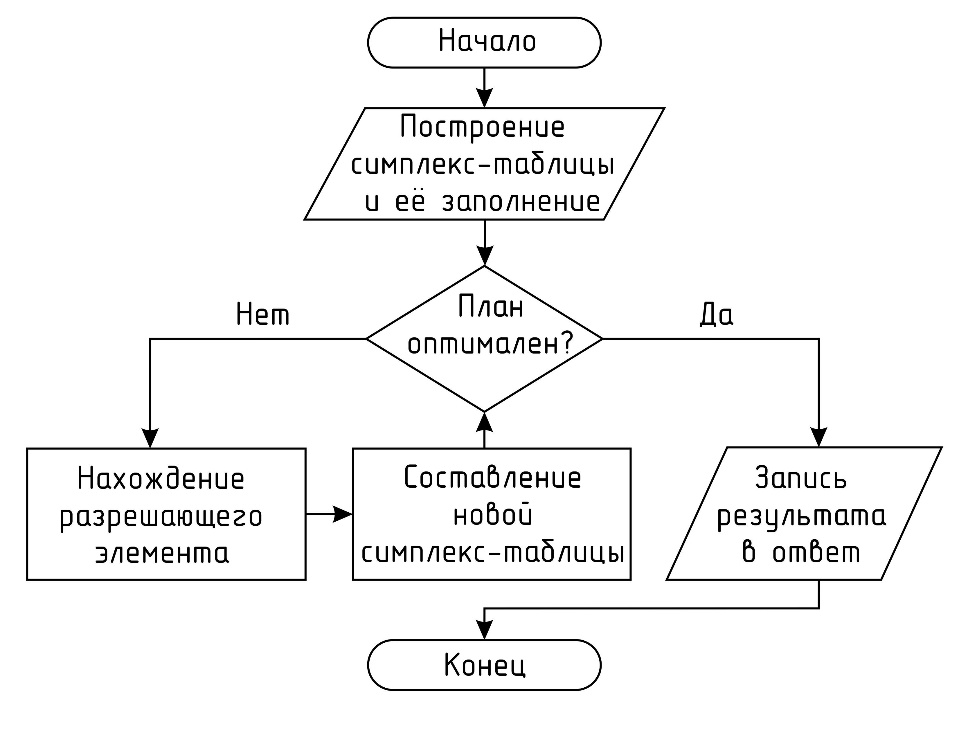



Анализ выполненной работы

Решая, задачи не сколько способом, я считаю, что удобнее всего пользоваться симплекс-методом для решения подобных задач. Графические решения и Excel «Поиск решения» дали абсолютно одинаковые результаты, что доказывает их точности в решения подобных задач. Также считаю, что «Поиск решения» в Excel удобен, тем что он автоматически создаёт несколько типов отчётности (Отчёт о результатах, о пределах и об устойчивости)