Решение военно-прикладных задач численными методами линейного программирования. Решение_военно-прикладных_задач_численными_методами_линейного_пр. Графоаналитический метод. Задача 1
 Скачать 47.98 Kb. Скачать 47.98 Kb.
|
|
Таблица 3.6 В) Проверим полученный план на оптимальность методом потенциалов. Для этого заполним таблицу 3.7:
Таблица 3.7 Составим системы уравнений вида 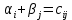 (только для занятых клеток): (только для занятых клеток):Положим, что 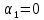 , получим , получим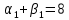  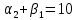 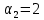 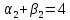 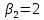 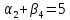 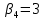  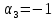  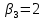 Оценим разности 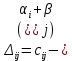 , (для свободный клеток) , (для свободный клеток)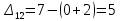 , ,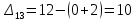 , ,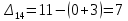 , ,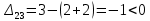 , ,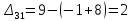 , ,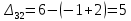 . .Так как в оценках разности есть отрицательные значения, то данный план не является оптимальным. Перераспределим перевозки грузов по циклу одной из клеток, имеющих отрицательную оценку, например, по циклу (2,3). Циклом в таблице условий транспортной задачи называется ломанная линия, вершины которой расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в столбце, а другое – в строке. Теперь переходим к новому опорному плану, для этого необходимо переместить грузы в пределах клеток, связанных с данной свободной клеткой. Эти перемещения производят по следующим правилам: Каждой из клеток, связанных циклом с данной свободной клеткой, приписывают определенный знак, причем в свободной клетке – знак плюс, а всем остальным клеткам – поочередно знаки минус и плюс. В данную свободную клетку переносят меньшее из значений перевозок 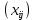 , стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитаются из чисел, стоящих в минусовых. Клетка, которая ранее была свободной, становится занятой, а минусовая клетка, в которой становится занятой, а минусовая клетка, в которой стояло минимальное из чисел , стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитаются из чисел, стоящих в минусовых. Клетка, которая ранее была свободной, становится занятой, а минусовая клетка, в которой становится занятой, а минусовая клетка, в которой стояло минимальное из чисел 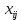 , считается свободной. , считается свободной.В результате указанных выше перемещений грузов в пределах клеток, связанных циклом (2,3 → 2,4 →3,4 → 3,3) с данной свободной клеткой, определяют новый опорный план транспортной задачи, при этом транспортные расходы составят 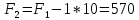 (у.е) (у.е)
Таблица 3.8 Полученный новый опорный план проверим на оптимальность. Для этого вновь находим потенциалы строк и столбцов, получим: 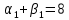  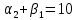 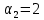 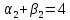 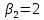 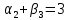 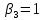 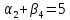 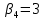  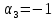 Оценим разности 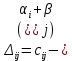 , (для свободный клеток) , (для свободный клеток)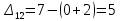 , ,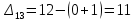 , ,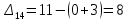 , ,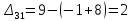 , ,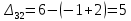 , ,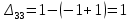 . .Так как в оценках разности присутствуют только положительные значения, то данный план является оптимальным. Ответ: 30 0 0 0 10 20 10 20 - матрица перевозок грузов; 0 0 0 10 В пункт  необходимо перебросить 30 ед. груза из необходимо перебросить 30 ед. груза из 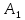 и 10 ед. груза из и 10 ед. груза из 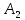 ; ;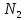 – 20 ед. груза из – 20 ед. груза из 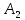 ; ;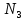 – 10 ед. груза из – 10 ед. груза из 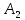 ; ;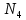 – 20 ед. груза из – 20 ед. груза из 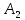 и 10 ед. груза и 10 ед. груза 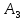 ; ;При этом затраты на перевозку составят 570 условных денежных единиц. Вывод. Задача линейного программирования состоит в том, чтобы максимизировать или минимизировать некоторые линейные функционалы на многомерном пространстве при заданных линейный ограничениях. Математическое программирование является одним из разделов науки об исследовании операций. СОДЕРЖАНИЕ Ввод…………………………………………………………………..2 Графоаналитический метод. Задача №1……………………….…..3-6 Симплекс-Метод. Задача №2……………………...………………..7-12 Решение транспортной задачи. Задача №3.……………….………13-19 Вывод……………………………………….………………………..20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 2
2