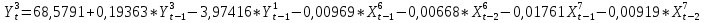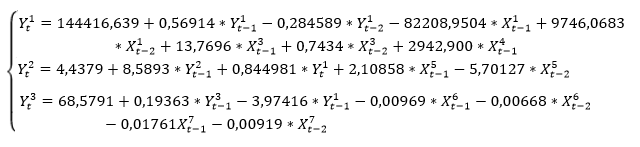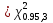
Коэффициенты являются значимыми. Параметр отражает зависимость от двух прошлых периодов.
Таблица 2.48- Коэффициенты автокорреляции переменной (Х7)
Х7t
|
0,843900966
|
0,851030802
|
0,854296336
|
0,854574819
|
0,852174839
|
870,52
|
864,13
|
852,16
|
834,45
|
821,52
|
763,10
|
864,13
|
852,16
|
834,45
|
821,52
|
763,10
|
761,49
|
852,16
|
834,45
|
821,52
|
763,10
|
761,49
|
199,40
|
834,45
|
821,52
|
763,10
|
761,49
|
199,40
|
179,91
|
821,52
|
763,10
|
761,49
|
199,40
|
179,91
|
520,83
|
763,10
|
761,49
|
199,40
|
179,91
|
520,83
|
853,44
|
761,49
|
199,40
|
179,91
|
520,83
|
853,44
|
927,05
|
199,40
|
179,91
|
520,83
|
853,44
|
927,05
|
763,36
|
179,91
|
520,83
|
853,44
|
927,05
|
763,36
|
730,76
|
520,83
|
853,44
|
927,05
|
763,36
|
730,76
|
637,01
|
853,44
|
927,05
|
763,36
|
730,76
|
637,01
|
512,37
|
927,05
|
763,36
|
730,76
|
637,01
|
512,37
|
422,86
|
763,36
|
730,76
|
637,01
|
512,37
|
422,86
|
433,35
|
730,76
|
637,01
|
512,37
|
422,86
|
433,35
|
134,58
|
637,01
|
512,37
|
422,86
|
433,35
|
134,58
|
164,76
|
512,37
|
422,86
|
433,35
|
134,58
|
164,76
|
154,12
|
422,86
|
433,35
|
134,58
|
164,76
|
154,12
|
142,12
|
433,35
|
134,58
|
164,76
|
154,12
|
142,12
|
135,75
|
134,58
|
164,76
|
154,12
|
142,12
|
135,75
|
132,99
|
164,76
|
154,12
|
142,12
|
135,75
|
132,99
|
0,0
|
154,12
|
142,12
|
135,75
|
132,99
|
0,0
|
0,0
|
142,12
|
135,75
|
132,99
|
0,0
|
0,0
|
0,0
|
135,75
|
132,99
|
0,0
|
0,0
|
0,0
|
0,0
|
132,99
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
Так как более точной является Q-статистика Льюнга-Бокса, для анализа она является более предпочтительной. Анализ автокорреляции в программе Statistica помимо коэффициентов автокорреляции автоматически рассчитывает Q-статистику Льюнга-Бокса и значимость для каждого коэффициента. Проверка значимости по Q-статистике Льюнга-Бокса равна 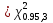
Коэффициенты являются значимыми. Параметр отражает зависимость от двух прошлых периодов.
8. Построит ADL- модель
С учетом результатов предшествующих анализов, ADL-модель принимает вид:
Для 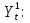
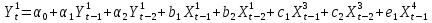
Для 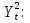
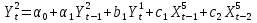
Для 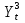
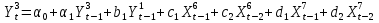
9. Решить построенную модель регрессии для показателей. Найти коэффициенты модели, используя регрессионный анализ. Написать уравнение модели с найденными коэффициентами.
Таблица 2.49 – Регрессионная статистика для У1
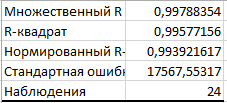
Таблица 2.50 – Дисперсионный анализ для У1

Таблица 2.51 – Коэффициенты регрессии для У1
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95.0%
|
Верхние 95.0%
|
Y-пересечение
|
144416,6391
|
17534,73157
|
8,236033642
|
3,79509E-07
|
107244,669
|
181588,6093
|
107244,669
|
181588,6093
|
Переменная X 1
|
0,569142879
|
0,223393726
|
2,547712007
|
0,021502483
|
0,095569338
|
1,04271642
|
0,095569338
|
1,04271642
|
Переменная X 2
|
-0,284589332
|
0,170849128
|
-1,665734764
|
0,11522092
|
-0,646773301
|
0,077594638
|
-0,646773301
|
0,077594638
|
Переменная X 3
|
-82208,95044
|
34798,48018
|
-2,362429337
|
0,031159428
|
-155978,4325
|
-8439,468395
|
-155978,4325
|
-8439,468395
|
Переменная X 4
|
9746,068354
|
5730,378288
|
1,700772246
|
0,108336527
|
-2401,790865
|
21893,92757
|
-2401,790865
|
21893,92757
|
Переменная X 5
|
13,76968175
|
3,316926855
|
4,151337172
|
0,000751227
|
6,738110979
|
20,80125252
|
6,738110979
|
20,80125252
|
Переменная X 6
|
0,743448374
|
5,465165463
|
0,13603401
|
0,893491249
|
-10,84218478
|
12,32908152
|
-10,84218478
|
12,32908152
|
Переменная X 7
|
2942,900395
|
1575,90374
|
1,867436646
|
0,080270404
|
-397,8662729
|
6283,667063
|
-397,8662729
|
6283,667063
|
Согласно результатам, уравнение записывается:
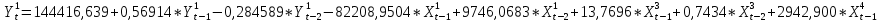
Таблица 2.52 – Регрессионная статистика для У2
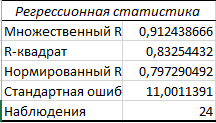
Таблица 2.53 – Дисперсионный анализ для У2

Таблица 2.54 – Коэффициенты регрессии для У2
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95.0%
|
Верхние 95.0%
|
Y-пересечение
|
4,437903197
|
18,92701794
|
0,234474507
|
0,817124832
|
-35,17680053
|
44,05260693
|
-35,17680053
|
44,05260693
|
Переменная X 1
|
0,844981888
|
0,137905011
|
6,127274731
|
6,8604E-06
|
0,556343384
|
1,133620393
|
0,556343384
|
1,133620393
|
Переменная X 2
|
2,10858E-05
|
0,000151908
|
0,13880641
|
0,891063798
|
-0,000296861
|
0,000339033
|
-0,000296861
|
0,000339033
|
Переменная X 3
|
-5,70127E-05
|
0,000114808
|
-0,496590052
|
0,625174734
|
-0,000297309
|
0,000183284
|
-0,000297309
|
0,000183284
|
Переменная X 4
|
4,68545E-05
|
9,0212E-05
|
0,519381716
|
0,60949241
|
-0,000141961
|
0,00023567
|
-0,000141961
|
0,00023567
|
Согласно результатам, уравнение записывается:
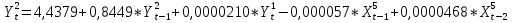
Таблица 2.55 – Регрессионная статистика для У3
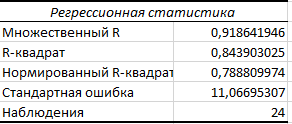
Таблица 2.56 – Дисперсионный анализ для У3

Таблица 2.57 – Коэффициенты регрессии для У3
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95.0%
|
Верхние 95.0%
|
Y-пересечение
|
68,57917554
|
10,11381189
|
6,780744621
|
3,20789E-06
|
47,24089787
|
89,91745322
|
47,24089787
|
89,91745322
|
Переменная X 1
|
0,193631567
|
0,13425984
|
1,442215082
|
0,167412286
|
-0,089631933
|
0,476895067
|
-0,089631933
|
0,476895067
|
Переменная X 2
|
-3,97417E-06
|
2,28069E-05
|
-0,174253071
|
0,863724873
|
-5,20925E-05
|
4,41441E-05
|
-5,20925E-05
|
4,41441E-05
|
Переменная X 3
|
-0,009697459
|
0,004605503
|
-2,105624212
|
0,050407827
|
-0,019414222
|
1,93033E-05
|
-0,019414222
|
1,93033E-05
|
Переменная X 4
|
-0,006686617
|
0,005438147
|
-1,229576413
|
0,235602375
|
-0,018160105
|
0,00478687
|
-0,018160105
|
0,00478687
|
Переменная X 5
|
-0,017619021
|
0,01989974
|
-0,885389518
|
0,388298906
|
-0,059603803
|
0,02436576
|
-0,059603803
|
0,02436576
|
Переменная X 6
|
-0,009196315
|
0,017794379
|
-0,516810116
|
0,611946892
|
-0,046739174
|
0,028346543
|
-0,046739174
|
0,028346543
|
Согласно результатам, уравнение записывается:
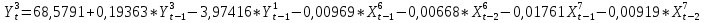
10. Проверим модель на достоверность с помощью F-критерия Фишера и коэффициента детерминации. По таблице дисперсионного анализа делаем вывод, что Fрасч ≥ Fтабл, построенное уравнение соответствует данным. Коэффициент детерминации (R2) больше 0,7, следовательно, построенная модель значима.
На основе полученных результатов анализа составим таблицу взаимозависимости эндогенных и экзогенных переменных модели.
Запишем модель в общем виде:
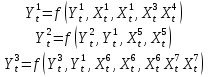 (8) (8)
Запишем модель в виде системы уравнений:
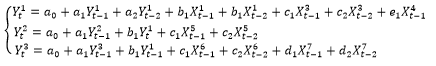 (9) (9)
С учетом найденных коэффициентов, модель принимает вид:
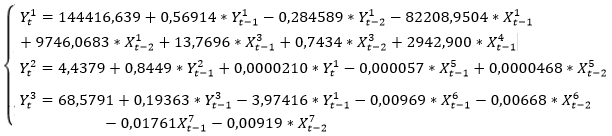
Далее определим идентифицируемость модели, чтобы выбрать приемлемый метод МНК. Данная модель сверхидентифицируемая (D+1 > Н), где Н – число эндогенных переменных в i-ом уравнении системы; D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Следует применить метод ДМНК для решения системы.
Рассчитаем теоретические значения эндогенных переменных путем подстановки экзогенных параметров в уравнения. Затем проводим ДМНК и находим новые коэффициенты.
Регрессионный анализ для уравнения 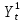 : :
-
Регрессионная статистика
|
Множественный R
|
1
|
R-квадрат
|
1
|
Нормированный R-квадрат
|
1
|
Стандартная ошибка
|
5,43314E-11
|
Наблюдения
|
24
|
Дисперсионный анализ для уравнения 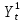 : :
Дисперсионный анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
7
|
1,16285E+12
|
1,66121E+11
|
5,62758E+31
|
6,577E-250
|
Остаток
|
16
|
4,72305E-20
|
2,9519E-21
|
|
|
Итого
|
23
|
1,16285E+12
|
|
|
|
Коэффициенты регрессии для уравнения 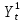 : :
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
144416,6391
|
5,42299E-11
|
2,66304E+15
|
1,3183E-238
|
144416,6391
|
144416,6391
|
144416,6391
|
144416,6391
|
Переменная X 1
|
0,569142879
|
6,90893E-16
|
8,23779E+14
|
1,8754E-230
|
0,569142879
|
0,569142879
|
0,569142879
|
0,569142879
|
Переменная X 2
|
-0,284589332
|
5,28388E-16
|
-5,386E+14
|
1,6819E-227
|
-0,284589332
|
-0,284589332
|
-0,284589332
|
-0,284589332
|
Переменная X 3
|
-82208,95044
|
1,07622E-10
|
-7,63869E+14
|
6,277E-230
|
-82208,95044
|
-82208,95044
|
-82208,95044
|
-82208,95044
|
Переменная X 4
|
9746,068354
|
1,77224E-11
|
5,49929E+14
|
1,2055E-227
|
9746,068354
|
9746,068354
|
9746,068354
|
9746,068354
|
Переменная X 5
|
13,76968175
|
1,02583E-14
|
1,3423E+15
|
7,5943E-234
|
13,76968175
|
13,76968175
|
13,76968175
|
13,76968175
|
Переменная X 6
|
0,743448374
|
1,69022E-14
|
4,39853E+13
|
4,2967E-210
|
0,743448374
|
0,743448374
|
0,743448374
|
0,743448374
|
Переменная X 7
|
2942,900395
|
4,87382E-12
|
6,03818E+14
|
2,7012E-228
|
2942,900395
|
2942,900395
|
2942,900395
|
2942,900395
|
Согласно результатам, уравнение записывается:
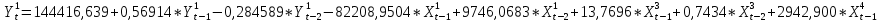
Регрессионный анализ для уравнения 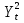 : :
Регрессионная статистика
|
Множественный R
|
1
|
R-квадрат
|
1
|
Нормированный R-квадрат
|
1
|
Стандартная ошибка
|
7,04834E-15
|
Наблюдения
|
24
|
Дисперсионный анализ для уравнения 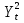 : :
Дисперсионный анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
5
|
11432,37313
|
2286,474626
|
4,60249E+31
|
2,7034E-279
|
Остаток
|
18
|
8,94223E-28
|
4,96791E-29
|
|
|
Итого
|
23
|
11432,37313
|
|
|
|
Коэффициенты регрессии для уравнения 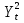 : :
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
4,437903197
|
1,21439E-14
|
3,65443E+14
|
2,7226E-252
|
4,437903197
|
4,437903197
|
4,437903197
|
4,437903197
|
Переменная X 1
|
8,58937E-17
|
1,46985E-16
|
0,584371434
|
0,566223283
|
-2,2291E-16
|
3,94697E-16
|
-2,2291E-16
|
3,94697E-16
|
Переменная X 2
|
0,844981888
|
1,52421E-16
|
5,54375E+15
|
1,504E-273
|
0,844981888
|
0,844981888
|
0,844981888
|
0,844981888
|
Переменная X 3
|
2,10858E-05
|
9,73755E-20
|
2,16541E+14
|
3,3574E-248
|
2,10858E-05
|
2,10858E-05
|
2,10858E-05
|
2,10858E-05
|
Переменная X 4
|
-5,70127E-05
|
7,40326E-20
|
-7,70103E+14
|
4,0537E-258
|
-5,70127E-05
|
-5,70127E-05
|
-5,70127E-05
|
-5,70127E-05
|
Согласно данным уравнение записывается:
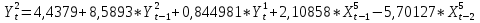
Регрессионный анализ для уравнения 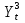 : :
|
|
Регрессионная статистика
|
Множественный R
|
1
|
R-квадрат
|
1
|
Нормированный R-квадрат
|
1
|
Стандартная ошибка
|
9,37486E-15
|
Наблюдения
|
24
|
Дисперсионный анализ для уравнения 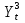 : :
Дисперсионный анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
6
|
11256,49321
|
1876,082201
|
2,13463E+31
|
1,7506E-261
|
Остаток
|
17
|
1,4941E-27
|
8,7888E-29
|
|
|
Итого
|
23
|
11256,49321
|
|
|
|
Коэффициенты регрессии для уравнения 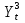 : :
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
68,57917554
|
8,56745E-15
|
8,00462E+15
|
2,4119E-261
|
68,57917554
|
68,57917554
|
68,57917554
|
68,57917554
|
Переменная X 1
|
0,193631567
|
1,13732E-16
|
1,70252E+15
|
6,4649E-250
|
0,193631567
|
0,193631567
|
0,193631567
|
0,193631567
|
Переменная X 2
|
-3,97417E-06
|
1,93198E-20
|
-2,05704E+14
|
2,5942E-234
|
-3,97417E-06
|
-3,97417E-06
|
-3,97417E-06
|
-3,97417E-06
|
Переменная X 3
|
-0,009697459
|
3,90134E-18
|
-2,48567E+15
|
1,039E-252
|
-0,009697459
|
-0,009697459
|
-0,009697459
|
-0,009697459
|
Переменная X 4
|
-0,006686617
|
4,60668E-18
|
-1,45151E+15
|
9,7326E-249
|
-0,006686617
|
-0,006686617
|
-0,006686617
|
-0,006686617
|
Переменная X 5
|
-0,017619021
|
1,68572E-17
|
-1,0452E+15
|
2,587E-246
|
-0,017619021
|
-0,017619021
|
-0,017619021
|
-0,017619021
|
Переменная X 6
|
-0,009196315
|
1,50737E-17
|
-6,1009E+14
|
2,4403E-242
|
-0,009196315
|
-0,009196315
|
-0,009196315
|
-0,009196315
|
Согласно данным уравнение записывается
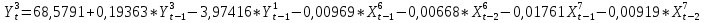
Подставим новые коэффициенты, найденные Двойным МНК, в каждое уравнение системы:
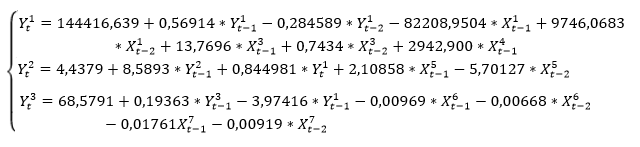
Коэффициенты детерминации всех уравнений системы больше 0,7 и fрасчетное больше табличного следовательно можно сделать вывод о соответствие модели данным.
Далее решим систему с помощью программы Excel и построим прогноз на 2018 год для каждой эндогенной переменной.
Таблица 2..58. Прогноз модели
1996
|
18972,55714
|
137,54846
|
603,39456
|
1997
|
19472,56837
|
186,18574
|
752,53279
|
1998
|
19587,57825
|
227,82736
|
982,83572
|
1999
|
24123,58248
|
256,08671
|
879,25732
|
2000
|
26635,59468
|
241,62103
|
934,96582
|
2001
|
15993,60742
|
257,75215
|
1082,9667
|
2002
|
15552,61423
|
297,65247
|
1224,2934
|
2003
|
21293,61856
|
347,85294
|
1227,2472
|
2004
|
53886,63785
|
410,15837
|
1561,7887
|
2005
|
50091,64857
|
481,08937
|
1938,7482
|
2006
|
50091,6548
|
767,32456
|
2347,7569
|
2007
|
48031,67248
|
890,45395
|
2772,7167
|
2008
|
62895,68856
|
1072,8752
|
3391,0124
|
2009
|
65326,68975
|
1176,4572
|
4182,7052
|
2010
|
40066,69729
|
1241,8762
|
4863,2167
|
2011
|
48181,69854
|
1397,5123
|
5689,1863
|
2012
|
55995,71143
|
1414,8697
|
6532,4834
|
2013
|
61579,72975
|
1735,4687
|
6852,6712
|
2014
|
75526,72786
|
1849,7286
|
7127,8486
|
2015
|
95594,74199
|
1975,4231
|
8524,2067
|
2016
|
114999,7576
|
1776,6712
|
8375,2631
|
2017
|
125157,7456
|
1687,3752
|
12441,641
|
2018
|
139831,308
|
1852,4587
|
13257,623
|
Рис.2.1 Прогноз на 2018год
ВВП по достижению к 2018 году продолжит расти. Это связанно с важным значением территории области для РФ. Инвестиции и развития региона являются одной из первоочередных целей развития стран Арктики
Рис.2.2 Прогноз на 2018 год
После небольшого спада экспорт минеральных продуктов будет наращивать свои обороты. Архангельская область обладает богатыми залежами полезных ископаемых. Большое количество инвестиций в данную отрасль усилят позицию области по количеству экспорта минералов и его конкурентно-способности на рынке.
Рис.2.3 Прогноз на 2018 год
По прогнозам к 2018 году ЛПК должна совершить огромный скачок в развитии. Являясь одной из больших и популярных отраслей, на экспорте лесной промышленности строится большая часть экономики страны.
Вывод по проделанному анализу
Высокий уровень экспорта в регионе это показатель эффективного функционирования экономики. Экспортный потенциал для Архангельской области- очень актуальный показатель. Это связанно прежде всего с тем, что экспорт составляет огромную долю в внешнеторговом обороте. Продукция отраслей ЛПК является востребованной и конкурентно-способной на внешних рынках. По графикам и про прогнозам на текущий год видно, что при должных инвестициях и развития сфер региона, экспорт данной области будет на уровне достойным уровня стран запада.
|
 Скачать 1.08 Mb.
Скачать 1.08 Mb.
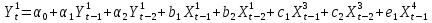
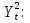
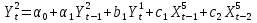
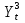
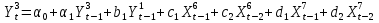


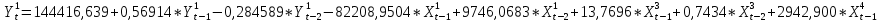


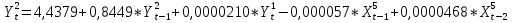


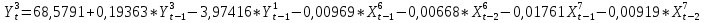
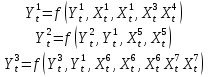 (8)
(8)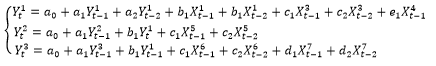 (9)
(9)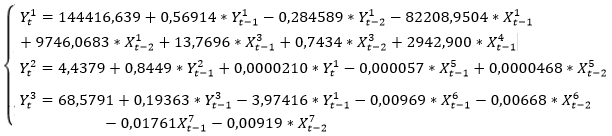
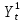 :
: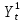 :
: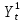 :
: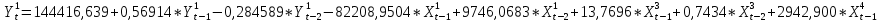
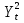 :
: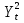 :
: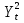 :
: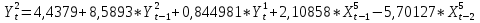
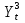 :
: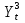 :
: :
: