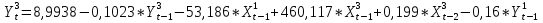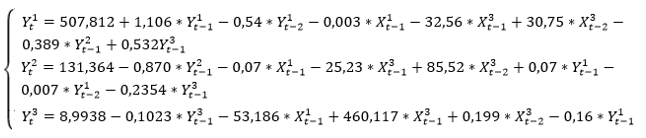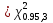
Коэффициенты являются значимыми. Параметр отражает зависимость от двух прошлых периодов.
8. Построит ADL- модель
С учетом результатов предшествующих анализов, ADL-модель принимает вид:
Для 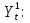
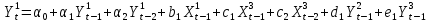
Для 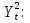
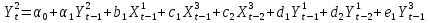
Для 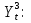
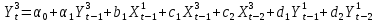
9. Решить построенную модель регрессии для показателей. Найти коэффициенты модели, используя регрессионный анализ. Написать уравнение модели с найденными коэффициентами.
Таблица 3.49 – Регрессионная статистика для У1
Регрессионная статистика
|
Множественный R
|
0,903771225
|
R-квадрат
|
0,816802427
|
Нормированный R-квадрат
|
0,759553185
|
Стандартная ошибка
|
705,3102657
|
Наблюдения
|
22
|
Таблица 3.50 – Дисперсионный анализ для У1
Дисперсионный анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
5
|
35487687,15
|
7097537,431
|
14,2674803
|
2,05506E-05
|
Остаток
|
16
|
7959401,134
|
497462,5709
|
|
|
Итого
|
21
|
43447088,29
|
|
|
|
Таблица 3.51 – Коэффициенты регрессии для У1
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
724,9457873
|
318,019093
|
2,279566867
|
0,036688225
|
50,77542683
|
1399,116148
|
50,77542683
|
1399,116148
|
Переменная X 1
|
0,793487418
|
0,14426691
|
5,500134563
|
4,84422E-05
|
0,487655231
|
1,099319605
|
0,487655231
|
1,099319605
|
Переменная X 2
|
189,6456805
|
228,8944619
|
0,828528916
|
0,419559299
|
-295,5889022
|
674,8802631
|
-295,5889022
|
674,8802631
|
Переменная X 3
|
-142,8410975
|
283,8399955
|
-0,503245137
|
0,62164907
|
-744,5550082
|
458,8728132
|
-744,5550082
|
458,8728132
|
Переменная X 4
|
-1,279306926
|
0,625804763
|
-2,044258853
|
0,057747178
|
-2,605953759
|
0,047339906
|
-2,605953759
|
0,047339906
|
Переменная X 5
|
0,327735127
|
0,279844995
|
1,171130921
|
0,258692668
|
-0,265509761
|
0,920980015
|
-0,265509761
|
0,920980015
|
Согласно результатам, уравнение записывается:
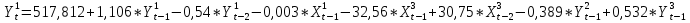
Таблица 3.52 – Регрессионная статистика для У2
Регрессионная статистика
|
Множественный R
|
0,76809322
|
R-квадрат
|
0,589967195
|
Нормированный R-квадрат
|
0,425954073
|
Стандартная ошибка
|
232,9377946
|
Наблюдения
|
22
|
Таблица 3.53 – Дисперсионный анализ для У2
Дисперсионный анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
6
|
1171063,478
|
195177,2463
|
3,597073131
|
0,020612409
|
Остаток
|
15
|
813900,2426
|
54260,01617
|
|
|
Итого
|
21
|
1984963,72
|
|
|
|
Таблица 3.54 – Коэффициенты регрессии для У2
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
131,3641421
|
116,8659224
|
1,124058574
|
0,279892965
|
-119,2883326
|
382,0166168
|
-119,2883326
|
382,0166168
|
Переменная X 1
|
0,87093778
|
0,129712487
|
6,714371146
|
9,87242E-06
|
0,592732165
|
1,149143396
|
0,592732165
|
1,149143396
|
Переменная X 2
|
-0,071995717
|
0,120710043
|
-0,596435182
|
0,56040573
|
-0,330893011
|
0,186901577
|
-0,330893011
|
0,186901577
|
Переменная X 3
|
-25,23932055
|
38,84668693
|
-0,649716168
|
0,526393029
|
-108,5571776
|
58,07853645
|
-108,5571776
|
58,07853645
|
Переменная X 4
|
85,52293154
|
47,67732803
|
1,793786168
|
0,094467369
|
-16,73476694
|
187,78063
|
-16,73476694
|
187,78063
|
Переменная X 5
|
0,078091339
|
0,043904638
|
1,778658071
|
0,09700988
|
-0,016074745
|
0,172257423
|
-0,016074745
|
0,172257423
|
Переменная X 6
|
-0,007068261
|
0,041495737
|
-0,170337038
|
0,867182185
|
-0,096067765
|
0,081931243
|
-0,096067765
|
0,081931243
|
Переменная X 7
|
-0,235483869
|
0,048676401
|
-4,837741968
|
0,00026324
|
-0,339884367
|
-0,131083372
|
-0,339884367
|
-0,131083372
|
Согласно результатам, уравнение записывается:
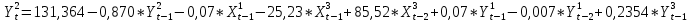
Таблица 3.55 – Регрессионная статистика для У3
Регрессионная статистика
|
Множественный R
|
0,77826879
|
R-квадрат
|
0,605702309
|
Нормированный R-квадрат
|
0,482484281
|
Стандартная ошибка
|
608,8433945
|
Наблюдения
|
22
|
Таблица 3.56 – Дисперсионный анализ для У3
Дисперсионный анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
5
|
9111002,714
|
1822200,543
|
4,915695517
|
0,006475007
|
Остаток
|
16
|
5931044,465
|
370690,2791
|
|
|
Итого
|
21
|
15042047,18
|
|
|
|
Таблица 3.57 – Коэффициенты регрессии для У3
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
8,993832524
|
606,9587768
|
0,014817864
|
0,988360688
|
-1277,701295
|
1295,68896
|
-1277,701295
|
1295,68896
|
Переменная X 1
|
-0,102372749
|
0,563986802
|
-0,181516214
|
0,858242001
|
-1,297971361
|
1,093225862
|
-1,297971361
|
1,093225862
|
Переменная X 2
|
-53,18694849
|
190,5893054
|
-0,279065755
|
0,783769273
|
-457,2182269
|
350,84433
|
-457,2182269
|
350,84433
|
Переменная X 3
|
460,117047
|
219,1100027
|
2,099936294
|
0,051946892
|
-4,375408796
|
924,6095028
|
-4,375408796
|
924,6095028
|
Переменная X 4
|
0,199257182
|
0,187179358
|
1,064525407
|
0,302892989
|
-0,197545331
|
0,596059696
|
-0,197545331
|
0,596059696
|
Переменная X 5
|
-0,163695401
|
0,19553159
|
-0,83718135
|
0,414820908
|
-0,578203856
|
0,250813054
|
-0,578203856
|
0,250813054
|
Согласно результатам, уравнение записывается:
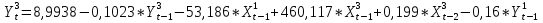
10. Проверим модель на достоверность с помощью F-критерия Фишера и коэффициента детерминации. По таблице дисперсионного анализа делаем вывод, что Fрасч ≥ Fтабл, построенное уравнение соответствует данным. Коэффициент детерминации (R2) больше 0,7, следовательно, построенная модель значима.
На основе полученных результатов анализа составим таблицу взаимозависимости эндогенных и экзогенных переменных модели.
Запишем модель в общем виде:
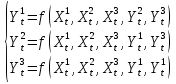 (8) (8)
Запишем модель в виде системы уравнений:
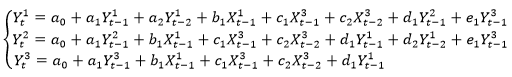 (9) (9)
С учетом найденных коэффициентов, модель принимает вид:
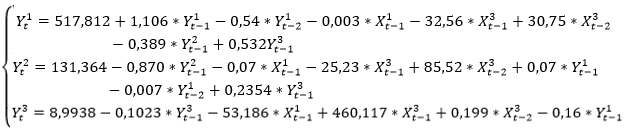
Далее определим идентифицируемость модели, чтобы выбрать приемлемый метод МНК.
Данная модель неидентифицируемая (D+1 < Н), где Н – число эндогенных переменных в i-ом уравнении системы; D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение. Следует применить метод ДМНК для решения системы.
Рассчитаем теоретические значения эндогенных переменных путем подстановки экзогенных параметров в уравнения. Затем проводим ДМНК и находим новые коэффициенты. Расчеты осуществляются в программе Excel.
Регрессионный анализ для уравнения 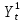 : :
Регрессионная статистика
|
Множественный R
|
1
|
R-квадрат
|
1
|
Нормированный R-квадрат
|
1
|
Стандартная ошибка
|
5,07298E-13
|
Наблюдения
|
22
|
Дисперсионный анализ для уравнения 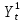 : :
Дисперсионный анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
7
|
35812028,19
|
5116004,027
|
1,98794E+31
|
7,0585E-216
|
Остаток
|
14
|
3,60292E-24
|
2,57351E-25
|
|
|
Итого
|
21
|
35812028,19
|
|
|
|
Коэффициенты регрессии для уравнения 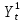 : :
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
507,8129549
|
5,06622E-13
|
1,00235E+15
|
2,1367E-203
|
507,8129549
|
507,8129549
|
507,8129549
|
507,8129549
|
Переменная X 1
|
1,106355502
|
1,9033E-16
|
5,81284E+15
|
4,3912E-214
|
1,106355502
|
1,106355502
|
1,106355502
|
1,106355502
|
Переменная X 2
|
-0,540438373
|
1,79887E-16
|
-3,00432E+15
|
4,5245E-210
|
-0,540438373
|
-0,540438373
|
-0,540438373
|
-0,540438373
|
Переменная X 3
|
-0,003879206
|
5,23286E-16
|
-7,41316E+12
|
1,4587E-173
|
-0,003879206
|
-0,003879206
|
-0,003879206
|
-0,003879206
|
Переменная X 4
|
32,56591751
|
1,68403E-13
|
1,93381E+14
|
2,1589E-193
|
32,56591751
|
32,56591751
|
32,56591751
|
32,56591751
|
Переменная X 5
|
30,75973781
|
2,06684E-13
|
1,48825E+14
|
8,4446E-192
|
30,75973781
|
30,75973781
|
30,75973781
|
30,75973781
|
Переменная X 6
|
-0,389307656
|
5,62313E-16
|
-6,92333E+14
|
3,7985E-201
|
-0,389307656
|
-0,389307656
|
-0,389307656
|
-0,389307656
|
Переменная X 7
|
0,532604765
|
2,11016E-16
|
2,52401E+15
|
5,1851E-209
|
0,532604765
|
0,532604765
|
0,532604765
|
0,532604765
|
Согласно результатам, уравнение записывается:
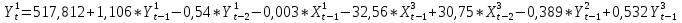
Регрессионный анализ для уравнения 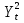 : :
Регрессионная статистика
|
Множественный R
|
1
|
R-квадрат
|
1
|
Нормированный R-квадрат
|
1
|
Стандартная ошибка
|
1,08459E-13
|
Наблюдения
|
22
|
Дисперсионный анализ для уравнения 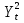 : :
Дисперсионный анализ
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
8
|
1592843,878
|
199105,4848
|
1,69259E+31
|
2,4491E-200
|
Остаток
|
13
|
1,52924E-25
|
1,17633E-26
|
|
|
Итого
|
21
|
1592843,878
|
|
|
|
Коэффициенты регрессии для уравнения 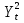 : :
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
131,3641421
|
1,13097E-13
|
1,16152E+15
|
5,3938E-190
|
131,3641421
|
131,3641421
|
131,3641421
|
131,3641421
|
Переменная X 1
|
3,12118E-16
|
2,47705E-16
|
1,260040544
|
0,229804936
|
-2,23015E-16
|
8,47251E-16
|
-2,23015E-16
|
8,47251E-16
|
Переменная X 2
|
0,87093778
|
2,46971E-16
|
3,52647E+15
|
2,8962E-196
|
0,87093778
|
0,87093778
|
0,87093778
|
0,87093778
|
Переменная X 3
|
-0,071995717
|
1,1329E-16
|
-6,35501E+14
|
1,3701E-186
|
-0,071995717
|
-0,071995717
|
-0,071995717
|
-0,071995717
|
Переменная X 4
|
-25,23932055
|
3,65429E-14
|
-6,90677E+14
|
4,6418E-187
|
-25,23932055
|
-25,23932055
|
-25,23932055
|
-25,23932055
|
Переменная X 5
|
85,52293154
|
4,90042E-14
|
1,74522E+15
|
2,7115E-192
|
85,52293154
|
85,52293154
|
85,52293154
|
85,52293154
|
Переменная X 6
|
0,078091339
|
4,50556E-17
|
1,73322E+15
|
2,9659E-192
|
0,078091339
|
0,078091339
|
0,078091339
|
0,078091339
|
Переменная X 7
|
-0,007068261
|
3,84992E-17
|
-1,83595E+14
|
1,403E-179
|
-0,007068261
|
-0,007068261
|
-0,007068261
|
-0,007068261
|
Переменная X 8
|
-0,235483869
|
7,37412E-17
|
-3,19338E+15
|
1,0519E-195
|
-0,235483869
|
-0,235483869
|
-0,235483869
|
-0,235483869
|
Согласно результатам, уравнение записывается:
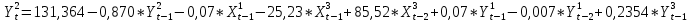
Регрессионный анализ для уравнения 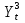 : :
Регрессионная статистика
|
Множественный R
|
0,77826879
|
R-квадрат
|
0,605702309
|
Нормированный R-квадрат
|
0,482484281
|
Стандартная ошибка
|
608,8433945
|
Наблюдения
|
22
|
Дисперсионный анализ для уравнения 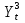 : :
Дисперсионный анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
Регрессия
|
5
|
9111002,714
|
1822200,543
|
4,915695517
|
0,006475007
|
Остаток
|
16
|
5931044,465
|
370690,2791
|
|
|
Итого
|
21
|
15042047,18
|
|
|
|
Коэффициенты регрессии для уравнения 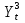 : :
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
Y-пересечение
|
8,993832524
|
606,9587768
|
0,014817864
|
0,988360688
|
-1277,701295
|
1295,68896
|
-1277,701295
|
1295,68896
|
Переменная X 1
|
-0,102372749
|
0,563986802
|
-0,181516214
|
0,858242001
|
-1,297971361
|
1,093225862
|
-1,297971361
|
1,093225862
|
Переменная X 2
|
-53,18694849
|
190,5893054
|
-0,279065755
|
0,783769273
|
-457,2182269
|
350,84433
|
-457,2182269
|
350,84433
|
Переменная X 3
|
460,117047
|
219,1100027
|
2,099936294
|
0,051946892
|
-4,375408796
|
924,6095028
|
-4,375408796
|
924,6095028
|
Переменная X 4
|
0,199257182
|
0,187179358
|
1,064525407
|
0,302892989
|
-0,197545331
|
0,596059696
|
-0,197545331
|
0,596059696
|
Переменная X 5
|
-0,163695401
|
0,19553159
|
-0,83718135
|
0,414820908
|
-0,578203856
|
0,250813054
|
-0,578203856
|
0,250813054
|
Согласно результатам, уравнение записывается:
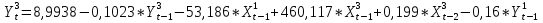
Подставим новые коэффициенты, найденные Двойным МНК, в каждое уравнение системы
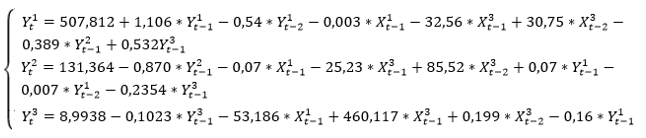
Коэффициенты детерминации всех уравнений системы больше 0,7 и fрасчетное больше табличного следовательно можно сделать вывод о соответствие модели данным.
Далее решим систему с помощью программы Excel и построим прогноз на 2018 год для каждой эндогенной переменной.
Таблица 3.3.58. Прогноз на 2018 год
Год
|
У1-модель
|
У2 модель
|
У3 модель
|
1996
|
18972,79125
|
0,489632144
|
6497,389742
|
1997
|
19472,48534
|
0,497658123
|
6528,558741
|
1998
|
19587,51387
|
0,526238779
|
6872,652149
|
1999
|
24123,52478
|
0,529874523
|
6941,514734
|
2000
|
26635,61589
|
0,536729125
|
7077,442384
|
2001
|
15933,81812
|
0,540401396
|
13223,10869
|
2002
|
15552,52663
|
0,546477387
|
20630,08508
|
2003
|
21293,40486
|
0,554347907
|
25000,45093
|
2004
|
53886,93563
|
0,561126158
|
38928,82444
|
2005
|
50091,09834
|
0,569435098
|
52096,2039
|
2006
|
48031,83995
|
0,586337277
|
73317,47364
|
2007
|
62895,02584
|
0,58695418
|
80355,27205
|
2008
|
65326,96295
|
0,595626729
|
106734,9724
|
2009
|
48181,79158
|
0,601584226
|
123136,7255
|
2010
|
40066,62802
|
0,618493507
|
140595,3803
|
2011
|
55995,47284
|
0,62871467
|
154179,0572
|
2012
|
61579,41172
|
0,640576744
|
172062,6364
|
2013
|
72335,33644
|
0,642367229
|
180439,6332
|
2014
|
74527,73392
|
0,647140703
|
187400,3946
|
2015
|
95594,24183
|
0,656489833
|
202890,7039
|
2016
|
114999,5849
|
0,668367605
|
225998,4424
|
2017
|
125157,5705
|
0,678830227
|
247948,193
|
2018
|
139831,308
|
0,689145455
|
164111,1033
|
Рис.3.1. Прогноз на 2018 год
Общий экспорт региона к 2018 году должен добраться до высокой отметки. Экспорт региона отражает развитие экономики региона в целом. Повышение данного фактора обусловленно богатой ресурсной базой и развитию лидирующих отраслей региона.
Рис.3.2. Прогноз на 2018 год
Экспорт лесной продукции медленно, но верно продолжает двигаться вверх. Лесопромышленный комплекс региона является лидером по количеству ресурсов и экспорту. Исчезновение лесов ставит под вопрос дальнейшее развитие экспорта, но на близкую перспективу прогнозируется дальнейший рост экспорта и лидирующее место.
Рис.3.3. Прогноз на 2018 год
Наличие больших запасов минеральных продуктов позволяет данному показателю расти с огромной скоростью. Освоенные месторождения позволяют увеличивать экспорт данного ресурса. Большое количество неразвитых месторождений позволяет сказать что с определенным количеством инвестиций данный показатель может занять лидирующее место в регионе и конкурентно-способную позицию на рынках.
Вывод на основе проведенного анализа. Из модели и графиков следует вывод,что инфраструктура оказывает важное влияние на развитие экспорта региона. Развитая инфраструктура влечет за собой экономическое развитие региона. Экспорт для Архангельской области является одним из важным показателей, так как являясь важной части для России, Архангельская область является лидером в сфере ЛПК и добычи минеральных полезных ископаемых
|
 Скачать 1.08 Mb.
Скачать 1.08 Mb.
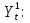
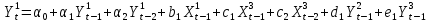
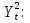
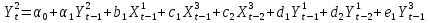
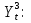
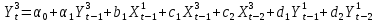
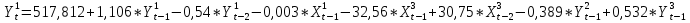
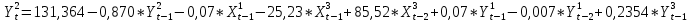
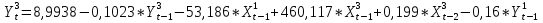
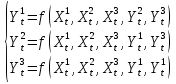 (8)
(8)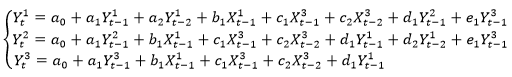 (9)
(9)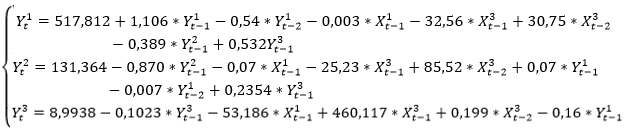
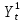 :
: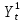 :
: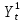 :
: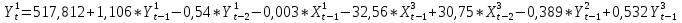
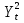 :
: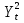 :
: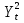 :
: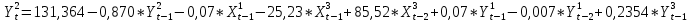
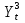 :
: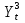 :
: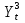 :
: