Гидравлика вариант 5 задач. Задачи гидравлика. Hрт 0,2 м, высота h 1,5 м. Каково при этом показание пружинного вакуумметра Плотность ртути
 Скачать 280.28 Kb. Скачать 280.28 Kb.
|
|
Задача 1.2 Определить абсолютное давление воздуха в баке р1, если при атмосферном давлении, соответствующем ha = 760 мм рт. ст., показание ртутного вакуумметра hрт = 0,2 м, высота h = 1,5 м. Каково при этом показание пружинного вакуумметра? Плотность ртути ρ = 13600 кг/м3. 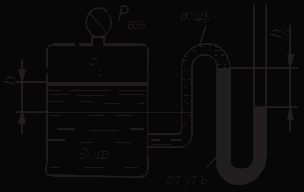 К задаче 1.2 Решение Для решения этой задачи используем основное уравнение гидростатики, позволяющее определить давление в любой точке жидкости и понятие «поверхность равного давления». Как известно, для неподвижной ньютоновской жидкости поверхности равного давления представляют совокупность горизонтальных плоскостей. В данном случае в качестве поверхностей равного давления возьмем две горизонтальные плоскости - поверхность раздела воды и воздуха в соединительной трубке и поверхность раздела воздуха и ртути в правом колене ртутного вакуумметра. Для первой поверхности давление в точках А и В одинаково и согласно основного уравнения гидростатики определяется следующим образом: pА = pВ = p1 + ρ · g · h , (1) где р1 - абсолютное давление воздуха в баке. Из этого уравнения следует , что: p1 = pA - ρ · g · h. (2) Если не учитывать плотность воздуха, то можно записать что pА = pВ = pЕ, т.е. давления в точках А,В, и Е одинаковы. Для второй поверхности давления в точках С и Д одинаковы и равны атмосферному, ра = рС = рД. (3) С другой стороны, давление в т. С можно представить как 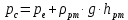  (4) (4)Откуда pе = pа – ρрт·g · hрт. (5) Подставив выражения для рА в уравнение для определения р1, получим р1 = pa - ρрт · g · hрт – ρ · g · h = ρрт · g · (ha - hрт) – ρ · g · h. (6) Численную величину р1 найдем, подставив численные значения величин в правой части уравнения: р1 = 13600 · 9,81 · (0,76 – 0,2) – 1000 · 9,81 · 1,5= = 74713 – 14715 = 59998Па = 60кПа. Разрежение, которое будет показывать вакуумметр: рвак = ра – р1 = ρрт · g · hа – р1= (7) =13600 · 9,81 · 0,76 · 10-3- 60 = 101,4 – 60 = 41,4кПа. Ответ: рвак = 41,4кПа. Задача 2.4 Для опорожнения резервуара с нефтью в дне его имеется плоский круглый клапан диаметром d=100 мм. Определить какую силу Т нужно приложить к тросу для открытия клапана при глубине нефти в резервуаре H=4,2 м. Манометрическое давление паров нефти в резервуаре 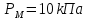 . Как изменится усилие Т, если перед открытием клапана изменить давление на поверхности нефти до нормального атмосферного. . Как изменится усилие Т, если перед открытием клапана изменить давление на поверхности нефти до нормального атмосферного.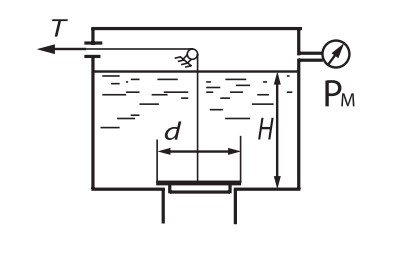 Решение Площадь клапана 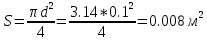 , ,Давление на клапан 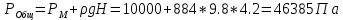 Так как сила 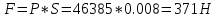 , ,то усилие Т должно быть больше, чем сила F, равная 371 Н. Если изменить давление на поверхности нефти до нормального атмосферного, то давление 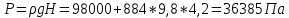 , ,а сила 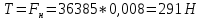 . .Т.е. в случае, когда на поверхности нефти действует нормальное атмосферное давление сила Т уменьшится на 80 Н. Задача 3.6 Бензин сливается из цистерны по трубе диаметром d = 50 мм, на которой установлен кран с коэффициентом сопротивления ζкр = 3. Определить расход бензина при Н1 = 1,5 м и Н2 = 1,3 м, если в верхней части цистерны имеет место вакуум hвак = 73,5 мм рт. ст. Потерями на трение в трубе пренебречь. Плотность бензина ρ = 750 кг/м.   1 1 1 1       2 2  2 2 Решение Запишем уравнение Бернулли для сечений 1 – 1 и 2 – 2 относительно плоскости сравнения, совпадающей с сечением 2 – 2. 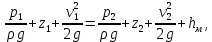 (1) (1)где 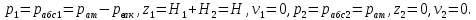 Тогда уравнение (1) примет вид 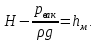 Потери напора в местных сопротивлениях определим по формуле 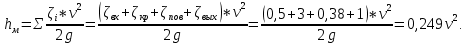 Тогда 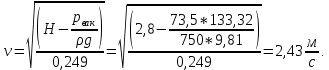 Тогда расход бензина составит 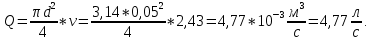 Ответ: Q = 4,77 л/с Задача 4.8 Определить значение силы F, преодолеваемой штоком гидроцилиндра при движении его против нагрузки со скоростью υ =20 мм/с. Давление на входе в дроссель рн = 20 МПа; давление на сливе рс = 0,3 МПа; коэффициент расхода дросселя μ = 0,62; диаметр отверстия дросселя d = l,2 мм; D = 70 мм; dш = 30 мм; ρ = 900 кг/м³. 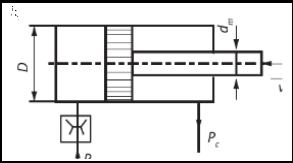 Решение Поскольку поршень движется равномерно со средней скоростью или Силы, действующие слева: Силы, действующие справа: Тогда равновесие сил будет выражаться уравнением: или где Сила, действующая на поршень, определяется по формуле: Рабочее давление гидроцилиндра: где тут Расход гидроцилиндра определяем из условия равенства расходу, проходящему через дроссель: откуда  (15) (15)Тогда  (16) (16)где подставляем полученные результаты в выражение (16)  По формуле (12) находим давление в левой полости цилиндра: Подставляя полученные значения в формулу (11) определяем искомую силу, действующую на поршень  Ответ: F = 55 кН. Задача 5.10 Какой предельной длины L можно сделать пожарный рукав диаметром D=65 мм, если при давлении рм=0,8 МПа (по манометру на гидранте) подача через установленный на конце ствола насадок, выходной диаметр которого d=30 мм, должна составлять Q=1,2 м3/мин? Ствол поднят выше манометра на h=10 м; коэффициент сопротивления ствола с насадком ζ=0,1 (сжатие струи на выходе отсутствует). Местные потери в рукаве не учитывать. Задачу решить, предполагая, что используются непрорезиненные (λ=0,054) и прорезиненные (λ=0,025) рукава.  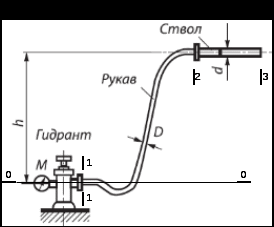 Решение Составляем уравнение Бернулли для сечений 1-1 и 2-2, относительно плоскости сравнения 0-0:  (1) (1)где Тогда уравнение Бернулли принимает вид:  (2) (2)откуда  (3) (3)Суммарные потери напора между сечениями 1-1 и 2-2:  (4) (4)Подставляя выражение (4) в выражение (3), получаем:  (5) (5)откуда находим предельную длину пожарного рукава  (6) (6)Составляем уравнение Бернулли для сечений 2-2 и 3-3, относительно плоскости сравнения 0-0:  (7) (7)где  (8) (8)откуда Потери напора в стволе с насадком:  (10) (10)Скорость воды на выходе из насадка:  тогда  и по формуле (9) Из уравнения неразрывности потока: находим По формуле (6) определяем предельную длину пожарного рукава: - непрорезиненного  - прорезиненного  Ответ: L1=17,3 м, L2=37,4 м. |
