ВЛИЯНИЕ ЗАМИРАНИЙ И РАССИНХРОНИЗАЦИИ СИГНАЛОВ НА ПОМЕХОУСТОЙЧИВО. Httpinfo alnam rubook tinf phpid48 влияние замираний и рассинхронизации сигналов на помехоустойчивость
 Скачать 180.5 Kb.
|
http://info.alnam.ru/book_tinf.php?id=48ВЛИЯНИЕ ЗАМИРАНИЙ И РАССИНХРОНИЗАЦИИ СИГНАЛОВ НА ПОМЕХОУСТОЙЧИВОСТЬРассмотрением влияния замираний и рассинхронизации сигналов на помехоустойчивость передачи сигналов завершается анализ влияния на помехоустойчивость тех основных факторов, которые вызывают существенное отклонение условий приема сигналов от идеальных. Полученные результаты, рассматриваемые совместно с результатами § 6.3-6.5, позволяют достаточно полно определить реальную помехоустойчивость различных систем. 6.6.1. Влияние замираний сигналов на помехоустойчивость. До сих пор рассматривались задачи приема сигналов для каналов с постоянными параметрами и аддитивной помехой. Рассмотрим, как полученные результаты обобщаются для каналов с переменными случайными параметрами, когда имеются замирания сигналов (см. § 4.1). В этом случае принятый сигнал  Обозначим математическое ожиданиеслучайного процесса  через  предположим, что центрированный процесс  является стационарным случайным процессом с нулевым математическим ожиданием и дисперсией  Подставим  в выражение для  тогда Отличием рассматриваемого случая от ранее изученных является то, что сигнал умножается на среднее значениекоэффициента передачи канала а эквивалентная аддитивная помеха  уже не является стационарным случайным лроцессом. Математическое ожидание помехи  а дисперсия зависит от времени, так как Следовательно, помимо усреднения по множеству, необходимо применять усреднение и по времени. Взаимная энергия принятого и передаваемого сигналов 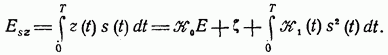 Предположим, что замирания сигнала являются медленными и интервал корреляции процесса намного больше длительности сигнала, тогда 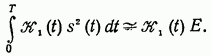 Энергия этого сигнала  С учетом (6.8) отношение сигнал/помеха на входе решающей схемы  Если  является гауссовским белым шумом, то  и где  коэффициент вариации процесса  Из (6.113) следует, что отношение сигнал/шум полностью определяется вариацией коэффициента передачи канала. Для расчетов вероятностей ошибок необходимо учитывать, что из-за замираний сигнала отношение сигнал/шум изменяется пропорционально случайной величине 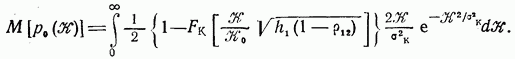 Поэтому вероятности ошибок являются функцией случайного аргумента  Для расчета помехоустойчивости необходимо определять математические ожидания этих функций с учетом одномерного закона распределения коэффициента передачи канала. При релеевских замираниях коэффициент передачи подчиняется распределению (2.78) с учетом соотношений, приведенных в п. 4.1.3, поэтому математическое ожидание вероятности ошибки при оптимальном когерентном приеме двоичных сигналов Интегрирование по частям дает  При  можно применять приближенную формулу При релеевских замираниях (см. п. 4.1.3) и оптимальном некогерентном приеме двоичных сигналов в системах с активной паузой 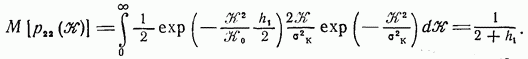 При квазирелеевских замираниях и оптимальном некогерентном приеме   где  Формула (6.117) является наиболее общей для анализа влияния замираний сигналов на помехоустойчивость оптимального некогерентного приема. При  она переходит в (6.116), при  в формулу средней вероятности ошибки при слабых (гауссовых) замираниях, когда коэффициент передачи распределен по нормальному закону с параметрами  Кривая 3 на рис. 6.7 показывает влияние релеевских замираний на среднюю вероятность ошибки (6.115) оптимального когерентного приема двоичных систем с активной паузой. Сравнение кривых  показывает, что замирания сигналов существенно снижают помехоустойчивость. Графики, характеризующие помехоустойчивость оптимального когерентного приема при гауссовых замираниях и обобщенных релеевских, будут находиться в области между кривыми  так как кривая 1 построена для канала без замираний.Кривая 4 показывает влияние релеевских замираний на помехоустойчивость (6.116) оптимального некогерентного приема систем с активной паузой. При гауссовых и квазирелеевских замираниях кривые, характеризующие помехоустойчивость некогерентного приема, будут лежать в области между кривыми 2 и 4, так как кривая 2 построена при отсутствии замираний. Сравнение графиков показывает, что замирания сигналов несколько больше влияют на помехоустойчивость оптимального некогерентного приема. Используем исходные данные п. 6.4.3 и рассчитаем помехоустойчивость оптимального некогерентного приемника ЧМ сигналов при релеевских замираниях при условии, что  В соответствии с формулой  Следовательно, релеевские замирания приводят к тому, что помехоустойчивость рассматриваемого приемника ухудшается в 3,38 раза по сравнению со случаем без замираний и в 1,42 раза по сравнению с когерентным приемником при таких же замираниях.Для борьбы с замираниями используют: автоматическую регулировку усиления (АРУ) сигналов и разнесенный прием сигналов применяют широкополосные (шумоподобные) сигналы (см. § 3.3) и другие методы. Действие схемы АРУ сводится к тому, что она обеспечивает коэффициент усиления сигнала  тогда выходной сигналНаличие аддитивной помехи снижает эффективность, так как линейная обработка сигнала производится при флуктуирующей мощности белого шума. Суть разнесенного приема заключается в том, что переданное сообщение в приемнике воспроизводится не по одному принятому сигналу, а по двум или нескольким, несущим одно и то же сообщение. Обработка таких сигналов сводится к тому или иному виду суммирования с весом. В частности, это может быть определение среднего значения сигналов, выбор наибольшего из них и т. п. Различают методы разнесения по частоте, когда один и тот же сигнал одновременно излучается различными передатчиками на различных частотах, по времени — повторение передачи, пространственного разнесения, когда сигналы от одного и того же передатчика принимают на антенны, разнесенные в пространстве или с различной поляризацией. 6.6.2. Влияние рассинхронизации сигналов на помехоустойчивость. Помимо помех, большое влияние на помехоустойчивость оказывает нестабильность параметров приемника, например неточная работа схемы синхронизации, которая проявляется в «рассинхронизации» передаваемых и опорных сигналов. Из-за рассинхронизации вероятности ошибок когерентного и некогерентного приемов возрастают. Рассмотрим особенности оценки этих вероятностей при неидеальной временной синхронизации амплитудно-манипулированных сигналов. Для других видов модуляции эти вероятности определяют аналогично [14]. Задача ставится следующим образом: спектральная плотность  белого шума  форма и параметры сигнала  известны точно, требуется определить, как влияет несовпадение момента  прихода сигнала и момента 4 генерирования опорного сигнала на вероятность ощибки приемника. Иначе говоря, необходимо определить влияние закона распределения  на вероятность ошибки. В некогерентном приемнике  характеризует погрешность времени взятия отсчета огибающей на выходе детектора (на входе решающей схемы).При временном рассогласовании 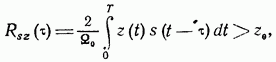 огибающей принимаемого и опорного сигналов условие принятия решения о приходе сигнала имеет вид где  порог сравнения в решающей схеме; нормировка с помощью множителя  выполнена для приведения  к безразмерному виду.Для определения вероятности ошибки как вероятности невыполнения условия (6.118) необходимо по известному распределению 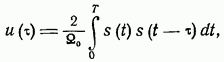 найти распределение  где а затем распределение  суммы По распределению 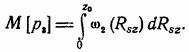 определяют математическое ожидание вероятности ошибки Если рассинхронизация обусловлена погрешностью работы схемы автоподстройки частоты приемника, то распределение  при больших отношениях сигнал/помеха на входе приемника можно полагать нормальным с нулевым средним и дисперсией  Для прямоугольного видеоимпульса длительностью  и энергией  функция  имеет вид равнобедренного треугольника с основанием  и высотой  Следовательно,  Для удобства расчетов введем безразмерное среднеквадратическое значение времени расстройки  После выполнения необходимых промежуточных преобразований получим где С — нормировочный множитель усеченного гауссовского  пределения  Распределение 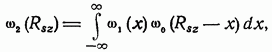 определим как свертку [15] распределений   что справедливо при условии независимости помех в цепи синхронизации и на входе приемника. Вычислив интеграл (6.123) с учетом того, что  является гауссовским распределением с нулевым средним и дисперсией  получим: где   функция Лапласа (2.90).В соответствии с (6.121) математическое ожидание вероятности ошибки при бинарных равновероятных сигналах 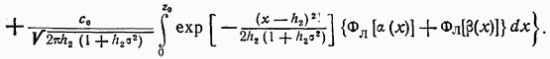  Если синхронизация идеальная, то  и формула (6.125) переходит в известную (6.57) при  определяемом из (6.62).Анализ зависимостей типа (6.125) обычно производится численными методами с помощью ЦВМ. Численное интегрирование позволяет построить номограммы  Эти номограммы дают возможность определить влияние рассинхронизации на помехоустойчивость. На рис. 6.11 показана одна из таких номограмм. Графики зависимости вероятности ошибки от отношения сигнал/шум построены в логарифмическом масштабе при значении 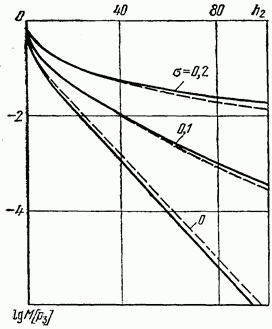 (идеальная синхронизация),  и 0,2. Рис. 6.11. Влияние рассинхронизации на помехоустойчивость приема АМн сигналов 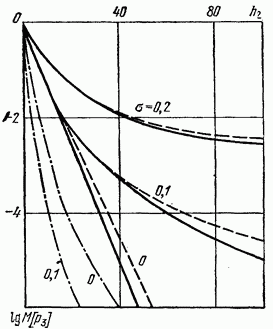 Рис. 6.12. Влияние рассинхронизации на помехоустойчивость приема ЧМ и ФМ сигналов Помехоустойчивость приемника АМн сигналов существенно зависит от точности синхронизации. Например, при  увеличение рассинхронизации на 20% проводит к увеличению вероятности ошибки более чем на два порядка. Влияние рассинхронизации и замираний сигналов на помехоустойчивость примерно одинаково. Для сравнения на рис. 6.11 показаны аналогичные кривые (штриховые линии) для оптимального некогерентного приема. Рассинхронизация примерно одинаково влияет на помехоустойчивость когерентного и некогерентного приемов.На рис. 6.12 показано влияние рассинхронизации на помехоустойчивость приема ЧМ и ФМ сигналов. Кривые построены для когерентного приема ЧМ сигналов при  штриховые кривые отражают аналогичные зависимости для некогерентного приема. Штрих-пунктирные кривые показывают зависимости вероятностейошибок для когерентного приема ФМ сигналов при  Сравнение графиков рис. 6.11», 6.12 позволяет сделать следующие выводы. Рассинхронизация больше всего влияет на помехоустойчивость приема АМн сигналов. Влияние рассинхронизации на помехоустойчивость когерентного и некогерентного приемов примерно одинаковое, существенное различие проявляется лишь в области больших отношений сигнал/шум на входе решающего устройства.Контрольные вопросы |