Httpssoftdroids comindex phpdodownload&id488
 Скачать 5.05 Mb. Скачать 5.05 Mb.
|
еслиx 5. Замечание.Вычислите пределы, стремящиеся справа и слева к x=5, и сравните их. Также вычислите значение функции при x=5. Если все эти зна- чения равны, то функци2я непрерывна в этой точке. 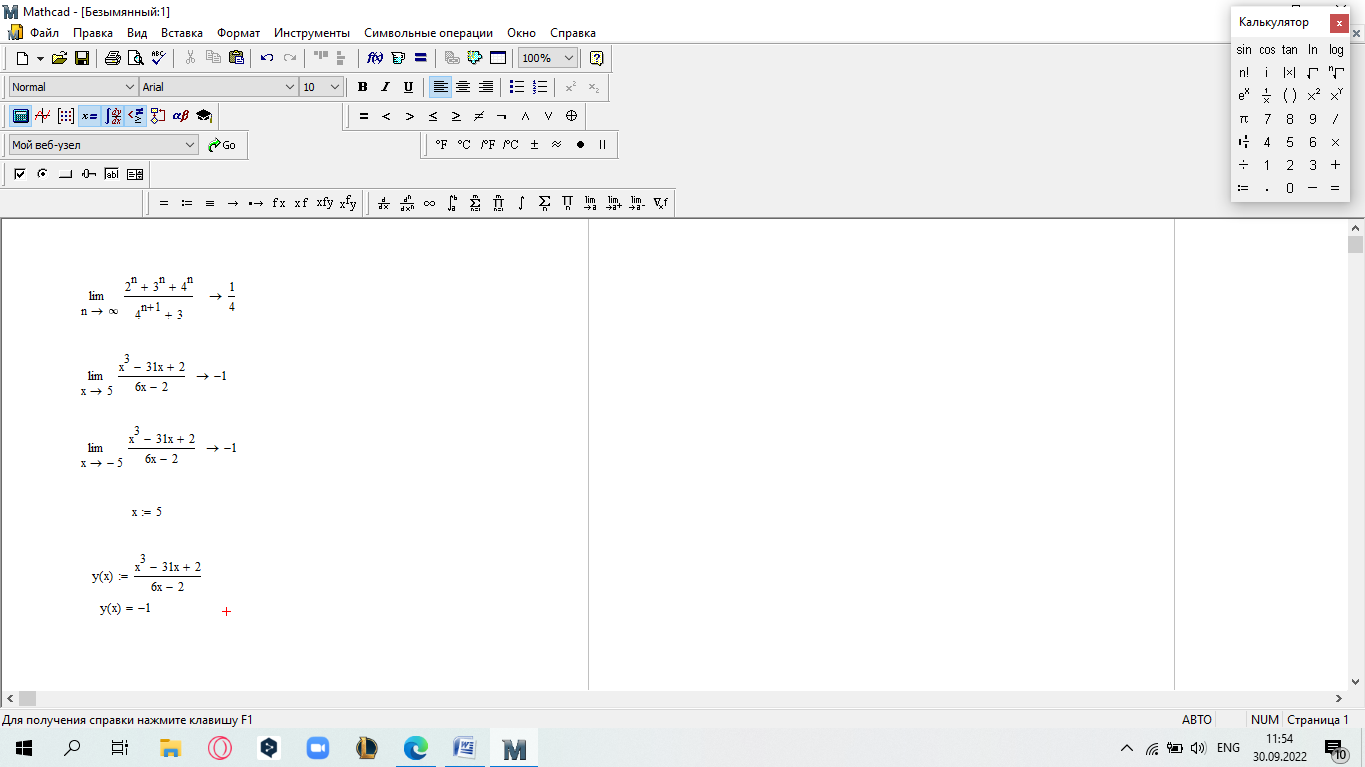 САМОСТОЯТЕЛЬНАЯ РАБОТА 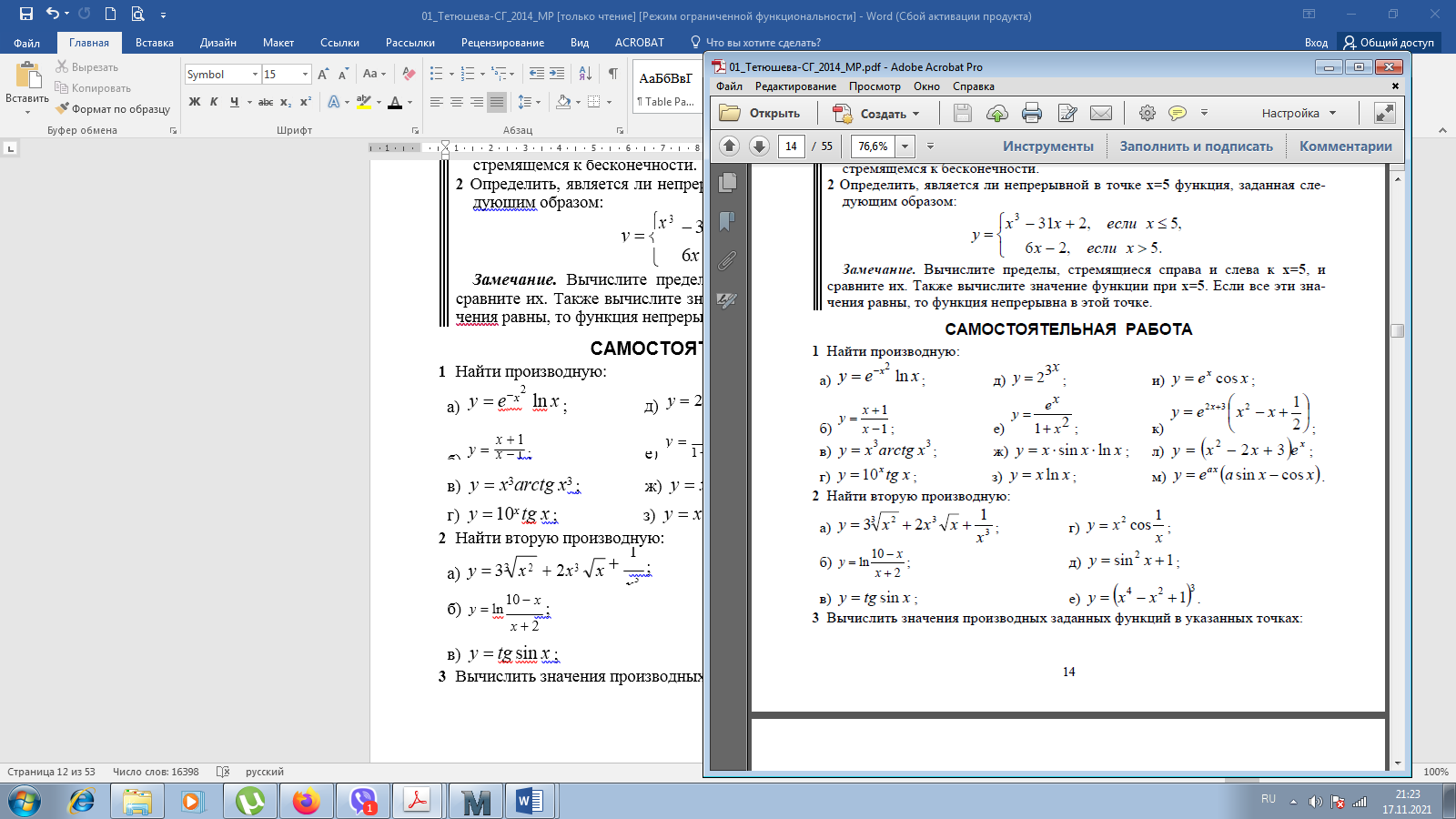 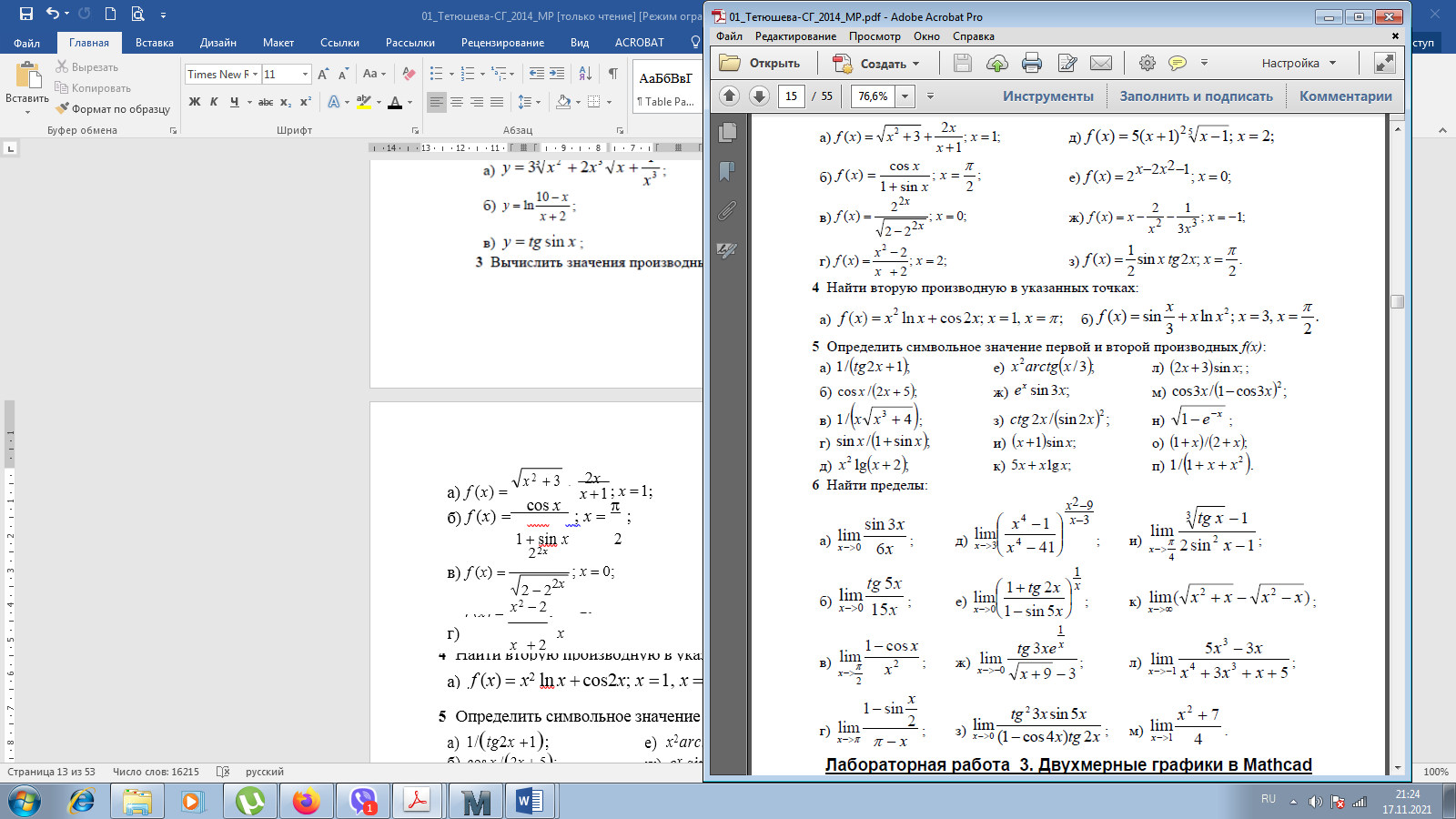 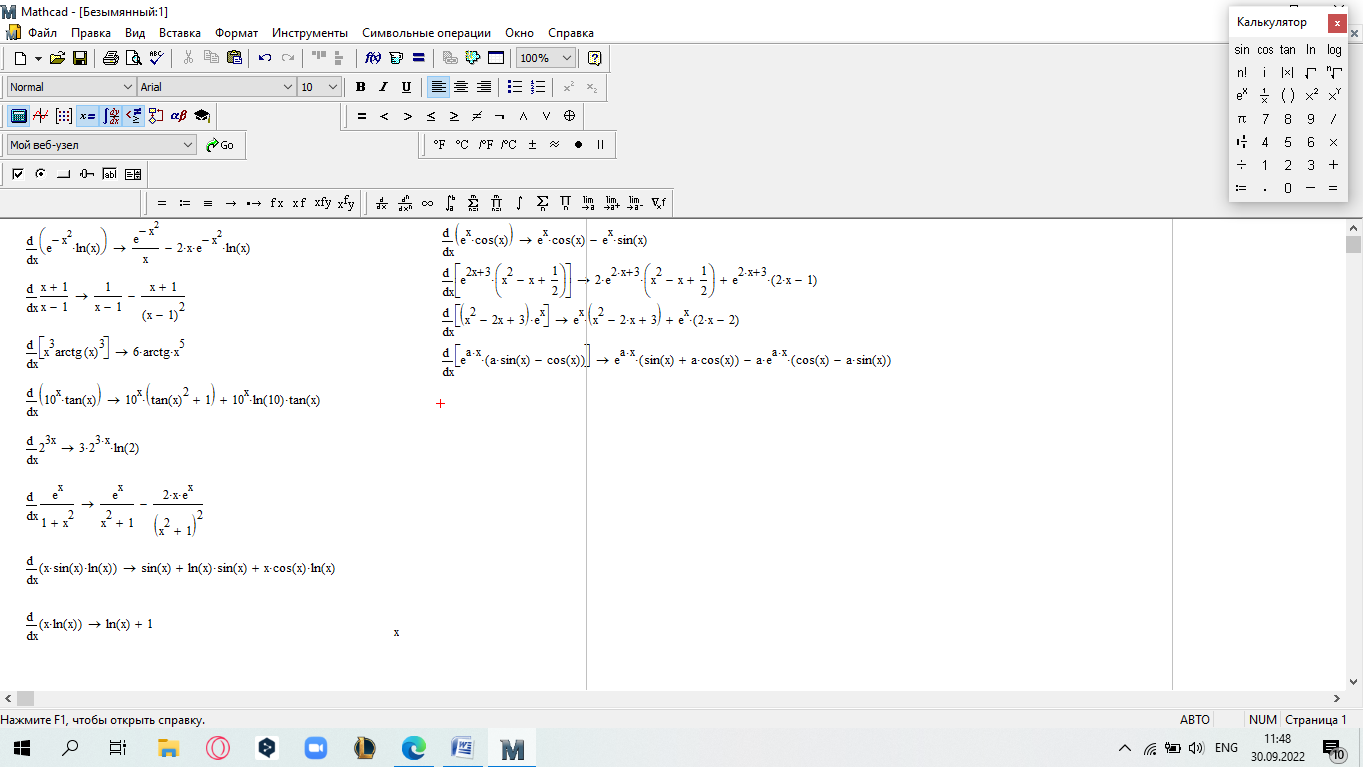 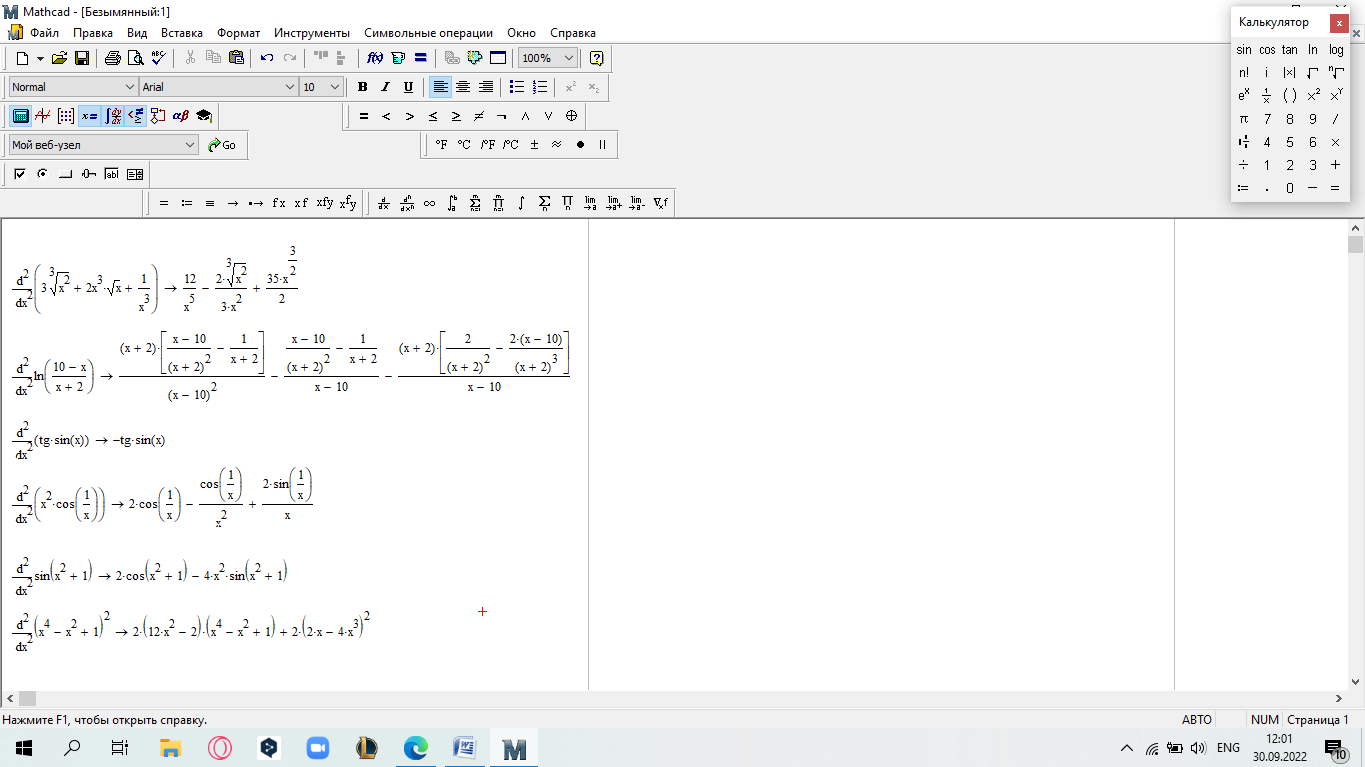 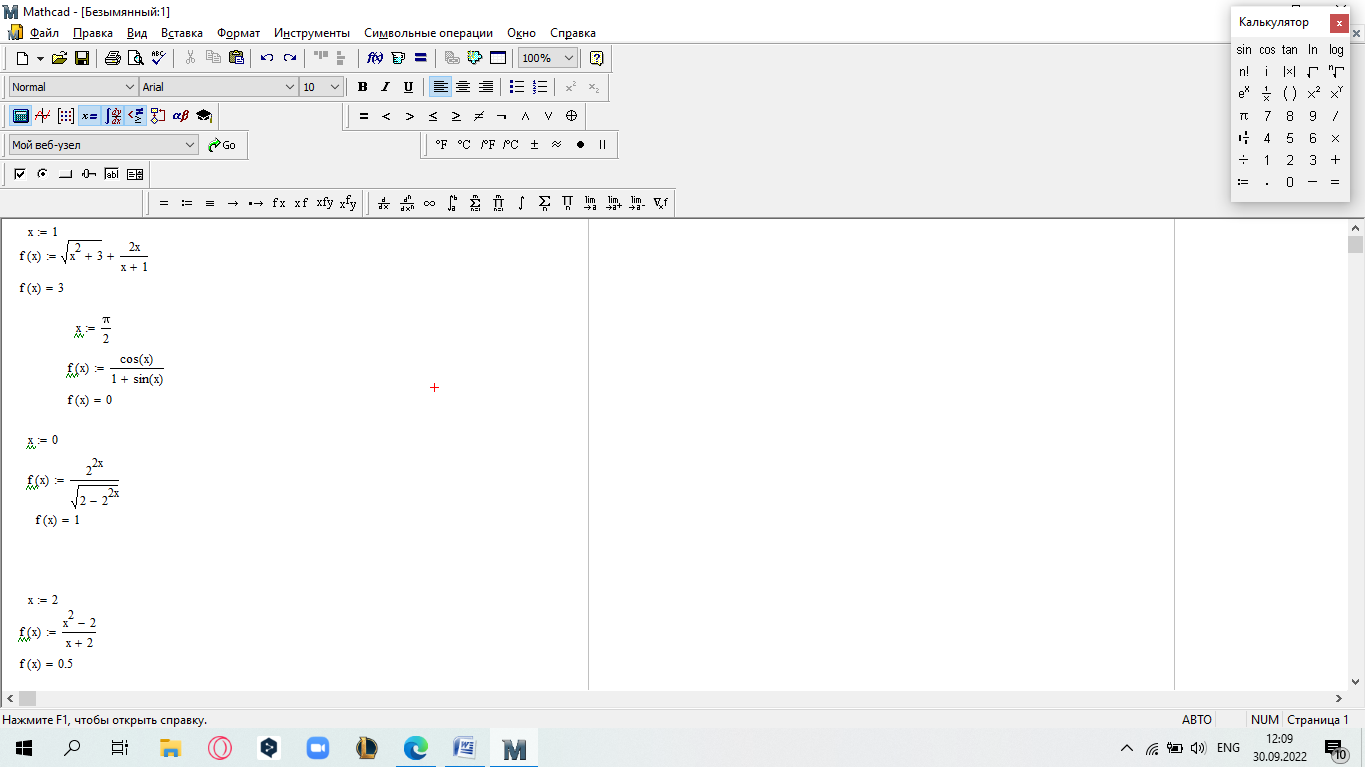 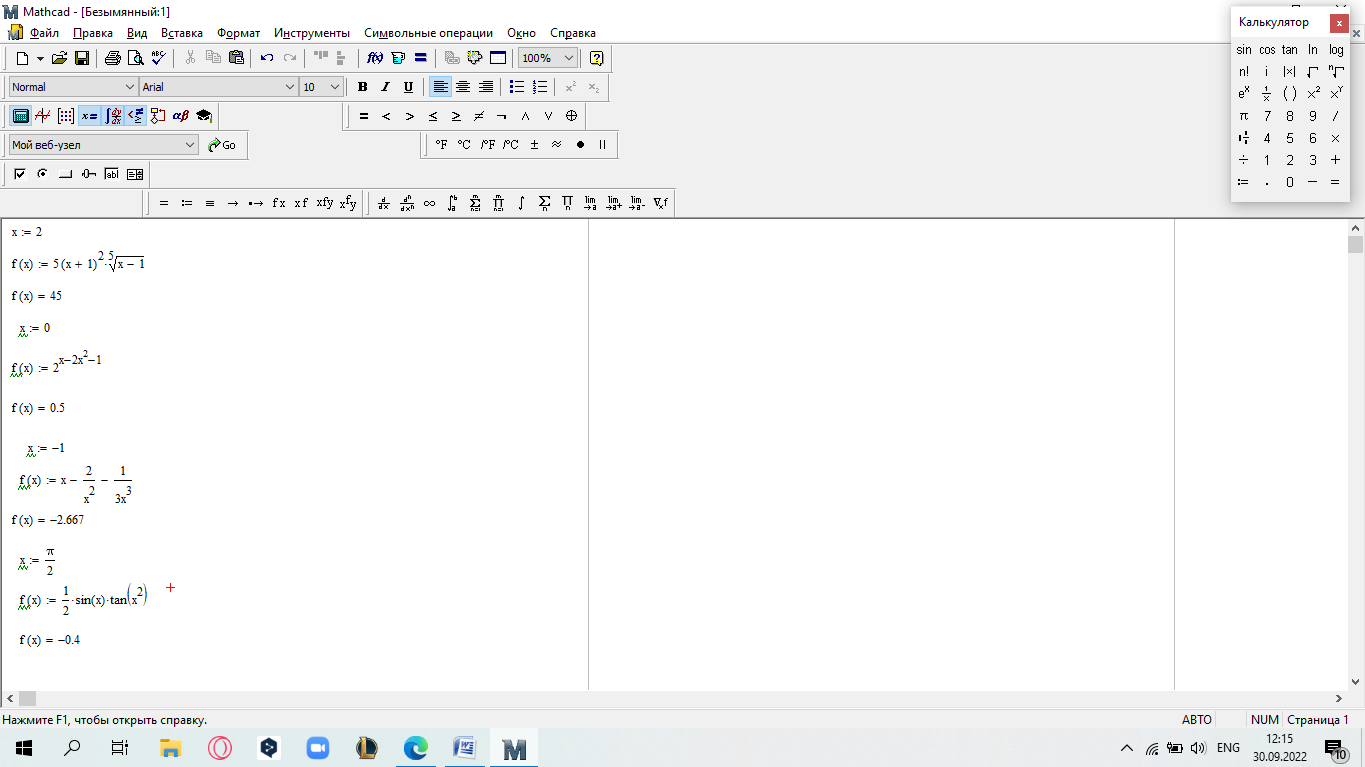 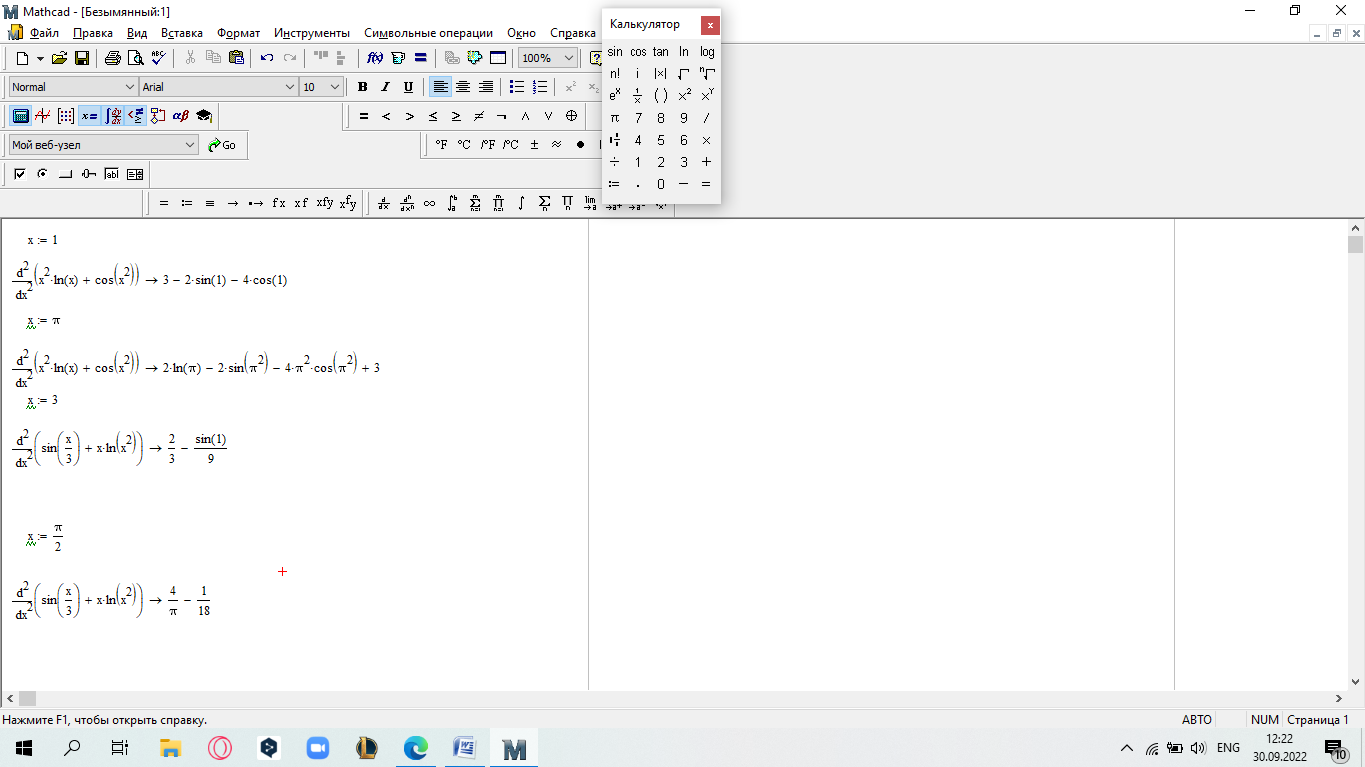 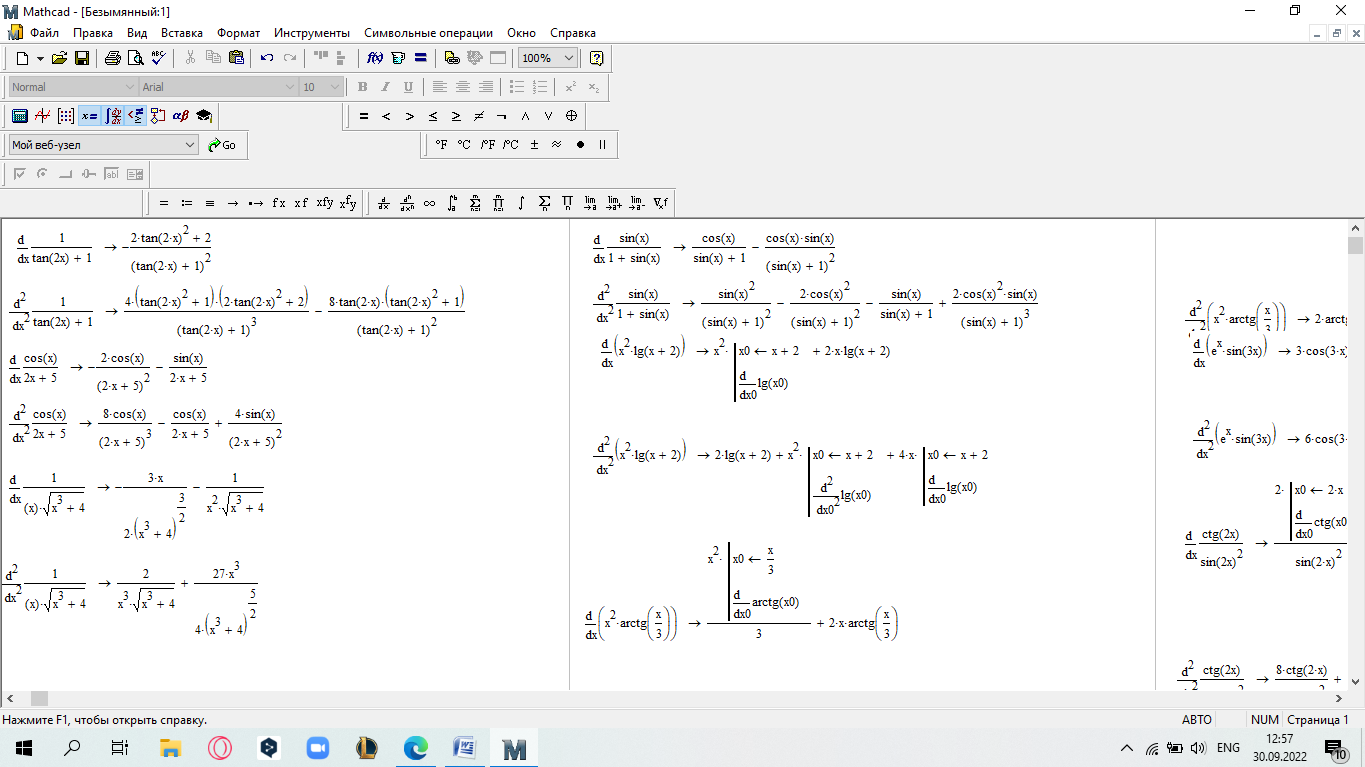 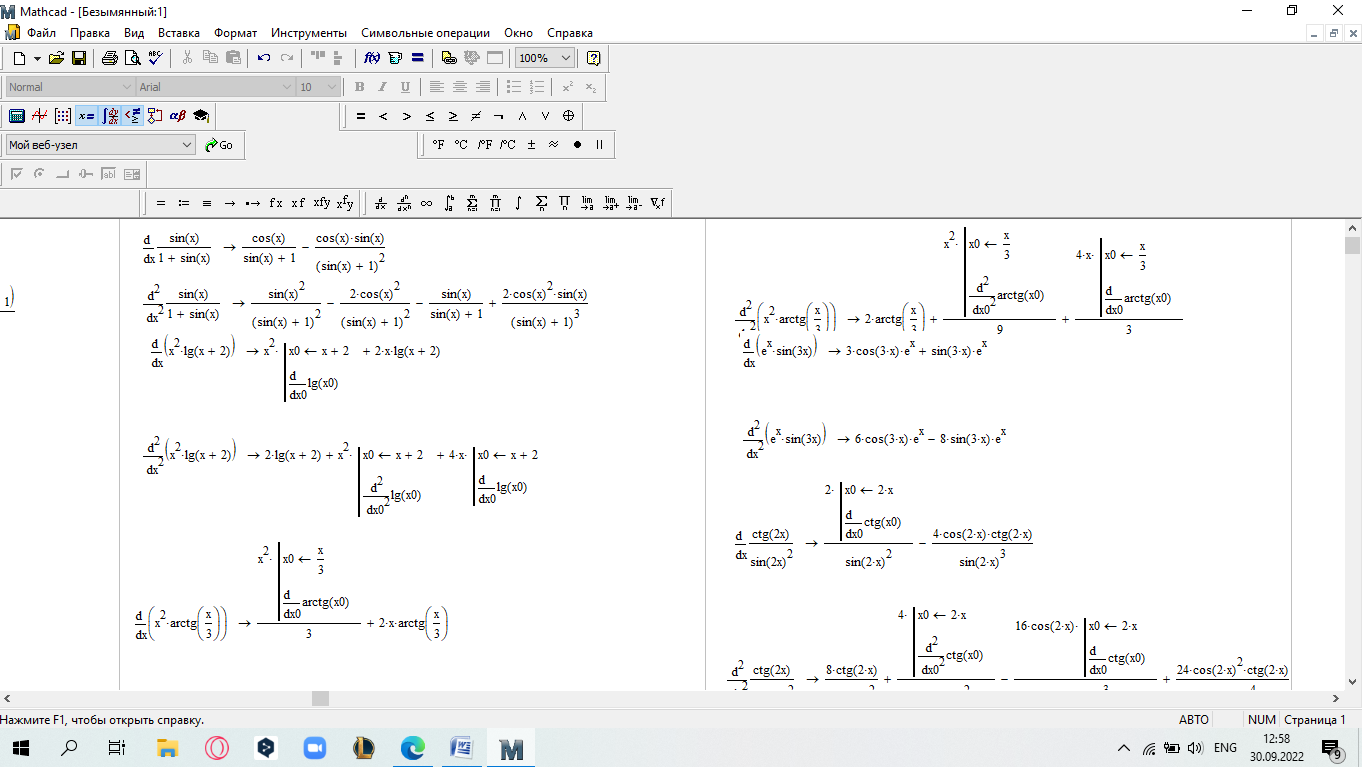 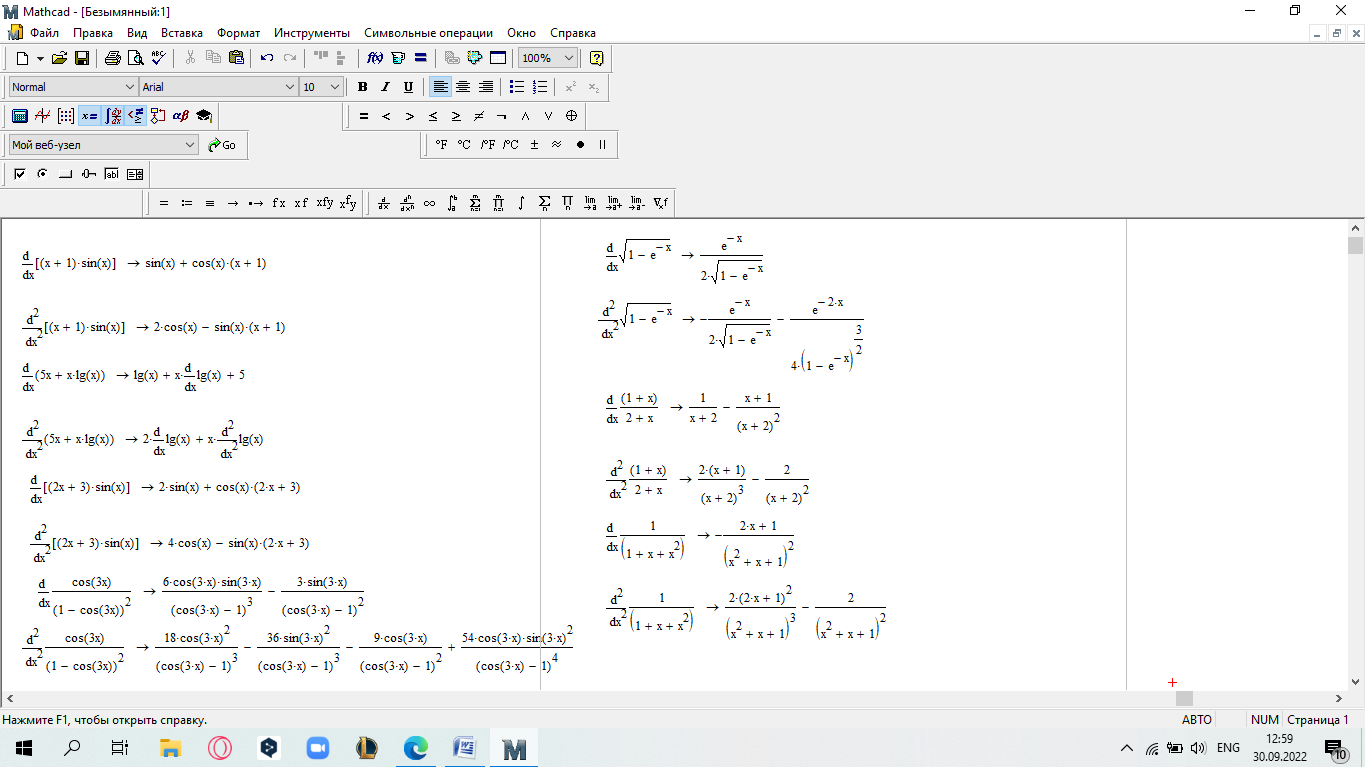 Л 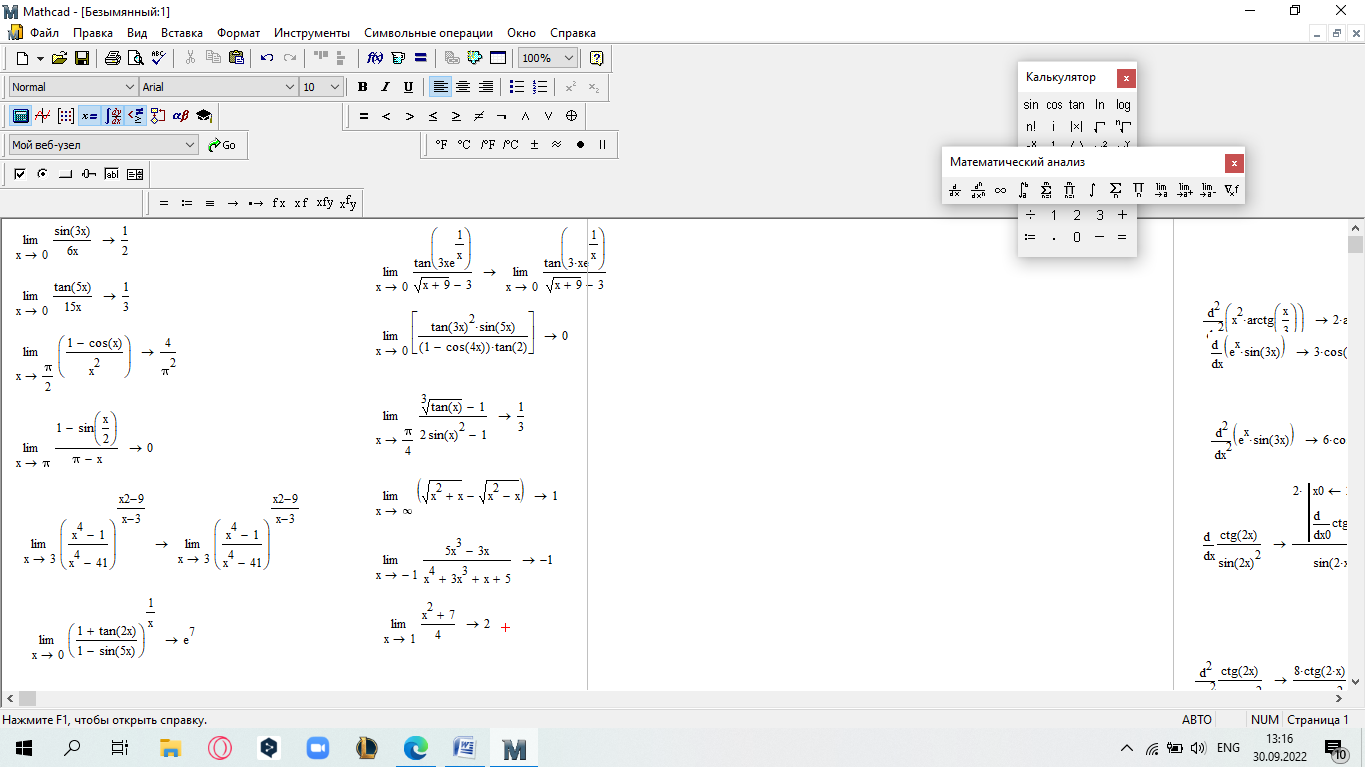 абораторнаяработа3.ДвухмерныеграфикивMathcad абораторнаяработа3.ДвухмерныеграфикивMathcadГрафики в декартовой системе координат Дляпостроенияграфикавдекартовойсистемекоординатнеобходимо: Определить дискретную переменную, которая принимает значения в желае- мом диапазоне значений аргумента, например, x := -10..10. Ввести выражение, описывающее некоторую функцию, например f(x):=x+sin(x). В меню Вставка (Insert) выбрать пункт График (Graph), затем выбрать X-Yкоординаты (X-Y Plot). В документе появится область для построения гра- фика. В поле по оси абсцисс ввести имя дискретной переменной, например х. В среднее поле оси ординат ввести имя функции, например f(x) (рисунок 8). Если функций несколько, то все они записываются в этом поле через запя-тую. Вместо имени функции можно ввести выражение для ее вычисления. 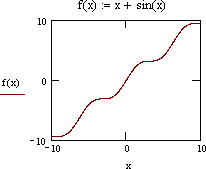 Щелкнуть мимо графического региона или нажать <F9>. Щелкнуть мимо графического региона или нажать <F9>.Рисунок 8 – График функции f(x)=x+sin(x), построенный автоматически  ЗАДАНИЕ 1. Постройте график функции f(x):=x+sin(x) как описано выше. Вы- делите построенный график (рисунок 8). На выделенном графике справа и слева от буквы x стоят числа –10 и 10, которые означают, что график построен на интервале [-10,10]. Изменяя эти значения, можно изменить диапазон по- строения графика. Например, измените число –10 на –1, а число 10 на 1, ука- зывая диапазон построения графика [-1,1]. ЗАДАНИЕ 1. Постройте график функции f(x):=x+sin(x) как описано выше. Вы- делите построенный график (рисунок 8). На выделенном графике справа и слева от буквы x стоят числа –10 и 10, которые означают, что график построен на интервале [-10,10]. Изменяя эти значения, можно изменить диапазон по- строения графика. Например, измените число –10 на –1, а число 10 на 1, ука- зывая диапазон построения графика [-1,1].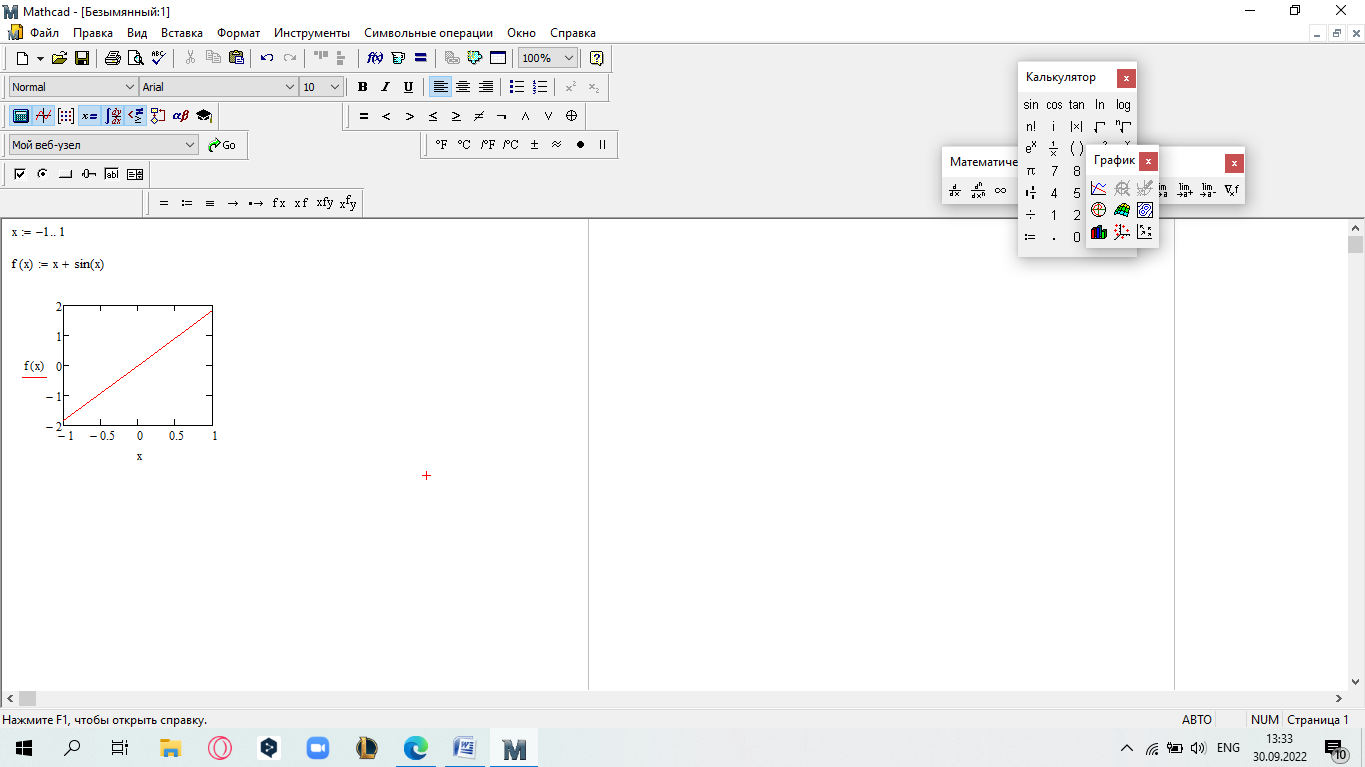  ЗАДАНИЕ2. ЗАДАНИЕ2.1 Построить график функции S=sin(x) для х=0..2 с шагом 0.02. 2 То же для C=cos(x) в новой графической области. Построить график зависимости S(C). Построить в одной системе координат два графика: S=sin(x) и C=cos(x). 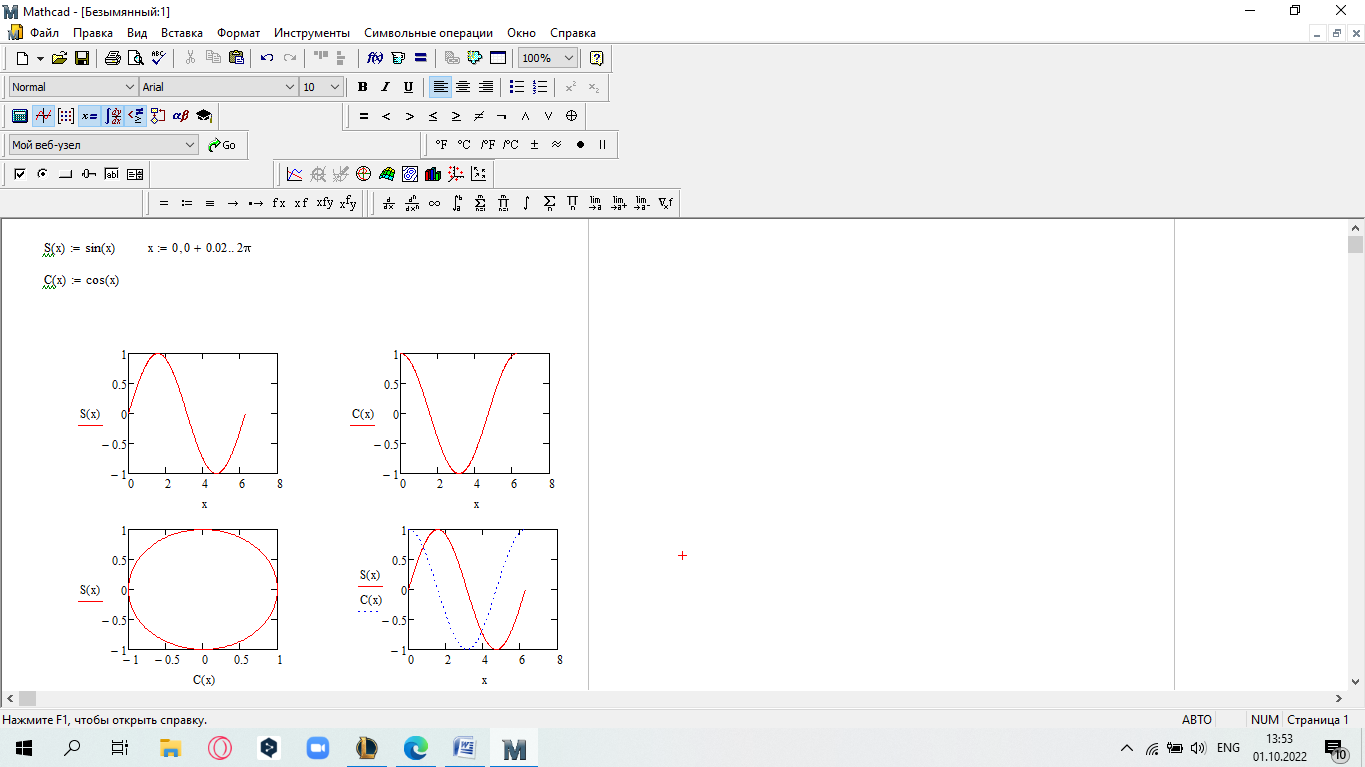 Форматирование двухмерных графиков Для изменения формата уже построенного графика необходимо его выде- лить, затем в меню Формат (Format) выбрать График (Graph). Появившееся диалоговое окно имеет несколько вкладок. На вкладке ОсиХ-Y(X-YAxes) задаются параметры форматирования осей Х и Y (AxisXи AxisY) (рисунок 9): LogScale(мернаялинейка)–установка логарифмического масштаба; GridLines(линиисетки)–установка линий масштабной сетки; Numbered(пронумеровать)–установка цифровых данных по осям; Autoscale(автомасштаб)–автоматическое масштабирование графика; ShowMarkers(показатьмаркеры)– установка рисок по осям; AutoGrid(автосетка)–автоматическая установка масштабных линий; NumberofGrids(числоклетоксетки)– установка заданного числа масштаб- ных линий. 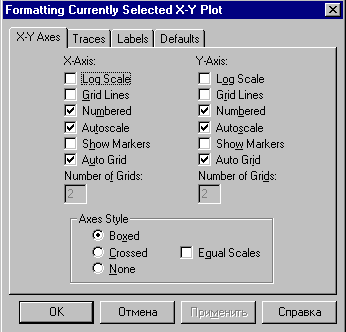 Рисунок 9 –Окно форматирования двухмерных графиков Группа Стиль осей (Axes Style) (рисунок 9) позволяет задать стиль отобра- жения координатных осей: Boxed (рамка) – оси в виде прямоугольника; None(ничего) – отсутствие осей; Crossed (визир) – оси в виде креста; Equal Scales(равныеделения) – одинаковый масштаб по осям. Вкладка Линии графика (Traces) (рисунок 10) служит для управления отоб- ражением линий, из которых строится график: LegendLabel(меткалегенды)–выбор типа линии в легенде; Symbol(символ)–выбор символа для отметки базовых точек графика; Line(линия)–установка типа линий (сплошная, пунктирная и т.д.); Color(цвет)–установка цвета линий и базовых точек; Type(тип)–установка типа графика; Weight(толщина)–установка толщины линий. 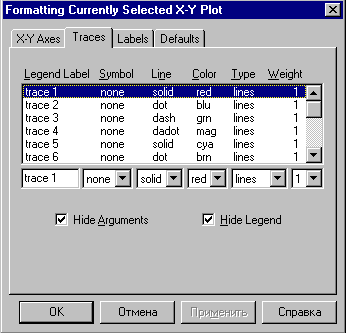 Рисунок 10 –Вкладка Traces Узловые точки графиков (точки, для которых вычисляются координаты) позволяют настроить раскрывающийся в нижней части список столбца Symbol: none (без отметки), box (квадрат), x's (наклонный крестик), dmnd (ромб), +'х(прямой крестик), o's(окружность). Графики отдельных функций можно также выделять, используя для их по- строения линии различного типа, настраиваемые с помощью списка в нижней части столбца Line: solid(непрерывная линия), dot(точечная линия), dash (пунктирная линия), dadot(штрихпунктирная линия). Линии, относящиеся к различным кривым на графике, можно также изме- нить с помощью раскрывающегося списка в нижней части столбца Color. Раскрывающийся список в нижней части столбца Type позволяет выбрать типы линий графика: lines (построение линиями), points (построение точками), error (построение вертикальными черточками с оценкой интервала погрешно- стей), bar (построение в виде столбцов гистограммы), step (построение ступен- чатой линией), draw (построение протяжкой от точки до точки), stem (построе- ние вертикальными черточками). Вкладка Надписи(Label) позволяет вводить в график дополнительные надписи. Для визуализации выбранных параметров при открытом окне их установки служит кнопка Применить каждого диалогового окна. Щелчок на этой кнопке позволяет наблюдать за сделанными изменениями еще до закрытия окна, что заметно облегчает экспериментирование с различными форматами графиков. Пример форматирование двумерного графика приведен на рисунке 11. 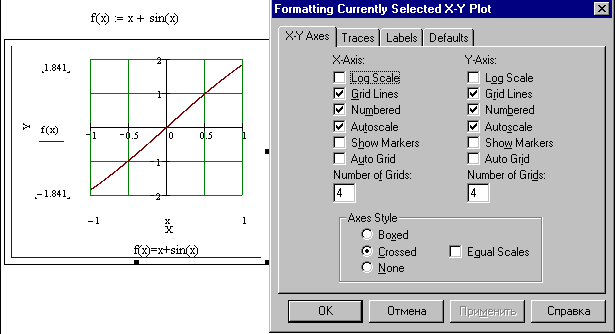 Рисунок 11 –Пример форматирования двухмерного графика Чтобы удалить график, щелкните в его пределах мышью и выберите в меню Edit(Правка) пункт Cut(Вырезать) или Delete(Удалить). Трассировка и масштабирование Трассировка позволяет очень точно изучить строение графика. Для того чтобы включить режим трассировки, щелкните в области графика правой кноп- кой мыши и выберите в контекстном меню пункт Трассировка (Trace) либо выделите график и выполните команду Формат (Format)\ График(Graph)\ Трассировка (Trace). В результате появится окно трассировки (рису- нок 12), а после щелчка в поле графика вы увидите две пересекающиеся пунк- тирные линии. Перемещая указатель мыши по графику, вы тем самым передвигаете точку пересечения линий трассировки. При этом координаты точки указываются с высокой точностью в полях ЗначениеХ(X-Value) и ЗначениеY(Y-Value). 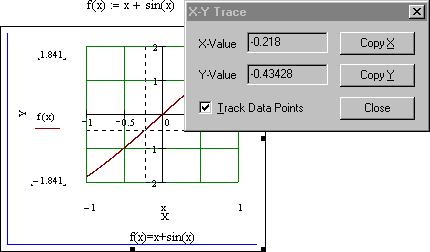 Нажатие кнопки Копировать Х (Copy X) или Копировать Y (Copy Y) копиру- ет соответствующее число в буфер обмена. В дальнейшем его можно вставить в любое место документа. Нажатие кнопки Копировать Х (Copy X) или Копировать Y (Copy Y) копиру- ет соответствующее число в буфер обмена. В дальнейшем его можно вставить в любое место документа.Рисунок 12 –Трассировка графика Если установлен флажок Следовать за рядом данных (Track Data Points) (рисунок12), то линии трассировки следуют точно вдоль линии графика. Еще одно средство для работы с двухмерными графиками заключается в просмотре графика в увеличенном масштабе. Для вызова окна диалога выбери- те в контекстном меню или в меню Формат(Format) пункты График(Graph) и Масштаб (Zoom). После этого указателем мыши выделите прямоугольную область на графике, которую вы хотите просмотреть в увеличенном масштабе (рисунок 13), и нажмите кнопку Увеличить (Zoom). В результате часть графи- ка будет прорисовываться более крупно. 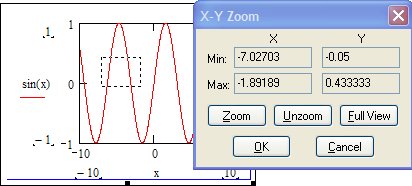 Рисунок 13 –Масштабирование графика Далее можно продолжать изменять масштаб, вернуться к прежнему виду графика кнопкой Показать целиком (Full View) либо закрыть окно диалога для окончательной перерисовки графика в крупном масштабе (нажав кнопку ОК). Графики в полярной системе координат В полярной системе координат каждая точка задается углом fi и модулем радиус-вектора r(fi). График функции обычно строится в виде линии, которую описывает конец радиус-вектора при изменении угла fi в определенных преде- лах, чаще всего от 0 до 2. Чтобы создать график в полярных координатах: 1 Определите приращениедля угла. Например, N:=50. Определите уголкак дискретный аргумент с заданным приращением. Напри- мер, fi:=0,2*/N…2*. Определите радиускак функцию от угла. Например, r(fi):=cos(fi)+1. Щелкните мышью там, где нужно создать график. Выберите в меню Вставка(Insert) пункт Графики(Graph)\ Полярныекоор-динаты(PolarPlot). Появится круг с четырьмя полями ввода. В поле ввода внизу введите угловую переменную графика или любое выра- жение, включающее эту переменную. Например, fi. Поле ввода слева должно содержать выражение для радиуса. Например, r(fi). Два поля ввода справа предназначены для верхнего и нижнего граничных значений радиуса. Mathcad заполняет эти поля автоматически. Нажмите <F9>, чтобы увидеть график. Форматирование графика в полярной системе координат во многом совпа- дает с форматированием графика в декартовой системе координат. Можно построить несколько графиков на одном и том же чертеже в поляр- ных координатах, также как и при построении графиков в декартовых коорди- натах.  ЗАДАНИЕ 3. Построить график зависимости R(fi)=acos(mfi) для fi=-.. с шагом /120 со следующими значениями параметров: a=3, m=2, m=3, m=4. ЗАДАНИЕ 3. Построить график зависимости R(fi)=acos(mfi) для fi=-.. с шагом /120 со следующими значениями параметров: a=3, m=2, m=3, m=4.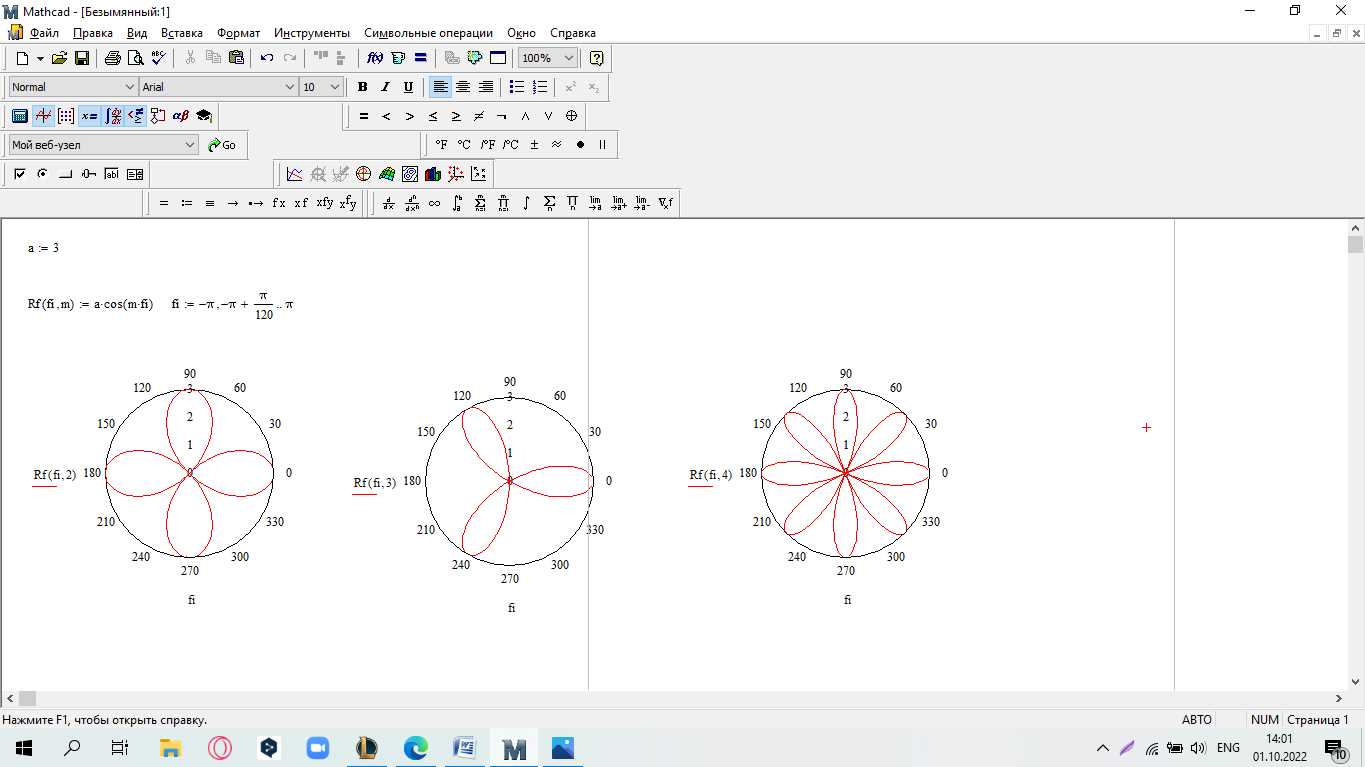  ЗАДАНИЕ4.Постройте кривые, заданные в полярной системе координат (таб- ЗАДАНИЕ4.Постройте кривые, заданные в полярной системе координат (таб-лица 1). Коэффициенты a и b выберите самостоятельно. Для каждой кривой постройте первый график, используя установки формата по умолчанию, а затем постройте второй график, в котором измените установки для осей координат и свойства графика. Таблица 1 –Кривые, заданные в полярных координатах
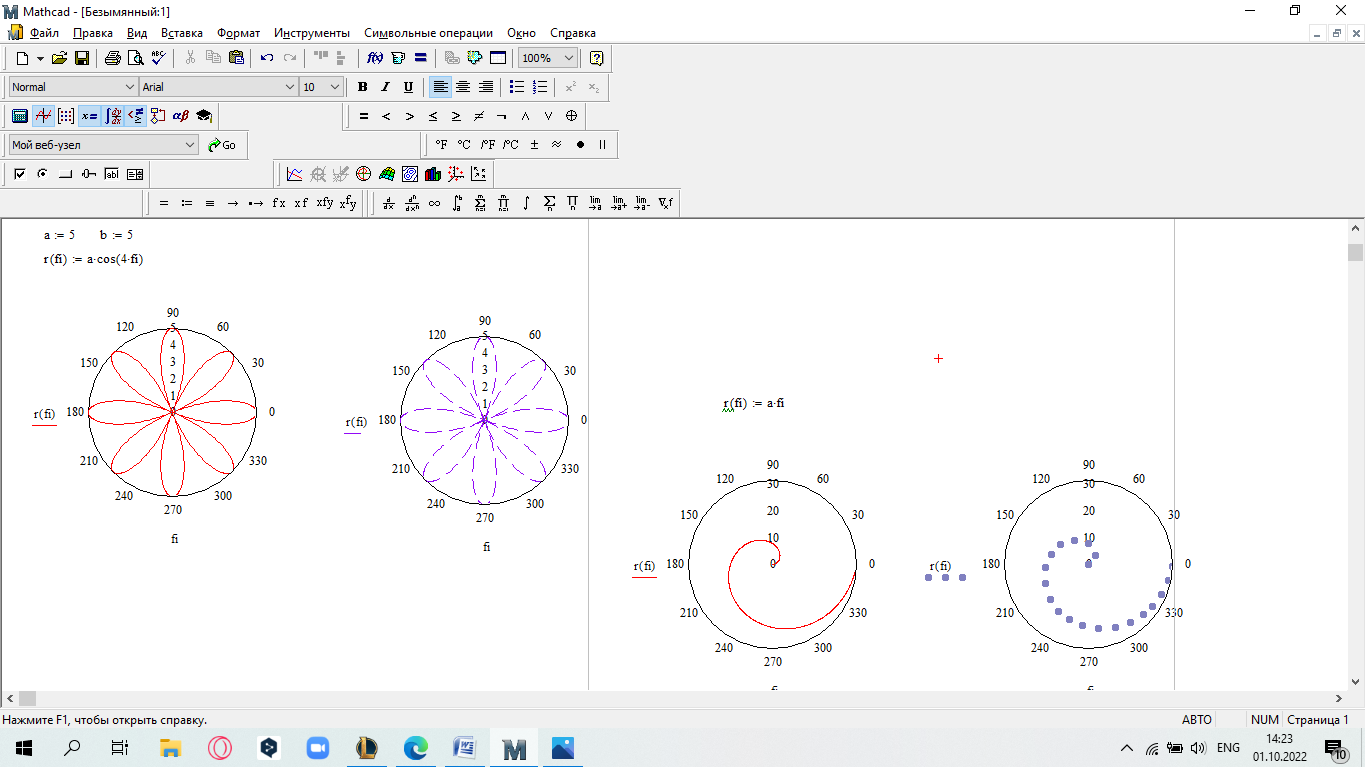 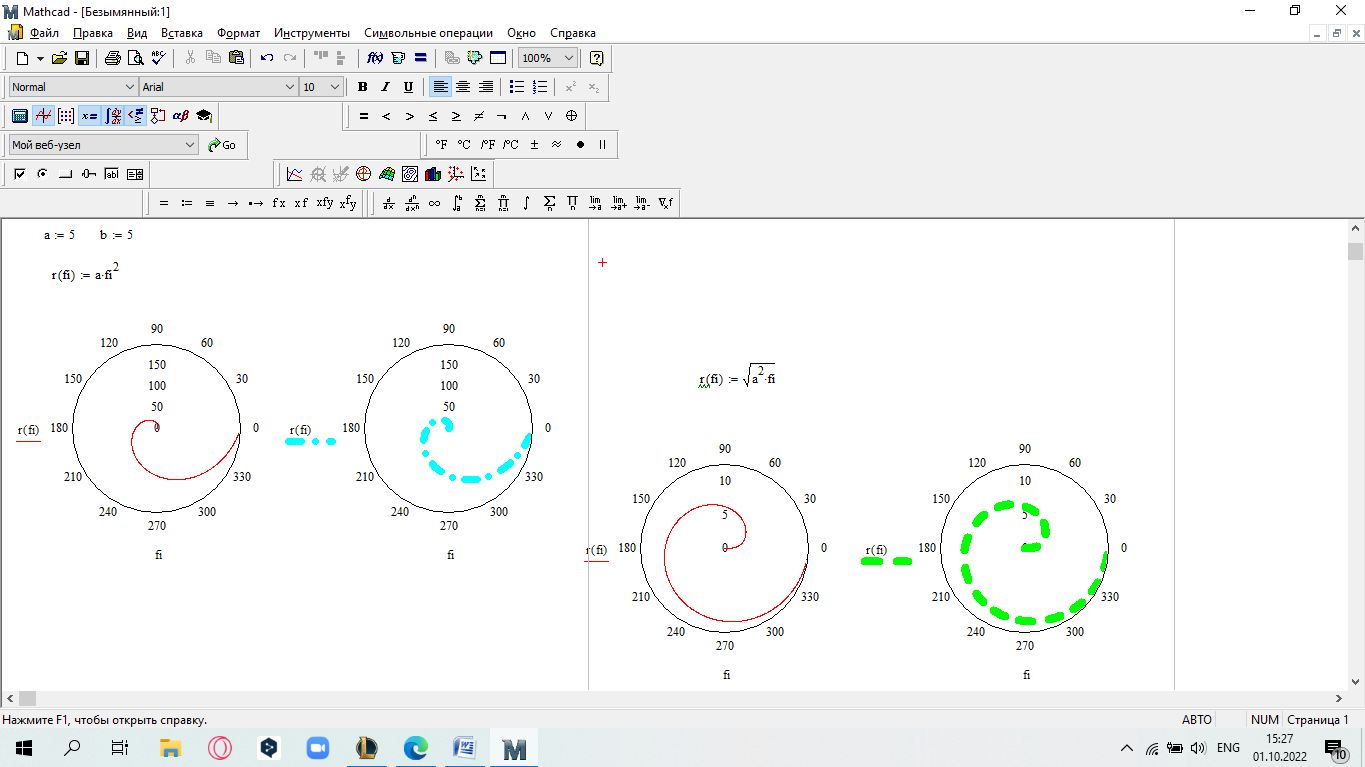 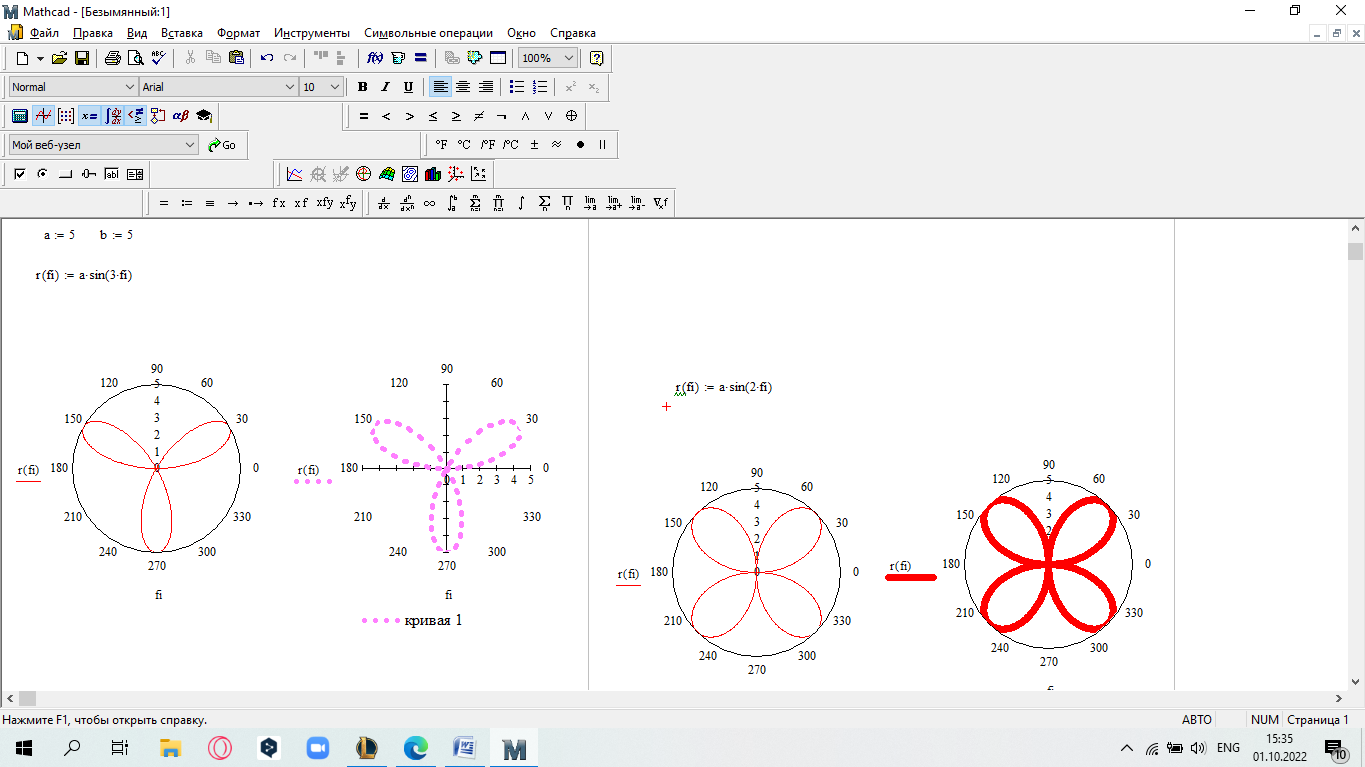 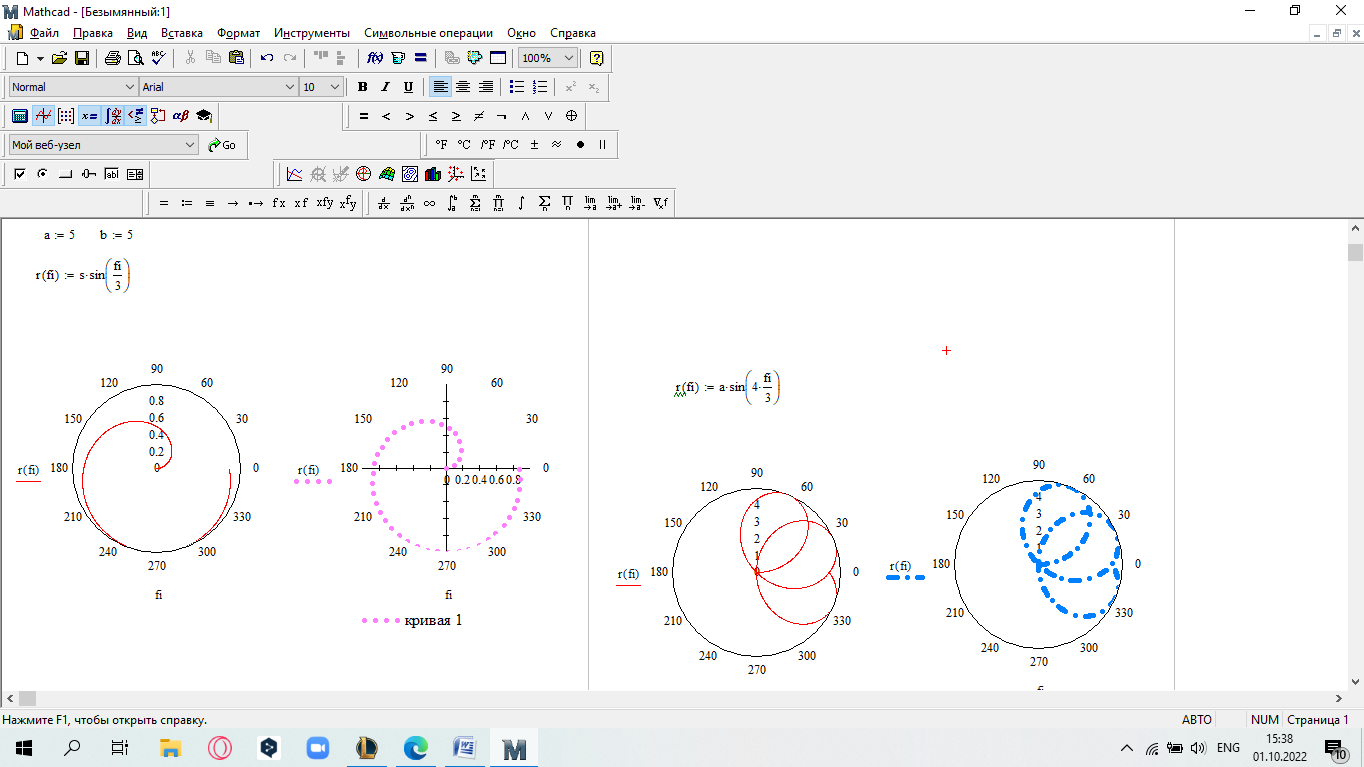 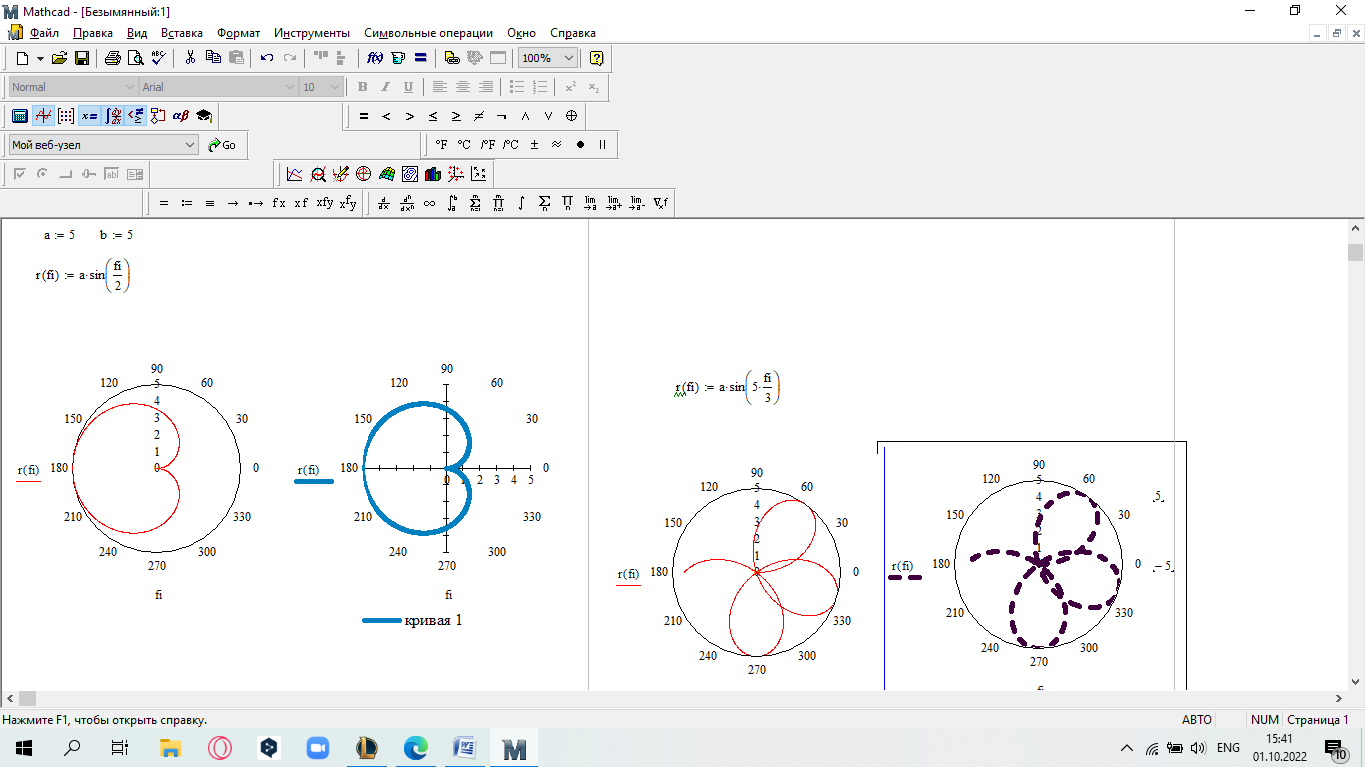 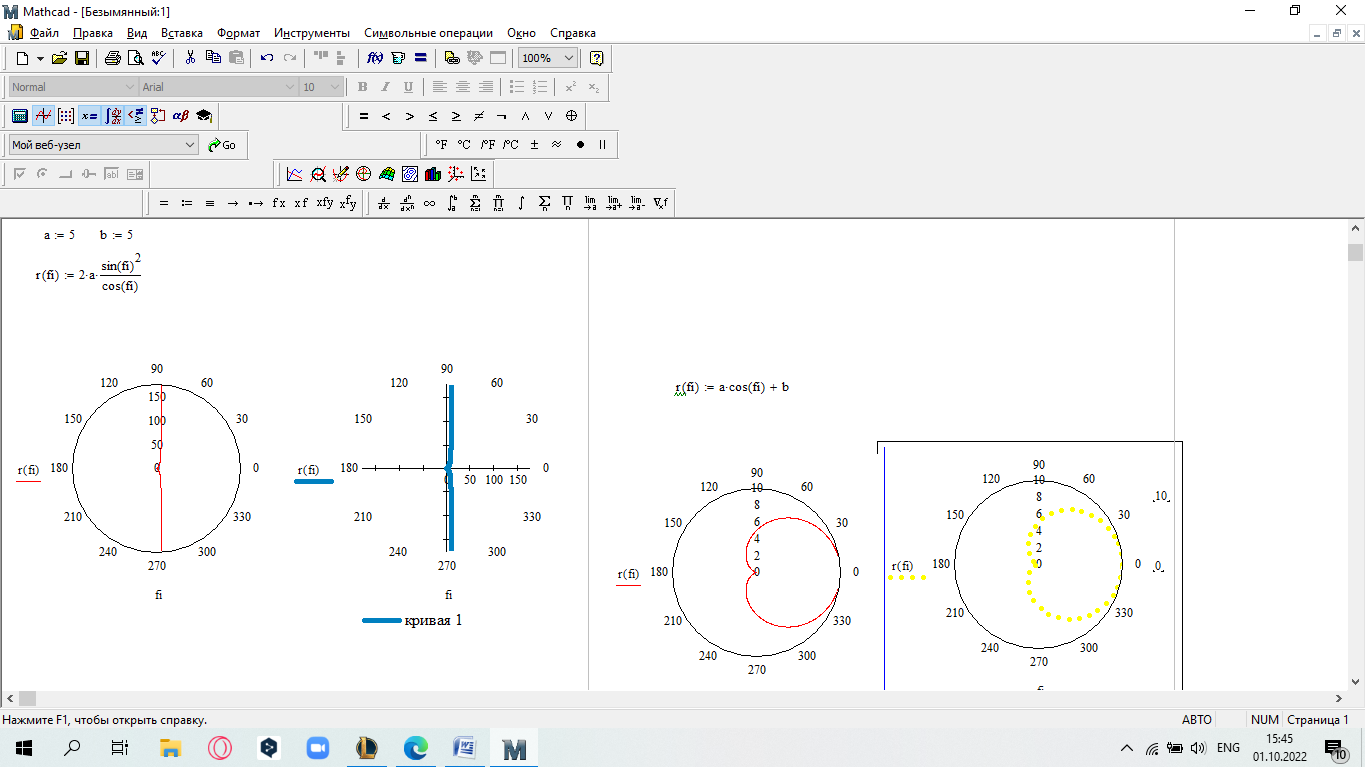 САМОСТОЯТЕЛЬНАЯ РАБОТА Построить график в полярных координатах по следующим данным: t=0,0.1,…, π; x(t)=sin(2t); y(t)=cos(2t). 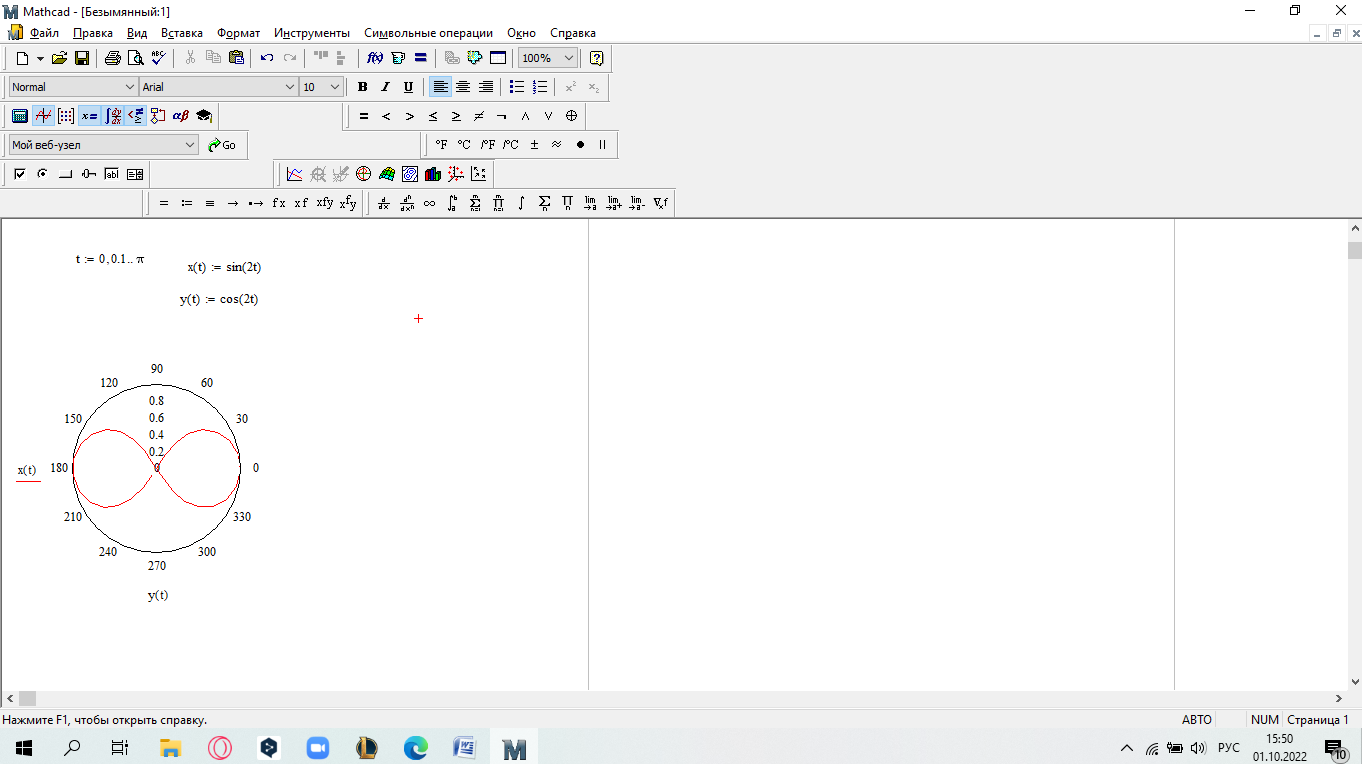 Построить график функции f(x,y)=sin(x2+y2), где x принадлежит интервалу [-1.5,1.5], y – интервалу [-1.5,1.5]. 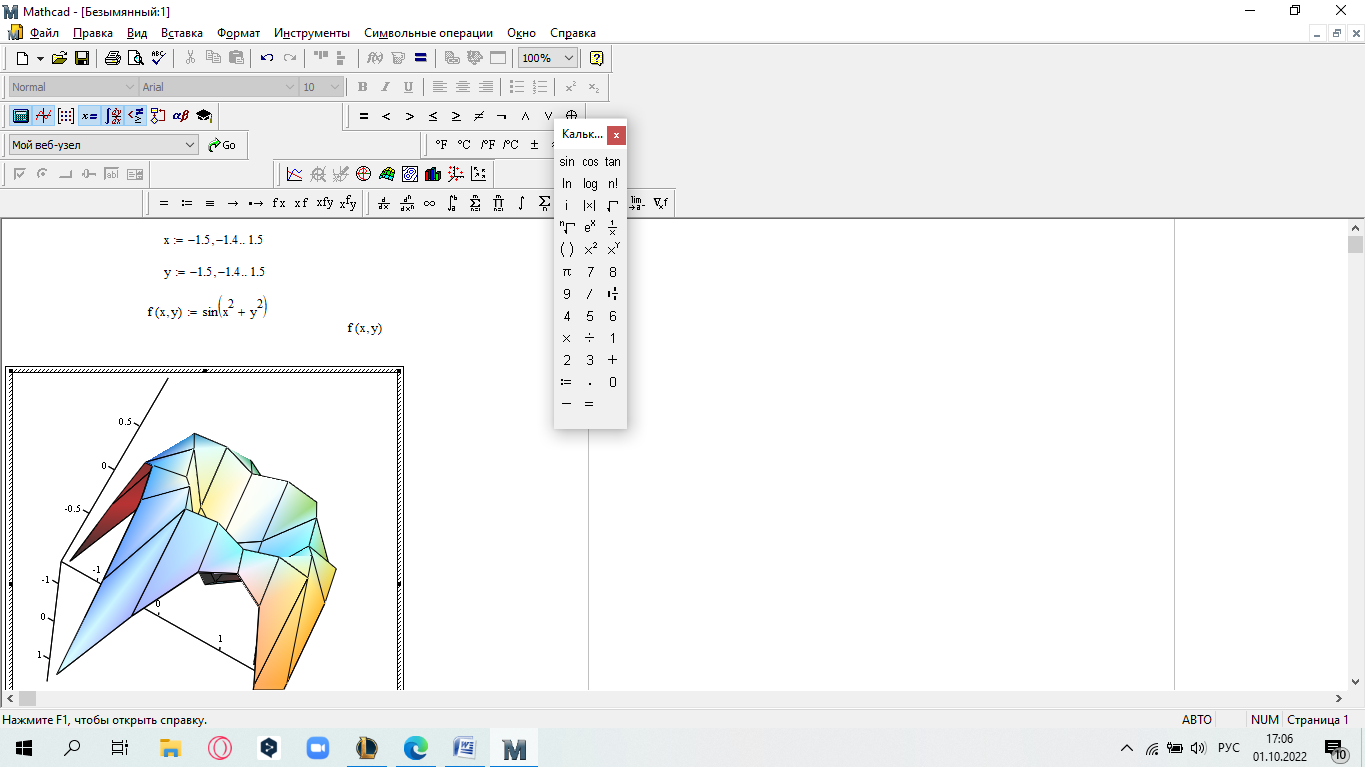 Постройте графики функций для х из интервала [-10; 10]: 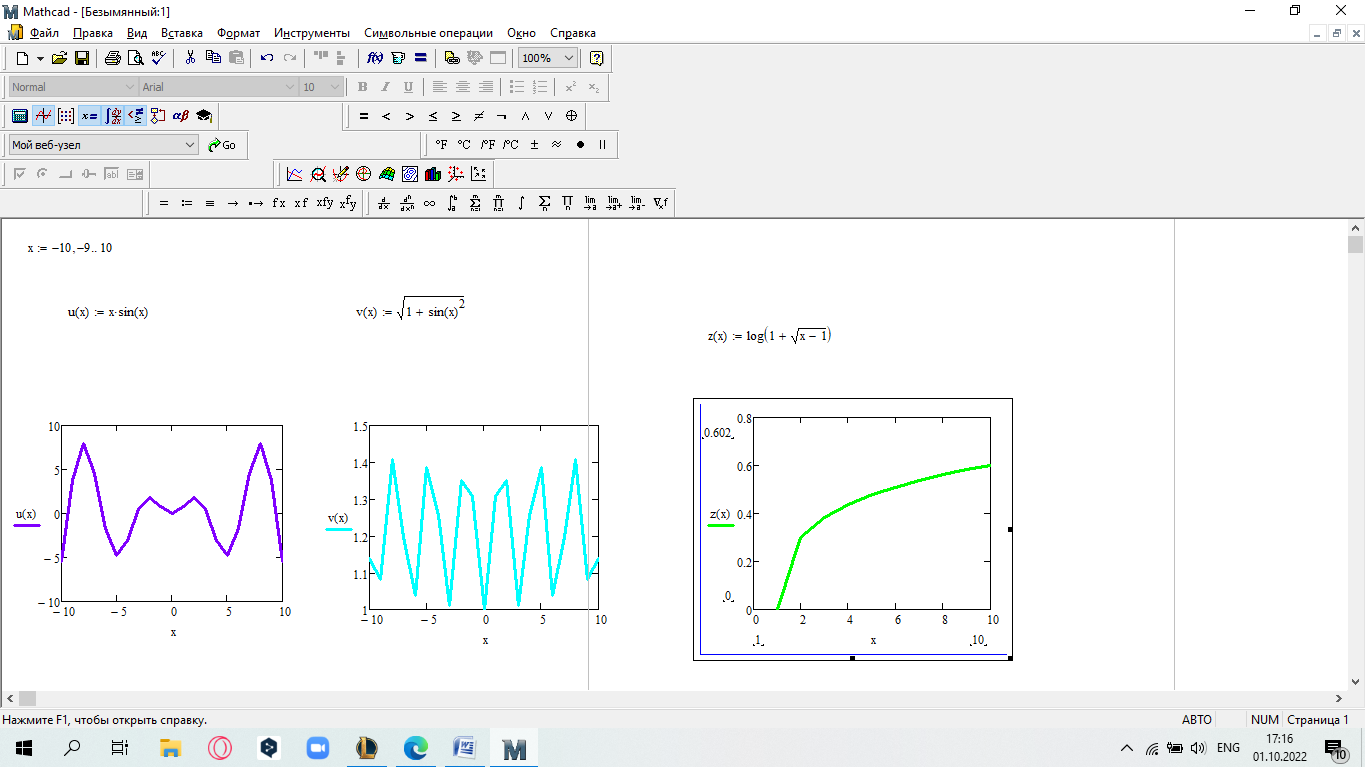 а) u(x) xsin x; б) v(x) ; в) z(x) log(1 x 1) . 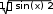  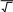 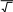 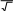 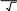 Постройте таблицу значений и графики функций f(x) и g(x) на указанном от- резке [a,b]с шагом h (таблица 2). Постройте таблицу значений и графики функций f(x) и g(x) на указанном от- резке [a,b]с шагом h (таблица 2).Таблица 2 – Данные для построения графиков функций
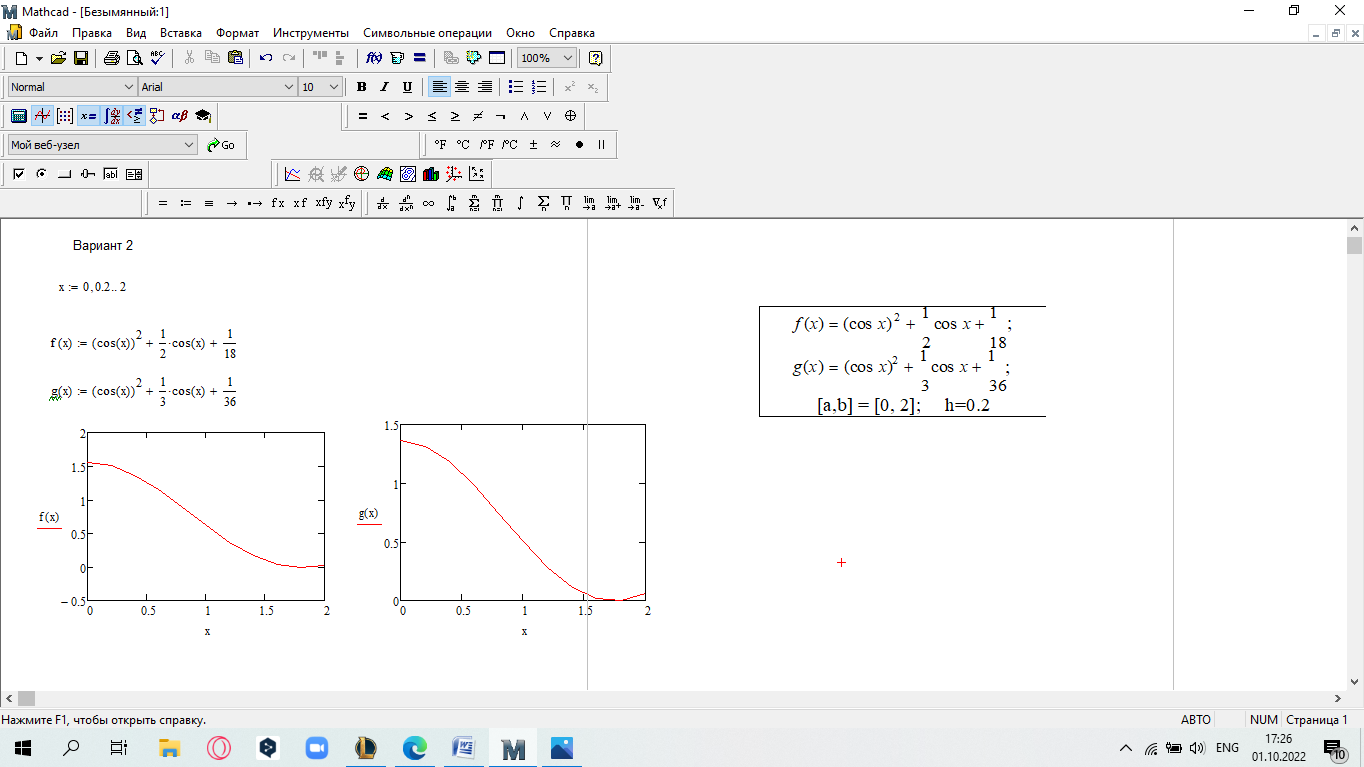 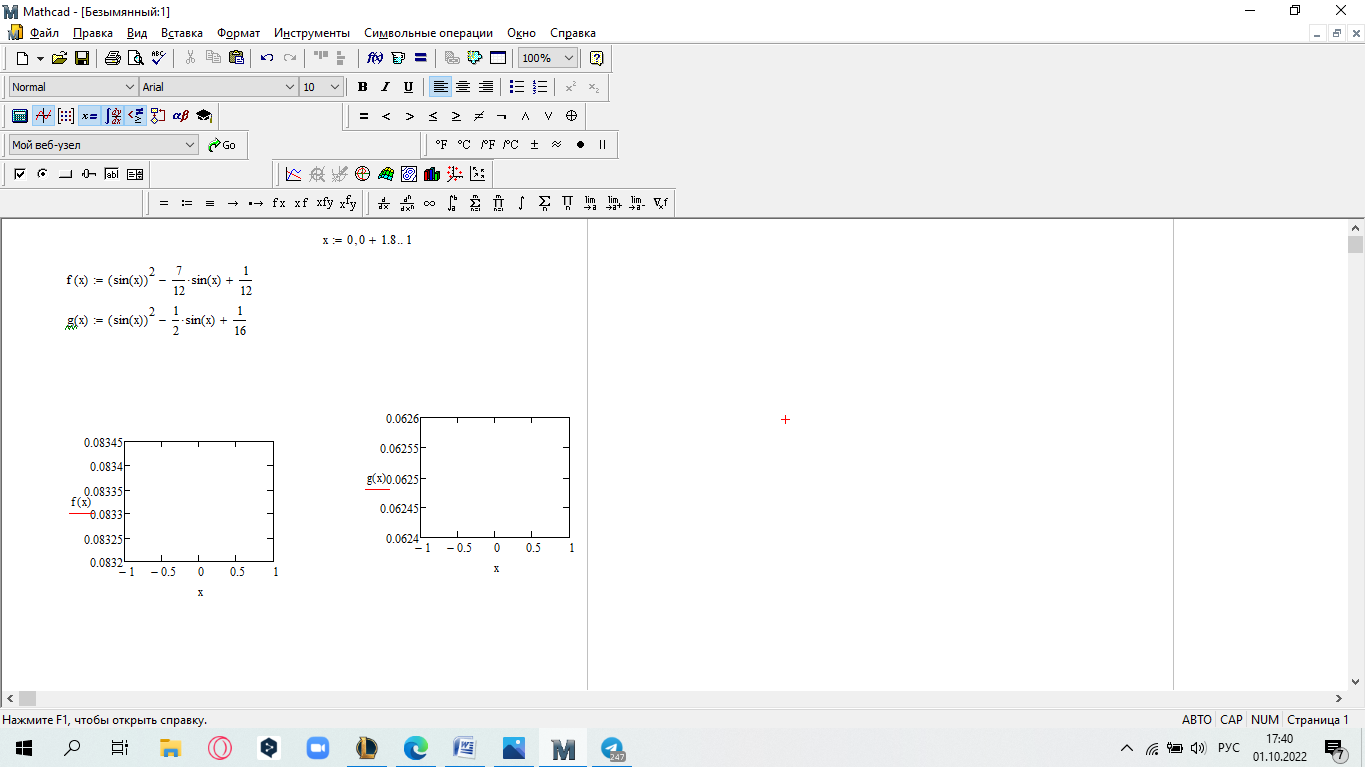 Проведите полное исследование функции f(x)(таблица 3).  Таблица 3 – Распределение заданий по вариантам Таблица 3 – Распределение заданий по вариантам
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

