1 боб. I БОБ 1параграф. I боб. Олий таълим тизимида дискрет математика фанини итишнинг назарий асослари

• Название: I боб. Олий таълим тизимида дискрет математика фанини итишнинг назарий асослари
• Анкор: 1 боб
• Дата: 20.08.2021
• Размер: 309.58 Kb.
• Имя файла: I БОБ 1параграф.docx
• Тип: Документы; #227407

I БОБ. ОЛИЙ ТАЪЛИМ ТИЗИМИДА ДИСКРЕТ МАТЕМАТИКА ФАНИНИ ЎҚИТИШНИНГ НАЗАРИЙ АСОСЛАРИ

1.1-§. Олий таълим тизимида дискрет математика фанини ўқитишнинг хусусиятлари ва ҳозирги ҳолати

Математикада дискрет математика фанининг тутган ўрни беқиёс. Кўпгина математик объектларни ўрганишда, аввало уларга мос келадиган математик моделлар тузиб олинади. Замонавий компьютерларни дастурлашда ва ахборот технологияларининг назарий асосларида дискрет математика ва математик мантиқ методлари кенг қўлланилади.

Дискрет математика фани математиканинг бошқа бўлимларидан фойдаланади ва аксинча. Масалан, равшанки математик анализ, геометрия ва алгебра, алгоритмлар назарияси билан чамбарчас боғланган.

Мазкур масаланинг ҳал қилиниши билан боғлиқ вазифаларни амалга ошириш доирасида Олий таълим тизимида Дискрет математика фани ўқув мазмуни, ўқув дастурлари, адабиётлар ва соҳага оид илмий тадқиқотлар ўрганилди ва таҳлил қилинди, тажрибали ўқитувчилар билан суҳбатлар олиб борилди, ўқитувчи ва талабаларнинг фикр-мулоҳазалари ўрганилди.

Ўрганиш ва таҳлиллар асосида Олий таълим тизимида Дискрет математикани ўқитилиш сифатини янада оширишга хизмат қилишга қаратилган қатор вазифалар ҳамда ечимини кутаётган муаммолар мавжудлиги аниқланди:

Олий таълим тизимида Дискрет математикани ўқитишнинг мақсади Давлат таълим стандарти ва ўқув фан дастуридаги мақсадлар билан чекланган бўлиб, талабанинг билим ва кўникмасига қўйилган компетенция даражаси ва уларнинг хатти-ҳаракатини ҳисобга олган ҳолдаги дарс мақсадлари ишлаб чиқилмаган;

Олий таълим тизимида Дискрет математика ўқув режалари ва фан дастурлари ўқув мазмунига мувофиқ математика ўқув фанидаги дискрет математикага оид белгилаб берилган мавзуларнинг ўқитилиши замон талабида такомиллаштирилмаган;

Олий таълим тизимида Дискрет математикани назарийлаштирилган ҳолда ўқитилишига устуворлик берилган;

Дискрет математикага оид дарс жараёнлари деярли лойиҳалаштирилмаган;

Дискрет математикани ўқитишдаги дарс жараёнида талабаларнинг мустақил ишлаш кўникмасини шакллантиришга ва шу орқали уларнинг мустақил фикрлаш қобилиятларини ривожлантиришга етарлича эътибор қаратилмаган;

Дискрет математикани таълим талаблари асосида талабаларнинг қизиқиш ва эҳтиёжларидан келиб чиқиб, математикадан фан тўгаракларини ташкил этишга кучли эътибор қаратилмаган.

Дискрет математикага тавсия этилган ўқув мазмуни ва уларни ўрганиш учун тақсимланган соатлар миқдори таҳлили шуни кўрсатадики, Ўзбекистон Республикаси Олий ва ўрта махсус таълим вазирлиги, Ўрта махсус, касб-ҳунар таълими маркази ва Ахборот-методик хизмати томонидан 2017-2018 ўқув йилидан бошлаб ўқитиш учун академик лицей “Дискрет математика” фани бўйича ўқув дастурида ўқитишга жами соат: 92 соат, маъруза учун 36 соат, амалий машғулот учун 18 соат, мустақил ишга 36 соат ажратилган бўлиб, жами 92 аудитория соатини ташкил қилади.

Агарда уларнинг ўқитилиш кетма-кетлиги ва мавзуларга ажратилган соат ҳажмига эътибор қаратадиган бўлсак, бундай ҳолатда икки хил ёндашув келиб чиқади: таълим мазмуни, ҳажми ва унинг вақт тақсимотига мос ўқитишнинг методикасини таклиф этиш ёки ўқув мазмуни ва уларга ажратилган вақт тақсимотини кенгайтириш орқали ўқитиш методикасини ишлаб чиқиш. Агар биринчи ёндашувга тўхталадиган бўлсак, маъруза ва амалий дарслари қуйидагича кетма-кетликда ўқитилади:

Асосий қисм

Фаннинг назарий машғулотлари мазмуни

Дискрет математика ва математик мантик фанига кириш. Унинг фанда ва амалиётда тутган ўрни.

Тўпламлар назарияси

Тўпламлар ва улар устида амаллар. Муносабатлар. Бинар муносабатлар. Махсус бинар муносабатлар.Эквивалентлик муносабати.Тартибланган тупламлар.

Мулоҳазалар алгебраси

Алфавит. Сўз. Мантиқий боғловчилар. Формула. Қисмий формула.

Формулаларнинг тенг кучлилиги. Чинлилик жадвали. Мулохазалар алгебраси формуласининг нормал шакллари.

Буль функциялари

Уларнинг берилиш усуллари. Буль функциялари сони. Эркли ва

боғлик ўзгарувчилар. Элементар буль функциялари. Формула тушунчаси.Функцияларни формулалар кўринишда ифодалаш. Суперпозиция тушунчаси.Формулаларнинг эквивалентлиги. Элементар функцияларнинг хоссалари.Иккиламчи функциялар. Иккиламчилик принципи. Буль функцияларининг ўзгарувчилар бўйича ёйилмаси. Мукаммал дизъюнктив нормал форма.

Мукаммал конъюнктив нормал форма. Жегалкин кўпҳади. Функциялар системасининг тўлиқлиги ва ёпиқлиги. Ёпилма. Бир системанинг тўлиқлигини бошқа тўлиқ система орқали ўрнатиш. Тўлиқ системага мисоллар. Муҳим ёпиқ синфлар. Константаларни сақловчи функциялар синфи. Ўз-ўзига кушма функциялар синфи. Монотон функциялар синфи.Чизиқли функциялар синфи. Максимал синфлар. Пост теоремалари.

Аксиоматик назария

Хисоб тушунчаси. Мулоҳазалар ҳисоби. Келтириб чикариш. Исбот

тушунчаси. Исботланувчи формула таърифи. Теорема тушунчаси. Мулоҳазалар ҳисобининг аксиомалари. Дедукция теоремаси. Умумлашган дедукция теоремаси. Конъюкцияни киритиш қоидаси. Дизъюнкцияни киритиш қоидаси. Шартларнинг ўрин алмаштириш қонуни. Шартларни бирлаштириш қонуни. Шартларни ажратиш қонуни.Ҳосилавий келтириб чиқариш қоидалари. Бир вақтда ўрнига қўйиш қоидаси. Мураккаб хулоса қоидаси. Силлогизм қоидаси. Контрпозиция қоидаси. Икки марталик инкорни тушириш қоидаси.Формулаларнинг монотонлиги тушунчаси. Мантиқий амалларнинг монотонлиги ҳақидаги теоремалар. Формулаларнинг эквивалентлиги.Эквивалентлик ҳақидаги теорема. Мулоҳазалар ҳисобининг зиддиятли эмаслиги. Мулоҳазалар ҳисобининг тўлиқлиги.Мулоҳазалар ҳисоби аксиомалари системасининг эркинлиги.

Предикатлар мантиқи

Предикат (мантиқий функция) тушунчаси. Предметлар соҳаси.

Ўзгармас предметлар ва ўзгарувчи мулоҳазалар. Элементар формулалар.Предикатларнинг қийматлари.Кванторлар. Умумийлик квантори. Мавжудлик квантори. Предикатлар макнтикининг алфавити. Терм тушунчаси. Формула таърифи. Формула қиймати. Тенг кучли формулалар. Асосий тенг кучлиформулалар. Бажарилувчи формулалар. Умумқийматли формулалар. Айнан

чин формула. Айнан ёлғон формула. Мантиқ қонуни. Умумқийматли ва бажарилувчи формулалар ҳақидаги теоремалар. Предикатлар мантиқи формуласининг нормал шакли. Формуланинг деярли нормал шакли.Формуланинг нормал шакли. Ечилиш муаммоси. Чекли соҳаларда ечилиш муаммоси. Ёпиқ формула. Формуланинг умумий ёпилиши. Формуланинг мавжудлигини ёпиш. Таркибида бир турдаги квантор амали қатнашган нормал шаклдаги формулалар учун ечилиш муаммоси.

Аксиоматик предикатлар ҳисоби

Предикатлар ҳисобининг аксиомалари системаси. Умумийлик ва

мавжудлик кванторларини киритиш қоидаси. Ечилиш, зиддиятсизлик, тўлиқлилик ва эркинлик муаммолари.

Графлар назарияси. Графлар назариясининг асосий тушунчалари. Графларнинг баъзи махсус турлари.Графларнинг берилиш усуллари. Графлар устида амаллар. Қўшнилик ва инцидентлик матрицалари. Маршрутлар ва занжирлар. Графнинг боғламлилиги тушунчаси.Планар графлар.Эйлер теоремаси.Эйлер графи.Энг қисқа йўл масаласи.

Амалий машғулотларнинг тахминий тавсия этиладиган мавзулари:

1. Тўпламлар устида амаллар. Тўплам Булеани. Декарт кўпайтма.

Муносабатлар ва функциялар. Тартиб муносабати турлари.

2. Мулоҳаза тушунчаси. Ростлик жадваллари.

3. Пропозиционал форма тушунчаси. Тавтология тушунчаси.

4. Мантиқий натижалар ва мантиқий эквивалентликлар.

5. Дизьюнктив ва Коньюнктив нормал формалар. Мукаммал дизьюнктив ва коньюнктив формалар.
6. Ростлик ёки Буль функциялари. Элементар функциялар.

7. Умумий формал аксиоматик назария. Формал аксиоматик назарияларда келтириб чиқариш, теорема тушунчалари.

8. Умумий формал аксиоматик назарияларнинг ҳоссалари.

9. Мулоҳазалар алгебраси учун L формал аксиоматик назария.

10. Дедукция теоремаси. L даги келтириб чиқаришлар.

11. Гёделнинг тўлиқлик ҳақидаги теоремаси ва ундан келиб чиқадиган натижалар.

12. Предикатлар ва улар устида амаллар. Умумийлик ва мавжудлик

кванторлари.

13. Бажарилувчи ва айнан рост (тавтология) предикатлар. Предикатлар алгебрасида формула тушунчаси.

14. Баъзибир формулаларнинг эквивалентлигини кўрсатиш.

15. Предикатлар алгебрасидаги мантиқий қонунлар.

16. Предикатлар алгебраси учун формал аксиоматик назария символлари,формула тушунчаси.

17. Предмет ўзгарувчисининг формулаларга боғлиқли ва боғлиқсиз

киришлари. Термнинг берилган формула учун эркли ёки эрксиз

эканлигини аниқлаш.

18. Интерпретация ва модель тушунчалари.

19. Биринчи тартибли назария.

20. Баъзибир метатеоремалар.

Мустақил ишларнинг тавсия этиладиган мавзулари:

1. Буль функциялари. Элементар буль функциялари.

2. Функцияларни формулалар кўринишда ифодалаш.

3. Формулаларнинг эквивалентлиги.

4. Иккиламчи функциялар. Иккиламчилик принципи.

5. Функциялар системасининг тўлиқлиги ва ёпиқлиги.

6. Константа сақловчи функциялар синфи.

7. Ўз-ўзига иккиламчи функциялар синфи.

8. Монотон функциялар синфи.

9. Чизиқли функциялар синфи.

10. Функциялар системаси тўлиқлигининг зарурий ва етарли шарти.

11. Минималлаш операцияси.

12. Исботланувчи формула.

13. Ҳосилавий келтириб чиқариш қоидалари.

14. Дедукция теоремаси. Умумлашган дедукция теоремаси.

15. Мантиқий амалларнинг монотонлиги ҳақидаги теоремалар.

16. Эквивалентлик ҳақидаги теорема.

17. Мулоҳазалар алгебраси ва мулоҳазалар ҳисоби орасидаги боғланиш.

18. Мулоҳазалар ҳисобининг зиддиятли эмаслиги.

19. Мулоҳазалар ҳисобининг тўлиқлиги.

20. Мулоҳазалар ҳисоби аксиомалари системасининг эркинлиги.

21. Предикат (мантиқий функция). Бир ўринли предикат. Кўп ўринли

предикат.

22. Предикатлар мантиқи формуласининг нормал шакли.

23. Бажарилувчи формулалар. Умумқийматли формулалар. Айнан чин формула. Айнан ёлғон формула.

24. Мантиқ қонуни. Умумқийматли ва бажарилувчи формулалар ҳақидаги теоремалар.

25. Ечилиш муаммоси.

26. Аксиоматик предикатлар ҳисоби. Предикатлар ҳисобининг

аксиомалари системаси. Умумийлик ва мавжудлик кванторларини

киритиш қоидаси.

27. Ечилиш, зиддиятсизлик, тўлиқлилик ва эркинлик муаммолари.

28. Биринчи тартибли тил. Мантиқий аксиомалар. Хос аксиомалар.

Келтириб чиқариш қоидалари. Исботлаш тушунчаси. Теорема.

29. Назария тилининг интерпретацияси. Назариянинг модели.Изоморфизм.

30. Биринчи тартибли назарияда ечилиш, зиддиятсизлик ва тўлиқлик

муаммолари.

Хорижий тажрибаларнинг ютуқларини эътиборга олган ҳолда олий таълим тизимида ўқитиладиган дискрет математика фани таълим мазмунини янада кенгайтириш, турли замонавий ёндашувлар асосида ўқитиш методикасини кучайтириш зарурлигини алоҳида қайд қилиш лозим.

Бунинг учун ўқитилаётган “Дискрет математика” ўқув фани дастурлари таҳлил қилиб чиқилди (1.1-жадвалга қаранг).

1.1-жадвал.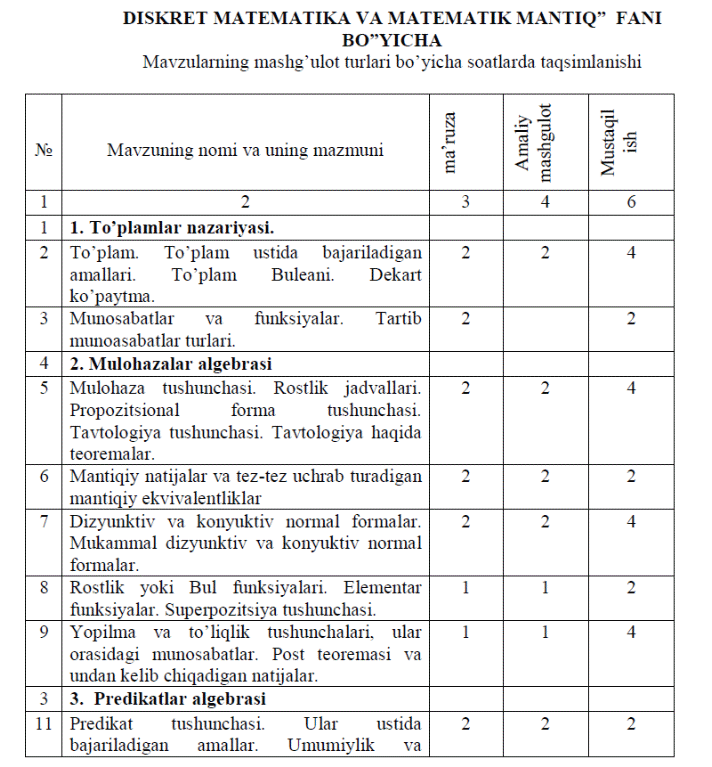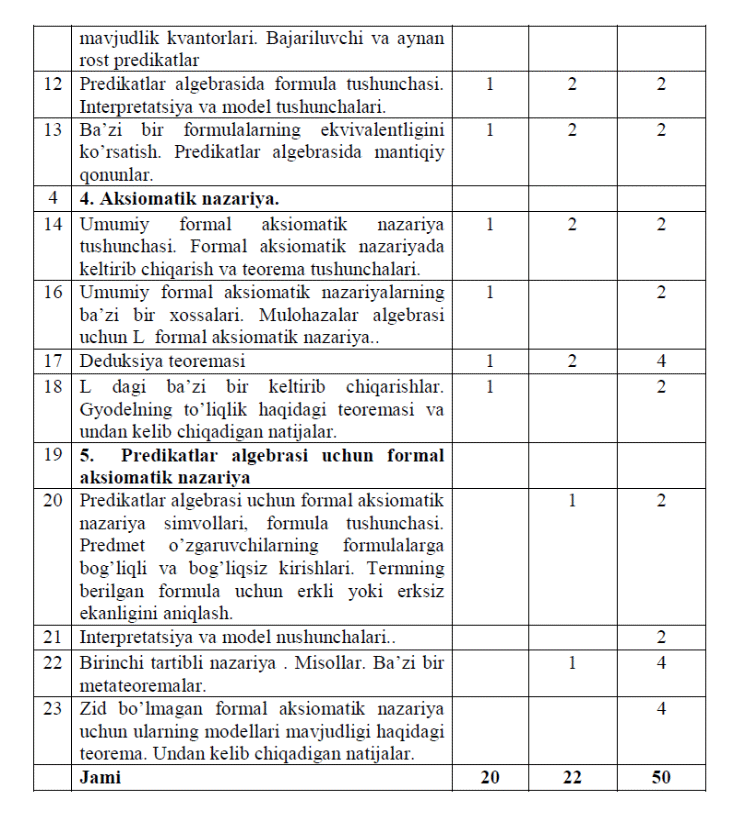





Ўзбекистон Республикаси Олий ва ўрта махсус таълим вазирлиги 2017-2018 ўқув йилидан бошлаб ўқитиш учун тасдиқланган “Дискрет Математика” ўқув фан дастурида тушунтириш хати ва мустақил иш соатлари берилган бўлиб, бўлимларнинг мазмуни юқоридагидек такрорланган.

Дискрет Математика фанини ўқитишда масаланинг аҳамияти жуда катта бўлиб, талабаларда математикага бўлган қизиқишни орттириш, таянч ва фанга оид компетенцияларни шакллантириш учун таълим жараёнида амалий ва ностандарт характердаги масалалардан фойдаланиш мақсадга мувофиқ [121;-58-60 б.]. Мулохазар алгебраси , тупламлар оркали ечиладиган масалалар, киска йулни топишга оид масалалар, реле контакт схемаларни соддалаштиришга оид масалаларга соат ажратилган. Туплам,Буль функциялари ва графлар назарияси ёрдамида табиатдаги ва фанлардаги содда ҳодиса ва жараёнларнинг математик моделларини тузиш ва таҳлил қила олиш имкониятлари юзага келади [13].

Дарс жараёнларида кузатилган камчиликлардан бири, талабалар масалаларни бир хил усулдан фойдаланган ҳолда ечишади ёки дискрет математика фанининг асосини англамасдан туриб, формулаларни шунчаки ёдлаган ҳолда (ёндафтардан фойдаланиб) тест топшириқларини бажаришади. Масалан, A {2468} , B {34567} , X {123456789} тупламлар учун AB, AB, A \ B, B \ A, A, B ларни топишда таърифдан фойдаланиб ечимга эришилади.

Фан бўйича талабаларнинг билим, кўникма ва малакасига

қўйиладиган талаблар

« Дискрет математика » ўқув фанини ўзлаштириш жараёнида амалга ошириладиган масалалар доирасида бакалавр:

- математикада дискрет математика ва математик мантиқ фанининг

тутган ўрни ва унинг ривожланиш тарихий этаплари, тўпламлар ва

улар устида амаллар, муносабатлар, мулоҳазалар, буль функциялари,

аксиоматик назария, мулоҳазалар ҳисоби, биринчи тартибли назария,

кванторлар, предикатлар мантиқи, предикатлар ҳисоби ҳақида

билиши керак;

- тўпламлар устида амаллар бажариш, ростлик жадвалидан

фойдаланиш, формулаларни мукаммал нормал шаклга келтириш,

назариялар қуриш кўникмаларига эга бўлиши керак;

- тўпламлар назарияси, мантикий фикрлаш принциплари,

формулаларнинг нормал шаклларига келтириш, “исбот”ларни қуриш,

тўлиқликни аниқлаш, назариянинг зиддиятсизлигини кўрсатиш

малакасига эга бўлиши керак;

Олий таълим тизимида таълим-тарбиянинг сифати, самарадорлиги ҳамда дискрет математикани ўқитишга оид методикани такомиллаштиришда кўпроқ эътибор қаратиш лозим бўлган қуйидаги ҳолатларнинг мавжудлиги аниқланди:

Давлат таълим стандартларида олий таълим талабаларига Дискрет математика бўйича белгиланган билим, кўникма ва малакага қўйиладиган мажбурий минимал талаблар билан ўқув дастурларидаги таълим мазмунининг мувофиқлик ҳолати;

амалдаги ўқув дастурларда Дискрет математика учун ажратилган соатлар тақсимотининг ўқув мазмунини ўрганиш учун мувофиқлиги ҳолати ҳамда тушунчаларнинг изчиллиги, узвийлиги, бирлиги каби тамойилларни эътиборга олиниши билан боғлиқ ҳолатлар.

Шуни таъкидлаш лозимки, ўқув материалини баён этишда таянч тушунчаларни етарли даражада аниқ ва содда тарзда тушунтириш ҳал қилувчи аҳамиятга эга. Албатта, бунда ўқитувчи асосий ғоялар ва натижаларни маълум даражада эркин беришга мажбурдир.

“Дискрет Математика” ўкув фан дастурига асосан барча теоремаларнинг ва фактларнинг исботини бермасдан, уларнинг исботидаги мантиқий ва когнитив томонларига эътиборни кучайтириш тавсия этилди [13].

Университетлар учун Дискрет математика фанини лойиҳалаб ўқитиш методикасини такомиллаштириш бўйича таклифлар ишлаб чиқиш ва асослаш муҳим аҳамиятга эга.

Шундай қилиб, Олий таълим тизимида Дискрет математик фанини ўқитишни такомиллаштириш бўйича таклиф ва тавсиялар ишлаб чиқилди. Хусусан: Олий таълим тизимида Дискрет математикини ўқитиш натижасида талабаларда олган билимларни кундалик фаолиятда қўллаш, келажакда касбий фаолияти учун зарур бўлган математик билим ва кўникмалар тизимини шакллантириш, малакаларни ривожлантириш;

жадал тараққий этаётган жамиятимизда муваффақиятли фаолият юрита оладиган, танқидий ҳамда мантиқий фикрлай оладиган баркамол шахсни шакллантириш;

талабаларда миллий, маънавий ва маданий меросни қадрлаш кўникмасини шакллантириш, умумбашарий маданиятнинг таркибий қисми сифатида математик маданиятни тарбиялаш;

ўқитувчининг йўналтирувчилик фаолияти асосида дарс жараёнининг ўзида талабаларнинг муайян мавзу устида мустақил ишлаш кўникмасини шакллантириш;

теоремаларни мантиқий исботлаш кўникмасини шакллантиришда таянч тушинчалар аҳамиятини билиш орқали талабаларни онгли равишда келгуси фанларни узлаштиришни таъминлаш.