эл. учебник. И фундаменты

• Название: И фундаменты
• Дата: 21.10.2022
• Размер: 1.24 Mb.
• Имя файла: эл. учебник.doc
• Тип: Учебник; #746623
• страница: 7 из 26

И

2

i-l

5>

(-1

где п — число отсеков, на которые разбивается призма AC; rpu — расчет­ный угол внутреннего трения грунта на (-м участке поверхности скольже­ния; си — расчетное удельное сцепление грунта на i-uучастке поверхности скольжения; /j — длина 1-го участка окружности; F_t—вес сдвигающей приз­мы (левой); Ff—вес удерживающей призмы (правой); остальные обозначен кия те же, что на рис, 10.13,

Для нахождения наиболее опасной поверхности скольжения задаются системой центров вращения обычно на пересечении трех горизонталей с. тремя вертикалями. Производят девять по­строений, аналогичных рис. 10.13, и находят минимальное зна­чение г), как это делается при расчете устойчивости откосов (рис. 8.10). Оно должно удовлетворять условию

(10.21)

> Yn/Yc-

где у_п— коэффициент надежности; у_с— коэффициент условий работы. 246

					t
27/ /	/ ill /if .Ш la				ш ш ш ш »i >.,
ч							v W
It 1			•1			[ и
*|			. *		Л'
\

Рис. 10.14. Расчетная схема фунда­мента, работающего на выдергивание

Если это условие не удов­летворяется, изменяют основ­ные размеры фундамента.

При определении M_rtи M_sпринимают одинаковое значе­ние удельного веса грунта, а также учитывают взвешиваю­щее действие грунтовой воды.

Фундамент, работающий на выдергивание при сравнительно мелком заложении также рассчитывается по I группе предель­ных состояний по устойчивости (рис. 10.14). _Li Коэффициент запаса устойчивости в таком случае

где Eat— расчетное активное давление грунта по вертикальным поверхно­стям, проходящим по контуру подошвы фундамента; ф_г—расчетный угол внутреннего трения грунта; остальные обозначения прежние.

Сумма SjE'aitgqPi соответствует сопротивлению сдвигу по вертикальным поверхностям, проходящим по контуру подошвы фундамента.

Анкерная плита должна иметь арматуру в верхней части (см. рис.10.14). Нижняя арматура устанавливается, если сила /V_Ot меняет направление,

10.3. Основные положения

проектирования гибких фундаментов

10.3.1. Общие положения

На распределение давления под гибкими фундаментами влияет их деформация, а иногда и деформация системы надзем­ных конструкций с фундаментами. В связи с этим на усилия в конструкции гибкого фундамента влияет его жесткость, жест­кость основания и жесткость надземных конструкций.

В зависимости от протяженности гибких фундаментов разли­чают плоскую задачу, когда фундамент (например, ленточный под стену) в каждом сечении по его длине имеет одинаковую форму деформации (рис. 10.15,а), и пространственную задачу в двух случаях: 1) балка на упругом основании (ленточный фундамент под колонны, принимаемый в поперечном направле­нии жестким, рис, 10,15,6); 2) фундаментная плита на упругом

247
Рис. 10.15. Расчетные схемы гибких фундаментов в случае упругого полу*

пространства

основании (когда в обоих направлениях учитывается искрив­ление фундамента, рис. 10.15, а). Фундаментные плиты могут быть сплошные, ребристые и коробчатые.

10.3.2. Основные расчетные модели оснований

Известно много методов расчета балок на упругом осно­вании, применяемых к линейно деформируемым грунтам. Наи­большее распространение получили следующие теории:

местных деформаций с постоянным коэффициентом постели;

местных деформаций с переменным коэффициентом постели;

упругого полупространства;

упругого слоя на несжимаемом основании;

упругого слоя с переменным модулем деформации грунтов в основании по глубине.

Кроме того, в настоящее время применяют численные мето­ды^ позволяющие учитывать совместно деформации основания, фундаментов и надземных конструкций.

Теория местных деформаций предложена для расчета на из­гиб шпал Вииклером (1867 г.). Исходит из основного положе­ния, выдвинутого русским академиком Н. И. Фуссом в 1801 г.: реакция грунта основания в каждой точке подошвы фундамента (балки) прямо пропорциональна осадке этой точки, т. е.

_Py*=C_zZ,(10.22)

где C_z — коэффициент постели (упругого сжатия основания); Z— осадка в месте определения реакции грунта p_s.

Схему такого основания можно представить в виде пружин (рис. 10.16, а). За пределами балки поверхность грунта не по­лучает деформации.

Теория упругого пространства является другой крайней тео­рией расчета балок и плит на упругом основании. В этом случае фундаментная балка принимается лежащей на однородном уп­ругом или линейно деформируемом бесконечном полупростран­стве (рис. 10.16,6"). Эта теория была выдвинута Г. Э. Прокто-

248

в)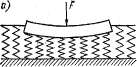



Рис. 10.16. Схемы упругого основания

ром и развита Н, М. Герсеваыовым, М. И. Горбуновым-Посадо-вым, Б. Н. Жемочкиным, И. А. Симвулнди, А. П. Синицыным и др.

Наблюдения многих исследователей показали, что деформа­ции за пределами площади загружения затухают значительно быстрее, чем согласно теории бесконечного полупространства. Исследования ЛИСИ * свидетельствуют, что основные деформа­ции уплотнения грунта развиваются в пределах сравнительно небольшой глубины, а ниже происходят лишь упругие деформа­ции, составляющие около 5 % величины осадки (рис. 10.17). Последние деформации обусловлены упругими деформациями грунта. Это подтверждает целесообразность использования тео­рии упругого (линейно деформируемого) слоя иа несжимаемом основании.

Дополнительным подтверждением являются результаты на­блюдений за осадкой поверхности грунта и осадкой глубинных марок, полученные С. Н. Сотниковым и А. А. Собениным в ЛИСИ. Эти наблюдения и анализ их результатов показали, что поверхность грунта вблизи возводимых зданий деформируется приблизительно в соответствии с деформацией поверхности слой линейно деформируемого грунта, лежащего на упругом основании, имеющем модуль упругости в 10...20 раз больший модуля общих деформаций.

Теория расчета балок на упругом (линейно деформируемом) слое грунта конечной толщины развита М. И. Горбуновым-Поса-довым, С. С. Давыдовым, Г. В. Крашенинниковой, И. К- Самари­ным, О. Я- Шихтер и др. Основной сложностью использования этой теории является установление толщины деформируемого слоя. По-видимому, это можно сделать, руководствуясь способом определения расчетной мощности сжимаемой толщи при расчете осадки фундаментов методом ограниченной сжимаемой толщи (см. п. 7.4).

* Далматов Б. И., Голли А. В. Устройство для измерения деформаций и напряжений в основании штампов//Механика грунтов, основания и фунда­менты: Материалы XXIX научной конференции ЛИСИ, Л„ 1970,

Ё49

Рис. 10.17. Распределение послойных

перемещений по глубине основания из

суглинка

/ — перемещения полные при загрузке жест­кого штампа; 2 — перемещения упругие с упругим последействием при разгрузке штампа

Исследования, выполненные в ЛИСИ В. М. Чикишевым, пока­зали, что в однородных суглин­ках изменение модуля деформа­ции по глубине можно принять по гиперболической зависимо­сти. В то же время исследова­ния В. М. Чикишева, а также А. В. Голли свидетельствуют, что правильнее рассматривать комбинированное основание, учитывающее упругие деформации в пределах полупространства и остаточные деформации сжатия грунта по толщине ограниченного слоя. В пределах этого слоя может быть учтена и переменность модуля деформации по глу­бине. Использование такой расчетной модели возможно при решении задачи методом конечных элементов.

Параллельно с развитием теорий расчета балок на упругом (линейно деформируемом) полупространстве и слое грунта со­вершенствовалась теория местных деформаций. С целью при­ближения этой теории к реальным условиям работы ленточных фундаментов, включая учет совместной работы сооружения с основанием, стали принимать переменное значение коэффи­циента постели по длине балки или сооружения. Если известна жесткость (податливость) основания в каждой точке по длине балки (ленточного фундамента), ■ то определение реактивных давлений не представляет больших затруднений. Поэтому та­кой метод и вошел в практику проектирования. Вся сложность задачи сводится к правильному определению закона изменения коэффициента постели по длине балки. Учет неоднородности основания по отдельным скважинам не может дать требуемой точности определения усилий, возникающих в фундаменте, так как при этом не рассматривается пространственная работа грунта.

Таким образом, из рассмотрения развития методов расчета балок и плит на упругом основании видно, что эти методы нуж­даются в дальнейшей разработке в соответствии с законами диалектики.

10.3.3. Некоторые рекомендации к расчету

фундаментов на упругом основании

Как показали исследования Г. В. Крашенинниковой, ме­тод местных деформаций с постоянным коэффициентом достели

250

при плоской задаче дает достаточно хорошие результаты при толщине сжимаемого слоя менее //16 (где / — длина балки, рас­считываемой как плоский элемент). Метод упругого полупро­странства применим, когда постоянство модуля деформации рас­пространяется на глубину 11. В остальных случаях рекомендует­ся вести расчет балок исходя из рассмотрения деформаций уп­ругого слоя.

При слоистом залегании грунтов модуль общей деформации грунта можно осреднять аналогично коэффициенту относитель­ной сжимаемости [см. формулы (7.27) и (7.28)] по формуле •

где Н_с— расчетная величина сжимаемой толщи; п — число слоев в деформи­руемой толще; Et — модуль деформации i-ro слоя грунта; Ы — толщина i-то слоя грунта; z/ — расстояние от нижней границы сжимаемой толщи до се­редины i-ro слоя грунта.

Получаемые расчетом балок на упругом основании резуль-таты при плоской задаче в значительной степени зависят от соотношения жесткости балки и основания. В зависимости от указанного соотношения М. И. Горбунов-Посадов * считает балку при плоской задаче жесткой, когда

t« 10 (£„/£,) (P/h¹) < 1, (10.24)

где Et> — модуль деформации грунта; £\ — модуль упругости материала бал­ки (полосы); I— полудлииа балки; h— ее высота.

Зная t, по таблицам, составленным М. И. Горбуновым-Поса-довым для бесконечного полупространства, и по таблицам, со­ставленным Г. В. Крашенинниковой и И. К. Самариным для ограниченного слоя грунта при различных загрузках, можно получить значения реактивных давлений по длине рассматри­ваемой балки при плоской задаче.

Более универсальным является метод Б. Н. Жемочкина и А. П. Синицына **. Он сводится к следующему. Между рассмат­риваемой балкой и упругим (линейно деформируемым) основа­нием вводятся жесткие стержни, через которые балка опирает­ся на поверхность основания. Затем эти стержни заменяются неизвестными силами. Для балки составляется система канони­ческих уравнений, и в эту систему вводятся уравнения равно­весия. Решение системы уравнений с помощью ЭВМ позволяет определить реактивные силы, которые распределяются равно-

* Горбунов-Посадов М. И. Расчет конструкций на упругом основании, М.: Госстройиздат, 1963.

•* Жемочкин Б. Н., Сииицын А. П. Практические методы расчета фунда­ментных балок и плит па упругом основании (без гипотезы Винклера). М.; Стройиздат, 1947,

251

мерно на отдельных участках по длине балки. Этот метод при- меним как к упругому полупространству, так и к линейно де­формируемому слою. Найдя распределение реактивных сил по длине балки, легко определить в любом сечении изгибающие моменты и перерезывающие силы, по которым уточняются раз- меры сечения балки. Если при уточнении размеров сечения су- щественно меняется жесткость балки, расчет повторяют.

При предварительном подборе сечения балки на упругом основании обычно принимают равномерное или трапециевидное распределение давления по подошве. Уточнение размеров сече­ния, главным образом арматуры, выполняют после детального расчета.

Методы расчета балок и плит на упругом основании рас­смотрены в строительной механике.

П. СВАЙНЫЕ ФУНДАМЕНТЫ

11.1. Типы свай и виды свайных фундаментов

11.1.1. Типы свай

При наличии в верхней части основания слабых грунн тов обычно возникает необходимость в передаче давления со­оружения на более плотные грунты, залегающие на некоторой глубине, иногда довольно значительной. В таких случаях часто устраивают фундаменты из свай, свай-оболочек, оболочек и свай-столбов. Все эти устройства являются длинными стерж­нями, погруженными в грунт в готовом виде или изготовленными в грунте и предназначенными для передачи давления со­оружения на грунт основания. Для краткости изложения все

₁

эти устройства будем называть сваями.

'IIШ III"

_Щ

'// III ill III lil '.'I

По характеру передачи давле­ния сооружения на основание -раз­личают сваи-стойки и сваи трения (висячие) (рис. 11.1).

Щ Щ

Сваи-стойки прорезают всю толщу сжимаемых грунтов и опи­раются на слой практически несжи­маемого грунта (обычно на скаль-, ную породу). Так как сваи-стойки опираются на несжимаемый грунт,

Сшя