
Рисунок 4л.2 - Последовательность случайных моментов закона
надежности времени, в которое происходят отказы
График экспоненциального закона надежности показан на рисунке 4л.1. Для этого закона функция распределение времени безотказной работы имеет вид:
F(t)=q(t)=1-e-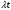 , (4л.2) , (4л.2)
а плотность -
f(t)= 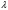 е- е-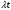 , (t>0). (4л.3) , (t>0). (4л.3)
Это есть уже известный нам показательный закон распределения, по которому распределено расстояние между соседними событиями в простейшем потоке с интенсивностью 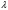 . .
При рассмотрении вопросов надежности часто бывает удобно представить себе дело так, словно на элемент действует простейший поток отказов с интенсивностью 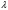 ; элемент оказывается в момент, когда происходит первое событие этого потока. ; элемент оказывается в момент, когда происходит первое событие этого потока.
Образ "потока отказов" приобретает реальный смысл, если отказавший элемент немедленно заменяется новым (восстанавливается). Последовательность случайных моментов времени, в которое происходят отказы (рисунок 4л.2), представляет собой простейший поток событий, а интервалы между событиями - независимые случайные величины, распределенные по показательному закону
Понятие "интенсивность отказов" может быть введено не только для экспоненциального, но для любого другого закона надежности с плотностью f(t); вся разница будет в том, что при не экспоненциальном законе р(t) интенсивность отказов 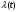 будет уже не постоянной величиной, а переменной. будет уже не постоянной величиной, а переменной.
Интенсивностью (или иначе "опасностью") отказов называется отношение плотности распределения времени безотказной работы элемента к его надежности:
 (4л.4) (4л.4)
Поясним физический смысл этой характеристики. Пусть одновременно испытывается большое число N однородных элементов, каждый - до момента своего отказа. Обозначим n(t) - число элементов, оказавших на малом участке времени (t, t+ t) t)
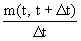 . (4л.5) . (4л.5)
На единицу времени придется среднее число отказов.
Разделим эту величину не на общее число испытываемых элементов N, а на число исправных к моменту t элементов n(t). Нетрудно убедиться, что при большом N отношение будет приближенно равно интенсивности отказов 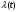 : :
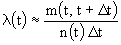 (4л.6) (4л.6)
Действительно, при большом N
n(t)  Np(t) (4л.7) Np(t) (4л.7)
и
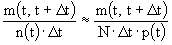 (4л.8) (4л.8)
Но согласно формуле (4л.6)
 (4л.9) (4л.9)
откуда
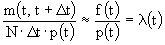 (4л.10) (4л.10)
В работах по надежности приближенное выражение (4л.10) часто рассматривают как определение интенсивности отказов, т.е. определяют как среднее число отказов в единицу времени, приходящееся на один рабочий элемент.
Характеристике 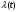 можно дать еще одно истолкование: это есть условная плотность вероятности отказа элемента в данный момент времени t, при условии, что до момента t он работал безотказно. Действительно, рассмотрим элемент вероятности можно дать еще одно истолкование: это есть условная плотность вероятности отказа элемента в данный момент времени t, при условии, что до момента t он работал безотказно. Действительно, рассмотрим элемент вероятности 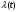 dt - вероятность того, что за время (t, t+dt) элемент перейдет из состояния "работает" в состояние "не работает", при условии, что до момента t он работал. В самом деле, безусловная вероятность отказа элемента на участке (t, t+dt) равна f(t)dt. Это - вероятность совмещения двух событий: dt - вероятность того, что за время (t, t+dt) элемент перейдет из состояния "работает" в состояние "не работает", при условии, что до момента t он работал. В самом деле, безусловная вероятность отказа элемента на участке (t, t+dt) равна f(t)dt. Это - вероятность совмещения двух событий:
А - элемент работал исправно до момента t;
В - элемент отказал на участке времени (t, t+dt).
По правилу умножения вероятностей:
f(t)dt = P(АВ) = Р(А) Р(В/А). (4л.11)
Учитывая, что Р(А)=р(t), получим:
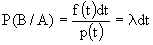 (4л.12) (4л.12)
а величина 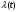 есть не что иное, как условная плотность вероятности перехода от состояния "работает" в состояние "отказал" для момента t. есть не что иное, как условная плотность вероятности перехода от состояния "работает" в состояние "отказал" для момента t.
Если известна интенсивность отказов 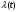 , то можно выразить через ее надежность р(t). Учитывая, что f(t)=-p'(t), запишем формулу (4л.12) в виде: , то можно выразить через ее надежность р(t). Учитывая, что f(t)=-p'(t), запишем формулу (4л.12) в виде:
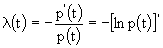 (4л.13) (4л.13)
Интегрируя, получим:
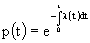 (4л.14) (4л.14)
откуда
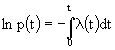 (4л.15) (4л.15)
Таким образом, надежность выражается через интенсивность отказов. В частном случае, когда 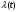 = =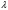 = const, формула (4л.14) дает: = const, формула (4л.14) дает:
p(t)=e-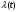 , (4л.16) , (4л.16)
т.е. уже известный нам экспоненциальный закон надежности.
Пользуясь образом "потока отказов", можно истолковать не только формулу (4л.14), но и более общую формулу (4л.16). Представим себе (совершенно условно!), что на элемент с произвольным знаком надежности p(t) действует поток отказов с переменной интенсивностью 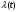 . Тогда формула (4л.16) для р(t) выражает вероятность того, что на участке времени (0, t) не появиться не одного отказа. . Тогда формула (4л.16) для р(t) выражает вероятность того, что на участке времени (0, t) не появиться не одного отказа.
Таким образом, как при экспоненциальном, так и при любом другом законе надежности, работу элемента, начиная с момента включения t=0, можно представить себе так, что на элемент действует пуассоновский закон отказов; для экспоненциального закона надежности этот поток будет с постоянной интенсивностью 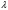 , а для не экспоненциального - с переменной интенсивностью , а для не экспоненциального - с переменной интенсивностью 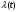 . .
Заметим, что этот образ годится только в том случае, когда отказавший элемент не заменяется новым. Если, как мы это делали раньше, немедленно заменять отказавший элемент новым, поток отказов уже не будет пуассоновским. Действительно, интенсивность его будет зависеть не просто от времени t, прошедшего с начала всего процесса, а и от времени t, прошедшего со случайного момента включения именно данного элемента; значит, поток событий имеет последствие и пуассоновским не является.
Если же на протяжении всего исследуемого процесса данный элемент не заменяется и может отказать не более одного раза, то при описании процесса, зависящего от его функционирования, можно пользоваться схемой Марковского случайного процесса, но не при переменной, а при постоянной интенсивности потока отказов.
|
 Скачать 388.57 Kb.
Скачать 388.57 Kb.