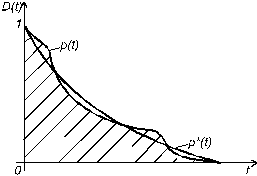
Если не экспоненциальный закон надежности сравнительно мало отличается от экспоненциального, то можно, в целях упрощения, приближенно заменить его экспоненциальным (рисунок 4л.3). Параметр 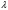 этого закона выбирается так, чтобы сохранить неизменным математическое ожидание времени безотказной работы, равное, как мы знаем, площади, ограниченной кривой p(t) и осями координат. Для этого нужно положить параметр этого закона выбирается так, чтобы сохранить неизменным математическое ожидание времени безотказной работы, равное, как мы знаем, площади, ограниченной кривой p(t) и осями координат. Для этого нужно положить параметр 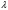 показательного закона равным, показательного закона равным,
(4л.17)
где - площадь, ограниченная кривой надежности p(t).
Таким образом, если мы хотим характеризовать надежность элемента некоторой средней интенсивностью отказов, нужно в качестве этой интенсивности взять величину, обратную среднему времени безотказной работы элемента.
Выше мы определили величину как площадь ограниченную кривой р(t). Однако если требуется знать только среднее время безотказной работы элемента, проще найти его непосредственно по статическому материалу как среднее арифметическое всех наблюдаемых значений случайной величины T - времени работы элемента до его отказа. Такой способ может быть применен и в случае, когда число опытов не велико и не позволяет достаточно точно построить кривую р(t).
Рисунок 4л.4 - Линейный закон распределение 
Рисунок 4л.5 - График функции 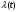
Контрольные вопросы:
Как выражаются основные параметры P(t), F(t), f(t) при экспоненциальном законе надежности?
Что называют интенсивностью отказов?
Какова зависимость между надежностью и интенсивностью отказов?
Чему равна интенсивность отказов при экспоненциальном законе?
Л.: [5] С. 18-21; [7] С. 15-16; [8] С. 11-12;
Лекция 5. Надежность нерезервированного элемента системы управления
План лекций
Надежность простой системы, составленной из независимых элементов
Общая интенсивность отказов при "последовательном "соединении"?
Определение количественные характеристики надежности нерезервированной системы
Пусть некоторая техническая система S составлена из n элементов узлов: Э1, Э2, … Эn.
Допустим, что надежности элементов нам известны. Возникает вопрос об определении надежности системы. Она зависит от того, каким образом элементы объединены в систему, какова функция каждого из них и в какой мере исправная работа каждого элемента необходима для работы системы в целом.
В ряде систем недостаточная надежность элементов повышается за счет их дублирования (резервирования). Резервирование состоит в том, что наряду с элементом Эi в систему вводится запасной резервный элемент Эi’, на который система переключается в случае отказа основного элемента. Число резервных элементов может быть и более одного.
Самым простым случаем в расчетном смысле является простая система (или система без резервирования). В такой системе отказ любого элемента равносилен отказу системы в целом. По аналогии с цепочкой последовательно соединенных проводников, обрыв каждого из которых равносилен размыканию всей цепи, мы будем называть такое соединение “последовательным”(рисунок 5л.1). Следует оговориться, что “последовательным” такое соединение элементов является только в смысле надежности, физически же они могут быть соединены как угодно.
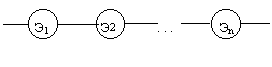
Рисунок 5л.1 - Последовательное соединение элементов
Выразим надежность простой системы через надежность ее элементов. Пусть имеется некоторый требуется обеспечить промежуток времени (0,  ), в течение которого безотказную работу системы. Тогда, если надежность системы характеризуется законом надежности P(t), нам важно знать значение этой надежности при t = ), в течение которого безотказную работу системы. Тогда, если надежность системы характеризуется законом надежности P(t), нам важно знать значение этой надежности при t =  , т.е. P( , т.е. P( ). Это не функция, а определенное число; отбросим аргумент ). Это не функция, а определенное число; отбросим аргумент  и обозначим надежность системы просто P. Аналогично обозначим надежности отдельных элементов p1, p2, …, pn. и обозначим надежность системы просто P. Аналогично обозначим надежности отдельных элементов p1, p2, …, pn.
Для безотказной работы простой системы в течение времени t нужно, чтобы работал безотказно каждый из ее элементов. Обозначим: S - событие, состоящее в безотказной работе системы за время t.
Э1, Э2, ….Эn - события, состоящие в безотказной работе соответствующих элементов. Событие S есть произведение (совмещение) событий Э1, Э2, ….Эn:
S = Э1, Э2, ….Эn. (5л.1)
Предположим, что элементы Э1, Э2, ….Эn отказывают независимо друг от друга (или, как мы будем говорить для краткости, “независимы по отказам”, а совсем кратко “независимы”). Тогда, по правилу умножения вероятностей для независимых событий
P(S) = P(Э1) P (Э2) … P (Эn), (5л.2)
или в других обозначениях,
Р = р1 *р2*…*рn, (5л.3)
а короче
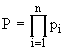 (5л.4) (5л.4)
т.е. надежность простой системы, составленной из независимых элементов, равна произведению надежности ее элементов.
В частном случае, когда все элементы обладают одинаковой надежностью
р1 =р2 = … = рn= р, (5л.5)
формула (5л.4) принимает вид:
Р = рn. (5л.6)
Контрольные вопросы:
Чему равна надежность простой системы, составленной из независимых элементов?
Из чего состоит общая интенсивность отказов при последовательном "соединении"?
Л.: [9] С. 18-21; [10] С. 24-25; [11] С. 26-27;
Лекция 6. Надежность резервированного элемента системы управления
План лекций
Надежность резервированной системы
Общая интенсивность отказов при резервированной системы
Определение количественные характеристики надежности резервированной системы
“Горячий резерв”. Одним из путей повышения надежности системы является введение в нее дублирующих (резервных элементов). Резервные элементы включаются в систему как бы “параллельно” тем, надежность которых недостаточна.
Рассмотрим самый простой пример резервированной системы: два “параллельно” включенных элемента Э1 и Э2 (Рисунок 6л.1). Вначале работает основной элемент Э1; если он отказал, система автоматически переключается на “резервный” элемент Э2. Предположим, что элементы Э1 и Э2 независимы по отказам и что их надежности (вероятности безотказной работы) за интересующее нас время t =  равны соответственно р1 и р2. Предположим также, что надежность второго элемента не зависит от того, включался ли этот элемент в работу за время равны соответственно р1 и р2. Предположим также, что надежность второго элемента не зависит от того, включался ли этот элемент в работу за время  и когда включался. Такая картина наблюдается, например, если элемент Э2 независимо от того, работает он или нет, держится под рабочим напряжением (так называемый “горячий резерв”). и когда включался. Такая картина наблюдается, например, если элемент Э2 независимо от того, работает он или нет, держится под рабочим напряжением (так называемый “горячий резерв”).
Определим при этих условиях надежность резервированной системы S. Перейдем к вероятности противоположного события – отказа системы S. Обозначим отказ системы . Чтобы событие произошло, необходимо, чтобы отказали оба элемента: и первый и второй:
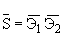 (6л.1) (6л.1)
Отсюда по правилу умножения вероятностей независимых событий:
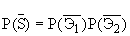 (6л.2) (6л.2)
Обозначим надежность системы Q, а надежности элементов q1, q2, получим:
Q = q1 q2, (6л.3)
т.е. при “параллельном” соединении независимых элементов их ненадежности перемножаются.
Переходя в формуле (6л.3) от ненадежностей к надежностям, имеем:
1–Р=(1–р1)(1–р2), (6л.4)
откуда
Р=1-(1-р1)(1-р2). (6л.5)
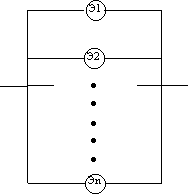 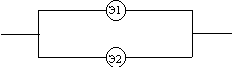
Рисунок 6л.1 - Резервированная система

Рисунок 6л.2 - Система состоящих из n дублирующих друг друга независимых элементов
При произвольном числе n дублирующих друг друга независимых элементов надежность блока из таких элементов (Рисунок 6л.2) вычисляется по формуле
Р=1-(1-р1)(1-р2)...(1-рn), (6л.6)
или, короче
Р=1-(1-р1). (6л.7)
В частном случае, когда надежности всех элементов одинаковы:
р1=р2=…=р, (6л.8)
формула (6л.7) принимает вид:
Р=1-(1-р)n. (6л.9)
“Холодный” и “облегченный” резерв. До сих пор мы рассматривали только случай, когда надежность каждого дублирующего элемента не зависит от того, когда включился в работу этот элемент. Этот случай, который мы условно назвали “горячим резервированием”, самый простой их всех возможных. Гораздо сложнее случай, когда резервный элемент до своего включения в работу вообще не может отказывать (“холодное” резервирование) или может отказывать, но с другой, меньшей плотностью вероятности, чем после включения (“облегченное” резервирование).
При рассмотрении задач, связанных с холодным или облегченным резервированием, нам недостаточно будет вводить надежности системы и элементов, заранее фиксированного, значения времени t; необходимо будет проанализировать весь случайный процесс функционирования системы.
Контрольные вопросы:
Что подразумевают под понятием "горячий резерв"?
Чему равна надежность системы с "параллельным соединением"?
Л.: [7] С. 27-28; [9] С. 24-27; [11] С. 26-29; [14] С. 21-23.
Лекция 7. Надежность системы управления и его элементов с восстановлением
План лекций
Надежность резервированной системы
Общая интенсивность отказов при резервированной системы
Определение количественные характеристики надежности резервированной системы
До сих пор, рассматривая задачи надежности, мы исходили из того, что отказавший элемент выходит из строя окончательно и, никакого восстановления его функций не производится. Представляет интерес исследование задач надежности, где отказавшие элементы восстанавливаются, т.е. мгновенно заменяются новыми или ремонтируются.
При решении такого рода задач мы будем предполагать, что все потоки событии, переводящие систему из состояния в состояние.
Предварительно сделаем следующее замечание:
все процессы, связанные с надежностью систем, которые мы рассматривали до сих пор, были существенно нестационарными;
так как восстановления элементов не было, естественно, что при  надежность системы стремилась к нулю, и "предельным режимом" системы просто было <<не работает>>. надежность системы стремилась к нулю, и "предельным режимом" системы просто было <<не работает>>.
В задачах с восстановлением нас будут интересовать не только переходные процессы в системе, но и установившиеся режимы. В данном параграфе мы рассмотрим несколько задач из области надежности систем с восстановлением.
Задача 7л.1.
(задача о запасных элементах). Работает простая система, состоящая из одного элемента Э, который подвергается простейшему потоку отказов с интенсивностью 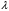 . При отказе элемент мгновенно заменяется новым с таким же характеристиками. В нашем распоряжении имеется N запасных элементов, находящихся в <<холодном>> резерве. Определить вероятность того, что этого числа запасных элементов нам хватит для обеспечения работы системы в течение времени (другими словами, найти надежность P(t) системы с восстановлением). . При отказе элемент мгновенно заменяется новым с таким же характеристиками. В нашем распоряжении имеется N запасных элементов, находящихся в <<холодном>> резерве. Определить вероятность того, что этого числа запасных элементов нам хватит для обеспечения работы системы в течение времени (другими словами, найти надежность P(t) системы с восстановлением).
Решение.
Нетрудно заметить, что поставленная задача эквивалентна задаче оценки надежности резервированной системы с Nрезервными элементами, работающими в холодном резерве и, как таковая, может быть решена методами, предложенными выше. Но мы решим ее несколько иным, более простым методом.
Рассмотрим на оси 0t <поток восстановления>, т.д. последовательность моментов времени, в которые выходят из строя и мгновенно восстанавливаются элементы. Очевидно это - простейший поток с интенсивностью 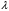 . Надежность системы P(t) есть вероятность того, что к моменту t система будет работать. Для этого нужно, чтобы на участке (0,t) отказало не более N элементов (один основной и N-1 запасных). . Надежность системы P(t) есть вероятность того, что к моменту t система будет работать. Для этого нужно, чтобы на участке (0,t) отказало не более N элементов (один основной и N-1 запасных).
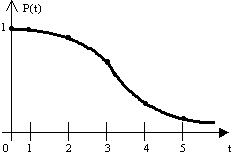
Рисунок 6л.1 - График работы элемента с восстановлением
Мы знаем, что число событий простейшего потока, попадающих на участок длиной t, распределено по закону Пуассона:
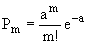 (6л.1) (6л.1)
где a= 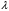 t, т.е. t, т.е.
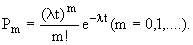 (6л.2) (6л.2)
Найдем вероятность того, что число точек (событий), попадающих на участок (0,t), будет не больше N. Эта вероятность и будет надежностью системы
 (6л.3) (6л.3)
или, короче,
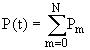 (6л.4) (6л.4)
Подставляя (6л.2) в (6л.3), получим:
 (6л.5) (6л.5)
или, вынося за знак суммы,
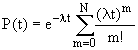 (6л.6) (6л.6)
Вычисления по формулам (6л.5) или (6л.6) удобно производить, пользуясь таблицами пуассоновского распределения P (или вероятностей R ,которые несколько удобнее табулируются).
Рассмотренные задачи и примеры показывают, что математический аппарат, применяемый для анализа надежности технических устройств, в сущности, совпадает с аппаратом теории массового обслуживания, и исследование процессов, протекающих в системах с ненадежными элементами, при известных условиях может быть проведено методами теории непрерывных Марковских цепей. Для этого нужно, чтобы потоки событий, переводящие элементы из состояния в состояние, были (точно или приближенно) пуассоновскими. Эти потоки необязательно должны быть стационарными, но, во всяком случае, такими, чтобы интенсивности потоков событий не зависели от случайных моментов переходов системы из состояния в состояние. Для наиболее простого, стационарного случая это означает, что, в частности, все законы надежности должны быть экспоненциальными, а законы распределения времени восстановления - тоже показательными или близким к показательным.
Контрольные вопросы:
Что такое восстановление системы?
Как рассчитывается вероятность работы системы с восстановлением?
По какой формуле можно найти, сколько запасных элементов необходимо системе для достижения определенной надежности?
Чем отличается задержанное восстановление от обычного восстановления?
Как вычисляется надежность системы из нескольких элементов с задержанным восстановлением?
Л.: [2] С. 25-28; [4] С. 24-27; [5] С. 26-29; [6] С. 31-33.
Лекция 8. Определение количественных характеристик надежности по статистическим данным об отказах системы управления
План лекций
Вероятность безотказной работы по статистическим данным
Частота отказов по статистическим данным
Интенсивность отказов по статистическим данным
Среднее время безотказной работы
Дисперсия времени безотказной работы
Вероятность безотказной работы по статистическим данным об отказах оценивается выражением
|
 Скачать 388.57 Kb.
Скачать 388.57 Kb.