Рисунок 2л.1 - График плотности f(t)
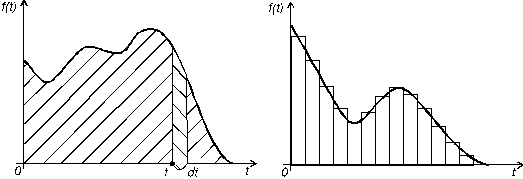
Рисунок 2л.2 - Гистограмма плотности f(t)
График плотности f(t) показан на рисунке 2л.1. Площадь, ограниченная кривой f(t), равна единице.
Величина f(t)dt - элемент вероятности - истолковывается как вероятность того, что время T примет значение, лежащее в пределах элементарного участка (t, t+dt).
В литературе надежность функции f(t) часто называют "плотностью отказов". Во избежание недоразумений, связанных с нечеткой терминологией, мы будем называть f(t) более точно: плотностью распределения времени безотказной работы.
Плотность f(t) может быть приближенно определена из опыта, для чего ставиться следующий эксперимент: наблюдается работа большого числа N однородных элементов; каждый из них работает до момента отказа. Время, в течение которого работал элемент, регистрируется. Полученные значения времени:
t1, t2, …., tN (2л.2)
обрабатываются обычными методами математической статистики: строиться гистограмма (рисунок 2л.2) и выравнивается с помощью какой-нибудь плавной кривой, обладающей свойствами плотности.
Ордината гистограммы на каждом элементарном участке времени 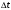 представляет собой не что иное, как среднее число отказов за единицу времени, приходящееся на один испытанный элемент. Тот же смысл можно приписать и функции f(t). Приближенно плотность f(t) определяется по формуле представляет собой не что иное, как среднее число отказов за единицу времени, приходящееся на один испытанный элемент. Тот же смысл можно приписать и функции f(t). Приближенно плотность f(t) определяется по формуле
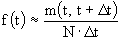 (2л.3) (2л.3)
где m(t, t+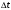 ) - число элементов, оказавших на участке времени от t до t+ ) - число элементов, оказавших на участке времени от t до t+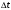 (время отсчитывается от момента включение); N - длина элементарного участка времени. (время отсчитывается от момента включение); N - длина элементарного участка времени.
Контрольные вопросы:
Укажите зависимость ненадежности элемента от его надежности?
Чем является функция распределения безотказной работы?
Что такое плотность распределения времени безотказной работы?
Объясните геометрический смысл среднего времени безотказной работы?
Л.: [6] С. 7-11; [7] С. 14-17; [8] С. 16-19; [9] С. 6-10.
Лекция 3. Биномиальное распределение
План лекций
Биномиальное закон распределение
Расчет вероятность 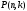 при помощи биномиального закона при помощи биномиального закона
Пусть некоторый опыт повторяется  раз и отдельные опыты этой серии не зависят друг от друга. Пусть в каждом опыте может произойти или не произойти событие раз и отдельные опыты этой серии не зависят друг от друга. Пусть в каждом опыте может произойти или не произойти событие 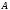 , а вероятность его осуществления в отдельном опыте не зависит от номера опыта и равна , а вероятность его осуществления в отдельном опыте не зависит от номера опыта и равна 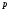 . Пусть . Пусть 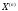 - число наступлений события - число наступлений события 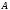 в такой серии из в такой серии из  опытов. Очевидно, что возможные значения случайной величины опытов. Очевидно, что возможные значения случайной величины 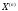 суть числа суть числа 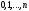 . Вероятности . Вероятности 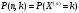 , ,
вычисляются по биномиальному закону:
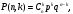  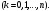 (3л.1) (3л.1)
Случайная величина называется биномиально распределенной с параметрами  и и 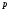 , если возможные значения , если возможные значения 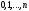 она принимает с вероятностями она принимает с вероятностями 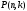 ,задаваемыми формулой (3л.1). Параметры ,задаваемыми формулой (3л.1). Параметры  и и 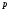 полностью определяют биномиальное распределение. На рисунке 3л.1 полностью определяют биномиальное распределение. На рисунке 3л.1
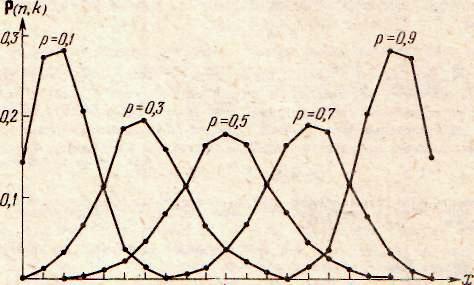
0 2 4 6 8 10 12 14 16 18 20
Рисунок 3л.1 - Полигоны биномиальных распределений
показаны: «полигоны» биномиальных распределений для 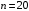 и различных и различных 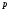 . При этом соответствующие . При этом соответствующие 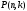 отложены по ординате и соединены ломаной линией. отложены по ординате и соединены ломаной линией.
Начиная с 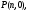 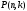 могут быть легко вычислены по следующей рекуррентной формуле: могут быть легко вычислены по следующей рекуррентной формуле:
 (3л.2) (3л.2)
Контрольные вопросы:
Что такое биномиальное закон распределение?
Как вычисляется вероятность  при помощи биномиального закона? при помощи биномиального закона?
Л.: [2] С. 8-11; [3] С. 14-15; [5] С. 16-17;
Лекция 4. Экспоненциальный закон надежности
План лекций
Экспоненциальный (или показательный) закон надежности
Вероятность безотказной работы резервированной системы
Среднее время безотказной работы резервированной системы
Наиболее удобным для аналитического описания является так называемый экспоненциальный (или показательный) закон надежности, который выражается формулой
р(t)=е-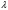 t, (4л.1) t, (4л.1)
где 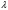 >0 - постоянный параметр. >0 - постоянный параметр.

|
 Скачать 388.57 Kb.
Скачать 388.57 Kb.