Для тестов. I. Глоссарий
 Скачать 388.57 Kb. Скачать 388.57 Kb.
|
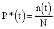 , (8л.1) , (8л.1)где n(t) - число изделий, не отказавших к моменту времени t; N- число изделий, поставленных на испытания; Р*(t) - статистическая оценка вероятности безотказной работы изделия. Для вероятности отказа по статистическим данным справедливо соотношение 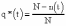 , (8л.2) , (8л.2)где N-n(t) - число изделий, отказавших к моменту времени t; q*(t) - статистическая оценка вероятности отказа изделия. Частота отказов по статистическим данным об отказах определяется выражением 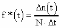 , (8л.3) , (8л.3)где n(t) - число отказавших изделий на участке времени (t, t+ 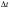 ); f*(t) - статистическая оценка частоты отказов изделия; ); f*(t) - статистическая оценка частоты отказов изделия; 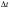 - интервал времени. - интервал времени. Интенсивность отказов по статистическим данным об отказах определяется формулой 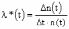 , (8л.4) , (8л.4)где n(t) - число изделий, не отказавших к моменту времени t; 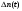 - число отказавших изделий на участке времени (t, t+ - число отказавших изделий на участке времени (t, t+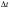 ); ); 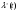 - статистическая оценка интенсивности отказов изделия. - статистическая оценка интенсивности отказов изделия. Среднее время безотказной работы изделия по статистическим данным оценивается выражением  , (8л.5) , (8л.5)где ti - время безотказной работы i-го изделия; N- общее число изделий, поставленных на испытания; mt* - статистическая оценка среднего времени безотказной работы изделия. Для определения mt* по формуле (8л.5) необходимо знать моменты выхода из строя всех N изделий. Можно определять mt* из уравнения 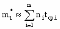 , (8л.6) , (8л.6)где ni - количество вышедших из строя изделий в i-ом интервале времени; tср.i = (ti-1+ti)/2; m=tk/t; t=ti+1-ti; ti-1 -время начала i-го интервала; ti - время конца i-го интервала; tk - время, в течение которого вышли из строя все изделия;  - интервал времени. - интервал времени. Дисперсия времени безотказной работы изделия по статистическим данным определяется формулой 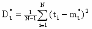 , (8л.7) , (8л.7)где Dt*- статистическая оценка дисперсии времени безотказной работы изделия. Контрольные вопросы: Что такое вероятность безотказной работы по статистическим данным? Что такое частота отказов по статистическим данным? Что такое интенсивность отказов по статистическим данным? Что такое среднее время безотказной работы? Что такое дисперсия времени безотказной работы? Л.: [1] С. 29-30; [3] С. 28-29; [7] С. 29-31; [9] С. 32-33. Лекция 9. Аналитическое определение количественных характеристик надёжности системы управления План лекций Определение количественные характеристики надежности Параметры экспоненциального закона распределения времени безотказной работы Параметры нормального закона распределения времени безотказной работы Параметры закона распределения Вейбулла времени безотказной работы Параметры закона распределения Релея времени безотказной работы Формулы, по которым определяются количественные характеристики надежности изделия 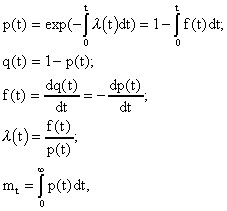 (9л.1) (9л.2) (9л.3) (9л.4) (9л.5) где p(t) - вероятность безотказной работы изделия на интервале времени от 0 до t; q(t) - вероятность отказа изделия на интервале времени от 0 до t; f(t) - частота отказов изделия или плотность вероятности времени безотказной работы изделия Т; 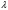 (t) - интенсивность отказов изделия; (t) - интенсивность отказов изделия; mt - среднее время безотказной работы изделия. Формулы (9л.1) - (9л.5) для экспоненциального закона распределения времени безотказной работы изделия примут вид 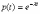 ; (9л.6) ; (9л.6) 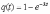 ; (9л.7) ; (9л.7) 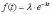 ; (9л.8) ; (9л.8) 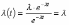 ; (9л.9) ; (9л.9) 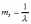 . (9л.10) . (9л.10)Формулы (9л.1) - (9л.5) для нормального закона распределения времени безотказной работы изделия примут вид  (9л.11) (9л.11)где 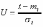 ; ;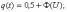 (9л.12) (9л.12)где 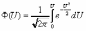 ; ;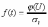 ; (9л.13) ; (9л.13)где 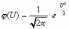 ; ;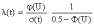 , (9л.14) , (9л.14) где Ф(U) - функция Лапласа, обладающая свойствами Ф(0) = 0; (9л. 15) Ф(-U) = -Ф(U); (9л.16) Ф(U) = 0.5. (9л.17) Здесь mt - среднее значение случайной величины Т; 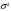 - дисперсия случайной величины Т; Т- время безотказной работы изделия. - дисперсия случайной величины Т; Т- время безотказной работы изделия. Формуды (9л.1) - (9л.5) для закона распределения Вейбулла времени безотказной работы изделия имеют вид  ; (9л.18) ; (9л.18)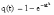 ; (9л.19) ; (9л.19)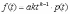 ; (9л.20) ; (9л.20)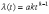 ; (9л.21) ; (9л.21)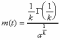 , (9л.22) , (9л.22)где a, k - параметры закона распределения Вейбулла. Г(x) - гамма-функция. Формулы (9л.1) - (9л.5) для закона распределения Релея времени безотказной работы изделия имеют вид 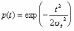 ; ; 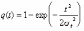 ; (9л.23) ; (9л.23)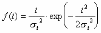 ; ;  ; (9л.24) ; (9л.24)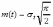 ; (9л.25) ; (9л.25)где mt - мода распределения случайной величины Т; Т - время безотказной работы изделия. Контрольные вопросы: Как определить количественные характеристики надежности? Как рассчитывается, параметры экспоненциального закона распределения времени безотказной работы? Как рассчитывается, параметры нормального закона распределения времени безотказной работы? Как рассчитывается, параметры закона распределения Вейбулла времени безотказной работы? Как рассчитывается, параметры закона распределения Релея времени безотказной работы?Л.: [5] С. 27-29; [6] С. 29-31; [7] С. 31-32; [9] С. 33-34. Лекция 10. Последовательное соединение элементов системы управления План лекций Система последовательно соединенных элементов Вероятность безотказной работы системы Частота отказов системы Интенсивность отказов системы Среднее время безотказной работы системы Соединение элементов называется последовательным, если отказ хотя бы одного элемента приводит к отказу всей системы. Система последовательно соединенных элементов работоспособна тогда, когда работоспособны все ее элементы. Вероятность безотказной работы системы за время t определяется формулой Pc(t) =P1(t)*P2(t)...Pn(t)= 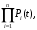 (10л.1) (10л.1) где Рi(t) - вероятность безотказной работы i-го элемента за время t. Если Рi(t) =Р(t), то Pc(t)=Pn(t). (10л.2) Выразим Рс(t) через интенсивность отказов 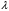 i(t) элементов системы. i(t) элементов системы. Имеем: 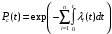 (10л. 3) (10л. 3)или 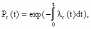 (10л.4) (10л.4)где  (10л.5) (10л.5) Здесь 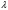 i(t) - интенсивность отказов i-го элемента; i(t) - интенсивность отказов i-го элемента; 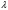 с(t) - интенсивность отказов системы. с(t) - интенсивность отказов системы. Вероятность отказа системы на интервале времени (0, t ) равна 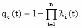 (10л.6) (10л.6) Частота отказов системы fc(t): 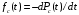 (10л.7) (10л.7)Интенсивность отказов системы: 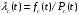 (10л.8) (10л.8)Среднее время безотказной работы системы: 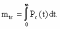 (10л. 9) (10л. 9)В случае экспоненциального закона надежности всех элементов системы имеем 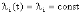 . . 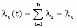 (10л.10) (10л.10)  ; ; 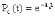 (10л.11) (10л.11)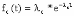 ; ; 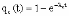 (10л.12) (10л.12) 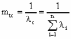 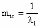 (10л.13) (10л.13) где mti - среднее время безотказной работы i - го элемента. При расчете надежности систем часто приходится перемножать вероятности безотказной работы отдельных элементов расчета, возводить их в степень и извлекать корни. При значениях Р(t), близких к единице, эти вычисления можно с достаточной для практики точностью выполнять по следующим приближенным формулам: 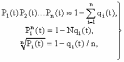 (10л.14) (10л.14) где qi(t) - вероятность отказа i - го элемента. Контрольные вопросы: Как вычисляется надежность системы последовательно соединенных элементов? Как вычисляется вероятность безотказной работы системы? Как вычисляется частота отказов системы? Как вычисляется интенсивность отказов системы? Как вычисляется среднее время безотказной работы системы? Л.: [5] С. 29-31; [6] С. 28-30; [7] С. 32-33; [9] С. 34-35. Лекция 11. Расчет надежности системы управления с постоянным резервированием План лекций Постоянное резервирование резервные элементы системы Определение количественные характеристики надежности системы с общим резервированием При постоянном резервировании резервные элементы 1,2,.... соединены параллельно с основным (рабочим) элементом в течение всего периода работы системы. Все элементы соединены постоянно, перестройка схемы при отказах не происходит, отказавший элемент не отключается. Вероятность отказа системы qc(t) определяется формулой 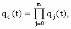 (11л.1) (11л.1) где qj(t) - вероятность отказа j - го элемента. Вероятность безотказной работы системы 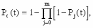 (11л.2) (11л.2) где Рj(t) - вероятность безотказной работы j - го элемента. Если Рj(t) =Р(t), j = 0, 1, . . . , m, то 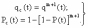 (11л.3) (11л.3)При экспоненциальном законе надежности отдельных элементов имеем 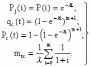 (11л.4) (11л.4)Резервирование называется общим, если резервируется вся система, состоящая из последовательного соединения n элементов. Основная цепь содержит n элементов. Число резервных цепей равно m, т. е. кратность резервирования равна m. Определим количественные характеристики надежности системы с общим резервированием (резервные цепи включены постоянно). Запишем вероятность безотказной работы j - ой цепи 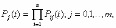 (11л.5) (11л.5) где Рij(t), j=0,1,2,...m; i=1,2,3,...,n - вероятность безотказной работы элемента Эij. Вероятность отказа j - ой цепи 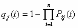 . (11л.6) . (11л.6) Вероятность отказа системы с общим резервированием 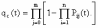 . (11л.7) . (11л.7)Вероятность безотказной работы системы с общим резервированием 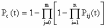 . (11л.8) . (11л.8) Частный случай: основная и резервные цепи имеют одинаковую надежность, т.е. Рij(t)=Pi(t). (11л.9) Тогда 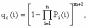 (11л.10) (11л.10)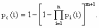 (11л.11) (11л.11)Рассмотрим экспоненциальный закон надежности, т. е. Pi(t)=e-  t . (11л.12) t . (11л.12)В этом случае формулы (11л.10), (11л.11) примут вид qc(t)=(1-e-0t)m+1, (11л.13) Pc(t)=1-(1-e-0t)m+1, (11л.14)  , (11л.15) , (11л.15)где 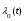 - интенсивность отказов цепи, состоящей из n элементов. - интенсивность отказов цепи, состоящей из n элементов. Частота отказов системы с о6щим резервированием  . (11л.16) . (11л.16) Интенсивность отказов системы с общим резервированием 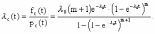 (11л.17) (11л.17)Среднее время безотказной работы резервированной системы 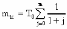 , (11л.18) , (11л.18) где Т0 = 1/ 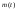 0 - среднее время безотказной работы нерезервированной системы. 0 - среднее время безотказной работы нерезервированной системы. Контрольные вопросы: Как проводится постоянное резервирование резервные элементы системы? Как определить количественные характеристики надежности системы с общим резервированием? Л.: [5] С. 30-32; [6] С. 31-33; [7] С. 34-35; [9] С. 36-37. Лекция 12. Расчет надежности системы управления с поэлементным резервированием План лекций Поэлементное резервирование элементы системы Определение количественные характеристики надежности системы при поэлементное резервирование элементы системы При поэлементном резервировании резервируются отдельно элементы системы. Определим количественные характеристики надежности системы. Запишем вероятность отказа i -ой группы. Имеем 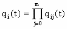 ; ; 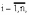 (12л.1) (12л.1) где qij(t) - вероятность отказа элемента Эijна интервале времени (0, t). Запишем вероятность безотказной работы j-ой группы. Получим 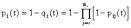 ; ;  , (12л.2) , (12л.2) где Pij(t) - вероятность безотказной работы элемента Э |
