Методичка жбк. Методичка ЖБК. I. Проектирование бетонной подпорной стенки
 Скачать 290.42 Kb. Скачать 290.42 Kb.
|
|
IV. Расчет и конструирование ригеля Р-1 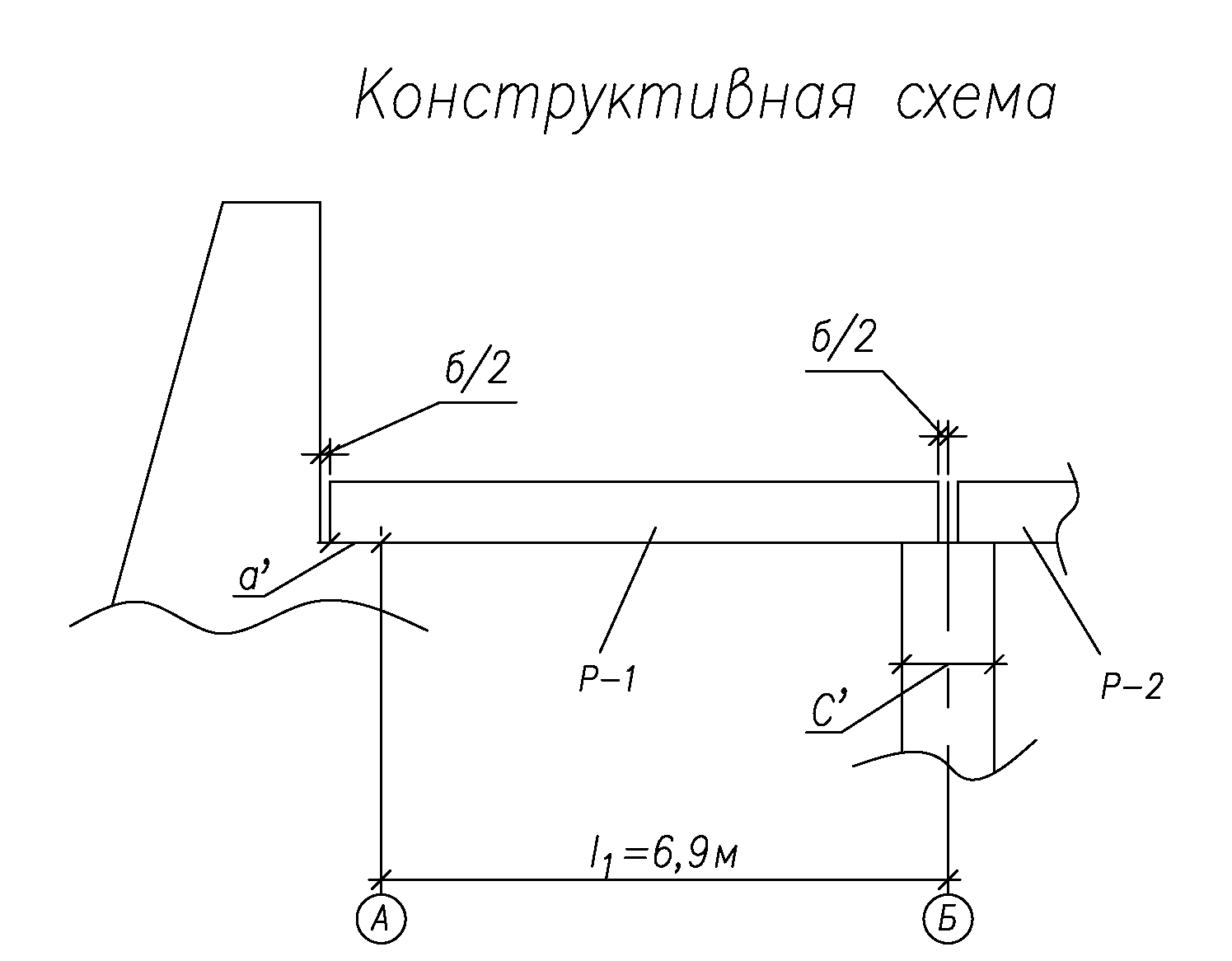 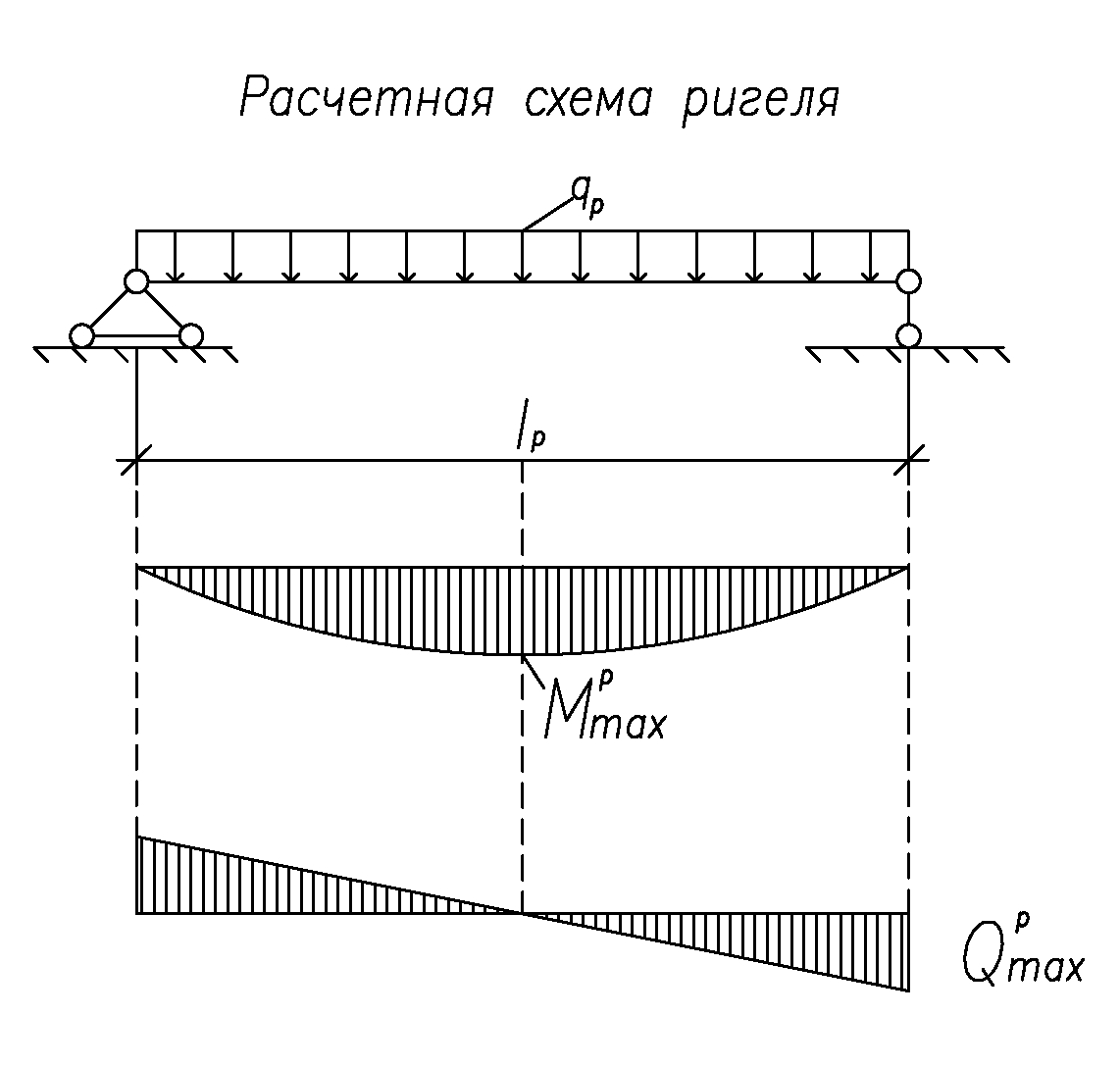 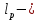 расчетная длина ригеля: расчетная длина ригеля: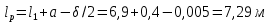 , где: 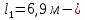 заданный пролет ригеля в осях; заданный пролет ригеля в осях;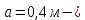 длина операния ригеля на уступ; длина операния ригеля на уступ;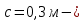 ширина сваи; ширина сваи;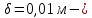 щель для забивания свай. щель для забивания свай.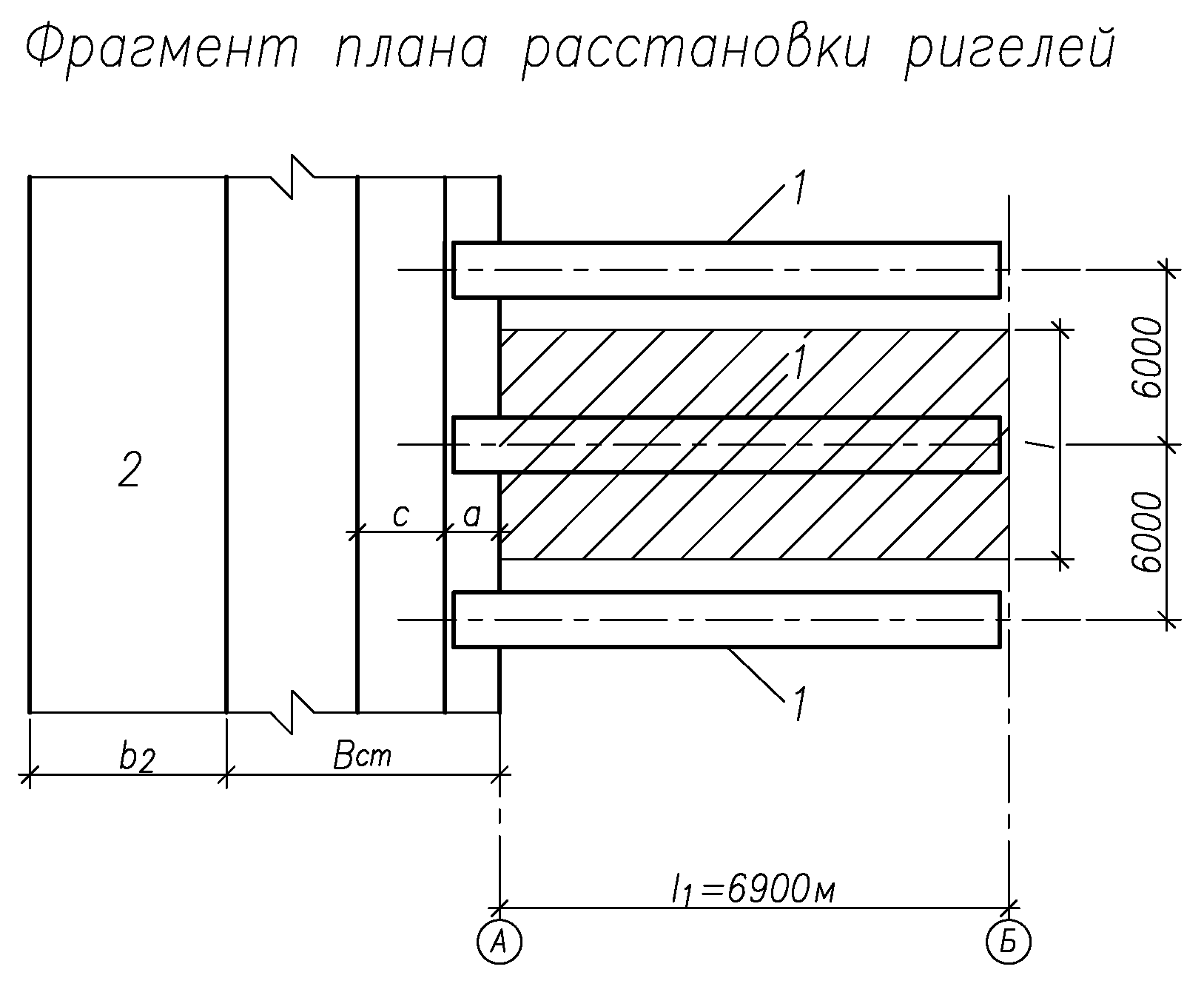 1     - ригели; 2- подпорная стенка; - грузовая площадка для ригеля. - ригели; 2- подпорная стенка; - грузовая площадка для ригеля.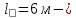 ширина грузовой площадки. ширина грузовой площадки.4.1 Расчетная нагрузка на ригель 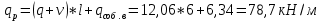 где: 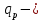 расчетная нагрузка на ригель; расчетная нагрузка на ригель;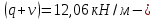 суммарная расчетная нагрузка, действующая на плиту перекрытия; суммарная расчетная нагрузка, действующая на плиту перекрытия;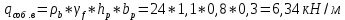 где: 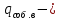 собственный вес ригеля; собственный вес ригеля;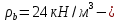 плотность бетона; плотность бетона;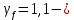 коэффициент надежности по нагрузке; коэффициент надежности по нагрузке; предварительно задаемся 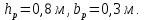 7 7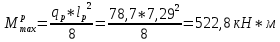 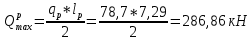 Требуемая по расчету рабочая высота сечения ригеля 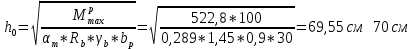 Задаемся классов бетона В25: Начальный модуль упругости: 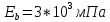 Расчетные сопротивления: 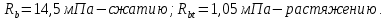 Рабочая арматура А400: 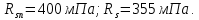 Задаемся относительной величиной сжатой зоны бетона: 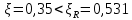 По приложению 10 находим 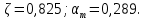 Следовательно, 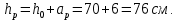 Собственный вес ригеля не пересчитываем, так как в запас прочности получается больший вес. Находим истинное значение коэффициента 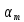 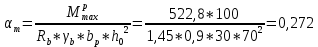 По приложению 10 находим 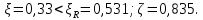 Определение требуемой площади сечения рабочей арматуры 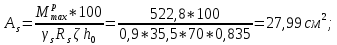 По сортаменту принимаем 4 шт диаметром 32 с 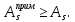 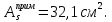 4.2 Расчет ригеля на действие поперечной силы по наклонному сечению. Условие прочности расчета на поперечную силу 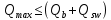 , где : 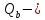 поперечная сила воспринимаемая бетоном, которую определяют по двум эмпирическим формулам СНиПа : поперечная сила воспринимаемая бетоном, которую определяют по двум эмпирическим формулам СНиПа : 1) 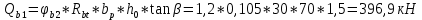 , где : 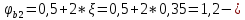 коэффициент условия работы бетона коэффициент условия работы бетона 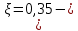 относительная высота сжатой зоны бетона относительная высота сжатой зоны бетона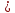 ; ;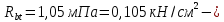 расчетное сопротивление бетона растяжению; расчетное сопротивление бетона растяжению;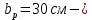 ширина сжатой границы ригеля; ширина сжатой границы ригеля;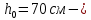 рабочая высота плиты; рабочая высота плиты;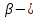 угол наибольшего откоса трещин, угол наибольшего откоса трещин, 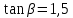 . .2) 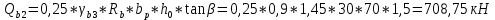 , где: 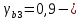 коэффициент условия работы; коэффициент условия работы; 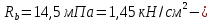 расчетное сопротивление бетона растяжению. Принимаем меньшее из значений: расчетное сопротивление бетона растяжению. Принимаем меньшее из значений: 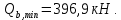 Поперечная сила, воспринимаемая поперечной арматурой: 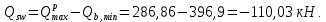 Так как поперечная сила получилась отрицательной, следовательно, всю действующую поперечную силу воспринимает бетон, значит, поперечную арматура ставим конструктивно: 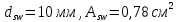 . . 4.3 Расчет ригеля по II предельному состоянию по деформациям 4.3.1. Расчет на трещинообразование Определение максимального изгибающего момента, действующего от нормативных нагрузок 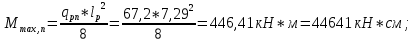 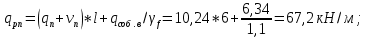 где: 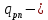 нормативная равномерная распределенная нагрузка на ригель. нормативная равномерная распределенная нагрузка на ригель.Следует сравнить этот момент с моментом, при котором образуются трещины (момент трещинообразования). 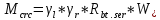 , где: 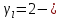 при расположении рабочей продольной арматуры в один ряд; при расположении рабочей продольной арматуры в один ряд;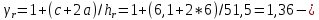 эмпирический коэффициент; эмпирический коэффициент;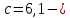 для бетона класса В25; для бетона класса В25;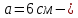 расстояние от нижней грани до рабочей арматуры; расстояние от нижней грани до рабочей арматуры;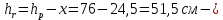 высота растянутой зоны бетона; высота растянутой зоны бетона;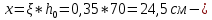 высота сжатой зоны бетона; высота сжатой зоны бетона;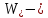 момент сопротивления приведенного сечения ригеля, т.е. следует привести площадь сечения арматуры к сечению бетона. момент сопротивления приведенного сечения ригеля, т.е. следует привести площадь сечения арматуры к сечению бетона. Определение момента сопротивления приведенного сечения 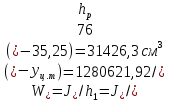 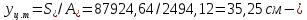 положение центра тяжести положение центра тяжести 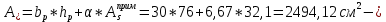 площадь приведенного сечения; площадь приведенного сечения;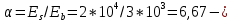 коэффициент приведения; коэффициент приведения;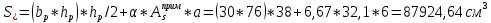 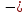 статический момент приведенного сечения; статический момент приведенного сечения;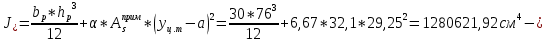 момент инерции приведенного сечения относительно нейтральной оси. 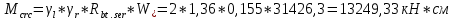 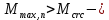 следовательно, трещины образуются. следовательно, трещины образуются. 4.3.2 Расчет на раскрытие трещин Принимаем, что причальная площадка относиться к 3 категории зданий по трещиностойкости, то есть предельно допустимая ширина раскрытия трещин при продолжительном раскрытии 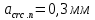 , а при не продолжительном раскрытии , а при не продолжительном раскрытии 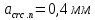 . .Ширина раскрытия трещин определяется по формуле: а) При непродолжительном раскрытии трещин: 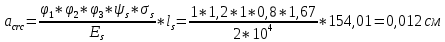 , где: 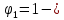 коэффициент учитывающий продолжительность действия нагрузки; коэффициент учитывающий продолжительность действия нагрузки;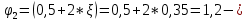 коэффициент, учитывающий профиль продольной арматуры. коэффициент, учитывающий профиль продольной арматуры. 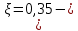 относительная высота сжатой зоны бетона относительная высота сжатой зоны бетона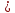 ; ;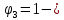 коэффициент, учитывающий характер загруженности; коэффициент, учитывающий характер загруженности;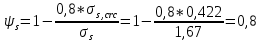 , где: 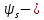 коэффициент учитывающий неравномерность относительных деформаций растянутой арматуры между трещинами; коэффициент учитывающий неравномерность относительных деформаций растянутой арматуры между трещинами;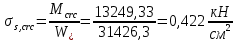 , где: 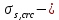 напряжение в растянутой продольной арматуре в момент образования трещин; напряжение в растянутой продольной арматуре в момент образования трещин;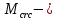 момент образования трещин; момент образования трещин;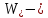 момент сопротивления приведенного сечения; момент сопротивления приведенного сечения;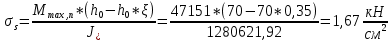 , где: 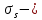 напряжение в продольной рабочей арматуре до образования трещин; напряжение в продольной рабочей арматуре до образования трещин;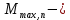 максимальный изгибающий момент от нормативных нагрузок; максимальный изгибающий момент от нормативных нагрузок;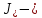 момент инерции приведенного сечения относительно нейтральной оси; момент инерции приведенного сечения относительно нейтральной оси;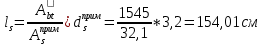 , где: 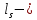 расстояние между вершинами трещин; расстояние между вершинами трещин;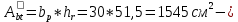 площадь сечения растянутой зоны; площадь сечения растянутой зоны;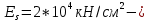 модуль упругости стали. модуль упругости стали.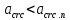 ; ; 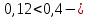 условие выполняется. условие выполняется. а) При продолжительном раскрытии трещин : 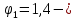 коэффициент, учитывающий продолжительность действия нагрузки. коэффициент, учитывающий продолжительность действия нагрузки.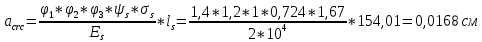 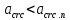 ; ; 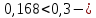 условие выполняется. условие выполняется. Если условие не выполняется, то это значит, что плита не выдерживает нагрузку и нужно увеличить высоту сечения плиты. 4.3.3. Расчет ригеля на прогиб Предельно допустимая величина прогиба: 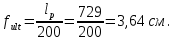 Максимальная величина прогиба для шарнирно опертого изгибаемого элемента: 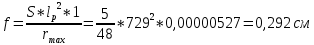 , где: 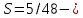 при шарнирном оперании; при шарнирном оперании;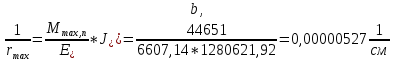 , где: 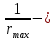 максимальная кривизна; максимальная кривизна;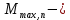 максимальный изгибающий момент от нормативных нагрузок; максимальный изгибающий момент от нормативных нагрузок;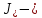 момент инерции приведенного сечения относительно нейтральной оси; момент инерции приведенного сечения относительно нейтральной оси;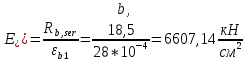 , где: 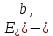 приведенный модуль упругости; приведенный модуль упругости;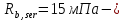 расчетное сопротивление бетона сжатию по второму предельному состоянию; расчетное сопротивление бетона сжатию по второму предельному состоянию;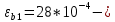 относительная деформация бетона при сжатии. относительная деформация бетона при сжатии.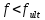 ; ; 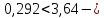 условие выполняется. условие выполняется. 4.4 Расчет арматуры в ригеле Проектируем ригель с поперечным сечением таврового вида с полкой в низу, так как так удобнее расположить плиты перекрытия площадки.  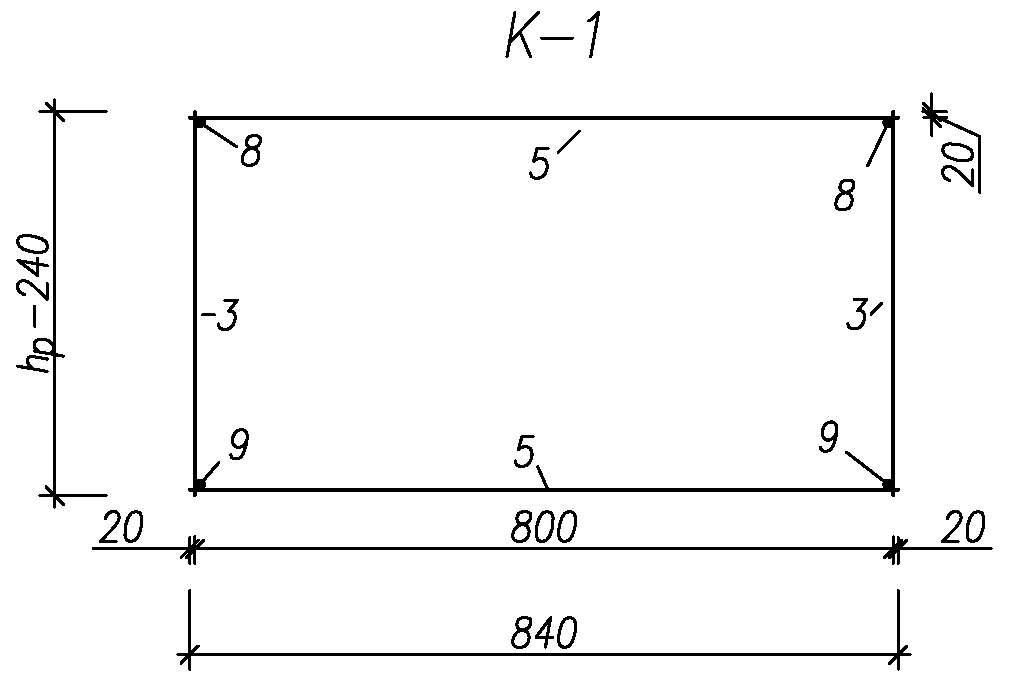 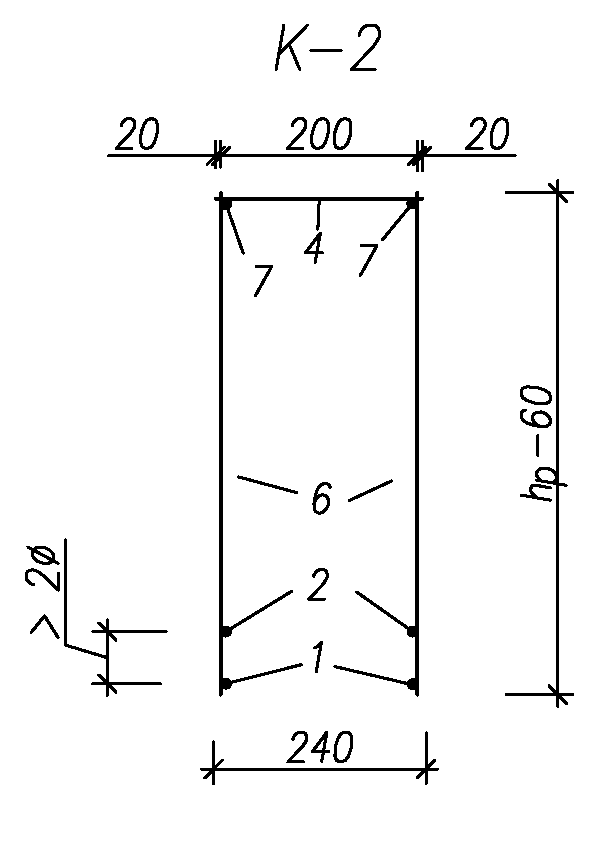 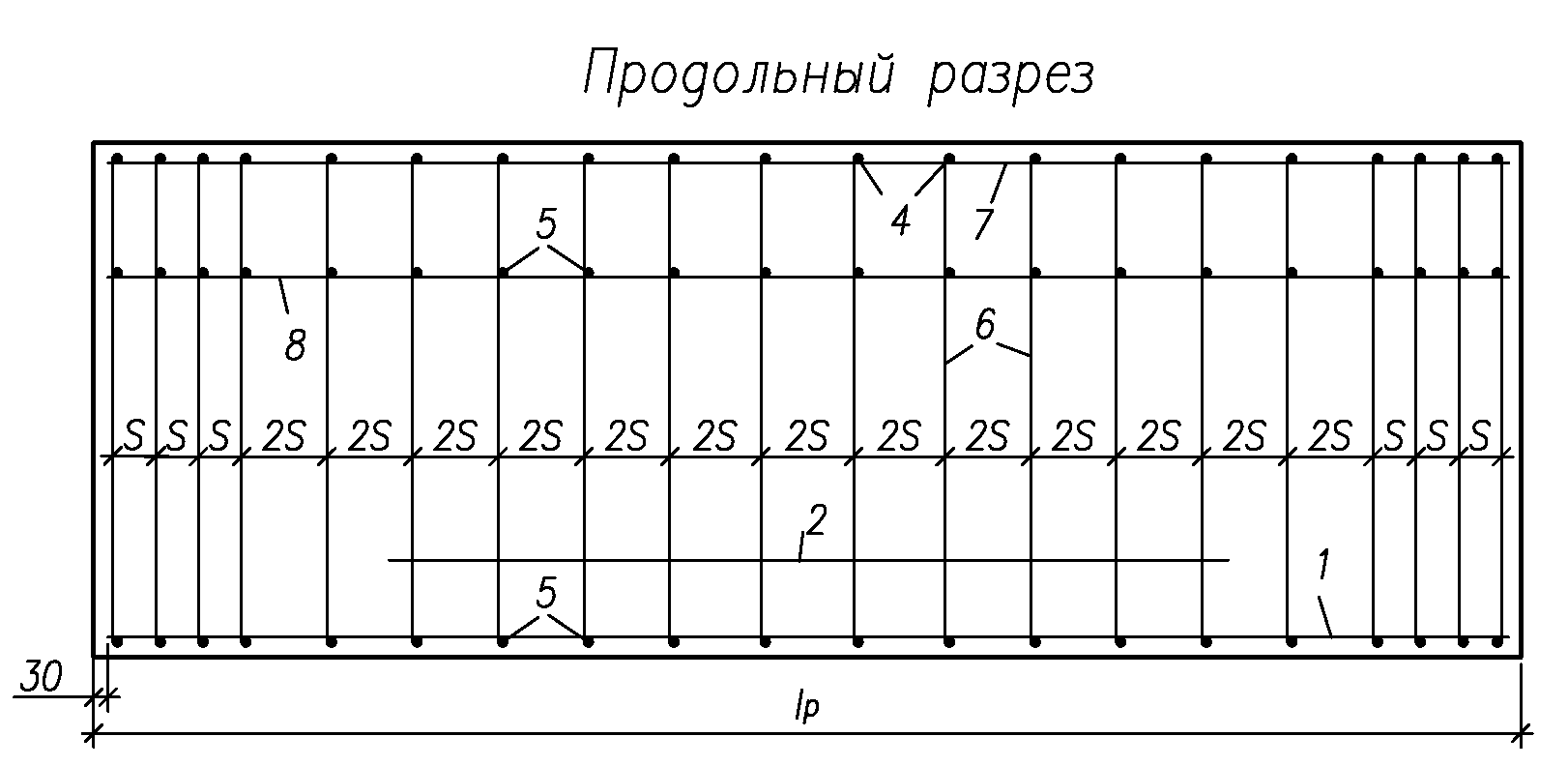 1,2- продольная рабочая арматура (расчетная); 6-попереяная арматура; 3,4,5,7,8- монтажная арматура для объединения всей арматуры в каркасы К-1 и К-2. Так как продольная рабочая арматура расположена по максимально изгибающему моменту, а на опорах моменты равны 0, то экономически не целесообразно принимать это сечение арматуры по всей длине ригеля. По этому обрываем 1 ряд арматуры (верхний) с обеих сторон. Необходимо определить положение точек обрыва. Для этого строится эпюра материалов.  1) Определяем изгибающий момент воспринимаемый поперечным сечением ригеля с одним рядом рабочей продольной арматуры (2 диаметра 32 мм). 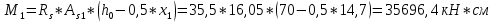 , где 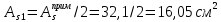 ; ;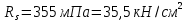 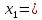 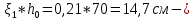 высота сжатой зоны бетона; высота сжатой зоны бетона;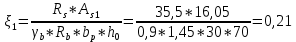 Откладываем полученный момент на эпюре моментов от внешней нагрузки, из полученной точки проводим горизонтальные линии до пересечения с эпюрой моментов от внешней нагрузки. И получаем точки теоретического обрыва арматуры. 2) Определяем изгибающий момент, воспринимаемый поперечным сечением ригеля с двумя рядами рабочей продольной арматуры (4 диаметра 32 мм). 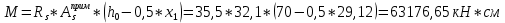 , где 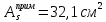 ; ;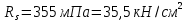 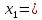 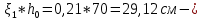 высота сжатой зоны бетона; высота сжатой зоны бетона;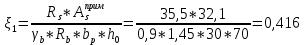 Откладываем полученный момент на эпюре моментов от внешней нагрузки. 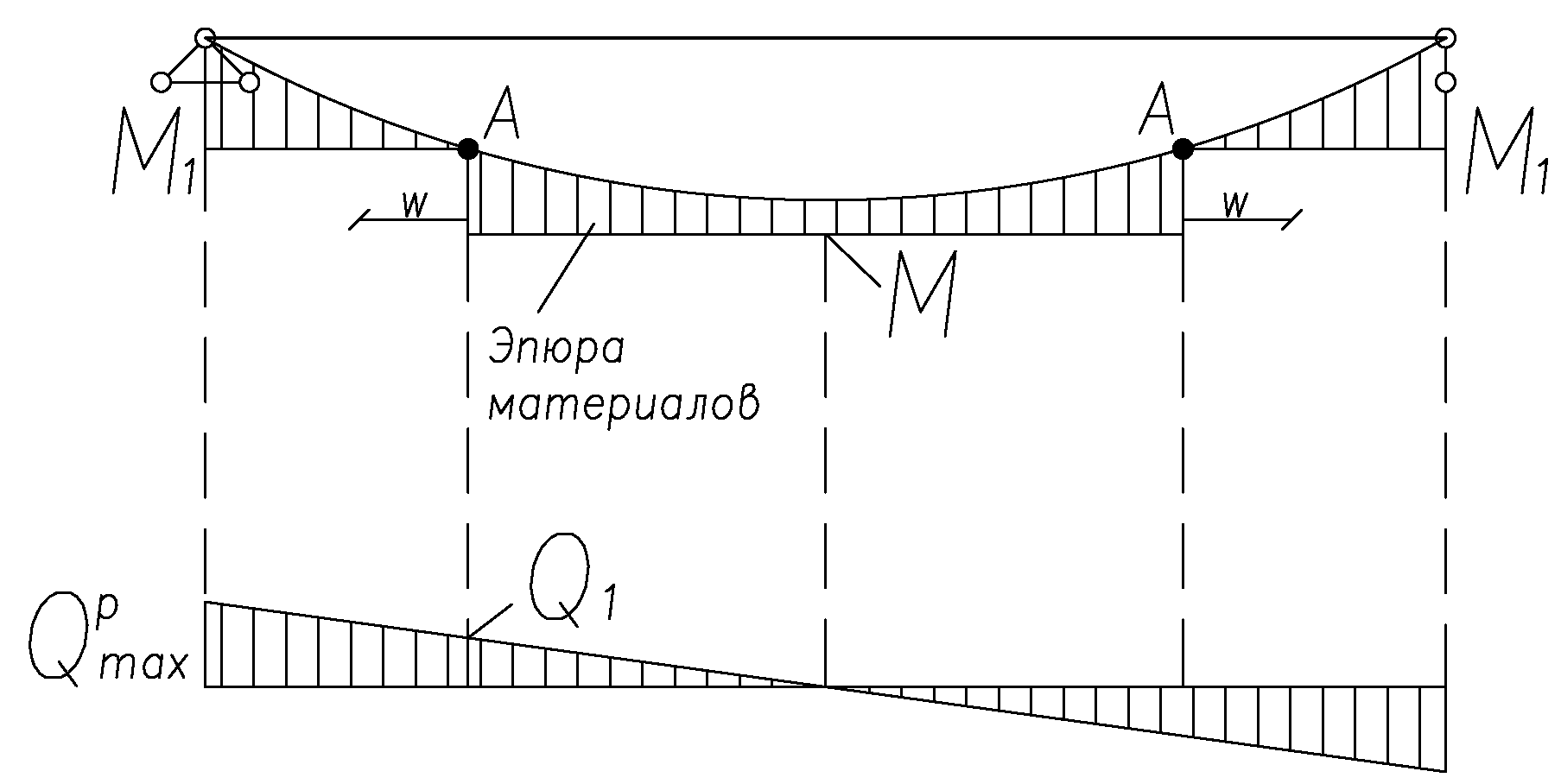 А- теоретическая точка обрыва. 3) Так как точке теоретического обрыва арматуры обрывать опасно, следует завести обрываемую арматуры за эти точки на величину 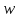 . .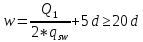 , где 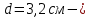 диаметр обрываемой арматуры; диаметр обрываемой арматуры;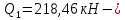 поперечная сила, действующая в точке теоретического обрыва; поперечная сила, действующая в точке теоретического обрыва;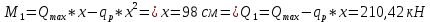 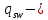 поперечная сила, воспринимаемая одним стрежнем поперечной арматуры; поперечная сила, воспринимаемая одним стрежнем поперечной арматуры;Так как в ригеле принимаем поперечную арматуру конструктивно 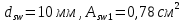 , то , то 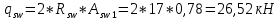 ,где 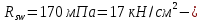 для арматуры А240. для арматуры А240.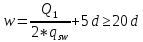 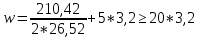 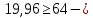 условие не выполняется, следовательно условие не выполняется, следовательноПринимаем 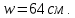 |
