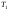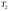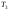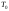готовая работа 7 варианта. Идентификация дискретной динамической модели по имитационной модели объекта
 Скачать 257.18 Kb. Скачать 257.18 Kb.
|
ИДЕНТИФИКАЦИЯ ДИСКРЕТНОЙ ДИНАМИЧЕСКОЙ МОДЕЛИ ПО ИМИТАЦИОННОЙ МОДЕЛИ ОБЪЕКТАЦель работы: изучение методов построения дискретных динамических моделей, используемых при синтезе цифрового управления, и идентификация параметров моделей объектов регулирования, описываемых конечно-разностными уравнениями. Непрерывная модель, описывающая поведение объекта с сосредоточенными параметрами, представляет собой непрерывную функцию 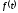 и может быть интерпретирована в виде графика (рис.1). и может быть интерпретирована в виде графика (рис.1).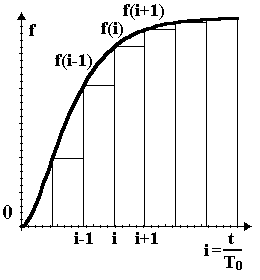 Рис.1. График функции 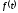 Весь диапазон времени разбивается на равные интервалы. 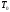 - такт квантования. Обозначим - такт квантования. Обозначим  - текущий индекс (номер) такта квантования. - текущий индекс (номер) такта квантования.При малых тактах квантования разностные уравнения можно получать из дифференциальных путем дискретизации последних [2]. В частности, дифференциалы могут приближенно заменяться правыми разностями: 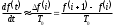 ; ;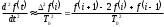 ; (1) ; (1)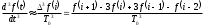 . .Таким образом можно получить производную  -го порядка в виде разностной схемы. -го порядка в виде разностной схемы.Из теории автоматического управления известно, что модели (рис.2) динамических объектов с запаздыванием в непрерывном виде могут быть представлены дифференциальными уравнениями или соответствующими передаточными функциями: 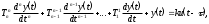 (2) (2)или 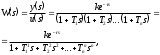 (3) (3)где 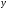 - выходной сигнал объекта; - выходной сигнал объекта;  - входной сигнал объекта; - входной сигнал объекта; 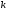 - коэффициент усиления объекта; - коэффициент усиления объекта;  - время чистого запаздывания объекта; - время чистого запаздывания объекта;  - оператор преобразования Лапласа; - оператор преобразования Лапласа; 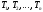 - постоянные времени объекта, по которым могут вычисляться коэффициенты - постоянные времени объекта, по которым могут вычисляться коэффициенты 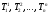 дифференциального уравнения (2): дифференциального уравнения (2):при 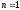 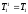 , ,при  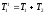 , , 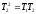 , ,при 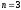 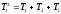 , , 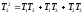 , , 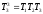 . .Описание постановки задачиТаблица 1 Исходные данные
Таблица 2 Исходные данные
Расход топлива - температура в котле является апериодическом звеном второго порядка с чистым запаздыванием и представляется в виде дифференциального уравнения второго порядка. 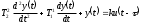 (4) (4)Математическая формулировка задачисоответствующей передаточной функции 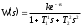 . (5) . (5)Из дифференциального уравнения (4) получим конечно-разностное: 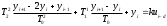 . (6) . (6)Преобразуя это уравнение, выразим из него 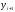 . .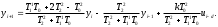 (7) (7)Введем обозначения: 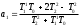 , (8) , (8)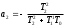 , (9) , (9)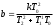 . (10) . (10)Отсюда 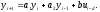 (11) (11)Уменьшая текущий индекс такта квантования на единицу в левой и правой частях уравнения (11), получим конечно-разностное уравнение второго порядка, удобное для практического использования: 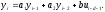 (12) (12)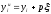 , (13) , (13)где 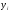 - выход объекта без помехи; - выход объекта без помехи; 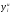 - измеряемое значение выходного сигнала с помехой - измеряемое значение выходного сигнала с помехой 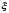 ; ; 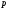 - коэффициент помехи, определяющий уровень помехи на каждом такте - коэффициент помехи, определяющий уровень помехи на каждом такте 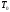 квантования; квантования; 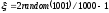 . .Для уравнения (12) начальные условия принимаются нулевыми и определяются его порядком: 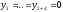 , (14) , (14)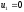 . .Если на вход имитационной модели подается единичное ступенчатое воздействие, то, начиная с такта квантования 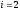 , , 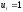 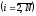 . . 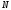 определяется временем переходного процесса определяется временем переходного процесса 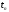 : :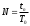 =. (15) =. (15)переходный процесс объекта регулирования 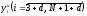 с учетом помехи с учетом помехи  . .На вход имитационной модели объекта подается единичное ступенчатое воздействие 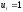 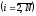 , т.е. проводится активный эксперимент. Точки кривой разгона , т.е. проводится активный эксперимент. Точки кривой разгона 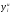 для заданного такта квантования для заданного такта квантования 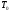 рассчитываются по уравнениям (12),(13). рассчитываются по уравнениям (12),(13).Ставится задача: по полученной на имитационной модели объекта регулирования кривой разгона найдем параметры математической модели той же структуры, то есть восстановим коэффициенты 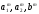 в уравнении (16): в уравнении (16):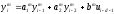 , (16) , (16)где 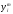 - выход восстанавливаемой модели объекта; - выход восстанавливаемой модели объекта; 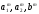 -восстанавливаемые коэффициенты модели объекта. Для решения поставленной задачи воспользуемся методом наименьших квадратов (МНК), широко применяющимся для параметрической идентификации моделей объектов регулирования. 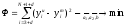 . (17) . (17)В уравнении (16) индекс  при при 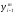 и и 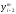 можно заменить на индекс можно заменить на индекс  , т.к. для определения , т.к. для определения 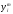 всегда известны измеренные значения всегда известны измеренные значения 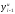 и и 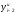 . Поэтому для любого . Поэтому для любого  -го такта квантования справедливо: -го такта квантования справедливо: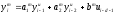 . (18) . (18)Подставив (18) в (17), получим: 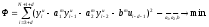 (19) (19)Так как функция 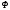 положительно определенная в силу квадратичной формы, то необходимым и достаточным условием экстремума положительно определенная в силу квадратичной формы, то необходимым и достаточным условием экстремума 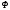 является равенство нулю первых производных по искомым параметрам: является равенство нулю первых производных по искомым параметрам: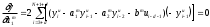 ; ;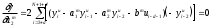 ; (20) ; (20)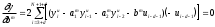 ; ;После преобразования получим: 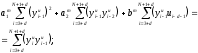 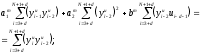 (21) (21)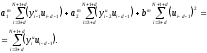 Параметры 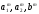 , удовлетворяющие критерию (17), находятся решением системы (21) линейных уравнений [1]. МНК в приведенной постановке со стохастическим возмущающим сигналом позволяет получить достоверные и несмещенные оценки параметров , удовлетворяющие критерию (17), находятся решением системы (21) линейных уравнений [1]. МНК в приведенной постановке со стохастическим возмущающим сигналом позволяет получить достоверные и несмещенные оценки параметров 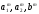 . .При равенстве нулю коэффициента помехи 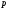 , т.е. при отсутствии возмущений на выходе имитационной модели, когда , т.е. при отсутствии возмущений на выходе имитационной модели, когда 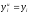 , оценки , оценки 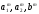 должны совпадать с должны совпадать с 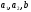 (до погрешности вычислений). (до погрешности вычислений).По полученным 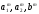 из системы (21) можно восстановить значения параметров соответствующей передаточной функции объекта (5) из системы (21) можно восстановить значения параметров соответствующей передаточной функции объекта (5) 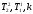 . .После получения параметров 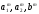 разностного уравнения (16) необходимо оценить меру соответствия полученной модели реальному объекту (имитационной модели), т.е. проверить адекватность модели объекту. разностного уравнения (16) необходимо оценить меру соответствия полученной модели реальному объекту (имитационной модели), т.е. проверить адекватность модели объекту.Адекватность устанавливается по критерию Фишера [3], для чего рассчитывается дисперсионное соотношение 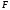 : :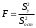 , (22) , (22)где 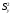 - дисперсия относительно среднего, характеризующая отклонение выхода объекта - дисперсия относительно среднего, характеризующая отклонение выхода объекта 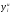 от среднего значения от среднего значения 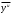 ; ; 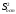 - остаточная дисперсия, характеризующая отклонение выхода модели - остаточная дисперсия, характеризующая отклонение выхода модели 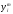 от выхода объекта от выхода объекта 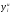 . .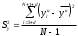 , (23) , (23)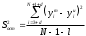 , (24) , (24)где 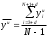 - среднее значение выхода объекта; - среднее значение выхода объекта; 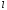 - число связей, наложенных на выборку, равное числу определяемых коэффициентов (для уравнения (16) - число связей, наложенных на выборку, равное числу определяемых коэффициентов (для уравнения (16) 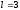 ). ).Полученное разностное уравнение (25) модели считается адекватным объекту, если расчетное значение 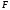 больше некоторого критического значения больше некоторого критического значения 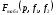 , т.е. при выполнении неравенства: , т.е. при выполнении неравенства: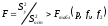 , (25) , (25)где 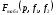 - критическое значение критерия, зависящее от чисел - критическое значение критерия, зависящее от чисел 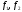 степеней свободы для дисперсии степеней свободы для дисперсии 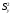 и и 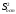 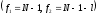 и от уровня значимости и от уровня значимости 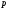 . .Критическое значение Фишера выбирается из таблиц распределения Фишера [4]. Уровень значимости принять равным 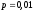 . При невыполнении условия (25) уравнение (18) модели не адекватно объекту. . При невыполнении условия (25) уравнение (18) модели не адекватно объекту.Схема алгоритма решения Рис. 4. Схема алгоритма решения задачи  Рис. 4. Продолжение 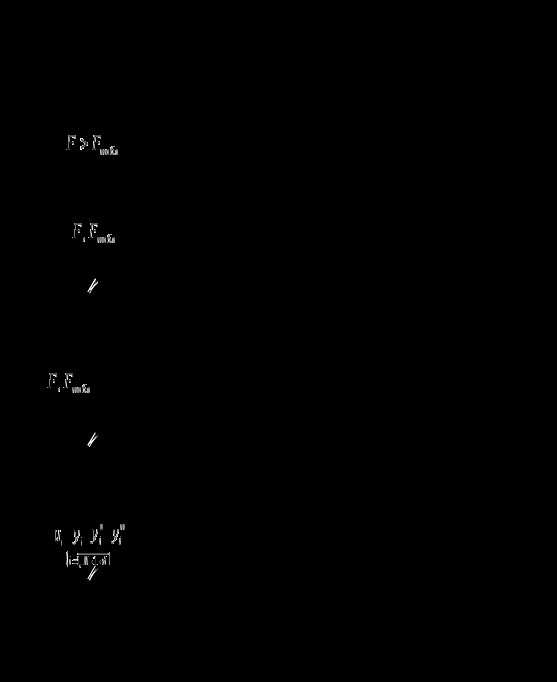 Рис.4. Окончание Распечатка программы и результатов расчетовГрафики переходных процессов объекта 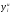 (при наличии помехи и без нее) и модели (при наличии помехи и без нее) и модели 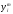 (разных порядков) (разных порядков) Анализ полученных результатов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||