|
|
лекция 3. Идентификация объекта управления методом
Идентификация объекта
управления методом
регрессионного анализа
] Линейная регрессия
С помощью корреляционного анализа можно установить, насколько тесна связь между двумя или более случайными величинами. Однако в дополнение к этому желательно располагать моделью зависимости, которая позволяла бы предсказывать значение некоторой величины по заданным значениям других величин
Определить форму связи - значит выявить механизм получения зависимой случайной переменной При изучении статистических зависимостей, форму связи можно охарактеризовать функцией регрессии, которая может быть линейной, квадратной, показательной ит.д.
Услойноё математическое ожидание М(у) случайной переменной рассматриваемой как функция X. те. M(y)=f(x), называется функцией регрессии случайной переменной Y относительно X. Функция M(y)=f(x) показывает, каково будет среднее значение К если переменная X примет вполне определенное значение
Для характеристики формы связи при изучении корреляционной зависимости пользуются понятием кривая регрессии.
Кривой регрессии Y по X называется условное среднее значение случайной переменной Y, рассматриваемой как функция отХ. те. f(x).
Возникает вопрос: почему для определения кривой регрессии пользуются именно условным средним значением Ycp(x). Данное значение обладает одним замечательным свойством: о ею дает наименьшую среднюю погрешность оценки прогноза.
Если вычислить среднее значение Y в каждом интервале изменения X, нанести эти точки на поле корреляции и соединить эти точки между собой, то мы получим ломаную линию. По виду данной ломаной линии можно говорить, как в среднем меняется Y в зависимости от изменения X. Такая линия называется эмпирической линией регрессии. По ее виду можно сделать предположение о форме связи. Аппроксимированную линию называют теоретической линией регрессии (рисунок).
Линейная регрессия занимает особое место в теории корреляции. При такой форме связи у1 (л) есть линейная функция от .г, т. е.
y'fx) = ОД
где аои а,-коэффициенты регрессии:
л - независимая случайная переменная
Линейная регрессия обуславливается двумерным нормальным законом распределения пары случайных переменных (avr).
Параметры в уравнении регрессии, т. е. коэффициенты регрессии, определяются по способу наименьших квадратов.
В начале XiX века Лежандр и Гаусс независимо друг от друга нашли метод определения неизвестных по результатам опыта, с помощью которого можно эффективно использовать избыточную информацию.
Условие Лежандра:
Q S(-v/
£)
- Qmin
i = l
где л*. - измеренное или опытное значение переменной величины;
Е - истинное или теоретическое значение случайной величины
Требование Лежандра заключается в том, чтобы сумма квадратов отклонений измеренных величин от истинного значения была бы минимальной.
В случае линейной регрессии принимают: х, = у., Е = у'(х).
Получается:
0= П у;-у'С'Р2 = &,„),
где у, - измеренное значение у
Минимум функции можно найти, приравняв к нулю ее первую производную.
С = Z(y-<‘О - «Iх)2 = Qmm
Находим частные производные функции Q по «ои а, и приравниваем к 0.
= -2lG’ - ао ' "1л)= 0
%
] Линейная регрессия 2
Q S(-v/ £) - Qmin i = l 5
2 Множественная линейная рецессия 10
3 Нелинейная регрессия 11
, 2 11
+ =Еух
Решая данную систему, находим аои а,.
X уV
)2
2 Множественная линейная рецессия
Зависимость между несколькими переменными величинами принято выражать уравнением множественной регрессии (может быть линейной и нелинейной). В простейшем виде множественная линейная регрессия выражается уравнением с двумя независимыми переменными величинами (x;z):
у = a + bx+cz
Для нахождения параметров этого уравнения (по способу наименьших квадратов) применяют следующую систему уравнений:
f ап + /?Хл + z = Xy
(1^Х+Ь^Х“ 4- c£.¥Z = ХУУ
< «X 2 4- li^XZ 4- CX 2“ = X У2
3 Нелинейная регрессия
В качестве уравнения регрессии может быть использовано уравнение прямой линии, многочлен А-ой степени или какая-то другая функция. В первом случае связь называется линейной, в остальных - нелинейной.
Уравнение параболы второго порядка имеет вид:
, 2
у = а+Ьх+сх
Для данного уравнения система нормальных уравнений имеет вид:
<¥/// +/?£д + сХ-х^ = Ху
•< аХ л*+ЬХ А" + сХ -V‘? = X *У
+ сХ*4 = Xyv2
Уравнение гиперболы первого порядка имеет вид:
Для данного уравнения система нормальных уравнений имеет вид:
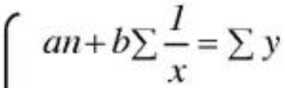
Л* „2
Совместное решение этой системы относительно параметров а и b приводит к следующим формулам:
] Линейная регрессия 2
Q S(-v/ £) - Qmin i = l 5
2 Множественная линейная рецессия 10
3 Нелинейная регрессия 11
, 2 11
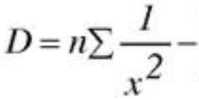  

где
- определитель системы;
х- значение независимой переменной величины;
у - значение зависимой переменной величины;
п- число членов ряда регрессии.
По изложенной выше методике регрессионный анализ применяют для обработки результатов пассивного эксперимента^ те. эксперимента, в котором невозможно назначать и поддерживать на выбранном уровне значения неслучайной величины. Более эффективным является активный эксперимент, позволяющий применять математическое планирование эксперимента и тем самым уменьшать время и число опытов |
|
|
 Скачать 18.75 Kb.
Скачать 18.75 Kb.