ОСНОВЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ПРО. Практическая работа 1 Запишите вид парной линейной регрессии. Дайте определение всем входящим в нее элементам
 Скачать 99.02 Kb.
|
|
Практическая работа 1 1. Запишите вид парной линейной регрессии. Дайте определение всем входящим в нее элементам. В случае парной линейной регрессии для данных генеральной совокупности связь между независимой переменной (факториальным признаком) X и зависимой переменной (результативным признаком) Y описывает модель  где  - свободный член прямой парной линейной регрессии, - коэффициент направления прямой парной линейной регрессии, - случайная погрешность,N - число элементов генеральной совокупности. 2. В чем суть метода наименьших квадратов? Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b 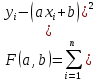 принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.3. Дайте интерпретацию параметров b1 и b0 линейной модели. Покажите их графическое представление. Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение парной регрессии достаточно распространенным в эконометрических исследованиях. Формально a – значение y при x = 0. Если x не имеет и не может иметь нулевого значения, то такая трактовка свободного члена a не имеет смысла. Параметр a может не иметь экономического содержания. Попытки экономически интерпретировать его могут привести к абсурду, особенно при a< 0. Интерпретировать можно лишь знак при параметре a. Если a> 0, то относительное изменение результата происходит медленнее, чем изменение фактора. 4. Что оценивает линейный коэффициент корреляции? Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). 5. Приведите примеры нелинейных моделей по объясняющей переменной x. Примером нелинейной регрессии по включаемым в нее объясняющим переменным могут служить следующие функции: 1. полиномы разных степеней 2. равносторонняя гипербола 6. Что понимается под линеаризацией нелинейной модели? Сущность метода линеаризации заключается в том, что нелинейную функцию заменяют некоторой линейной и затем по уже известным правилам находят числовые характеристики этой линейной функции, считая их приближенно равными числовым характеристикам нелинейной функции. 7. Каким показателем характеризуется теснота связи факторов для нелинейной модели? Каковы свойства этого показателя? Мерой интенсивности связи при нелинейных соотношениях между переменными служит индекс корреляции. Индекс корреляции рассчитывается, когда выбрана конкретная нелинейная зависимость между переменными, построена эта зависимость и по ней определены теоретические значения результирующей переменной “ŷ”.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
