Для ЖУкова Б.А. Идз 12. 3 Вариант 12. Разложить в ряд Фурье периодическую (с периодом 2) функцию f(X) заданную на отрезке 12
 Скачать 166.5 Kb.
|
|
ИДЗ 12.3 – Вариант 12. 1. Разложить в ряд Фурье периодическую (с периодом ω=2π) функцию f(x) заданную на отрезке [-π; π] 1.12.  Вычислим коэффициенты Фурье:   Принимаем   Подставляя найденные коэффициенты в ряд: Получаем: 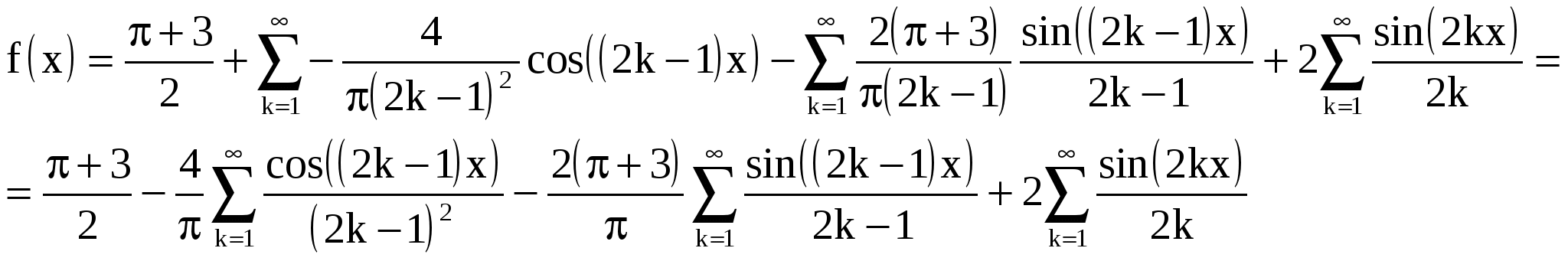 2. Разложить в ряд Фурье функцию f(x), заданную в интервале (0; π) продолжив (доопределив) ее четным и нечетным образом. Построить графики для каждого продолжения. 2.12. f(x) =  Продолжим данную функцию чётным образом. Тогда: 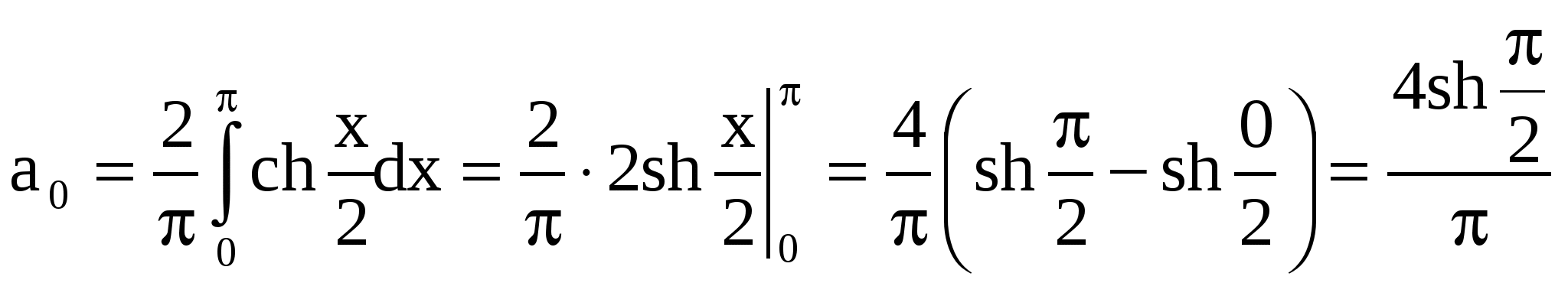   ;    Следовательно, разложение данной функции по косинусу имеет вид  Продолжим данную функцию нечетным образом. Тогда:     Следовательно, разложение данной функции по синусам имеет вид  3. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом w=2l 3.12. f(x) = 3 – x, –2 < x < 2, l= 2 Раскладываем в ряд Фурье по формуле:  Найдем коэффициенты Фурье  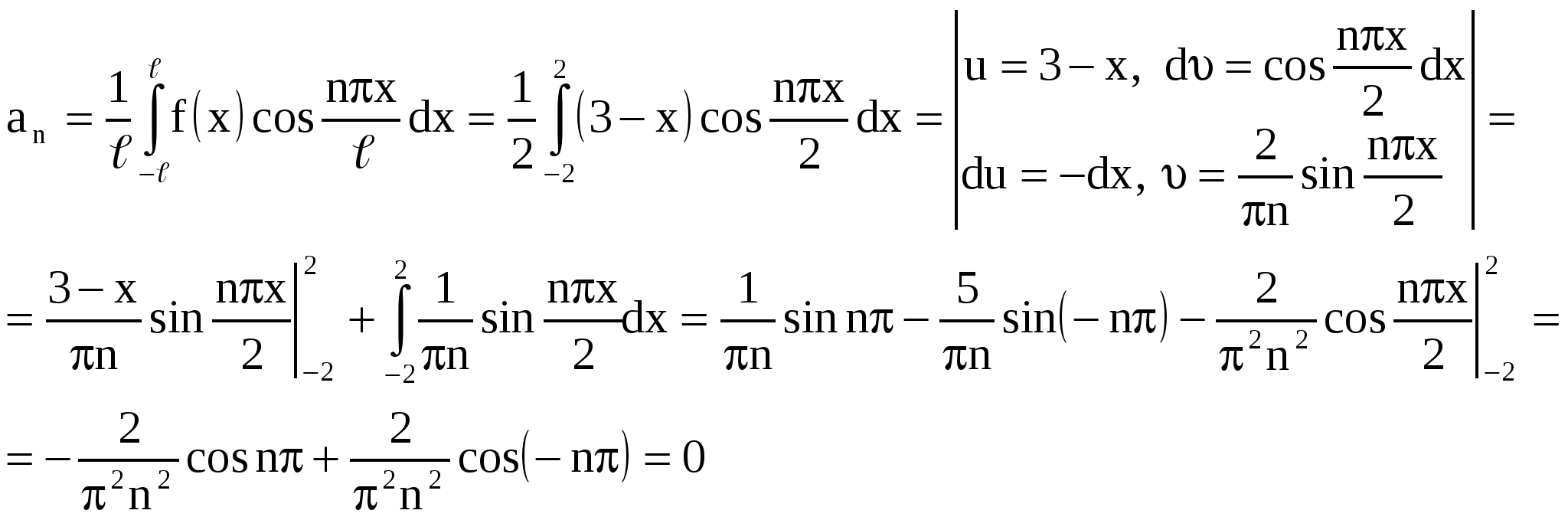  Тогда  4. Разложить в ряд Фурье функцию, заданную графически. 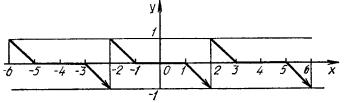 4.12. На интервале xє[−2; −1] графиком функции является прямая, проходящая через точки O1(−2; 1); O2(−1; 0) Составим уравнение  На интервале xє[−1; 1] графиком функции является прямая y = 0. На интервале xє[1; 2] графиком функции является прямая, проходящая через точки O3(1;0); O4(2; −1), Составим уравнение  Запишем аналитическое выражение данной функции: 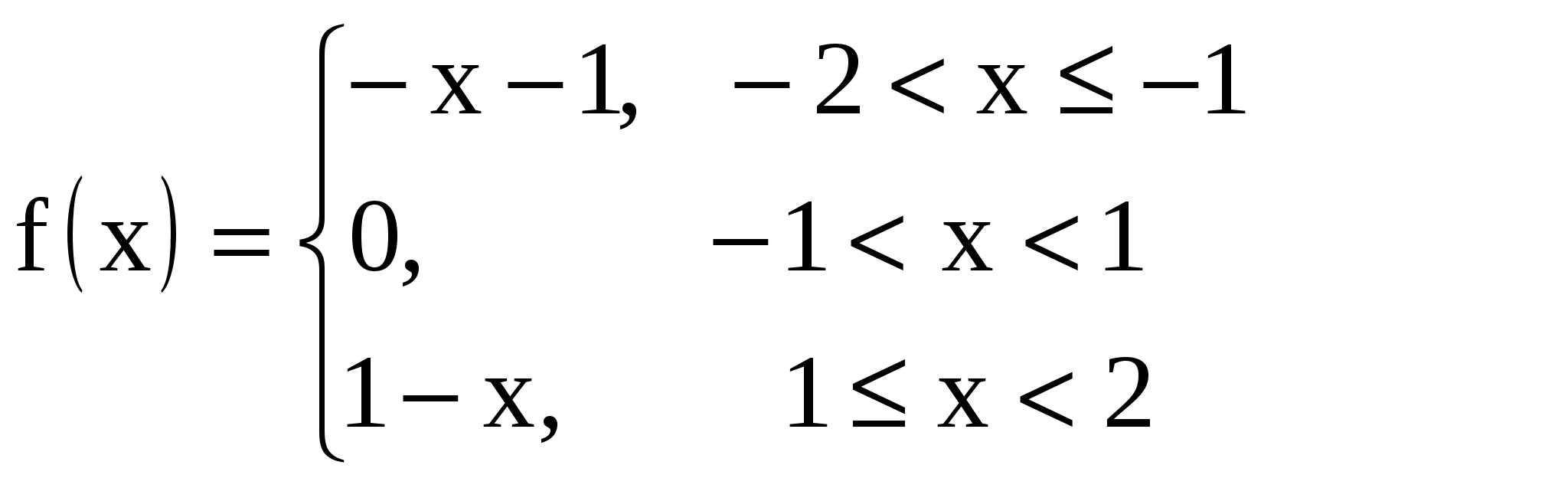  Функция является нечетной, а значит, раскладывается в ряд Фурье только по синусам:  Найдем коэффициенты Фурье 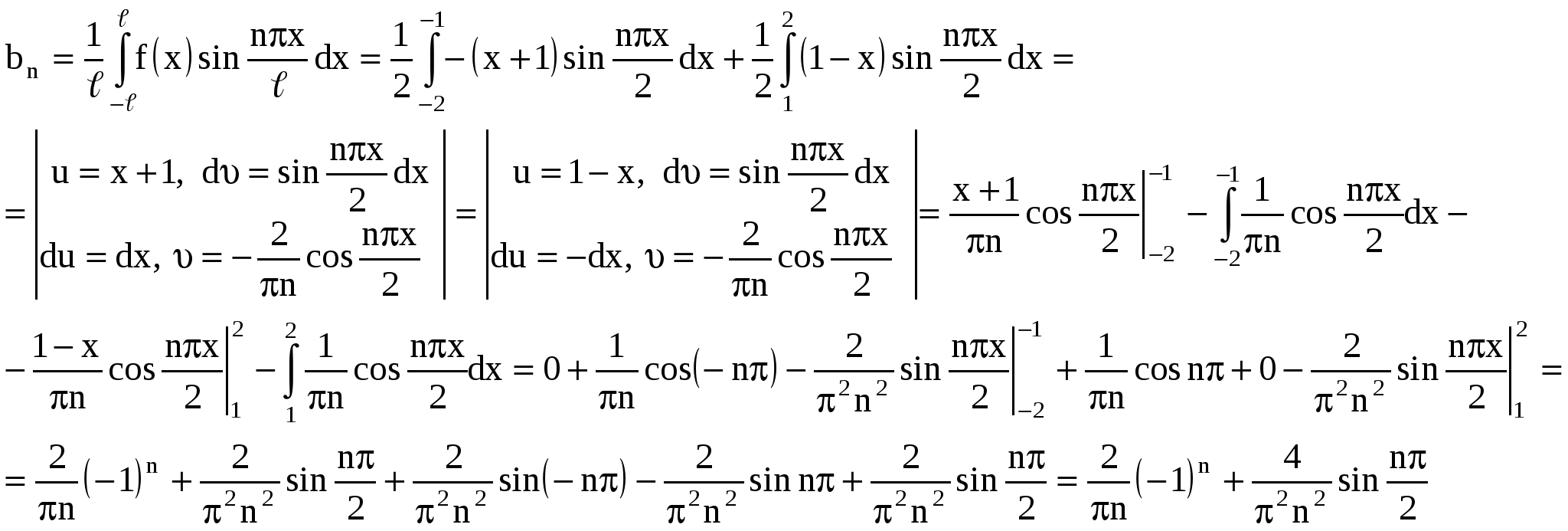  5. Воспользовавшись разложением функции f(x) в ряд Фурье в указанном интервале, найти сумму данного числового ряда. 5.12.   Так как функция четная, значит, раскладывается в ряд Фурье только по косинусам:  Найдем коэффициенты Фурье  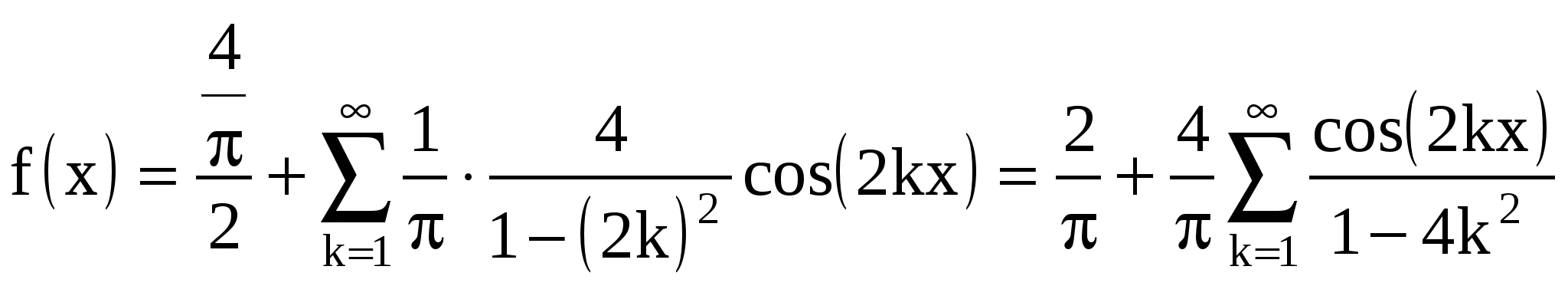 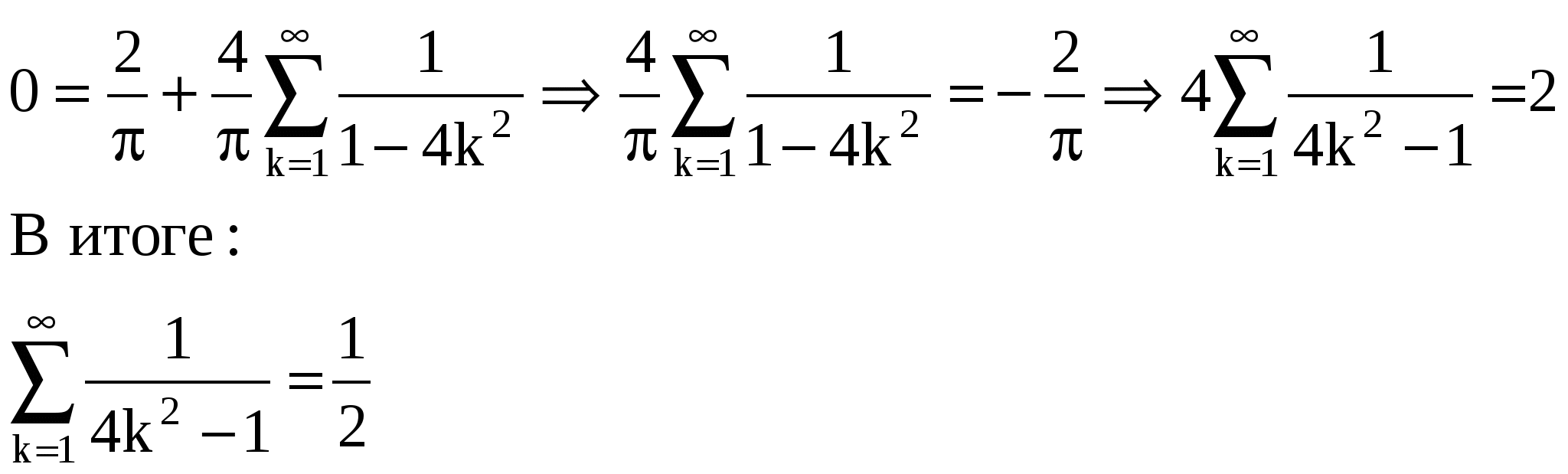  Пусть x = 0, |