Идз2. Идз 2 Вариант 0 Даны векторы a,b
 Скачать 71.96 Kb. Скачать 71.96 Kb.
|
 ИДЗ 2.2 – Вариант 0 1. Даны векторы a,b и c. Необходимо: а) вычислить смешанное произведение трех векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение двух векторов; г) проверить, будут ли коллинеарны или ортогональны два вектора; д) проверить, будут ли компланарны три вектора. 1.0 a = 3i – 2j + k, b = 3i – 5j – k, c = 2i + 4j – 3k; а) 2a, –2b, c; б) b, –2c; в) 4a, 2c; г) 2b, c; д) a, –3b, 2c. а) вычислить смешанное произведение трех векторов 2a, –2b, c; Так как, то 2a = 6i – 4j + 2k, –2b = –6i + 10j + 2k, c = 2i + 4j – 3k Вычисляем по правилу треугольника: 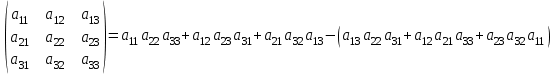 Находим смешанное произведение 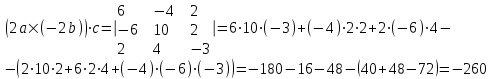 б) найти модуль векторного произведения b, –2c Поскольку b = 3i – 5j – k, –2c = –4i – 8j + 6k Векторное произведение 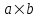 выражается через координаты данных векторов а и b следующим образом: выражается через координаты данных векторов а и b следующим образом: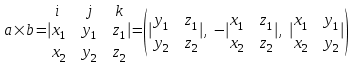 Находим векторное произведение 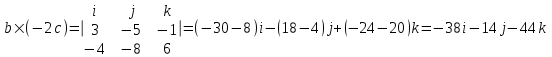 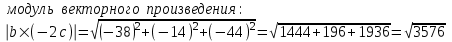 в) вычислить скалярное произведение двух векторов 4a, 2c Находим 4a = 12i – 8j + 4k, 2c = 4i + 8j – 6k Скалярное произведение двух векторов находим по формуле  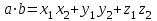 Скалярное произведение двух векторов: 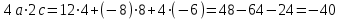 г) проверить, будут ли коллинеарны или ортогональны два вектора 2b, c Так как 2b = 6i – 10j – 2k, c = 2i + 4j – 3k и 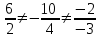 , то векторы 2b и c не коллинеарны, , то векторы 2b и c не коллинеарны, поскольку 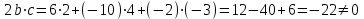 , то векторы 2b и c неортогональны. , то векторы 2b и c неортогональны. д) проверить, будут ли компланарны три вектора a, –3b, 2c. Векторы a, b, c компланарны, если abc=0. Вычисляем a = 3i – 2j + k, –3b = –9i + 15j + 3k, 2c = 4i + 8j – 6k 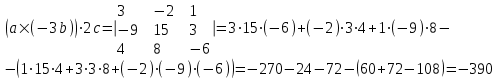 т.е. векторы a, –3b, 2c не компланарны. 2. Вершины пирамиды находятся в точках A, B, C и D. Вычислить: а) площадь указанной грани; б) площадь сечения, проходящего через середину ребра l и две вершины пирамиды; в) объем пирамиды ABCD. 2.0 A(2, –3, –1), B(–3, 1, 4), C(3, 2, 5), D(–2, –4, 3); а) ACD; б) l=AB, C и D а) площадь указанной грани ACD Известно, что 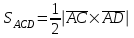 Находим: Находим: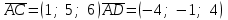 Векторное произведение 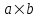 выражается через координаты данных векторов а и b следующим образом: выражается через координаты данных векторов а и b следующим образом: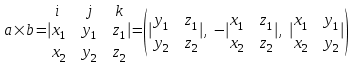 Вычисляем: 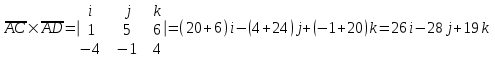 Модуль вектора определяем выражением 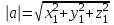 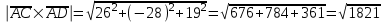 Окончательно имеем: 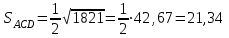 б) площадь сечения, проходящего через середину ребра AB и две вершины пирамиды C и D; A(2, –3, –1), B(–3, 1, 4), C(3, 2, 5), D(–2, –4, 3); Находим точку середины ребра BD 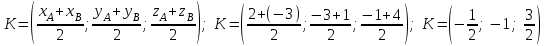 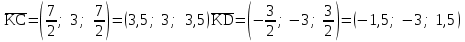 Площадь сечения находим по формуле: 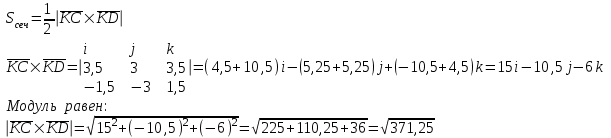 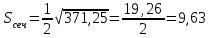 в) объем пирамиды ABCD Поскольку 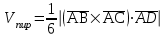  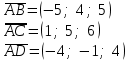 Находим смешанное произведение векторов: 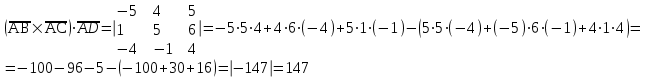 Тогда объем пирамиды ABCD 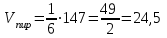 3. Сила F приложена к точке А. Вычислить: а) работу силы F в случае, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку В; б) модуль момента силы F относительно точки В. 3.0 F = (3, –2, 1), A(3, 3, 2), B(5, 1, –3) а) работу силы F в случае, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку В; Так как 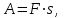 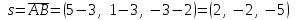 , то , то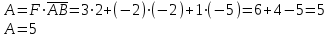 б) модуль момента силы F относительно точки В. Момент силы 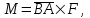 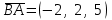 Векторное произведение 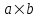 выражается через координаты данных векторов а и b следующим образом: выражается через координаты данных векторов а и b следующим образом: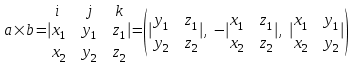 Вычисляем: 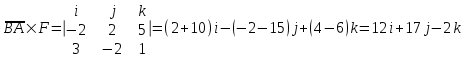 Модуль определяем выражением 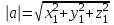 Следовательно модуль момента силы F относительно точки В. 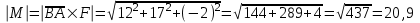 |
