физика. физика часть а. II. Тестовые задания Кинематика поступательного и вращательного движения материальной точки 1
 Скачать 1.6 Mb. Скачать 1.6 Mb.
|
|
240. Материальная точка совершает механические колебания по закону 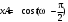 . Максимальное ускорение точки равно … . Максимальное ускорение точки равно …1. 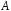 2. 2. 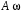 3. 3. 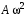 4. 4. 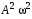 5. 5. 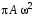 241. Середина струны колеблется с частотой 200 Гц и с амплитудой 3 мм. Наибольшее ее ускорение равно…км/с2. 1. 0,12 2. 5,3 3. 4,7 4. 12 5. 6 220. Материальная точка совершает гармонические колебания. Если максимальное смещение и максимальная скорость точки составляет соответственно 10 см и 20 см/с, то ее максимальное ускорение равно … м/с2. 1. 0,1 2. 0,2 3. 0,4 4. 2 5. 4 242. Уравнение движения материальной точки массой m = 10 г дано в виде 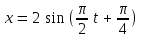 , см. Максимальная сила, действующая на материальную точку равна … мН. , см. Максимальная сила, действующая на материальную точку равна … мН.1. 49 2. 0,12 3. 0,31 4. 0,49 5. 20 243. Уравнение колебания материальной точки массой 10 г имеет вид 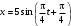 , см. Максимальная сила, действующая на точку, равна … мкН. , см. Максимальная сила, действующая на точку, равна … мкН.1. 197 2. 308 3. 500 4. 985 5. 1970 244. Точка совершает гармонические колебания согласно уравнению 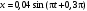 (м). Максимальная сила, действующая на точку, равна 1,5 мН. Полная энергия точки равна … мкДж. (м). Максимальная сила, действующая на точку, равна 1,5 мН. Полная энергия точки равна … мкДж.1. 60 2. 40 3. 30 4. 15 5. 12 145. Тело массой 1 кг совершает колебания вдоль оси х. Уравнение его колебаний имеет вид 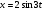 . Кинетическая энергия тела определяется выражением … . Кинетическая энергия тела определяется выражением …1. 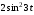 2. 2. 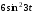 3. 3. 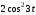 4. 4. 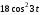 5. 5. 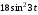 246. Начальная фаза синусоидального колебания материальной точки 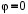 . Скорость точки будет равна половине ее максимальной скорости через долю периода Т, равную … . Скорость точки будет равна половине ее максимальной скорости через долю периода Т, равную … 1. 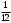 2. 2. 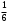 3. 3. 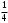 4. 4.  5. 5. 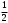 247. Математический маятник длиной 1 м установлен в лифте, опускающемся вниз с ускорением 2,5 м/с2. Период колебания маятника равен … с. 1. 1,6 2. 1,8 3. 2,0 4. 2,3 5. 3,2 248. К пружине подвешен груз массой 10 кг. Если под влиянием силы 9,8 Н пружина растягивается на 1,5 см, то период вертикальных колебаний груза равен…с. 1. 0,78 2. 0,96 3. 1,2 4. 1,8 5. 2,58 249. Спиральная пружина обладает жесткостью k = 25 Н/м. Чтобы за время t = 1 мин совершалось 25 колебаний, к пружине надо подвесить тело массой … кг. 1. 0,001 2. 0,11 3. 1,66 4. 3,65 5. 9,55 250. Дифференциальное уравнение свободных колебаний без затухания имеет вид (ω02, k, m, β, r – постоянные, не равные нулю) … 1. 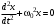 2. 2. 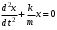 3. 3. 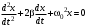 4. 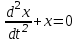 5. 5. 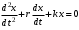 1. 3, 5 2. 1, 4 3. 2, 4 4. 1, 2 5. 1, 2, 4 251. Дифференциальное уравнение свободных затухающих механических колебаний имеет вид … 1. 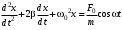 2. 2. 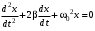 3. 3. 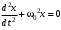 4. 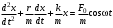 5. 5. 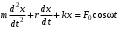 252. Дифференциальное уравнение вынужденных механических колебаний имеет вид … 1. 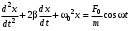 2. 2. 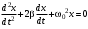 3. 3. 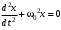 4. 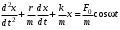 5. 5.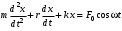 1. 1, 2 2. 2, 4 3. 2, 3, 5 4. 1, 4, 5 5. 3, 4, 5 253. Период колебаний физического маятника равен 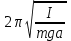 . В этой формуле l – это … . В этой формуле l – это …1. длина маятника 2. ширина маятника 3. длина оси маятника 4. расстояние от оси до центра масс 5. нет верного ответа 255. Математический маятник длиной L1 = 40 см и физический маятник в виде тонкого прямого стержня длиной L2 = 80 см и массой 0,5 кг синхронно колеблются около одной и той же горизонтальной оси. Приведенная длина физического маятника равна … см. 1. 5,44 2. 80 3. 40 4. 32 5. 2,72 256. Обруч диаметром D = 1 м висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Приведенная длина обруча равна … м. 1. 2,0 2. 1,5 3. 1,0 4. 0,5 5. 0,10 257. Однородный тонкий стержень длиной 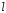 совершает колебания около горизонтальной оси, проходящей через конец стержня. Приведенная длина маятника равна… совершает колебания около горизонтальной оси, проходящей через конец стержня. Приведенная длина маятника равна… 1. 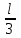 2. 2. 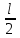 3. 3. 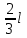 4. l 5. 4. l 5. 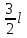 258. Тонкий обруч, подвешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус обруча равен 30 см. Период колебаний равен … с. 1. 1 2. 1,1 3. 1,55 4. 1,8 5. 0,3 259. Диск радиуса R колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Период его колебаний равен … 1. 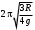 2. 2. 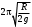 3. 3. 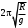 4. 4. 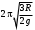 5. 5. 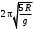 260. Два диска одинакового радиуса и массами 2 и 8 кг соответственно совершают колебания относительно оси, касательной к их поверхности. Периоды колебаний дисков относятся как … (ответ поясните). 1. 1:2 2. 1:1 3. 2:1 4. 1:4 5. 4:1 261. Коэффициент затухания колебаний маятника можно увеличить … 1. уменьшив массу колеблющегося тела 2. уменьшив начальную амплитуду колебания 3. увеличив массу колеблющегося тела 4. увеличив начальную амплитуду колебания 5. уменьшив начальную амплитуду колебаний и вязкость среды 262. Коэффициент затухания – это физическая величина, … 1. показывающая во сколько раз уменьшается амплитуда колебаний за период 2. обратная времени, по истечении которого амплитуда колебаний уменьшается в «е» раз 3. обратная числу колебаний, по завершению которых амплитуда колебаний уменьшается в «е» раз 4. обратная числу колебаний, по завершению которых амплитуда колебаний уменьшается до нуля 5. обратная времени, по истечении которого амплитуда колебаний уменьшается до нуля 263. Шарик радиусом 10 см и массой 0,5 кг, подвешенный к нити длиной 20 см, совершает затухающие колебания в среде с коэффициентом затухания 2 кг·с-1. Коэффициент сопротивления среды равен … с-1. 1. 0,14 2. 1 3. 2 4. 4 5. 8 264. За 10 с амплитуда пружинного маятника массой m= 0,1 кг уменьшилась в е раз. Коэффициент затухания 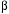 и коэффициент сопротивления среды и коэффициент сопротивления среды  равны … равны …1. 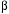 = 1; = 1;  = 0,01 кг·с-1 = 0,01 кг·с-12. 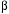 = 0,1; = 0,1;  = 0,1 кг·с-1 = 0,1 кг·с-13. 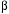 = 0,1; = 0,1;  = 0,02 кг·с-1 = 0,02 кг·с-14. 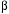 = 0,01; = 0,01;  = 0,04 кг·с-1 = 0,04 кг·с-15. 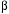 = = 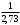 ; ;  = 0,02 кг·с-1 = 0,02 кг·с-1265. Период Т затухающих колебаний груза массой m на пружине жесткостью k можно рассчитать по формуле … ( 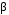 – коэффициент затухания, – коэффициент затухания, 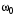 – циклическая частота свободных незатухающих колебаний колебательной системы). – циклическая частота свободных незатухающих колебаний колебательной системы).1. 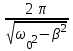 2. 2. 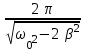 3. 3. 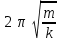 4. 4. 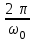 5. 5. 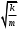 266. За время релаксации амплитуда затухающих колебаний … 1. увеличивается в 2 раза 2. уменьшается в 2 раза 3. увеличивается в e раз 4. уменьшается в e раз 5. не изменяется 267. Если период колебаний 2,5 с, коэффициент затухания 2 с-1, то логарифмический декремент затухания равен …. 1. 0,8 2. 1,25 3. 5 4. 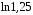 5. 5. 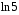 268. За один период амплитуда колебаний математического маятника с логарифмическим декрементом затухания 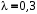 уменьшится в …раз. уменьшится в …раз.1. 0,3 2. 0,37 3. 1,35 4. 2,73 5. 3,33 269. Логарифмический декремент затухания – это физическая величина, … 1. показывающая во сколько раз уменьшается амплитуда колебаний за период 2. обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается до нуля 3. обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается в «е» раз 4. обратная промежутку времени, за которое амплитуда колебаний уменьшается в «е» раз 5. обратная промежутку времени, за которое амплитуда колебаний уменьшается до нуля 270. Логарифмический декремент затухания колебаний маятника λ. Если амплитуда колебаний уменьшилась в n раз, то маятник совершил … колебаний. 1. 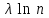 2. 2. 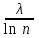 3. 3. 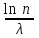 4. 4. 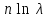 5. 5. 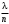 271. Период затухающих колебаний Т = 4 с. Добротность системы Q = 5. Логарифмический декремент затухания λ равен … 1. 20 2. 1,57 3. 1,25 4. 0,80 5. 0,63 272. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания λ = 1,6. Добротность системы (Q) равна … 1. 0,4 2. 0,79 3. 1,96 4. 2,5 5. 6,4 273. При сложении двух одинаково направленных колебаний, описываемых соответственно уравнениями  м и м и  м получается колебание с амплитудой А, равной … м. м получается колебание с амплитудой А, равной … м.1.  2. 2.  3. 3. 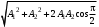 4. 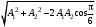 5. 5. 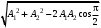 274.Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной … 1. 0 2. 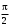 3. 3. 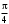 4. 4. 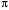 5. 5. 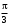 275. При сложении одинаково направленных гармонических колебаний одной частоты с амплитудами 10 см и 6 см, возникло колебание с амплитудой 14 см. Разность фаз складываемых колебаний равна … град. 1. 30 2. 45 3. 60 4. 90 5. 120 276. Складываются два колебания одинакового направления с амплитудами А1 = 3 см и А2 = 4 см. Чему равна разность фаз этих колебаний 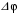 (в радианах), если амплитуда А результирующего колебания равна 5 см? (в радианах), если амплитуда А результирующего колебания равна 5 см?1. 0 2. 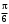 3. 3. 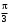 4. 4. 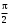 2. 2. 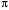 277. Складываются два колебания одинакового направления с амплитудами А1 = 3 см и А2 = 4 см. Амплитуда А результирующего колебания равна 6,1 см. Разность фаз складываемых колебаний равна … рад. 1. 0 2. 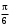 3. 3. 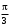 4. 4. 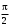 5. 5. 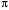 278. Складываются два колебания одинакового направления с амплитудами А1 = 3 см и А2 = 4 см и разностью фаз  рад. Амплитуда А результирующего колебания равна … см. рад. Амплитуда А результирующего колебания равна … см.1. 1,0 2. 6,08 3. 6,77 4. 5,0 5. 7 279. Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами  . При разности фаз . При разности фаз  амплитуда результирующего колебания равна … амплитуда результирующего колебания равна … 1.  2. 2.   3. 0 4. 3. 0 4.   5. 5. 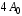 280. Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами 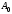 . При разности фаз . При разности фаз 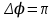 амплитуда результирующего колебания равна … амплитуда результирующего колебания равна … 1. 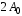 2. 2. 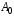 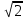 3. 0 4. 3. 0 4. 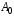 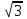 5. 5.  |
