Бетонның жылу өткізгіштік қасиеті. Шекаралық және бастапқы шарттары. Отчет Умит. ылыми зерттеу жмысы бойынша 1семестрге есебі магистрант
 Скачать 304 Kb.
|
|
Ф.7.28-03 М.О.ӘУЕЗОВ атындағы Оңтүстік Қазақстан университеті ЖОҒАРЫ ОҚУ ОРНЫНАН КЕЙІНГІ БІЛІМ БЕРУ ИНСТИТУТЫ «СӘУЛЕТ, ҚҰРЫЛЫС ЖӘНЕ КӨЛІК» факультеті «Құрылыс және құрылыс материалдары» кафедрасыҒылыми зерттеу жұмысы бойынша 1-семестрге ЕСЕБІ Магистрант: Рахымхан Үміт Уәлиханқызы Білім беру бағдарламасы:____7М07320-Құрылыс______________ Группа: МСМ-21-3нк Тақырып : Жоғары температура әсерінен бетон және темірбетон конструкцияларындағы жылу жылжымалықты есепке алу Шымкент 2021 Мазмұны Кіріспе 3 1. Әдебиеттік шолу; Мәселе жағдайын талдау және зерттеулер мақсаты 4 1.1 Бетонның жылуөткізгіштігі. Бетонның жылуөткізгіштік теориясының негізгі теңдеулері 5 1.2 Шекаралық және бастапқы шарттары 12 1.3 Бетонның жылуөткізгіштік қасиеттері 18 1.4 Тарау бойынша қорытынды тұжырымдар 19 Пайдаланылған әдебиеттер тізімі 20 Кіріспе Бетон салыстырмалы түрде жоғары қысым күші (ол салмақ кезінде жарылмайды), бірақ айтарлықтай төмен беріктік шегі (тартқан кезде жарылып кетеді). Сығымдау беріктігі, әдетте, бетон қалыптастыру кезінде су мен цементтің қатынасында бақыланады, ал созылуға беріктік темірбетон жасау үшін қоспалармен, көбінесе болатпен жоғарылайды. Басқаша айтқанда, біз бетонды құмнан (бұл ұсақ толтырғыш), балласттан (ол ірі толтырғыштан), цементтен (байланыстырушы деп атауға болады) және судан (бұл қоспа) тұрады деп айтуға болады. Темірбетон бетонның ең кең таралған түрі болып табылады. Арматура көбінесе болаттан жасалған арматура (тор, спираль, штангалар және басқа формалар). Құрылымдық талшықтар әртүрлі материалдардан алуға болады. Бетон да болуы мүмкін алдын-ала басылған (төмендету созылу кернеуі) ішкі болат кабельдерін (сіңірлерін) қолдана отырып, мүмкіндік береді сәулелер немесе ұзағырақ тақталар аралық тек темірбетонға қарағанда практикалық сияқты жабдықпен жүргізілсе, қолданыстағы бетон конструкцияларын тексеру бұзбайды Шмидт балғасы, бұл кейде өрістегі салыстырмалы бетон күштерін бағалау үшін қолданылады. Бетонның максималды беріктігіне су-цементтілік қатынасы әсер етеді (д / см), құрылымдық компоненттер және араластыру, орналастыру және емдеу әдістері. Барлығы тең, су-цементтің (цементтелген) коэффициенті төмен бетон, жоғары коэффициентпен салыстырғанда мықты бетон жасайды. Цемент материалдарының жалпы саны (портландцемент, қожды цемент, позцоландар) күшке, судың сұранысына, кішіреюіне, тозуға төзімділігіне және тығыздығына әсер етуі мүмкін. Барлық бетон оның қысу күшіне ие екендігіне немесе болмайтындығына қарамастан жарылып кетеді. Шындығында, портландцемент құрамындағы жоғары қоспалар ылғалдану жылдамдығының жоғарылауына байланысты тезірек жарылып кетуі мүмкін. Бетон өзінің пластикалық күйінен қатты күйге ауысқанда, материал қысқарады. Пластикалық жиырылу жарықтары орналастырылғаннан кейін көп ұзамай пайда болуы мүмкін, бірақ егер булану деңгейі жоғары болса, олар көбінесе әрлеу жұмыстары кезінде, мысалы, ыстық ауа-райында немесе желді күнде пайда болуы мүмкін. Өте берік бетон қоспаларында (70 МПа-дан жоғары) толтырғыштың ұсату беріктігі а болуы мүмкін шектеуші фактор қысудың ең жоғары беріктігіне дейін. Жіңішке бетондарда (су-цемент коэффициенті жоғары) толтырғыштардың ұсату беріктігі соншалықты маңызды емес. Сияқты құрылымның жалпы формаларындағы ішкі күштер аркалар, қоймалар, бағаналар мен қабырғалар қысу күштері басым, едендер мен жабындар созылу күшіне ұшырайды. Сығымдау беріктігі спецификацияға және бетонның сапасына бақылау жасау үшін кеңінен қолданылады. Инженерлер өздерінің созылу (иілу) талаптарын біледі және оларды қысу беріктігі арқылы көрсетеді. Әдебиеттік шолу; Мәселе жағдайын талдау және зерттеулер мақсаты Жылуөткізгіштік құбылыстары табиғатта кеңінен таралған. Өндірісте күйдіру, балқыту, қыздыру арқылы көптеген қажетті бұйымдар алынады. Мысалы, кірпіш, қыш ыдыстар, металлургия саласында. Бұйымдар берілген талаптарға сай жасалуы үшін онда қыздыру кезінде жылудың қалай таралатынын, яғни әр түрлі нүктедегі температураны алдын-ала анықтау тиімділігі. Ішкі жылу көзі бар бірөлшемді пластинкадағы стационар емес жылуөткізгіштік процесінің сандық шешімдерін алу, компоненттерін құрудың бастапқы қадамдарын жасау. Ішкі жылу көзі бар бірөлшемді пластинкадағы стационар емес жылуөткізгіштік процессі. Бетонның жылуөткізгіштігі. Бетонның жылуөткізгіштік Жылуөткізгіштік құбылыстары табиғатта кеңінен таралған. Заманауи технология мен техниканың көптеген процестерін шешуге байланысты жылу тасымалы процессі заманауи физиканың түсініктеріне сәйкес екі көзқарас тұрғысынан зерттеледі және сипатталады. Олар феноменологиялық және статистикалық зерттеу тәсілдері. Феноменологиялық және статистикалық тәсіл қарастырылатын физикалық құбылысты тұтасымен анықтайтын параметрлердің арасындағы кейбір жалпы қатынастарды анықтауға негізделеді. Бұл зерттеу тәсілінде негізгі мәселе   түріндегі байланысын құруға келіп тіреледі. Бұл байланыстың жалпы сипаты жылу тасымалданудың үш мүмкін түрінің бірімен анықталады. Оларды біріншісі – жылуөткізгіштік жылу энергиясын физикалық жүйенің микроскопиялық элементерімен (молекулалар, иондар, электрондар) тасымалдануға қатысты. Газдардағы жылуөткізгіштік энергияны молекулалар соқтығысу арқылы, қатты денеде зат торының тербелген иондарымен және “электрондық газбен”, сұйықта – көрсетілген барлық механизмдермен іске асырылады. Микроскопиялық көлемінің қозғалысы есебінен іске асатын жылу берілу конвекция деп аталады. Конвекцияның екі түрі бар -–массаның элементтері жүйе көлемінің тығыздықтарының әртүрлі болуынан ауырлық күші өрісінде орын ауыстырғандағы еркін конвекция, және массасының орын ауыстыруы сыртқы күштердің есебінен іске асырылатын мәжбүр конвекция деп аталады. Жылу алмасудың үшінші түрі – сәулелену, денелердің электромагниттік өрістің энергиясын жұтуына, шағылуына, өткізуіне және сәулелендіруіне негізделген. Феноменологиялық заңдар жалпы сипатта, ол нақты физикалық ортаның рөлі пропорционалдық коэффициентері –сонымен бірге экспериментальді анықталатын коэффициенттермен бірге ескеріледі. Жылу тасымалдану процесстері жылуөткізгіштікпен іске астын физикалық жүйені қарастырайық. Феноменологиялық термодинамиканың жалпы процедураларына сәйкес мұндай жүйені зертеуді біз энтропия көзі үшін өрнек жазудан бастаймыз. Энтропия көзінің интенсивтілігі үшін жалпы өрнекпен, келесіні аламыз:  (1.1)жүйеде жылу өткізгіштік құбылыстар жүрмейтіндіктен, диффузия процестері жоқ, Iq және Iq1 жылу ағындары сәйкес келеді. (1.1) теңдеуге негіздеп, жылуөткізгіштік құбылысы үшін термодинамикалық күштер мен ағындарды енгізуге болады. Бұл жағдайда төмендегей болуы айқын:  термодинамикалық күш; Iq – термодинамикалық ағын. Феноменологиялық термодинамика бұдан ары енгізілген термодинамикалық күштер мен ағындардың арасында қандайда бір сызықтық қатынас болуы керек деп тұжырымдайды (феноменологиялық заң):  (1.2)Бұл феноменологиялық заң келесідей түрде жазылуы мүмкін:  (1.3)мұндағы  (1.4)(1.4) қатынасты 1822ж эксперимент жүзінде тұжырымдарды және Фурье заңы деп аталады. (1.4) өрнектегі тасымалданудың феноменологиялық коэффициентінің бірі болатын пропорционалдық коэффиенциент жылу өткізгіштіккоэффициенті деп аталады. Бұл коэффициент қарастырылатын жүйенің физикалық қасиеттерін ондағы өтіп жатқан жылуөткізгіштік процессі тұрғысынан қарастырылады.Құбылысты феноменологиялық сипаттағанда жүйенің барлық физикалық қасиеттері, басқаша айтқанда физикалық жүйелердің бір-бірінен ерекшелігі тек тасымалдау коэффициентері арқылы көрсетіледі. Көптеген жағдайларда феноменологиялық сипаттау экспериментпен жоғары дәлдікпен келеді. Екі жағдайды қарастырамыз .Оның біріншісінде 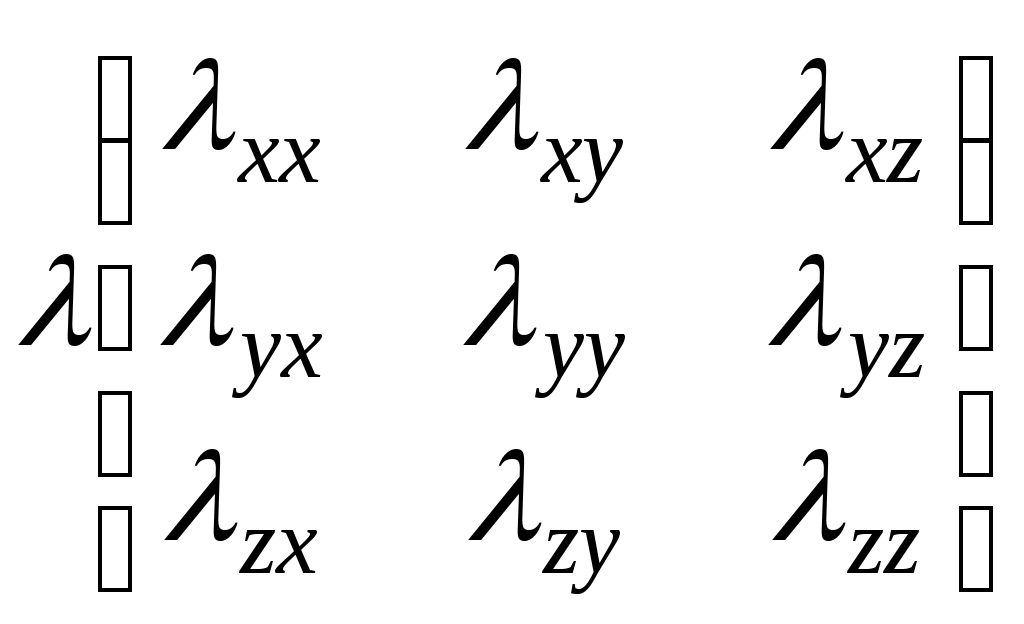 жылуөткізгіштік коэффициентінің шамасы бағытқа тәуелді емес. Iq жылу ағыны Фурье заңына сәйкес, нормальға қарама-қарсы изотермаларға (температура градиенті) бағыталған, екінші жағдайда – анизотропты орта– құбылысы күрделірек. Iq- жылу ағынының бағыты жылуөткізгіштік тензорымен анықталады,ғ бұл жағдайда коэффициенті анықталады, бұл жағдайда коэффициенті, оған сай Iq ағын ең үлкен және ең кіші мәндерге ие болатын бағыттар бар. Жылуөткізгіштік тензоры – екінші ранглі тендор – келесідей жазылады (1.5)(1.3) өрнекпен берілген Фурье заңы тензорлық түрде координаталар остеріне проекцияланып скаляр түрде келесідей жазылады: 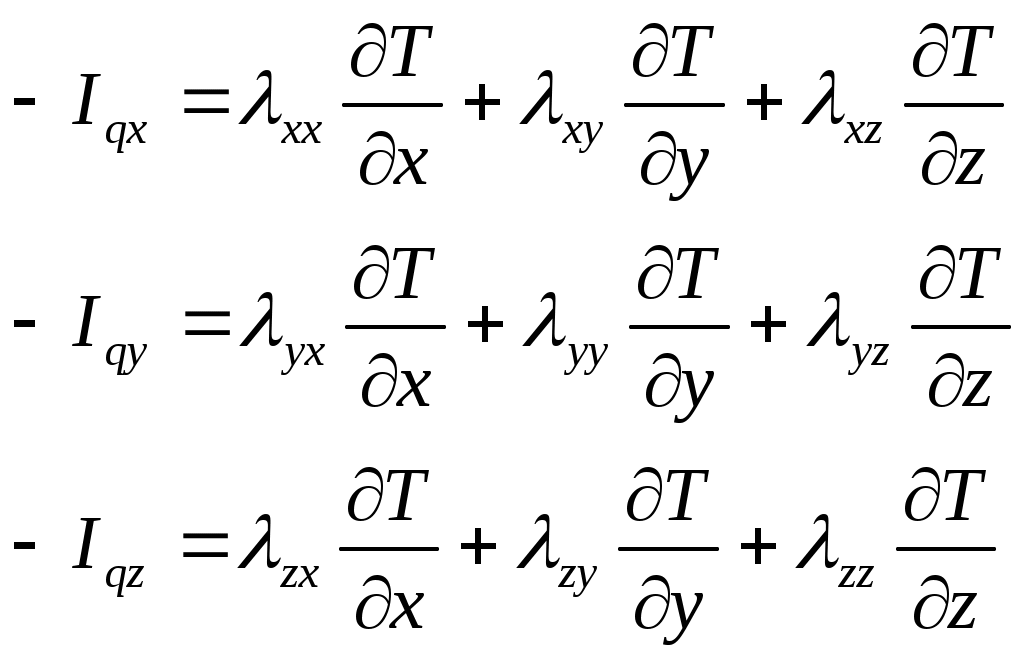 (1.6)(1.6) қатынасты координата остеріндегі түйіндес әсерлермен байланысққан жылу ағындарының проекцияларын байланыстаратын қатынас ретінде қарастыруға болады, яғни анизатропты денеде х осі бойынша жылу ағыны у және х осьтері бойынша температураның түсуіне, немесе керісінше у осіндегі температураның кемуі қалған х және у осьтері бойынша температураның кемуіне әкеледі. Бұл көзқарас тұрғысынан жүйенің (1.6) теңдеудегі коэффициентері феноменологиялық термодинамика тұжырымдағандай Онзагердің қатынастарына бағынуы керек. Яғни, сәйкес түйіндес коэффициентер тең болуы керек.  және т.с.с.1.7) қатынас тензорының симметриялық шарты болып табылды. Осылайша Онзагер қатынасынан жылуөткізгіштік тензорының - симметриялық тензор екендігі шығады. Жылуөткізгіштің бұл тензорын экспримент жүзінде Соре және Файт тетрагокальді класстың кристалдарының жылуөткізгіштіігін зерттегенде, тексерді.Осылайша, жылу ағыны мен жалпы феноменологиялық қатынасты қарастыра отырып, анизотропты орта жағдайында ағын және векторлар бірдей бағыт алмайтындығын, олардың арасындағы байланыс (1.6) қатынаспен анықталатындығы жөнінде тұжырым жасауға болады.Тек изотропты жүйе жағдайында жылуөткізгіштік тензоры скалярға келіп және жылу ағыны мен  бағыты сәйкес келеді. Жылуөткізгіштік процессін жалпы сипатағанда, ортаның анизотроптылығын ескеру математикалық қиындықтар туғызады. Техникалық маңызды материалдардың көпшілігін бірінші жуықтауда изотропты деп, ал олардың жылуөткізгіштік коэффициентерін скаляр деп санауға болады.Біз мұнда жылуөткізгіштік теңдеуін “классикалық” қорытамыз. Сақталу заңдарының бірінің теңдеуін (энергияның сақталу заңы) және Фурье заңын қолданамыз. Жылуөткізгіштік теңдеуін энергияның сақталу заңының теңдеуімен, Фурье теңдеуінен тұратын жүйенің математикалық эквиваленті ретінде қарастырамыз.  (1.7)Энергияның сақталу заңының теңдеуін қолданамыз. Бұл жағдайда жүйенің массалар центрінің өзгерісі жоқ деп, яғни w=0 деп қарастырамыз. Бұл жағдайда (1.7) теңдеу ықшамдалады, келесі түрге келеді:  (1.8)Тек жылуөткізгіштік процесін қарастырғанда оң жақтағы соңғы мүшесін терең қарастырамыз, тек қандай да бір энергияның (немесе жылудың) бөлінуі маңызды.  (1.9) белгілейміз.Жүйенің ішкі энергиясы u тек оның температурасына тәуелді деп есептейміз. Идеал осылайша, жылусыйымдылық деп сол сыртқы параметрлерде жүйенің ие болатын жылу сыйымдылығын аламыз. Осылайша,  (1.10)Мұндағы  -сыртқы параметрлердің белгілі бір мәніндегі жылусыйымдылық. Егер (1.8) теңдеудегі жылу ағынын (3) теңдеуге сәйкес өрнектесек және (9,1) теңдеулерді қолдансақ, келесіні аламыз:  (1.11)(1.11) теңдеу жылуөткізгіштік теңдеуінің неғұрлым жалпы математикалық жазбасы. Жалпы жағдайда 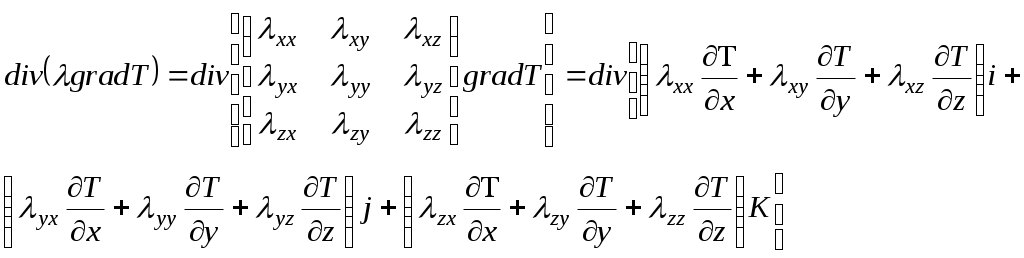жылуөткізгіштік коэффициенті тензор, және осылайша оң жақтағы бірінші мүше тензорды векторға көбейту ережесіне сәйкес келесідей жазылады. (1.12) өрнек келесідей жеке жағдайлар ықшамдалады: 1. Қарастырылатын жүйе изотропты, және осылайша жылуөткізгіштік тензоры скаляр. Онда  (1.11) өрнек келесідей түрге келеді: (1.12)мұндағы  - Лаплас операторы, ал (1.13)Жылуөткізгіштік коэффициенті координаталарға, ал тығыздық пен жылусыйымдылық уақытқа тәуелсіз десек, жылуөткізгіштік теңдеуі келесі түрге келеді:  (1.14)мұндағы  - Максвелл бойынша жылуөткізгіштік коэффициенті немесе Кельвин бойынша жылу диффузиясының коэффициенті:  . Стационар процестер үшін жылуөткізгіштік теңдеуі Пуассонның әдеттегі теңдеуіне келеді:  .Ішкі жылу көздері болмаса, (1.14) теңдеу Лаплас теңдеулеріне келеді:  2. Жылуөткізгіштік тензорының компонентері координаталарға тәуелсіз. Магнит өрісі жоқ. Бұл жағдайда (12) өрнек келесідей түрленеді: (1.15) 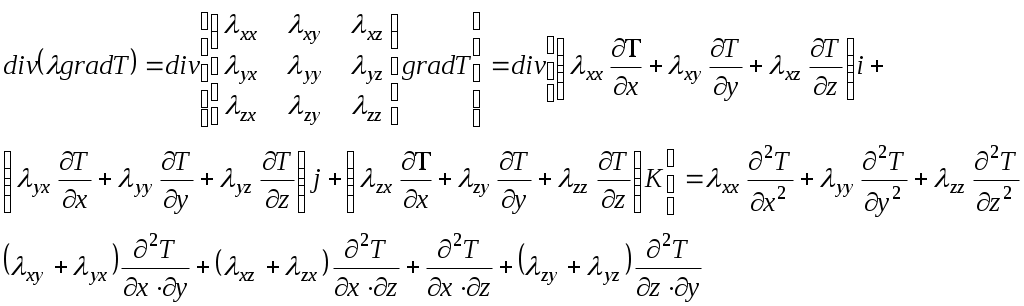 Екінші ретті дифференциал теңдеулердің теориясында көрсетілгендей, өрнектің оң жағына координаталарды ауыстыру арқылы аралас туындыларды жойып, келесі түрге келтіруге болады:  (1.16)мұндағы  - жаңа төртбұрышты координаталар. Алынған жағдай үшін жылуөткізгіштік теңдеуі келесідей жазылады:  (1.17)енгізілген жаңа координаталар ( ) жүйесін бас жүйе, ал оның остерін жылуөткізгіштіктің негізгі остері деп атаймыз. (1.17) теңдеуді тағы да ықшамдаймыз, ол үшін координатаны тағы да түрлендіреміз: (1.18)Мұнда шамалары кездейсоқ таңдалып алынды. 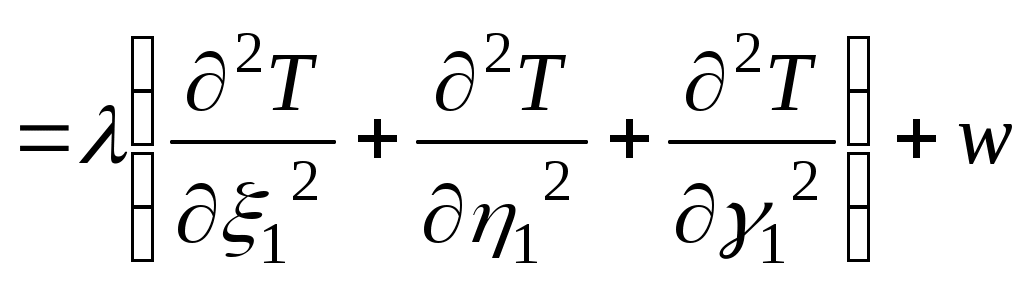Жаңа координаталарда (17) теңдеу келесідей жазылады:  (1.19)1.2.Шекаралық және бастапқы шарттары Жылуөткізгіштің дифференциалдық теңдеудің жалпы жағдайда көп шешімдері болады. Бұл жиының ішінен нақты қарастырылған процессті бірмәнді сипаттайтын жауапты алу үшін негізгі теңдеуге қосымша шарттарды қосу керек. Бұл шартта тікелей экспериментпен анықталады, немесе эксперимент мәліметтерін жалпылау арқылы табылады. Дифференциал теңдеудің шешімі деп, теңдеуді тепе-теңдікке жалпылайтын және осы қосымша шарттарды қанағаттандыратын  функциясын аламыз. Шешімнің графигі төртөлшемді кеңістіктегі қандайда бір бет болып табылады (интегралдық бет). Мұндай интеграциялауда қарапайым шекаралық шарттар  уақыт жазықтығы мен x,y,z координаталық беттермен жазықтықтың қиылысқандығы  функциясын беру болып табылады. Соңғылары, бастапқы шарттар, алғашқылары шекаралық шарттар деп аталады. Себебі, олар бастапқы  уақыт мезетінде жүйенің күйін көрсетеді. Екі кеңістік және координаталармен сипатталатын үшөлшемді облыс келтірілген. Жазықтықта бастапқы шарттар  деп, ал шекаралық шарттар -  жазықтықтарда беріледі. Фиксирленген уақыт мезетінде ( жазықтығы) температуралар өрісі температуралардың  шек . шекаралық мәндерін қоса алғанда  изотермелар жиынымен беріледі. Кеңістік уақыттың облысқа тән t функциясының үзіліссіздік шарты, сонымен бірге оның туындыларының (біріншісі бойынша, екіншісі және біріншісі x,y,z бойынша) шекті жағдайлар үшін орындалмайды. Шектелген кеңістік облыстарға берілген есептерден басқа, шекті немесе жартылай t шекті облыстар үшін есептер бар. Соңғысына іс-тәжірибеге көптеген маңызды есептер енеді (жылудың жұқа пластинкада таралуы, жылудың ұзын жұқа пластинкада таралуы).Бастапқы және шекаралық шарттардың негізгі типтерін қарастырамыз. Бастапқы шарттар. Дифференциалды жылуөткізгішті теңдеу - айнымалысы бар бірінші ретті теңдеу болатындықтан, бастапқы уақыт мезетінде келесідей функцияны беру жеткілікті: (1.20) - үздіксіз немесе үзлісті берілуі мүмкін. Егер үзіліссіз болса, онда негізгі дифференциал теңдеудің төмендегі шартты қанағаттандыратын t төмендегідей шешім аламыз.  (1.21)Егер функциясының бастапқы таралуы үзілісті болса, онда аз уақыт аралығынан кейін үзіліс жерлерінде температураның теңдесуі жүреді және t шешім (25,2) шартты қанағаттандыруы керек.Практикада қарапайым бастапқы шартты есептер кездеседі:  (1.22)жеке алғанда осы жағдайға орныққан режимнен шығуының бастапқы шарттары (“суық” күйден қыздыру, стационар режимдегі жұмыстан кейінгі суыту және т.б) келеді. Бұл жағдайда теңдеуді шешу айтарлықтай жеңілдейді. Бастапқы шарттарды елемейтін шекті жағдайлар да кездеседі. Мысал ретінде стерженнің ішінде жылудың таралуын қарастырамыз. Егер уақыттың есептік мезеті жеткілікті дәрежеде бастапқыдан алыс болса, онда температуралық өріс іс жүзінде тек шекаралық шарттармен – бастапқы шарттардың ықпалы уақытпен бірге бәсеңдейді. Осылайша , тәжірибе шексіз ұзаққа созылады және бастапқы шарттар керексіз. Осы жағдайда шекарадағы температураның периодты тербелісі келеді, ұзақ уақыт өткен кезде жүйенің нүктелер температурасы шекарадағы температураның тербеліс жиілігіне сәйкес келетін жиілікті заңмен өзгереді. Бастапқы таралуды дәл ескергенде периодты шешім болмайды, әйткенмен, практикаға қажетті дәлдікпен бұл қателіктің ықпалын ескермеуге болады. Жалпылай айтқанда, кез-келген пішінді денелер үшін бастапқы шарттар тек стационар процесстің бастапқы кезеңі кезеңінде ғана ықпал етеді. Қандай да бір  мезетінен бастап, регуляры деп аталған денедегі температураның таралуы бастапқы шарттарға тәуелсіз тек шекаралық шарттармен анықталатын режим орнайды. Шекаралық шарттар Кейбір типтік шекаралық шарттарды қарастырамыз. а) Бетте  түріндегі функциямен анықталатын температура берілген. Функция қандайда бір  уақыт аралығында берілген, мұндағы  - процесс зерттелетін қандайда бір уақыт аралығы. Облыстың ішінде негізгі теңдеуді қанағаттандыратын және шекарада  берілген мәнін қабылдайтын  функциясын табу керек болсын. Математикалық физикада бұл есеп бірінші шекті есеп деп,ал Лаплас теңдеуі жағдайында  -Дрихле есебі деп аталады. Кейбір жағдайда “бірінші ретті шекаралық шарттар” деп аталады. Бірінші ретті шекаралық шарттарға шекарадағы температураның берілген өзгеруі кезіндегі жүйенің қыздырылуының және сууы жағдайындағы немесе беттегі жылу интенсивті алмасқан кезіндегі есептер жатқызылады. Бірінші ретті шекаралық шарттар практикада өте сирек кездеседі, себебі беттің температурасы ізделінді шама болады. Әйткенімен, шектелген асқан интенсивті (мысалы, қайнау, куонденсация, сұйық металдардың мәжбүр тербелісі), жұмыстық ортаның tор температурасы tбет беттің температурасына жуықтап тең болатын процесстер кездеседі. Бұл температуралардың айырымы Iq жылу ағыны және зетттеу мәселесі конвективті жылу алмасу мен фазалық түрленудегі жылу алмасу процесстеріне қарасты болатын  жылу берілу коэффициентерімен анықталады.  болғанда tор tбет. Мысал ретінде, “жылу соққысы” деп аталатын құбылысты қарастырамыз. Мысал ретінде “жылулық соққы” деп аталатын құбылысты қарастырамыз. Суық қабырғаға температурасы  . Қабырғаға соқтығысып бу конденсацияланады  және беттің температурасы тез ортаның температурасына жуықтайды. Бұдан ары ортаның температурасын тұрақты ұстағанда қабырғаның қызуы іске асады. бұл жағдайда қалыңдығы r қабырғадағы температураны есептеу І ретті шекаралық шарттарды қолдану арқылы болуы мүмкін. Температураның шеттік  таралуы стационар күйге сәйкес келеді. Қарастырылған шекаралық шарттар практикада өте сирек орындалады: ережеге сәйкес нақты денелердің бетінде температуралық өрісті бұрмалайтын контактілік жамылғылар болады.б) Шекарада жылу ағыны берілген (екінші шекаралық есеп, ІІ реттті шекаралық шарттар).  (1.23)теңдеуді бұл жағдайда шешу облыстың ішінде негізгі теңдеуді қанағаттандыратын қалыпты туындысы шекарада  (1.24)Лаплас теңдеуі үшін Нейман есебі деп аталады. в) Шекарада туынды мен функцияның арасында сызықтық қатынас берілген (үшінші шектік есеп, үшінші текті шекаралық шарттар);  1.(25)Бұл шекаралық шарт температурасы берілген ортамен жылу алмасуына сәйкес келеді коэффициенті ортаның қабырғамен жылулық әсерлесуінің интенсивтілігін сипаттайды.Лаплас теңдеуі үшін есеп келесідей жазылады:  бұл аралас есеп деп аталады:  Дирихле есебі, Нейман есебі.(2) шекаралық шартты өлшемсіз түрге келтіреміз   мұндағы   - тек өлшем, -қандайда бір фиксирленген температура.Ві (Био) критериі ұқсастық теориясында кеңінен қолданылады. Ві  болғанда үшінші текті шарт бірінші текті шартқа ауысады (үлкен интенсивтегі жылу алмасады қабырғаның тепературасы тең) және бұл жағдай неғұрлым әмбебап болып табылады. Ві=0 жағдайы шекарасында жылулық изоляциясы бар есепке келеді. Үшінші текті шекаралық шарттар практикада кеңінен қолданылады. (шекарадағы конвективті жылу алмасу) Орта біртекті емес және  коэффициентері үздікті функциялар болып табылады (төртінші текті шартты шекаралық шартты көп қабатты жүйе. Әрбір қабатың ішінде  () ізделінді функциясы жылуөткізгіштік теңдеуін өзінің коэффициенттерімен ал қабаттардың шекарасында түйіндесу шарттарын қанағаттандырады.)Қарапайым жағдайда - қабаттар арасында идеал контакт болғанда, түйіндесу шарты температураның үздіксіздігімен жылу ағынының үздіксіздігіне негізделеді:  Қалың қабаттардан басқа нақты (реал) денелерде қабаттар арасындағы жылу берілу контактілік жылу алмасу арқылы іске асады (сәуле шығарудың, жылуөткізгіштіктің, конвекцияның күрделі процестері). Контактілік жылу алмасуда шекаралық шартттарда дәл бере алмаймыз және есептеулер үшін жуық шешімдерді қолданады. Жоғарғы энергиялы физиканың дамуымен бірге төртінші шекаралық шартты есептер жанама мәнге ие болды – олар ракета басының көпқабатты жамылғысы, энергия түрлендіргіштер және т.б. д) Сызықты шекті есептерден басқа, шекаралық шарттары сызықты емес есептер де қарастырылады. Шекарада сәулелену заңы орындалатын, сәулелену арқылы жылу берілу есептері осыған жатады:  Мұндағы Е - беттің сәулелік қабілетін сипаттайтын қараю дәрежесі; - Стефан-Больцман тұрақтысы; Тор-зерттейтін объектіні қоршаған орта мен дененің температурасы.4 текті шекаралық шартта есептерді сыртқы сызықтық емес есептері деп атаймыз. Сәулелену арқылы жылутасымалдану жоғары температураларда жұмыс істейтін барлық жүйелерге тән, сондықтан сыртқы сызықты емес есептер көкейісті болып табылады. Әйткенмен, қазіргі уақытта бұл шекаралық шартты есептердің шешілгендерінің саны шектеулі, ал шешімнің ортақ әдістемесі жоқ. 1.3.Бетонның жылуөткізгіштік қасиеттері Бетонның ең маңызды сипаттамаларының бірі, әрине, оның жылу өткізгіштік болып табылады. материалды әр түрлі түрлері үшін осы параметрді өзгертіңіз кең ауқымында болуы мүмкін. Бетонның жылуөткізгіштігі, бәрінен бұрын оның толтырғышына байланысты. Ол пайдаланылатын толтырғыш түріне, бетон жылу өткізгіштігі, барлық байланысты материалдық жеңіл, ол суықтан жақсы изоляторы болып табылады.Түрлі материалдар ғимараттар мен құрылыстарды салу кезінде пайдаланылатын болады. Ресей климат жағдайында тұрғын үй және өндірістік ғимараттар, әдетте қымтау. олар арнайы изоляторларының құрылысын, үй-жайда жайлы температураны ұстап тұру үшін оның негізгі мақсаты пайдаланылады, бұл кезде, болып табылады. минералды мақтадан немесе көбік полистирол қажетті сомасын есептеген кезде міндетті жылу өткізгіштік базалық материал конверттерді құрылыс салу үшін пайдаланылады ескеру. Тарау бойынша қорытынды тұжырымдар Дербес туындысы теңдеулерді шешудің сандық әдістері теориясы айырым схемаларының теориясы деп аталатын математиканың күрделі және ауқымды бөлімін құрады. Осы жұмыста негізінен бұл әдістеменің ЭЕМ-де іске асырудың және құрудың практикалық сұрақтарына арналады. Есептеу техникасын және сандық әдістерді қолдану дәл және аналитикалық тәсілдерді қолдану мүмкін емес. Көп өлшемді, сызықты емес, стационар емес есептердің жылу алмасуының зерттелетін өрістік есептерінің топтарын айтарлықтай кеңейтеді. Нақты объектілердегі жылу алмасу процесін сипаттайтын математикалық моделдерді таңдағанда олардың рұхсат етілген күрделілік шекаралары қазіргі уақытта көбіне тек ЭЕМ-нің қорлары мен сандық тәсілдер мүмкіндіктерімен ғана емес, бұл модельдерге енетін кіріс ақпараттарының келешегімен де анықталады. Әртүрлі кеңістік- уақыттың өрістерді анықтағанда кеңістік айнымалыларының және уақыт интервалының берілген өзгеру облыстарындағы дербес туындылардың дифференциялдық теңдеулері үшін шекаралық есептердің шешімі табылды. Пайдаланылған әдебиеттер тізімі 1.Г.В. Кузнецов, М.А.Шеремет. Разностные методы решения задач теплопроводности. Томский политехнический университет, 2007 г 2. Сайболатов С.Ж., Құлбеков М.Қ. Кәдеге асқан қалдықтар. Алматы, “Білім” қоғамы, 1987. 3. Г.Н.Дульнев., В.Г.Парфенев., А.В.Сигалов. Применение ЭВМ для решения задач теплообмена. М., «Высшая школа».,1990, 206 стр. 4. Беляев Н.М., Рядоно А.А. Методы теории теплопроводности. Т.1,22.м.1982. 5. Бахлов Н.С. Численные методы.М.,1975. 6. И.Ф.Жеребятьев, А.Т.Лукьянов. Математическое моделирование уравнение типа теплопроводности. М.«Энергия», 1968. 7. Грим Р.Е. Минералогия и практическое использование глан. М.,Мир, 1967, с.511. 8. Патанкар С.Численные методы решения задач теплообмена и динамики жидкости. М.,1984. 9. Кравцов И.А. Изучение некоторых процессов тепла – и массообмена, связанных с физико-химическими превращениями в глинах при обреф. дис. На соиск.учен.степени канд.техн.наук. Киев, 1973. 10. Лыков А.В. Теория теплопроводности. М., Высшая школа, 1967, с.599. 11. Лыков А.В. Применение методов термодинамики необратимых процессов к использованию тепло – и массообмена. Инж.-физ. журнал., 1965, т.IX, Кингери У.Д. Введение в керамику. М., Госстройиздат., 1967, с.500. №36 с.287 12. Оцисик М.Сложный теплообмен.М.,1976. 13. Мучник Г.Ф., Рубашов И.В. Методы теории теплообмена. 1 часть. М.,”Высшая школа”. 284 стр. 14. Михеев М.А. Основы теплопередачи. Москва15. Исаченко В.П. Теплопередачи. Москва16. 15-ші ғылыми студенттік конференция « Жылуөткізгіштік теңдеулерін шешудің шекті – айырымдық әдісі». Тұрсынбаева Қ. Шымкент қ, 2012ж
|