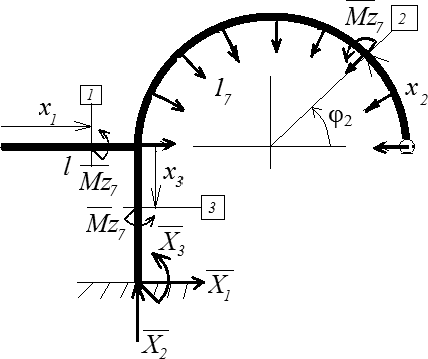расчет рамы методом сил. Имеет

Название	Имеет
Анкор	расчет рамы методом сил
Дата	24.05.2023
Размер	201.64 Kb.
Формат файла
Имя файла	Raschyot_staticheski_neopredelimoy_ramy_metodom_sil_-_KR (4) (1).docx
Тип	Документы #1156163
страница	2 из 5

1 2 3 4 5

^j dx

Mz_iMz



2

1
_lEJ_z

^j dx

Mz_iMz



3
_lEJ_z

^j dx

3

2
определение сразу позволяет сделать вывод, что податливости имеющие индексы неподвижных направлений тождественно равны 0.

Рис. 4. Вспомогательная система
Таким образом, система канонических УРП приобретает вид: ^δ44^X4^{+ δ}45^X5⁺^δ46^P6⁺^δ47^q7 ⁼^Δ4 ⁼⁰

^δ54^X4⁺^δ55^X5⁺^δ56^P6⁺^δ57^q7 ⁼^Δ5 ⁼⁰
По числу КП видно, что единичные силы необходимо будет прикладывать в 4, 5, 6 и 7 направлениях, т.е. потребуются четыре вспомогательные системы: 4-я, 5-я, 6-я и 7-я ВС. Результаты работы с этими ВС удобно свести ив таблицу 1.

Процедура вычисления КП предполагает определение значений внутренних сил в поперечных сечениях и интегрирование по длине всех стержневых элементов конструкции в виде

т.е. в виде трёх интегралов для каждого участка.

7ВС.
Уравнения равновесия ^X1 ⁼⁰

^X2 ^-⁽¹7^*2l)^{= 0}

^X3 ^–^P*l^–⁽¹7^*2l)^*l⁼⁰
^По^x1^:^Mz7 ^{= 0}

^{По x}2^{: Mz}7 ^{– 1}7^{* l2*(1 - cos(x}2^{/l)) = 0}^{По x}3^{: Mz}7 ^–⁽¹7^*^2l)*l⁼⁰

Построение эпюр изгибающих моментов

На каждом участке обозначено поперечное сечение с соответствующим номером, направлением движения x и внутренний изгибающий момент Mz, на оси которого будут записываться уравнения равновесия для выделенной (отсечённой) координатой x части участка. В правой колонке таблицы 1. выписаны уравнения равновесия и соответствующие выражения для Mz.

Таблица 1.
В данном случае при определении значений Mz участки были выбраны так, что отпала необходимость в определении значений реакций опоры. Полученные выражения Mz переносятся в таблицу 2.

	4ВС. Уравнения равновесия ^X1 ⁺¹4 ⁼⁰ ^X2 ^{= 0} ^X3 ^–¹4^{* l}^{= 0} ^{По x}1^:^Mz4 ^{= 0} ^{По x}2^{: Mz}4 ^{+ 1}4^{* lsin(x}2^{/l) = 0}^{По x}3^:^Mz4 ^–¹4^^x3 ^{= 0}
	5ВС. Уравнения равновесия ^X1 ⁼⁰ ^X2 ^{+ 1}5 ^{= 0}^X3 ⁺¹5^2l⁼⁰ ^По^x1^:^Mz5 ^{= 0} ^{По x}2^{: Mz}5 ^{+ 1}5^{ l(1 - cos(x}2^{/l)) = 0}^{По x}3^:^Mz5 ^{+ 1}5^^2l^{= 0}
	6ВС. Уравнения равновесия ^X1 ⁼⁰ ^X2 ^{+ 1}6 ^{= 0}^X3 ^–¹6^l⁼⁰ ^{По x}1^:^Mz6 ^–¹6^^x1 ^{= 0}^{По x}2^:^Mz6 ⁼⁰ ^По^x3^:^Mz6 ^–¹6^*^{l =}⁰

Таблица 2.

Интервал значений аргумента	^Mz4	^Mz5	^Mz6	^Mz7
^{0 ≤}^x1 ^≤^l	0	0	^x1	0
^{0 ≤}^x2 ^≤^πl	^-^l^*sin(x2^/l)	^-^l^(1-cos(x2^/l))	0	^-^l2^(1-cos(x2^/^l⁾⁾
^{0 ≤}^x3 ^≤^l	^x3	-2l	l	2l²

Запишем выражения для всех необходимых КП:

_^lMzMz

^^lMzMz

1 2 3 4 5